钢轨内自感的计算及影响因素分析

朱　峰，李朋真，李嘉成，李　鑫，沈　迪

(1.西南交通大学 电气工程学院，四川 成都　610031；2.长春轨道客车股份有限公司，吉林 长春　130062)

钢轨是电气化铁路牵引电流和轨道信号电流的通道[1]，当列车在轨道上行走时，钢轨内自感使得部分牵引电流，特别是牵引电流当中的谐波，通过车体进行回流，如果此时车体的接地保护布局不合理，会在车体上形成车体对钢轨的较高电势差，容易对转向架上的电气设备造成干扰或损伤[2-4]。另一方面，当2根钢轨中牵引电流分配不平衡时，扼流变压器初级产生的磁通就抵消不掉，磁通差值在信号侧(扼流变压器二次侧)产生感应电压，有可能使信号设备产生干扰甚至误动；而钢轨内自感可用于确定钢轨中的牵引电流分布，分析轨道中不平衡电流及对列车传感器等敏感设备的干扰[5-6]，因此确定钢轨内自感的值对于高速列车的安全运行具有重要的意义。

目前，国外对于钢轨内自感的研究主要是通过软件仿真[7]以及实测的方法[8-11]确定不同操作环境和不同型号钢轨的内自感；国内是在研究轨道电路特性时给出了钢轨内自感的测量数据[12-13]，但是还没有文献分析钢轨内自感的特性。因此，有必要从钢轨内自感的本质着手，对牵引电流和钢轨等效半径如何影响钢轨内自感进行深入研究。

本文根据电流与磁链相互作用的机理，充分考虑牵引电流密度沿径向相位变化对钢轨内自感的影响，推导用级数表示的钢轨内自感解析公式；研究钢轨内自感与牵引电流密度相位、牵引电流、牵引电流频率和钢轨等效半径的关系，并从物理底层剖析这4个因素对钢轨内自感的影响规律，为解决高速列车设备和信号系统的电磁干扰提供理论支撑。

1　理论分析

1.1　电流与磁链相互作用机理的分析

因为能量不能通过钢轨内部的电磁场进行传输，而钢轨内部的功率主要为焦耳热损耗功率和用于建立电磁场的无功功率，因此钢轨单位长度体积内的无功功率Q为

(1)

式中：j为虚数单位；ω为电流角频率；B为磁感应强度；H*为磁场强度共轭复数；dV为导体的体积微元；Ψ为磁链；I为钢轨中的牵引电流，V为钢轨单位长度体积。

由于式(1)是通过场量体现能量关系的，为便于分析，将场量用电流密度来表示。首先将磁感应强度B用向量磁位A表示，即B=▽×A，其中▽为拉普拉斯算子；再运用关于向量a，b的恒等式▽·(a×b)=b·(▽×a)-a·(▽×b)将式(1)改写为

(2)

再根据高斯定理有

(3)

式中：dS′为无穷远处面元。

由于H*在无限远处以距离平方的倒数趋于零，A在无限远处以距离的倒数趋于零，而无限远处的球面是以距离的平方趋于无穷大，故式(3)等号后面的项∮(A×H*)·dS′=0，则式(2)可改写为

(4)

式中：S为钢轨截面，dl为电路闭合线路的长度微元；J*为磁感应强度为B的磁力线包围区域内电流密度的共轭复数；dS为钢轨截面微元。

再应用斯托克斯定理有

∮A·dl=∬B·dS

(5)

将式(5)代入式(4)并化简可得

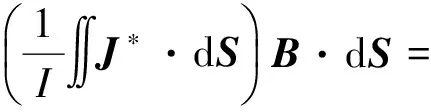
(6)

式中：I′*为面积微元dS中流过的交链电流的共轭复数。

1.2　钢轨内自感的计算公式推导

由式(6)可知：交链电流的共轭复数I′*和磁感应强度B是计算磁链的重要参数，而I′*和B均由钢轨中牵引电流密度的分布决定，故应首先分析钢轨中牵引电流密度分布规律。当钢轨中的牵引电流为正弦时变电磁场时，可将其看成磁准静态场(MQS)，因此，忽略位移电流，利用涡流方程求解钢轨中牵引电流密度的分布规律，即

(7)

其中，μ=μrμ0

式中：J为钢轨内任一点的牵引电流密度；γ为钢轨电导率；μ为钢轨磁导率；μ0为真空磁导率；μr为相对磁导率；t为时间。

由于钢轨截面为工字形，利用式(7)直接计算牵引电流密度J比较困难；又因为集肤效应使得牵引电流主要集中于钢轨表面。所以，为了简化运算，将钢轨等效为周长不变的实心圆柱体[14]，如图1所示。图中：R为钢轨的等效半径；ρ为钢轨等效圆柱体内的任意等效半径，ρ≤R。

图1　等效后的钢轨模型

设任意等效半径ρ处的牵引电流密度为J(ρ)，将式(7)中直角坐标系下的涡流方程改写为柱坐标系下的涡流方程，即

(8)

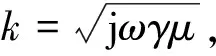
J(ρ)=[c1J0(kρ)+c2Y0(kρ)]ez

(9)

式中：J0为0阶第一类贝塞尔函数；Y0为0阶第二类贝塞尔函数；c1，c2为系数；ez为沿z轴正方向的单位向量。

又因为ρ→0， Y0(kρ)→∞， 应取c2=0，而且

(10)

因此可得任意等效半径ρ处的牵引电流密度为

(11)

其中，

式中：J1为1阶第一类贝塞尔函数。

牵引电流密度的相位θ为

(12)

式中：Im()为虚部值；Re()为实部值。

式(11)和式(12)表明：钢轨中牵引电流密度在衰减的过程中还伴随有相位的变化，并且由于相位不同，计算交链电流时，部分电流相互抵消，因此，应考虑相位对交链电流的影响。在任意半径为ρ的等效圆内交链的有效电流I′为

(13)

式中：ρ′为在半径为ρ的圆内任意点到钢轨等效圆圆心的距离； dρ′为在ρ′处径向距离微元。

由于任意半径ρ上任一点磁场强度的大小相等，根据安培环路定理可得磁感应强度为

(14)

式中：eφ为钢轨内半径为ρ处沿切向的单位向量。

式(14)中，对车载电子装置而言，电磁波的波长远大于3 km，因此，在实际计算中，磁感应强度B沿轴向相位的变化可以忽略不计；又因为单位长度钢轨内存在dS=dρeφ，故将式(14)代入式(6)得

(15)

钢轨内自感为

(16)

将J1用级数表示，即

(17)

将式(17)代入式(13)，并结合式(16)可得单位长度钢轨的内自感为

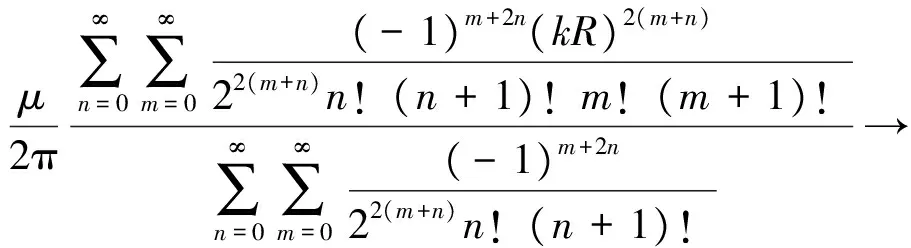
(18)

由式(18)可知：钢轨内自感L与钢轨磁导率μ成正比关系，与钢轨的传播常数k和钢轨等效半径R存在幂指数关联。又因为：

(1)在式(7)中，定义的钢轨内任一点的电流密度J为向量，即包含了牵引电流密度相位θ；

(2)钢轨相对磁导率μ在大牵引电流条件下也呈现非线性变化，即相对磁导率μr由牵引电流I决定；并且文献[15—16]通过实验给出了相对磁导率随牵引电流的变化曲线；

(4)钢轨电导率γ受其他因素影响较小，即其为定值，取值γ=4.44×103S·mm-1时满足工程的需要[17]。

所以，钢轨内自感L与牵引电流密度相位θ、牵引电流I、牵引电流频率f和钢轨等效半径R这4个因素成非线性关系。

2　钢轨内自感影响因素的分析

基本参数取值为：I=200 A，μr=220，γ=4.44×107S·m-1，f=50 Hz，R=0.109 1 m。

2.1　电流密度相位θ与钢轨内自感L的关系

按基本参数进行取值，根据式(12)计算得到钢轨沿径向各点的电流密度相位变化特性，如图2所示；根据式(13)计算电流密度相位对任意等效半径为ρ的等效圆内交链电流的影响程度，如图3所示。

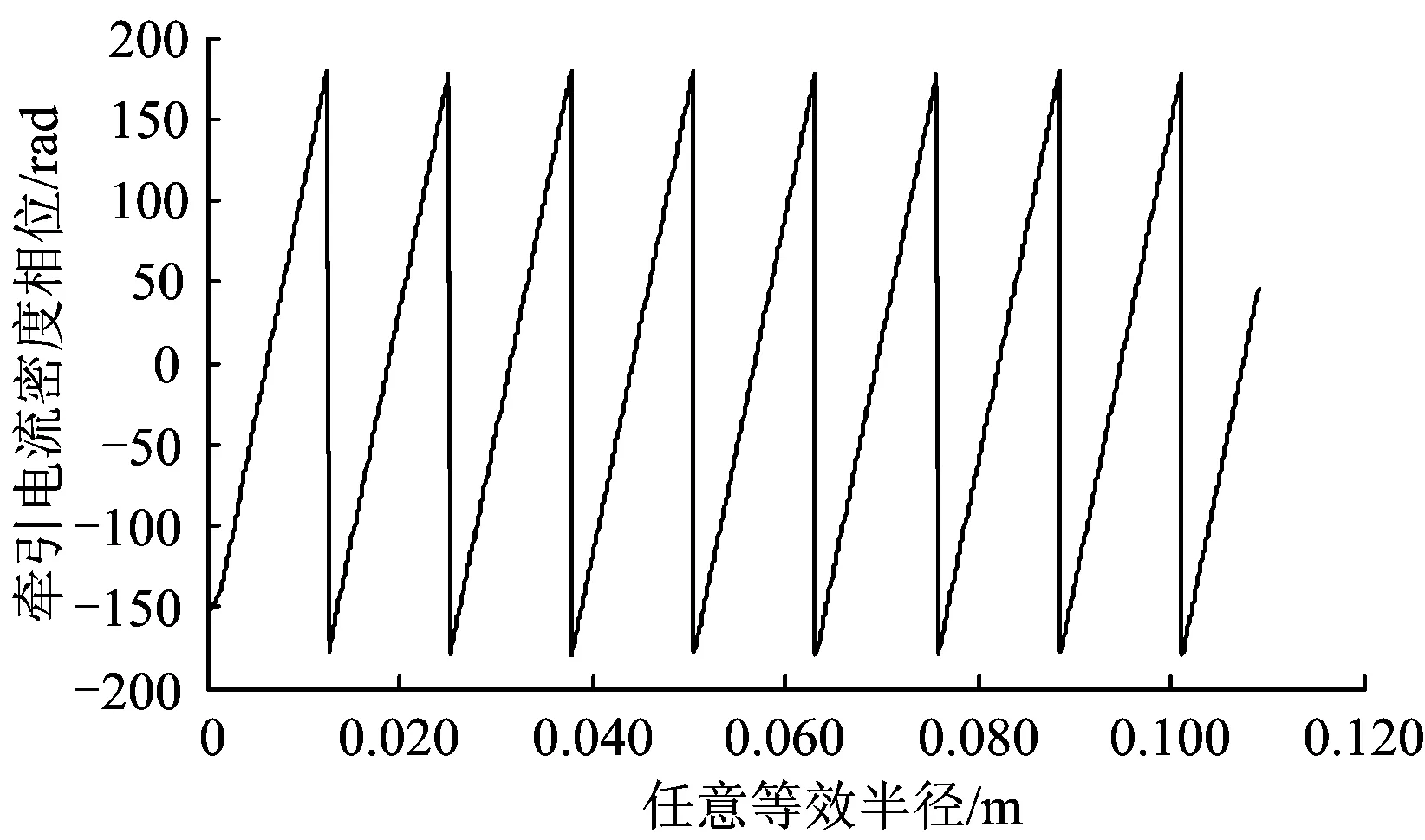
图2　钢轨沿径向各点的牵引电流密度相位

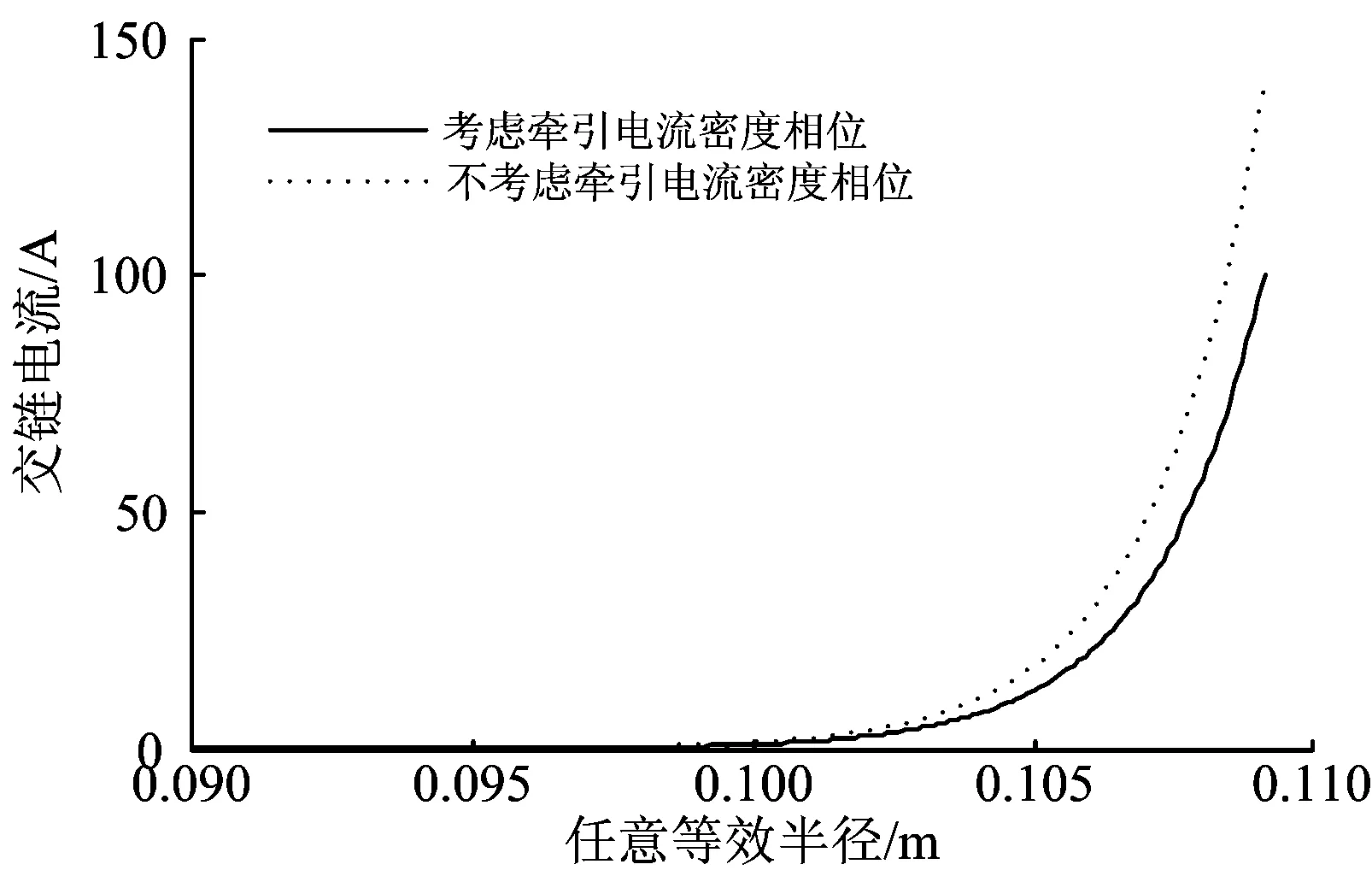
图3　牵引电流密度相位对交链电流的影响

由图2可知：同一时刻同一截面内，钢轨中电流的流向是不同的。由图3可知：当R=0.109 1 m时，若考虑相位，则交链电流I′=100 A，而不考虑相位，则交链电流I′=141 A，可见，不考虑相位时得到的交链电流比考虑相位时要大41%；这是因为，若相位不同，电流密度叠加时，部分交链电流可以相互抵消。因此，必须考虑电流密度相位对钢轨内自感的影响。

2.2　钢轨内自感与牵引电流的关系

牵引电流I取50，100，150，…，1 150 A，相对磁导率按照文献[15，16]给出的牵引电流与磁导率的关系曲线取值，根据式(18)计算得到不同牵引电流I时的钢轨内自感L，如图4所示。为了对比分析本计算结果的合理性，将文献[7]关于60 kg钢轨的不同牵引电流I时的内自感仿真值，文献[8]关于60 kg钢轨的不同牵引电流I时的内自感实测值也列于图4中。

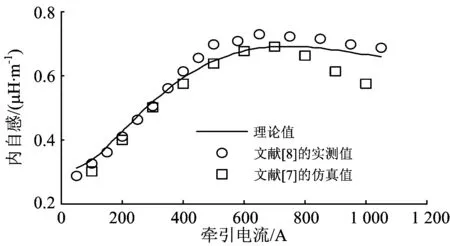
图4　钢轨内自感与牵引电流的关系

由图4可知：当牵引电流小于680 A时，钢轨内自感随着牵引电流的增大而增大；当牵引电流大于680 A时，钢轨内自感随着牵引电流的增大而略有减小。这是因为：当牵引电流小于680 A时，磁通没有达到饱和，磁导率随着牵引电流的增大而增大[15-16]，由式(18)可知，内自感L与磁导率μ和传播常数k都有关系；一方面，传播常数k随着磁导率μ增加而增加，由式(11)可知，传播常数k增加，牵引电流I更集中于钢轨表面，在任意等效半径为ρ的圆内，交链电流I′增大的倍数小于牵引电流I增大的倍数，钢轨内自感L有减小的趋势；另一方面，随着磁导率μ的增加，钢轨内自感L有增大的趋势；又因为磁导率μ的增加使得钢轨内自感L增大的速率大于k增加使得钢轨内自感L减小的速率，所以钢轨内自感L随着牵引电流的增大而增大。当牵引电流大于680 A时，磁通达到饱和，磁导率随着牵引电流的增加而略有减小，同理可知，钢轨内自感L随着牵引电流的增大而减小。

2.3　钢轨内自感与牵引电流频率的关系

牵引电流频率f取50，100，150，…，1 000 Hz，为了与文献[18，19]对比，以115lb钢轨为例，其等效半径R=0.102 1 m，其余参数按基本参数取值，根据式(18)计算不同牵引电流频率f时的钢轨内自感L，并将文献[18，19]给出的不同牵引电流频率f时钢轨内自感的测量值也列于图5中。

图5　钢轨内自感与牵引电流频率的关系

由图5可知：钢轨内自感随着牵引电流频率的增大而减小。这是因为：当牵引电流频率f增大时，传播常数k增大，由式(11)可知，牵引电流I更集中于钢轨表面，在任意半径为ρ的圆内，交链电流I′减小，由式(15)可知磁链Ψ也减小，因此钢轨内自感L随着牵引电流频率f的增大而减小。

2.4　钢轨内自感与钢轨等效半径的关系

钢轨等效半径R取0.109 1 m(P60)，0.096 6 m(P50)，0.088 9 m(P43)；牵引电流频率f取50，100，150，…，1 000 Hz；其余参数按基本参数取值；根据式(18)计算不同钢轨等效半径、不同牵引电流频率f时的钢轨内自感L，如图6所示。

图6　钢轨等效半径对钢轨内自感的影响

由图6可知：钢轨内自感随着钢轨等效半径的增大而减小。这是因为电流主要集中于钢轨表面，当钢轨等效半径增大时，钢轨截面的面积增大，任意等效半径ρ内包围的交链电流I′减小，又因为牵引电流I和磁导率μ不变，由式(15)可知磁链Ψ减小，所以钢轨内自感逐渐减小。

3　结　论

(1)同一时刻同一截面内，钢轨中牵引电流的流向是不同的。不考虑相位时得到的交链电流比考虑相位时要大41%；这是因为，若相位不同，电流密度叠加时，部分交链电流可以相互抵消。因此，必须考虑牵引电流密度相位对钢轨内自感的影响。

(2)当钢轨磁通没有达到饱和时，钢轨内自感随着牵引电流的增大而增大；当磁通达到饱和时，钢轨内自感随着牵引电流的增大而略有减小。

(3)钢轨内自感随着牵引电流频率的增大而减小。这是因为，牵引电流频率增加，由于集肤效应，电流更集中于钢轨表面，同等长度半径ρ内包围的交链电流减小，总磁链就减小，从而使得钢轨内自感减小。

(4)钢轨内自感随着钢轨等效半径的增加而减小。这是因为，牵引电流主要集中于钢轨表面，钢轨等效半径越大，钢轨截面的面积越大，任意等效半径ρ内包围的交链电流I′减小，总磁链减小，从而使得钢轨内自感减小。

[1]张银花,周清跃,陈朝阳,等. 重载铁路高强钢轨的试验研究[J]. 中国铁道科学,2010,31(4):20-26.

(ZHANG Yinhua, ZHOU Qingyue, CHEN Zhaoyang，et al. Test Study on the High Strength Rails of Heavy Haul Railway[J]. China Railway Science，2010，31(4):20-26. in Chinese)

[2]袁德强, 张宇. CRH380B 型动车组保护接地改进方案[J]. 铁道车辆, 2014, 52(3): 19-20.

(YUAN Deqiang, ZHANG Yu. Improvement Scheme of Protection Grounding for CRH380B Multiple Units[J]. Rolling Stock, 2014, 52(3): 19-20. in Chinese)

[3]FILIPPONE F, MARISCOTTI A, POZZOBON P. The Internal Impedance of Traction Rails for DC Railways in the 1～100 kHz Frequency Range[J]. IEEE Transactions on Instrumentation and Measurement, 2006, 55(5):1616-1619.

[4]周利军，高强，黄军玲，等. 高速铁路27.5 kV电缆金属护层的雷击感应电压[J]. 中国铁道科学，2015，36(4):87-92.

(ZHOU Lijun，GAO Qiang，HUANG Junling，et al. Lightning Induced Voltage in the Metal Sheath of 27.5 kV Cable for High Speed Railway[J].China Railway Science,2015，36(4):87-92. in Chinese)

[5]熊卫东, 周清跃. 钢轨钢的纯净性与高纯净钢轨的发展[J]. 中国铁道科学, 2000, 21(4): 78-84.

(XIONG Weidong, ZHOU Qingyue. The Purity of Rail Steels and the Development of High-Pure Rails [J]. China Railway Science, 2000, 21(4): 78-84. in Chinese)

[6]毕红军, 吴运熙，潘行谦. 轨道不平衡电流模拟系统[J]. 北方交通大学学报, 1994, 18(2): 259-264.

(BI Hongjun, WU Yunxi，PAN Xingqian. Simulation of Conductive Interference on Electrified Railway[J]. Journal of Beijing Jiaotong University，1994, 18(2): 259-264. in Chinese)

[7]DOLARA A, LEVA S. Calculation of Rail Internal Impedance by Using Finite Elements Methods and Complex Magnetic Permeability[J]. International Journal of Vehicular Technology, 2009,2009: 1-10.

[8]MARISCOTTI A, POZZOBON P. Resistance and Internal Inductance of Traction Rails at Power Frequency: a Survey[J]. Vehicular Technology of IEEE Transactions, 2004, 53(4): 1069-1075.

[10]MARISCOTTI A, POZZOBON P. Measurement of the Internal Impedance of Traction Rails at 50 Hz[J].IEEE Transactions on Instrumentation and Measurement, 2000, 49(2):294-299.

[11]MARISCOTTI A, POZZOBON P. Measurement of the Internal Impedance of Traction Rails at Audio Frequency[J]. IEEE Transactions on Instrumentation and Measurement, 2004, 53(3):792-797.

[12]侯震宇. 无绝缘轨道电路对无砟轨道的适应性分析[D]. 成都：西南交通大学, 2009:312-317.

(HOU Zhenyu.Analysis of the Adaptability of Jointless Track Circuit to Ballastless Track[D]. Chengdu：Southwest Jiaotong University，2009:312-317.in Chinese)

[13]禹志阳, 杨奎芳, 申凤鸣. 轨道电路在无砟轨道条件下传输特性的研究[J]. 铁道学报, 2007, 29(5): 122-126.

(YU Zhiyang, YANG Kuifang, SHEN Fengming. Study on Transmission Performance of Ballastless Track Circuits[J]. Journal of the China Railway Society, 2007, 29(5): 122-126. in Chinese)

[14]WANG Y J, TSAI Y L. Calculation of the Frequency-Dependent Impedance of Rail Tracks Using a Four-Parameter Equivalent Tubular Conductor Model[J]. IEEE Transactions on Power Delivery, 2004, 19(3): 1142-1147.

[15]HILL R J, BRILLANTE S, DE Souza CR, et al. Electrical Material Data for Railway Track Transmission Line Parameter Studies[J]. IEE Proceedings-Electric Power Applications, 1999, 146(1):60-68.

[16]HILL R J，CARPENTER D C. Determination of Rail Internal Impedance for Electric Railway Traction System Simulation[J]. IEE Proceedings B Electric Power Applications,1991, 138(6): 311-321.

[17]SUN Y, NIU D, SUN J. Temperature and Carbon Content Dependence of Electrical Resistivity of Carbon Steel[J]. 2009 4th IEEE Conference on Industrial Electronics and Applications,2009:368-372.

[18]BROWN J C, ALLAN J. Calculation and Measurement of Rail Impedance Applicable to Remote Short Circuit Fault Currents[J]. IEE Proceedings B Electric Power Applications,1993, 140(6):417-420.

[19]HOLMSTROM F R. The Model of Conductive Interference in Rapid Transit Signaling Systems[J]. IEEE Transactions on Industry Applications, 1986, IA-22(4):756-762.