励磁作用下铁磁管道缺陷磁特性仿真

张丽攀 马冰洋 宋 凯 王 振

1.南昌航空大学无损检测技术教育部重点实验室，南昌，330063 2.南昌航空大学科技学院，南昌，330063

0 引言

管道，特别是铁质管道，作为存储运送石油、天然气等介质的重要载体，被广泛应用于油气开采、化工、城市地下管廊等基础建设方面，在国民生活以及工业生产中起着重要作用。根据相关标

?准，其出厂前必须进行100%检测［1］。涡流检测是一种普遍使用的检测方法。铁磁性材料在加工以及运输过程中由于外界因素导致材料表面或近表面产生不均匀的磁导率会干扰涡流检测的正常实施，因此对于铁磁性管道的检测，通常需要另外附加磁饱和装置［2］，以降低材料磁导率波动对涡流信号的干扰。国内外文献对铁磁材料磁饱和程度并没有明确定义，磁化后铁磁材料缺陷附近磁导率是否均匀一致也未有涉及，因此研究磁化后铁磁材料磁导率的分布状况对辨析磁化涡流检测的实质具有重要意义。

磁化涡流检测通常采用直流励磁或者永磁体磁化，目的均为降低检测区域的磁导率。多年来，国内外学者对该方法进行了许多研究［3⁃4］，对磁化条件下的铁磁材料电磁特性的研究大都集中在漏磁检测方面。熊龙辉等［5］研究了漏磁法检测钢轨裂纹时的巡检速度、励磁激励和磁轭提离距离对钢轨材料磁化强度的影响，并分析了其对检测灵敏度的影响。杨理践等［6］分析了漏磁信号幅值与工件厚度的关系，研究了钢板厚度对磁化效果的影响，指出了钢板磁饱和的临界点。对于铁磁材料的电磁检测研究，大多更关注检测技术本身的优化以及缺陷的磁场分布特性和磁化方法［7⁃10］，而对磁化状态下铁磁材料缺陷处的磁导率分布状况的研究尚不多见。

本文从仿真角度出发，以典型铁磁管道为对象，建立钢管数值计算的三维有限元模型，研究表面缺陷和内部缺陷附近的磁场以及材料磁导率的分布特征，以期得到缺陷磁导率与励磁强度的对应关系。

1 磁化仿真模型

铁磁管道的磁化过程与涡流检测是同时进行的，通常采用不含有铁氧体的穿过式线圈或者马蹄形线圈进行涡流检测，探头拾取的信号经过相敏检波及滤波过程后，仅有高频的涡流信号进入计算机［11］，因此得到的结果不含有漏磁作用对探头的影响。忽略速度对磁化效果的影响，可对磁化涡流检测的磁化部分独立研究。

以钢为研究对象建立三维有限元1/4模型，管道的外径为R1，厚度为W1，长度为L1，磁化线圈内径为R2，厚度为W2，长度为L2，缺陷长度为Lf，宽度为 Wf，深度为 Df；磁化线圈的电导率为σCu，相对磁导率为1，管道的电导率为σS。输入X50钢的B⁃H曲线,见图1。采用外穿过式线圈磁化管道，缺陷区域的钢管网格重点加密，逐渐向外稀疏，过渡比例控制为1/6，见图2。整个模型外层设置近远场空气层，同时在外边界施加通量平行条件，求解后通过后处理获得关注区域的电磁场分布及参量。

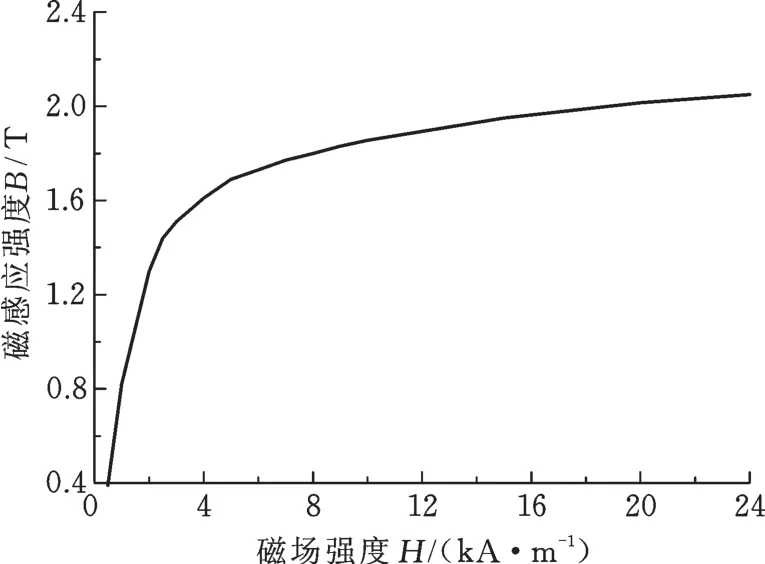
图1 钢的B⁃H曲线Fig.1 B⁃H curve of steel

图2 钢管磁化仿真模型Fig.2 Sim u lation m ode of steel pipe under m agnetization

2 仿真结果及分析

2.1 励磁强度对管道表面磁场及漏磁场的影响

设置钢管外径R1为36.5mm，厚度W1为6mm，长度L1为600 mm；励磁线圈内径R2为42.5 mm，厚度W2为20mm，长度L2为120mm；缺陷为周向短槽缺陷，位于管道内外表面的中心处，长度Lf为20 mm，宽度Wf为1mm，深度Df为1 mm，管道参数与实验所用管道参数一致。钢管的磁化涡流检测通常需要多次调节励磁线圈的励磁电流，使管道被检测区域处于磁饱和状态。仿真模拟与实验均采用励磁电流表征铁磁管道的励磁强度。图3所示为励磁电流为8～30 A时的仿真模型中心处磁感应强度的水平分量与实际钢管中心处磁感应强度水平分量。

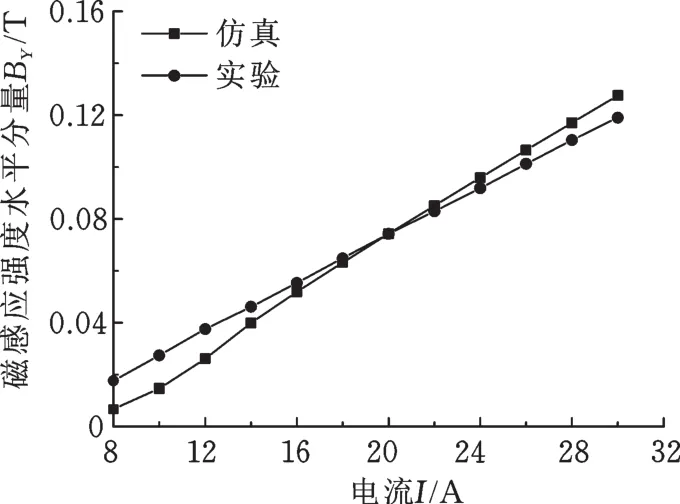
图3 仿真与实验磁场对比Fig.3 M agnetic field of sim u lation and experim ent

根据图3所示参考电流，设置励磁电流为0～34 A，步进间隔为1 A。励磁线圈产生的空间磁场对钢管实施纵向磁化时，缺陷区域的表面磁场既有线圈产生的空间磁场，也有缺陷产生的漏磁场。钢管缺陷区域的磁场为线圈产生的空间磁场与缺陷漏磁场的矢量叠加，有缺陷时与无缺陷时钢管表面磁感应强度的绝对值即为缺陷产生的漏磁场大小。设置不同的励磁电流，提取管道外表面且位于缺陷正上方3 mm位置处的磁感应强度以及管道不含缺陷时同位置处的磁感应强度，即得到磁感应强度与励磁电流I的关系，进一步可得到缺陷产生的漏磁场与励磁电流I的变化关系，见图4。提取模型中心处钢管表面单元的磁导率μ，通过公式μr= μ/μ0，其中μ0=4π × 10-7N/A2，得到相对磁导率μr。图5所示为无缺陷时钢管轴向中间位置表面的相对磁导率μr与励磁电流I的变化关系。

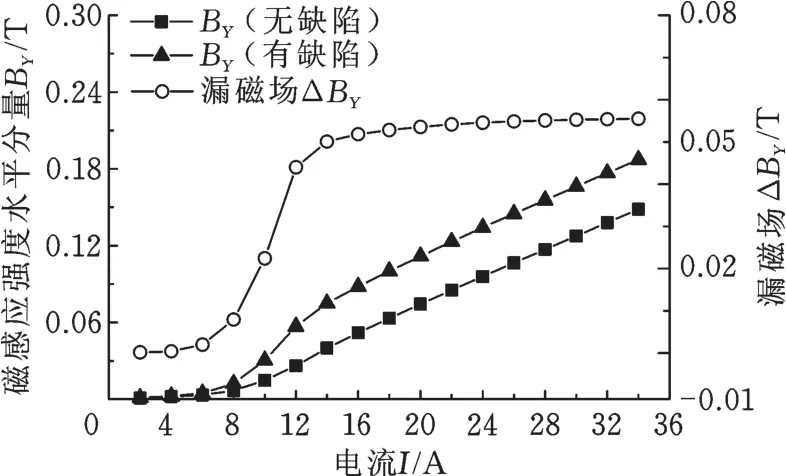
图4 钢管表面磁场与漏磁场Fig.4 Su r facem agnetic field and leakagem agnetic field of pipe

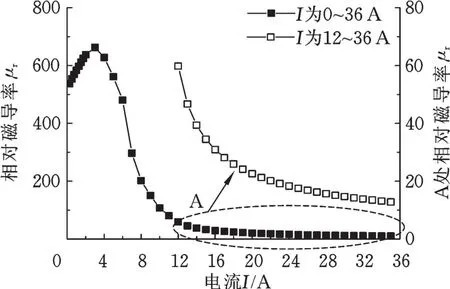
图5 铁磁管道相对磁导率与励磁电流关系Fig.5 Relativem agnetic perm eability and excitation cu rren t in ferrom agnetic pipe

由图4可以看出，励磁电流为2～4 A时管道处于初始磁化区，管道表面的磁场比较微弱，2 A时漏磁强度ΔBY仅有1.7 G，4 A时为4.3 G。电流达到6 A以后，漏磁场强度呈几何级数增大，6 A时为19 G，12 A时达到440 G。励磁电流为14 A时漏磁场强度为501 G，随后漏磁场强度随励磁电流缓慢增大，励磁电流从14 A增至34 A，漏磁场强度仅增大了6.9%。可看出，励磁电流达到14 A以后，漏磁场增加非常缓慢，按照电磁学中对磁饱和的相关定义，管道已达到磁饱和状态。

就钢管表面的相对磁导率而言，不施加磁化时管壁的相对磁导率很高，达到528。为了更清楚地观察磁导率与励磁电流的变化关系，励磁电流在0～2 A之间时步进间隔缩小为0.2 A。在0～3 A之间，相对磁导率快速增至最大值662，磁导率与励磁电流成正相关，继续增大励磁电流，磁导率迅速下降。励磁电流为16 A时仅有最大值时的7.5%，励磁电流大于16 A时，磁导率继续下降，但下降速度明显降低，励磁电流从24 A增至30 A时，磁导率下降了23.4%；励磁电流在30～34 A之间，磁导率下降了12.9%，此时虽然已经处于磁饱和的范围，但管道的磁导率仍在下降。

综合缺陷漏磁场以及钢管表面磁导率与励磁电流之间的关系可知，管道磁饱和的状态可以通过漏磁场与磁导率两个角度判定。总体趋势上，对于管道磁饱和状态的认定，漏磁法与磁导率方式是一致的。管壁的磁导率在达到磁饱和后，电流由14 A增至34 A，相对磁导率由60.5降至9.7，下降了83.9%，而漏磁场在此区间内仅增加了6.9%。从以上结果分析可知，即使管道在饱和状态，增大励磁电流还对磁导率有一定影响。

2.2 缺陷区域的磁导率分布特征

利用计算得到的钢管各网格单元的绝对磁导率μ，获得钢管模型各单元的相对磁导率μr，从而得到管道的相对磁导率的分布云图。图6、图7中给出了管道励磁电流为30 A时外壁缺陷与内壁缺陷的磁导率分布。可以看出，外壁缺陷相对磁导率最大值为378.2，最小为5.5，而内壁缺陷相对磁导率最大值为437.4，最小为5.6。内外壁缺陷周围的磁导率并非如文献中所认为的磁饱和后的管道的磁导率是均匀的，即使在深度饱和情况下缺陷附近仍然存在磁导率不均匀的区域。由于渗透深度的存在，外穿过式线圈对管道进行检测时仅能够对材料的表面和近表面进行检测，因此需要考虑缺陷对管道外表面磁导率的影响。图7a中并未观察出内部缺陷对管道外表面磁导率的影响，这是由于内壁缺陷引起钢管外壁磁导率波动相对较小，在较大范围的显示模式下难以识别其变化，因此通过映射路径的方法提取其变化可以更直观地观察出缺陷对管道外表面磁导率的影响。

图6 外壁缺陷的相对磁导率分布Fig.6 Relativem agnetic perm eability d istribution of outer defects

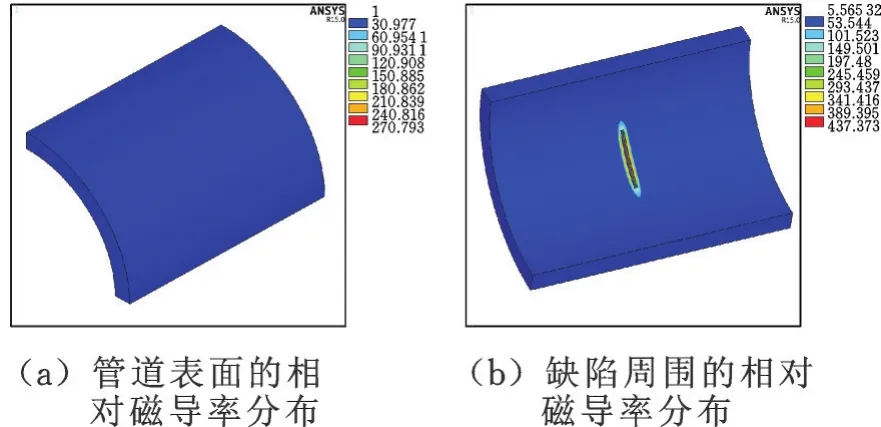
图7 内壁缺陷的相对磁导率分布Fig.7 Relativem agnetic perm eability distribu tion of inner defects

图8所示为励磁电流30 A时内外壁缺陷附近沿钢管表面轴线方向上距离管道表面不同深度处的相对磁导率分布状况。由于磁化程度的差异，管道不同深度h处相对磁导率分布状况较为复杂。对于外壁缺陷，由距离管道外表面深度h小于1 mm处的相对磁导率的分布可以看出，相对磁导率以缺陷中心位置为起始沿轴线向两侧迅速减小。缺陷位置深度h=0.5mm处相对磁导率峰值大于h=0.1mm处相对磁导率峰值，0.1 mm处相对磁导率峰值为104.86，0.5mm处峰值为106.87。随着深度的增大,管道远离缺陷处的相对磁导率稍有增大但基本趋于一致，而缺陷位置的相对磁导率峰值却迅速减小，h=2 mm位置的相对磁导率峰值为19.7，仅为0.1 mm处峰值的18.7%。同时缺陷附近相对磁导率峰-峰值之间的宽度要大于缺陷自身的几何宽度，h为0.1mm、0.5mm、1mm处的峰-峰值宽度为1.5mm，而h为2mm处的峰-峰值宽度甚至大于3mm。随着深度的增大，深度大于2mm后相对磁导率反而仅有极小值。

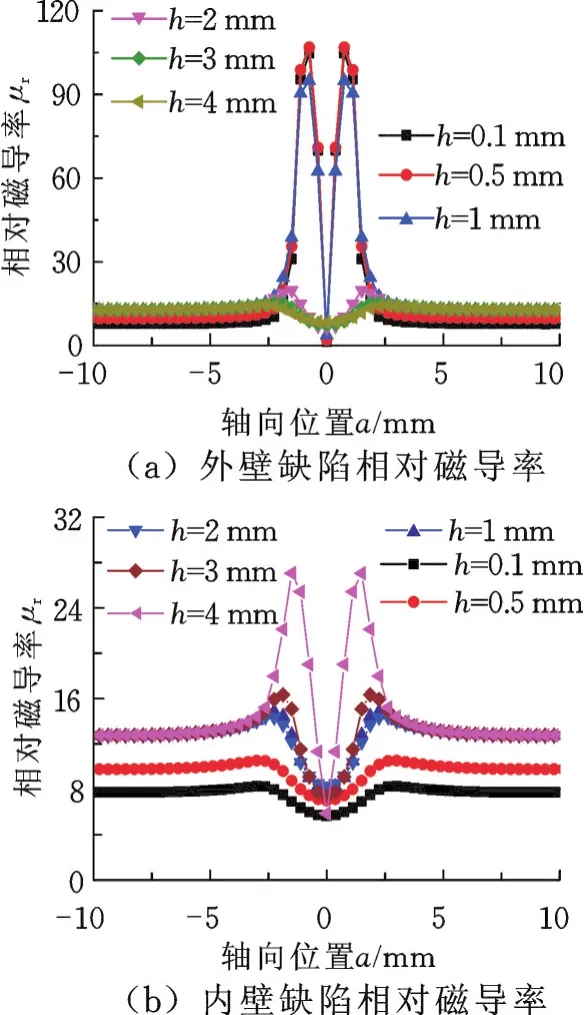
图8 励磁电流30 A时不同深度的相对磁导率Fig.8 Relativem agnetic perm eability of differen t dep th under I=30 A

对于内壁缺陷来说，通过获取距管道外壁为0.1～2 mm处的相对磁导率分布可以看出，内壁缺陷的存在引起了钢管外表面磁导率的改变，缺陷正上方位置磁导率有极小值。h=0.1 mm处，管壁的相对磁导率约为7.76，路径上相对磁导率最大值为8.2，最小为5.63，相对磁导率最大值与最小值之间的差值为2.57。深度增至0.5 mm时，远离缺陷处相对磁导率增至12.8，最大值与最小值的差值增至5，但靠近缺陷区域的相对磁导率变化最为剧烈。对于涡流检测而言，内部缺陷的存在引起的钢管表层磁导率不均匀分布可能引起涡流探头产生信号响应，这也是管道在饱和条件下能够检测到趋肤深度外的内部缺陷的原因。

2.3 励磁强度对缺陷区域磁导率的影响

励磁电流I分别取为10 A、14 A、18 A、22 A、26 A、30 A，模型其他参数不变，设置路径深度为0.15 mm，得到钢管近表面磁导率与励磁电流的对应关系，见图9。

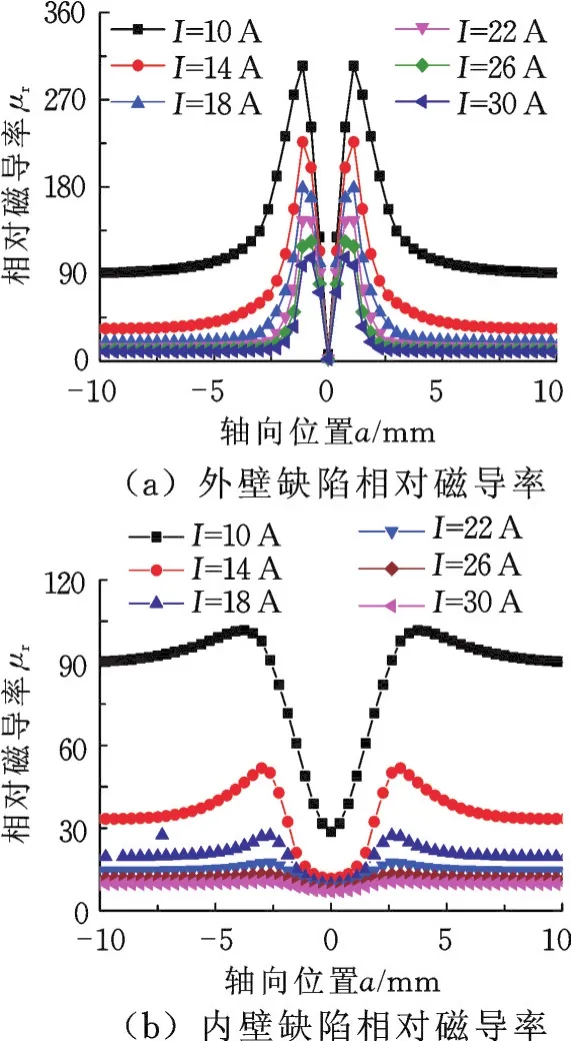
图9 不同励磁电流下的相对磁导率分布（h=0.15mm）Fig.9 Relativem agnetic perm eability distribution w ithd ifferen t excitation cu rren t（h=0.15mm）

管道的磁导率与励磁电流成负相关，随着励磁电流的增大，内外表面缺陷附近的磁导率以及远离缺陷处的磁导率迅速下降。外壁缺陷的相对磁导率峰-峰值间距约为3 mm，但随着励磁电流的增大而减小，10 A时约为3.06，30 A时约为2.94，仅减小了4%。对内壁缺陷而言，励磁电流为14 A时，区域宽度为8.6 mm，而电流为30 A时，区域宽度为4 mm，下降了54%，说明励磁电流越大，磁导率发生改变的区域宽度越小。随着励磁电流的增大，内部缺陷对管壁处磁导率的影响越小，电流为10 A时，管壁相对磁导率与远离缺陷处的磁导率的差值为72；电流为22 A时，差值为39；电流为30 A时，差值为3.1，分别下降了45%和94%。以上说明励磁电流越大，内部缺陷对管壁的磁导率影响越弱，电流为30 A时甚至可以忽略磁导率的差异，从而避免内壁缺陷引起的表面磁导率改变对外表面缺陷涡流检测带来的干扰。励磁电流较小时，内壁缺陷引起管道外表面磁导率的差异较为明显，内部缺陷引起材料表面磁导率的差异不能忽略，有利于涡流方法对材料内部缺陷实施涡流检测。图10与图11分别为外壁、内壁缺陷在励磁电流为10 A和30 A时涡流检测试验结果，可以看出与理论分析较为一致。

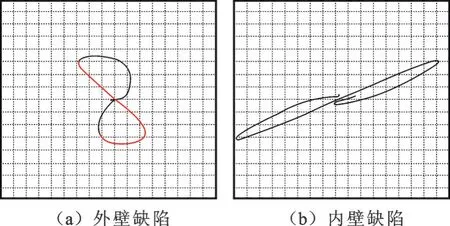
图10 10 A电流下的涡流检测结果FIg.10 Eddy cu rren t testing resu lts under I=10 A

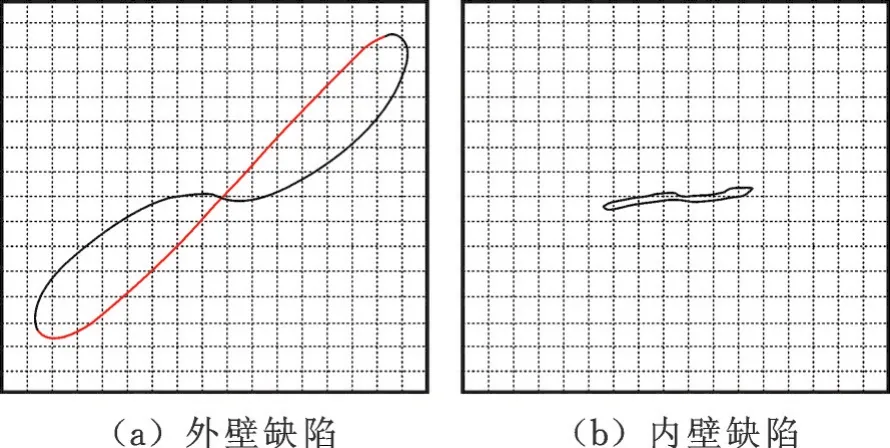
图11 30 A电流下的涡流检测结果FIg.11 Eddy cu rren t testing resu lts under I=30 A

2.4 壁厚对缺陷区域磁导率的影响

设置管道的壁厚为9 mm，缺陷尺寸不变，得到管道壁厚为9 mm时不同磁化程度下内外壁缺陷的磁导率分布情况，见图12。

将图12与图9（管道壁厚为6mm）对比可知，壁厚为9mm的管道其远离缺陷处的磁导率明显大于壁厚6mm同部位磁导率，即壁厚9 mm管道的磁化程度较壁厚6 mm管道的磁化程度弱。外壁缺陷的缺陷尺寸不变，不同壁厚的钢管其在缺陷附近的磁化程度不同。当电流为14 A时，壁厚为9mm管道相对磁导率峰值达到284，较壁厚为6mm时增大了42%；当电流为22 A时，壁厚为9 mm、6mm管道相对磁导率峰值分别为138和116。对于内壁缺陷，当励磁电流为10 A与12 A时，壁厚为9 mm管道其表层磁导率并未出现双峰现象，而励磁电流为16 A时，磁导率才开始有双峰值，同磁化电流下壁厚为9mm管道其内壁缺陷磁导率最大值与最小值的差值也随励磁电流的增大而减小，但厚度为9 mm管道其磁导率差值较6mm管的差值略小。综上，随管道厚度的增加，厚壁管因对磁感线的约束程度较弱使得管道整体的磁化水平较6 mm管道弱，因而影响励磁条件下缺陷区域磁导率的分布状况。

2.5 缺陷深度对缺陷区域磁导率的影响

设置励磁电流I分别为14 A和28 A，缺陷深度d分别为1mm、2mm、3mm，管道壁厚为6mm时内外壁缺陷的相对磁导率分布见图13。

从图13中可以看出，不同深度的外壁缺陷其磁导率的差异不仅体现在峰值上，缺陷深度越深，其磁导率峰值越大，同时其磁导率发生改变的范围也较大。当励磁电流为10 A时，由于管道磁化程度较弱，磁感线受约束程度较弱因而其辐射的范围较广；当励磁电流增至28 A时，由于磁力线被强烈压缩，缺陷区域磁导率发生改变的区域也有所减小。对于相同磁化程度不同深度的内壁缺陷，其表层磁导率改变较小，两种不同的磁化状态下，其对应的三种深度的缺陷附近的磁导率值近乎相同。

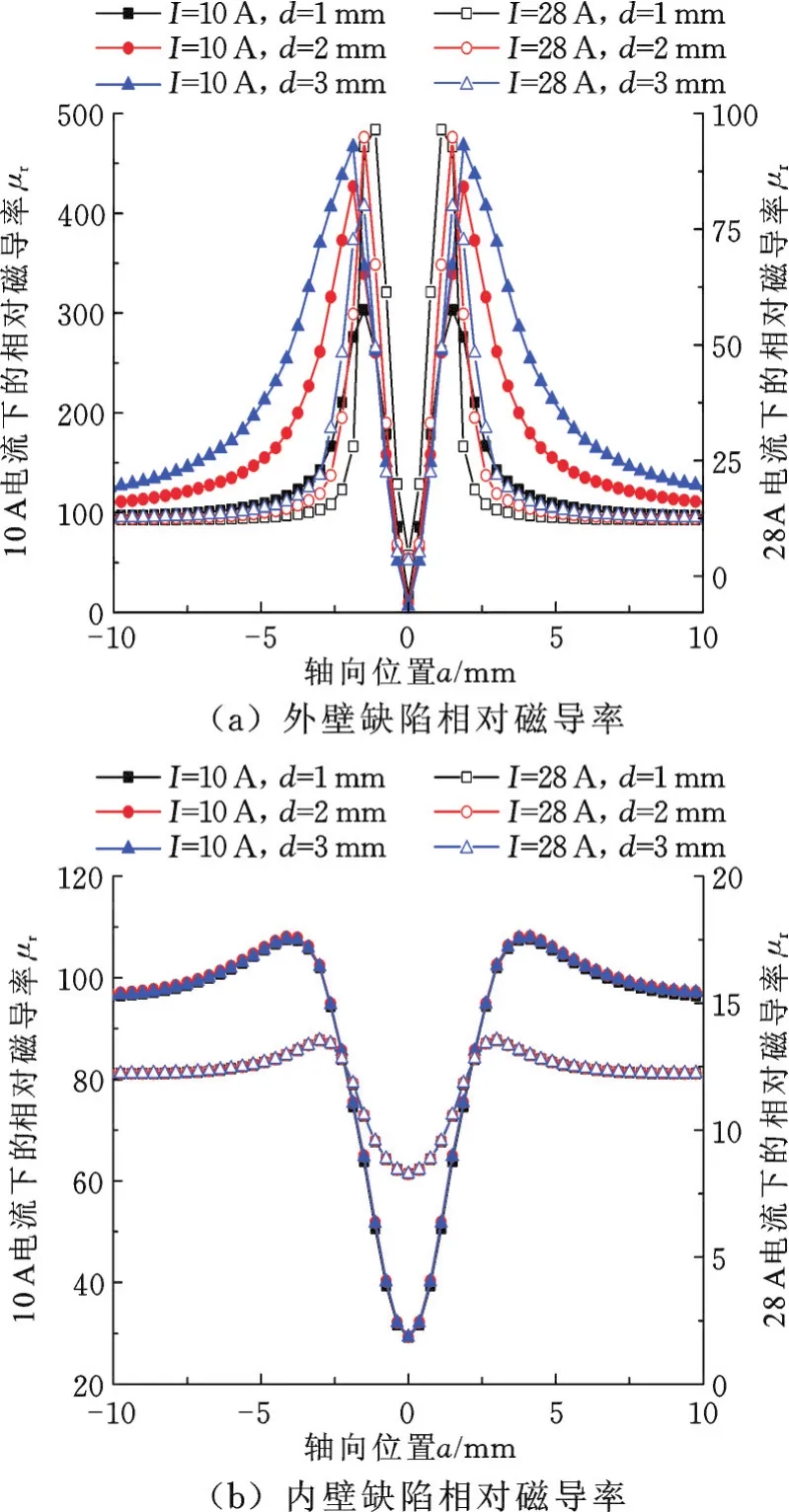
图13 不同缺陷深度时的相对磁导率分布Fig.13 Relativem agnetic perm eability d istribu tion w ith different dep th of flaw

2.6 分析与讨论

由上述结果可以看出，铁磁材料在磁饱和状态时，并没有呈现出与标准中所说的缺陷周围磁导率是均匀的现象，因此不能将其当做非铁磁性材料看待。在饱和状态时，缺陷磁导率仍然不均匀，即使材料处于深度磁饱和状态，缺陷周围的磁导率也不是均匀的。

从漏磁检测角度考虑，铁磁材料中缺陷的存在引起磁场的畸变，由于铁磁材料的磁阻远小于空气的磁阻，部分磁感线绕过缺陷从缺陷附近的材料中通过且经过母材绕过缺陷的磁感线要远多于经过空气中的磁感线。如图14所示，深度方向上大部分磁感线从缺陷下部通过，而缺陷端部的磁感线则大多从端部的母材中通过，因此造成该区域的磁感线相对密集，在原有磁化强度的基础上，引起该部位磁化程度比无缺陷处的磁化程度更强。

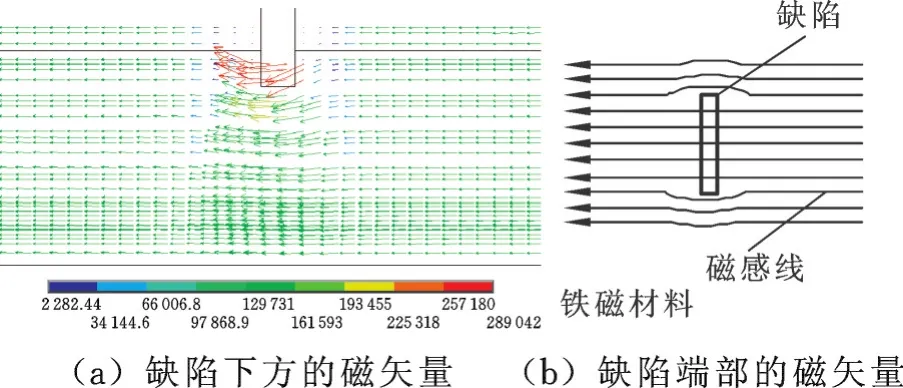
图14 缺陷附近的磁矢量Fig.14 M agnetic vector around the defect

根据铁磁材料的μ⁃H关系可知，磁导率是磁化强度H的函数，缺陷附近磁化程度的差异必然导致磁导率的分布不均。材料达到磁饱和后，磁导率随磁化强度的增加而减小的程度依然较为明显，磁化强度的微弱增大也会引起磁导率发生较大的改变。趋近饱和区时，材料的磁导率随磁化强度改变尤为明显，而此时外界磁场较弱，材料内以及缺陷附近材料中的磁感线相对稀疏，缺陷引起磁感线变化的范围较大，内部缺陷也能引起材料表面产生漏磁场，同时造成表面处磁导率的不均匀。励磁电流增大时，大量的磁感线被压缩在铁磁材料有限空间内，缺陷附近磁化程度不均匀的范围也逐步缩小，从而造成磁导率不均匀的范围缩小，同时磁感线聚集造成的磁化强度的增大导致整体磁导率的下降，因而在励磁强度越大的情况下，内壁缺陷和外壁缺陷磁导率最值降低。

由图8、图9可以看出，即使在磁饱和直流磁化下，无论外壁缺陷还是内壁缺陷，在其边缘区域磁导率仍处于非均匀状态，导致磁导率局部发生畸变，因此进行涡流检测时，外壁缺陷受缺陷处电导率变化、缺陷边缘磁导率畸变和临近缺陷区均匀磁导率的共同作用，在不同的磁场强度下，三者的影响有不同程度的增大或减小，这样使涡流检测阻抗信号相位随之变化；而内壁缺陷仍仅有缺陷因磁化导致的不均匀磁导率扩散至外壁而被检出，因而信号的影响因素较为单一，选择合理的磁化电流将有利于区分两种不同位置的缺陷。

3 结论

（1）采用有限元方法，建立了含有内外表面缺陷钢管磁化的三维局部分析模型，研究了管道漏磁场与磁导率随励磁电流的变化关系。对管道内壁缺陷和外壁缺陷区域在不同励磁状态下的磁特性进行了分析。

（2）铁磁管道处于磁饱和时，外界磁场强度的改变对漏磁场影响不大。而磁导率在管道达到磁饱和后，虽然数值上变化不大，但励磁强度对磁导率变化率的影响依然较为明显。

（3）磁饱和时，管道缺陷区域的磁导率并非标准中描述的是均匀的，受磁化强度差异的影响，缺陷周围母材的磁导率分布较为复杂，内壁缺陷的存在造成缺陷周围的磁导率不均匀可影响外表面磁导率分布。通常认为的饱和磁化，缺陷区域的饱和程度远未达到。

（4）在非饱和磁化下，内壁缺陷能够对外表面磁导率造成较为明显的影响，但随磁饱和程度的增加而减弱。工程中为抑制管道内部缺陷对表面缺陷检测的干扰，可在管道饱和磁化的基础上进一步提高励磁电流。为了对管道内部缺陷进行检测，在磁饱和的基础上采用较小的励磁电流，同时对表面和内部缺陷进行检测。