高速铁路CRTSⅢ型板式无砟轨道减振垫层动力影响及结构优化
辛 涛,张 琦,高 亮,赵 磊,曲建军
(1.北京交通大学 土木建筑工程学院,北京 100044;2.轨道工程北京市重点实验室,北京 100044;3.北京市轨道交通线路工程安全与防灾工程技术研究中心,北京 100044;4.中国铁道科学研究院 铁道建筑研究所,北京 100081;5.中国铁道科学研究院 基础设施检测研究所,北京 100081)
随着我国高速铁路的快速发展,无砟轨道得到了广泛应用,列车速度不断提高,列车振动荷载作用下无砟轨道及下部基础的振动噪声问题逐渐引起人们的关注。相对有砟轨道,无砟轨道的振动噪声问题更加突出。研究表明,无砟轨道的振动噪声一般比有砟轨道振动大5 dB[1]。
在无砟轨道的减振措施方面,日本、德国等国家较早开展了相关设计和研发工作。日本铺设了各种防振型轨道,如在日本的东北和上越新干线铺设的防振A型轨道和防振G型轨道,采用了不同减振材料做垫层。德国发明了浮置板式减振轨道,并在其高速铁路上铺设了旭普林浮置板轨道,减振效果较为良好。我国在无砟轨道减振方面也做了相关研究,为控制和减小无砟轨道的振动和噪声采取了很多措施,如采用减振扣件、阻尼钢轨、弹性支承块式轨道等[2]。
针对高速铁路振动问题,相关学者对不同轨道结构振动传递特性进行了针对性的研究。马学宁等建立了高速铁路板式无砟轨道—路基模型,对结构动力特性进行了研究,重点讨论了路基动应力变化特点[3]。杨新文等针对双块式无砟轨道建立了车辆—轨道—路基动力模型,分析了无砟轨道和路基的振动传递特性,重点从频域分析了结构的振动衰减规律[4]。Dai建立了高架桥上CRTSI型和浮置板式2种无砟轨道模型,对比了不同参数的减振效果[5]。Kuo等进行了浮置板轨道扣件垫板刚度、轨道板垫层刚度及列车运行速度等参数对钢轨、轨道板振动影响分析[6]。孙文静建立了车辆轨道垂向耦合动力学模型,对刚性轨道和离散支撑轨道进行了对比分析[7]。
CRTSⅢ型板式无砟轨道是我国高速铁路的新型无砟轨道结构。在CRTSⅢ型板式无砟轨道振动研究方面,王明昃等研究了轨道板服役期间混凝土弹模改变对轨道—路基系统的动力影响[8]。陈江等对高速移动荷载下桥上铺设CRTSⅢ型无砟轨道结构的动力响应进行了仿真模拟[9]。周毅对CRTSⅢ型无砟轨道铺设减振垫层的减振效果进行了讨论[10]。张光明对最早铺设于成灌快线铁路的CRTSⅢ型无砟轨道桥梁段的环境振动问题做了试验研究[11]。这些研究虽没有关注垫层不同设置位置的影响,但可为本文的研究提供一定的参考。
本文在既有研究的基础上,利用谐响应和车轨耦合分析手段,重点研究减振垫层不同设置方案对无砟轨道动力响应的影响,并进一步提出垫层优化建议。
1 结构分析模型
根据CRTSⅢ型无砟轨道及减振垫层的结构特点,建立CRTSⅢ型无砟轨道精细化分析模型。CRTSⅢ型板式无砟轨道系统从上至下由钢轨、扣件、轨道板、自密实混凝土和底座板构成。其中,钢轨采用梁单元模拟,扣件简化为弹簧—阻尼单元,轨道板、自密实混凝土、底座板以及减振垫层采用实体单元模拟。
本文主要对自密实混凝土下设置减振垫层(下称减振方案A)、底座板下设置减振垫层(下称减振方案B)和无减振垫层3种方案进行分析。根据减振方案分别建立相应的结构分析模型,图1给出了采用减振方案A和方案B的无砟轨道结构模型示意图。
对于车辆模型的处理,本文基于多体动力学理论,将车辆视为由车体、转向架、轮对多个刚体及一系、二系弹簧组成的多刚体运动体系。根据高速列车的结构特点,考虑车体和前后转向架的沉浮、点头、横移、侧滚和摇头运动,轮对的沉浮、横移、侧滚和摇头运动,则车辆模型共有31个自由度[12]。车辆模型如图2所示。
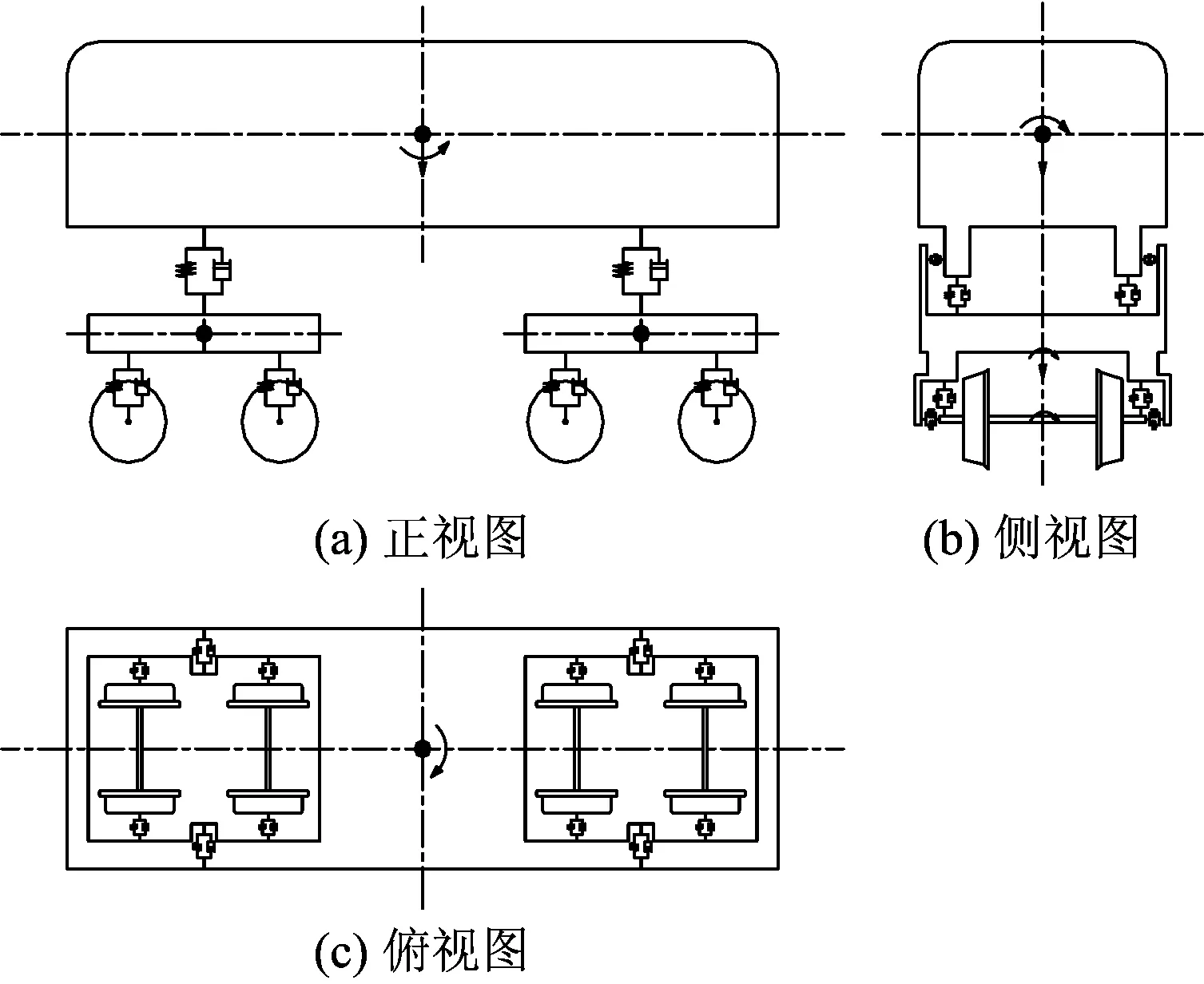
图2 车辆模型示意图
2 分析方法
2.1 谐响应分析方法
谐响应分析是用于分析结构在承受简谐荷载时稳态响应的一种方法,通过分析得到结构的频率响应曲线。谐响应只计算结构的稳态受迫振动,不考虑发生在激励开始时的瞬态振动。受迫振动时,结构体系运动微分方程的一般形式为
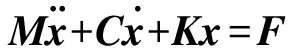
(1)
式中:M,C和K分别为质量、阻尼和刚度矩阵;F为外荷载向量;x为位移响应向量。
假设外荷载和位移响应为简谐形式,即
F=Fmaxejψejωt
(2)
x=xmaxejφejωt
(3)

激励荷载可用实部和虚部表示为
F=Fmaxejψejωt
=(Fmaxcosψ+jFmaxsinψ)ejωt
=(F1+jF2)ejωt
(4)
位移响应也可与激励荷载类似用实部和虚部表示为
x=(x1+jx2)ejωt
(5)
其中,
x1=xmaxcosφ,x2=xmaxsinφ
将式(4)和式(5)带入运动微分方程(1)中,可得
(-ω2M+jωC+K)(x1+jx2)=(F1+jF2)
(6)
由上式可解得结构位移响应的实部和虚部,进而得到其幅值和相位。
在激励作用点p施加简谐荷载,提取节点q的位移响应,则位移导纳可以表示为
(7)
2.2 车辆轨道耦合分析方法
常见的车辆动力学和有限元分析软件在进行车辆、轨道和下部结构的建模时都存在一定的不足,如车辆动力学仿真软件一般不能进行轨道和下部结构的细致模拟;而有限元分析软件不含轮轨接触模块,也难以进行车辆的多体动力学建模。针对既有商业软件的不足,作者利用自主开发的动力仿真计算平台FORSYS[13],实现了车辆(多刚体模型)和轨道(有限元模型)的“刚柔耦合”。多刚体模型、有限元模型的运动方程都能写成如下的矩阵形式。
(8)
(9)
式中:下标m和f分别表示多刚体(MBS)和有限元(FE)模型。
FORSYS可以读入多刚体模型和有限元模型的质量、刚度和阻尼矩阵,采用我国高速铁路不平顺谱作为激励,并按照轮轨实际接触条件计算轮轨接触力,形成系统的荷载列阵,进而通过“对号入座”形成耦合系统的运动方程。
(10)
利用Newmark方法求解系统运动方程,采用迭代的方法求解获得系统各部分的动力响应。首先,基于上一荷载步得到车轮、钢轨的位移和轮轨接触点的轨道不平顺等参数,利用轮轨接触相关理论[12]计算得到当前荷载步新的轮轨力,对运动方程进行求解,得到新的车轮、钢轨位移等动力响应。然后,在此基础上对轮轨力进行迭代求解,当误差小于1%时则认为计算收敛。在相同计算条件下,将仿真结果与相关文献结果进行对比[12-13],验证了本模型和计算方法的可行性。
3 仿真计算结果分析
基于所建立的动力分析模型,首先利用谐响应分析方法研究减振垫层设置位置的影响,进而利用车辆轨道耦合分析方法对列车通过时轨道系统的动力响应进行分析,最后对建议方案进行结构优化。
3.1 谐响应结果分析
利用所建立的CRTSⅢ型无砟轨道精细化分析模型,选取沿线路延伸方向中间截面的钢轨节点,施加不同频率的激励荷载,计算得到钢轨、轨道板及路基顶面的位移导纳。不同方案减振垫层的刚度均取100 MPa·m-1。
图3给出了非减振方案和减振方案A、减振方案B下,钢轨、轨道板和路基顶面的位移导纳曲线。
由图3可知,对于非减振方案,从钢轨到轨道板和路基顶面,位移导纳降低明显,而轨道板和路基的位移导纳差别不大,尤其是在100 Hz以下的低频范围内,二者几乎一致。
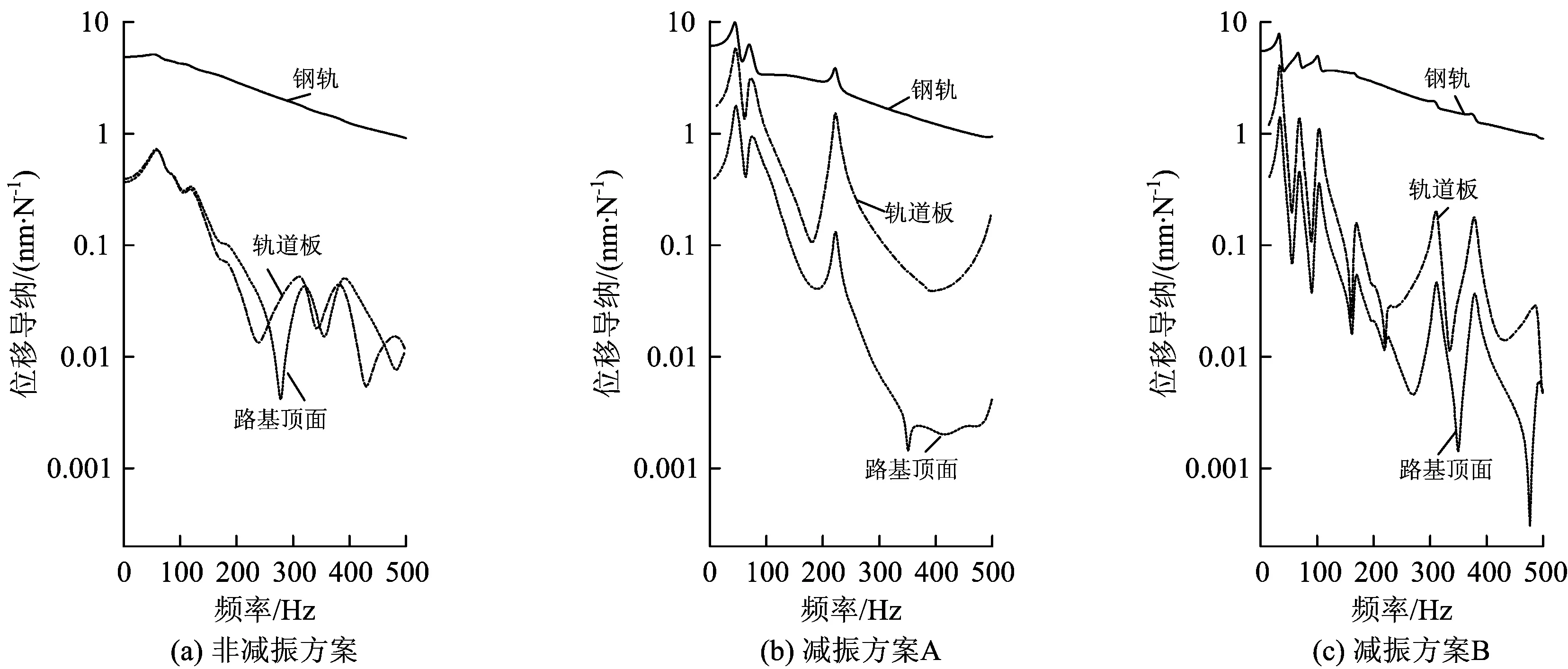
图3 不同减振方案条件下,钢轨、轨道板和路基顶面的位移导纳曲线
对于2种减振方案,从钢轨到轨道板、从轨道板到路基,位移导纳逐步衰减;与非减振方案相比,钢轨位移导纳差别不大,但轨道板位移导纳有所增大。
路基振动为低频振动,主要考虑200 Hz以内的减振效果。对200 Hz以内路基顶面位移导纳进行对比,结果如图4所示。由图4可以看出,当振动频率大于40 Hz时,采用减振方案B时路基顶面的位移导纳整体小于采用非减振方案。故相对于减振方案B,减振方案A的减振范围较小,但是这2种减振方案的路基位移导纳在100~200 Hz范围内均小于非减振方案。
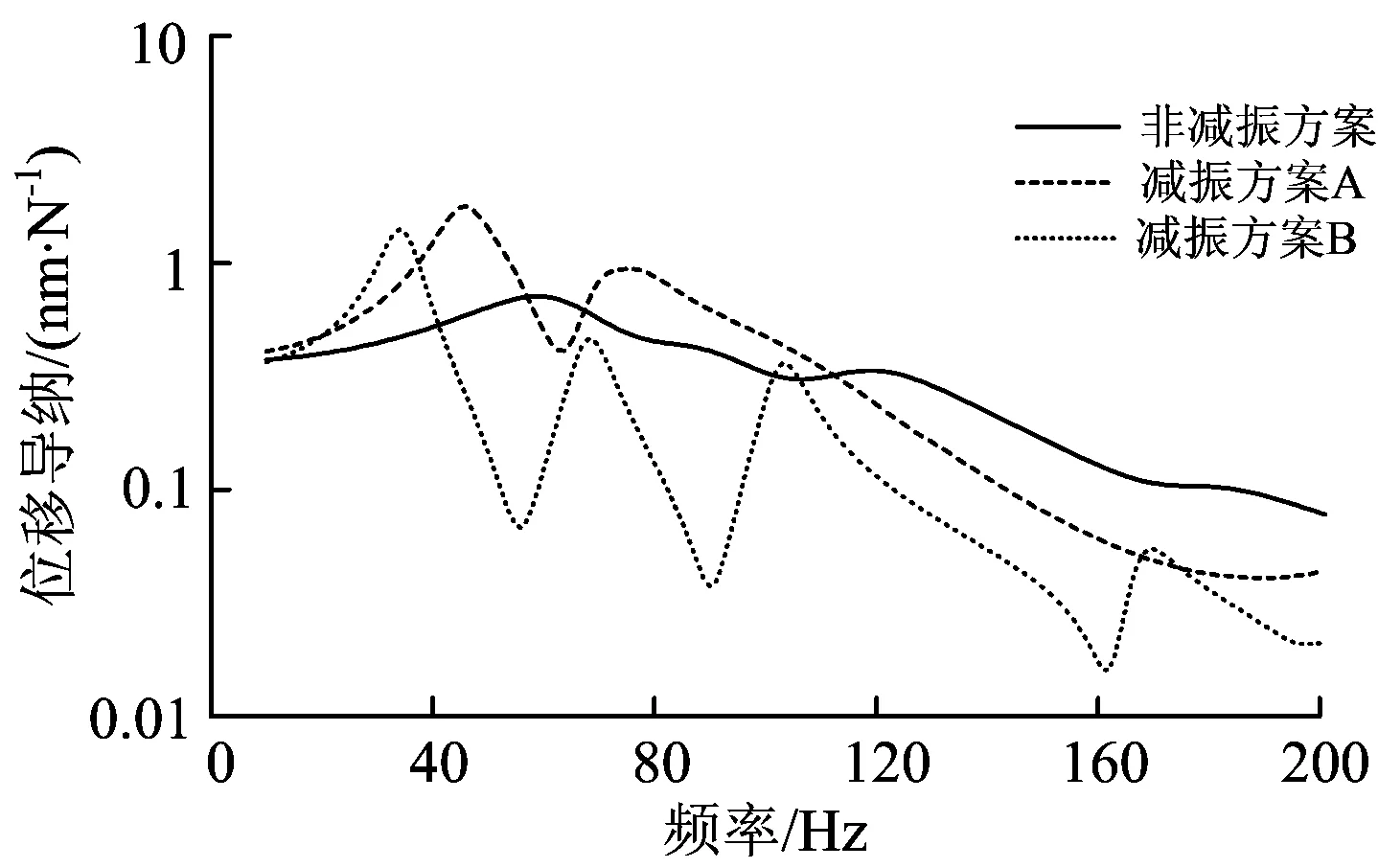
图4 不同减振方案下路基顶面的位移导纳
谐响应分析结果表明,减振垫层对无砟轨道的动力影响主要体现在轨道板、路基上;从降低对路基等下部基础结构及环境的影响来看,减振方案B好于减振方案A。
简谐荷载形式较为简单,上述谐响应分析为初步分析,还不足以充分证明减振效果。为了与实际情况更为接近,下面通过车辆轨道耦合分析,进一步对减振效果进行分析。
3.2 车辆轨道耦合结果分析
利用车辆轨道耦合模型,分析列车高速通过时不同减振方案的减振效果。列车运行速度为350 km·h-1,减振垫层刚度取100 MPa·m-1。
表1为车体垂向加速度和轮轨力的计算结果。由于轮轨力一般较为离散,因此表1中同时给出了轮轨力的最大值和有效值。由表1可以看出,减振垫层对车辆动力响应的影响很小。
表2为列车运行时钢轨、轨道板、路基顶面加速度的计算结果。其中,路基顶面加速度为200 Hz低通滤波后结果。为了使结果更具可比性,在进行不同减振方案的对比计算时选取了同一位置的计算结果,而且考虑到加速度响应具有一定的离散性,表中同时给出了加速度的最大值和有效值。由表2可以看出,减振垫层对钢轨动力响应的影响很小,影响主要体现在轨道板和路基上。
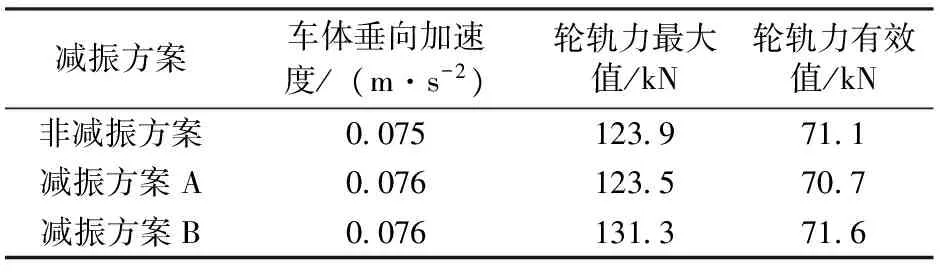
表1 车辆动力响应
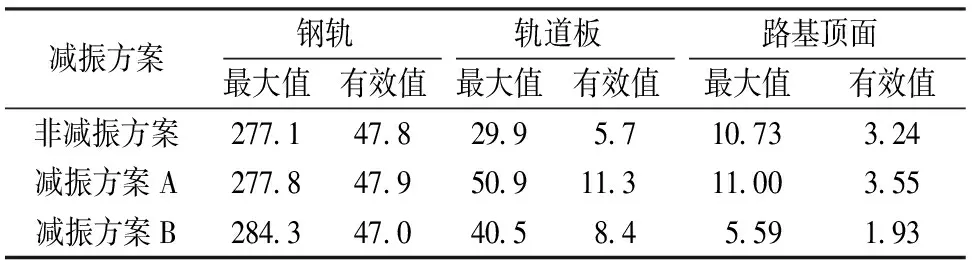
表2 轨道结构的加速度响应 m·s-2
与非减振方案相比,减振方案A和减振方案B都增大了轨道板的振动,而降低了路基的振动。本文选用减振垫层方案时重点考虑了其对下部结构及环境的影响,因此,结合表2中的计算数据,减振方案B效果更好。
图5和图6分别给出了不同减振方案下路基顶面加速度时程曲线和频谱曲线。
从时域计算结果可以看出,减振方案B相对非减振方案,路基顶面加速度有效值降低约40%,减振效果显著,而减振方案A减振效果略差。
从频域分析结果可以看出,3个方案均在78 Hz出现峰值,该频率对应波长1.25 m(350/3.6/78),正好为转向架轴距之半,可以判定该峰值与车轮激励相关。在200 Hz以内,采用减振方案B时路基加速度谱密度整体上小于非减振方案时,减振效果最优,而且在100~200 Hz范围减振效果最为明显,与谐响应分析结果一致。
3.3 减振垫层刚度优化分析
下面在减振方案B基础上,通过改变垫层刚度,研究其对减振效果的影响。参考相关文献[14-16],阻尼在一定范围内增加对减振效果的影响不明显,因此本文主要分析垫层刚度对减振效果的影响,垫层阻尼按照固定值选取。列车速度仍为350 km·h-1,垫层刚度分别取为20,50,80,100,200和300 MPa·m-1。
一般认为,垫层刚度越小,减振效果越好,但同时钢轨位移越大,因此,选取路基顶面加速度、钢轨位移分别作为垫层刚度优化的减振效果和变形控制指标。图7给出了不同垫层刚度条件下路基加速度和钢轨位移的计算结果。
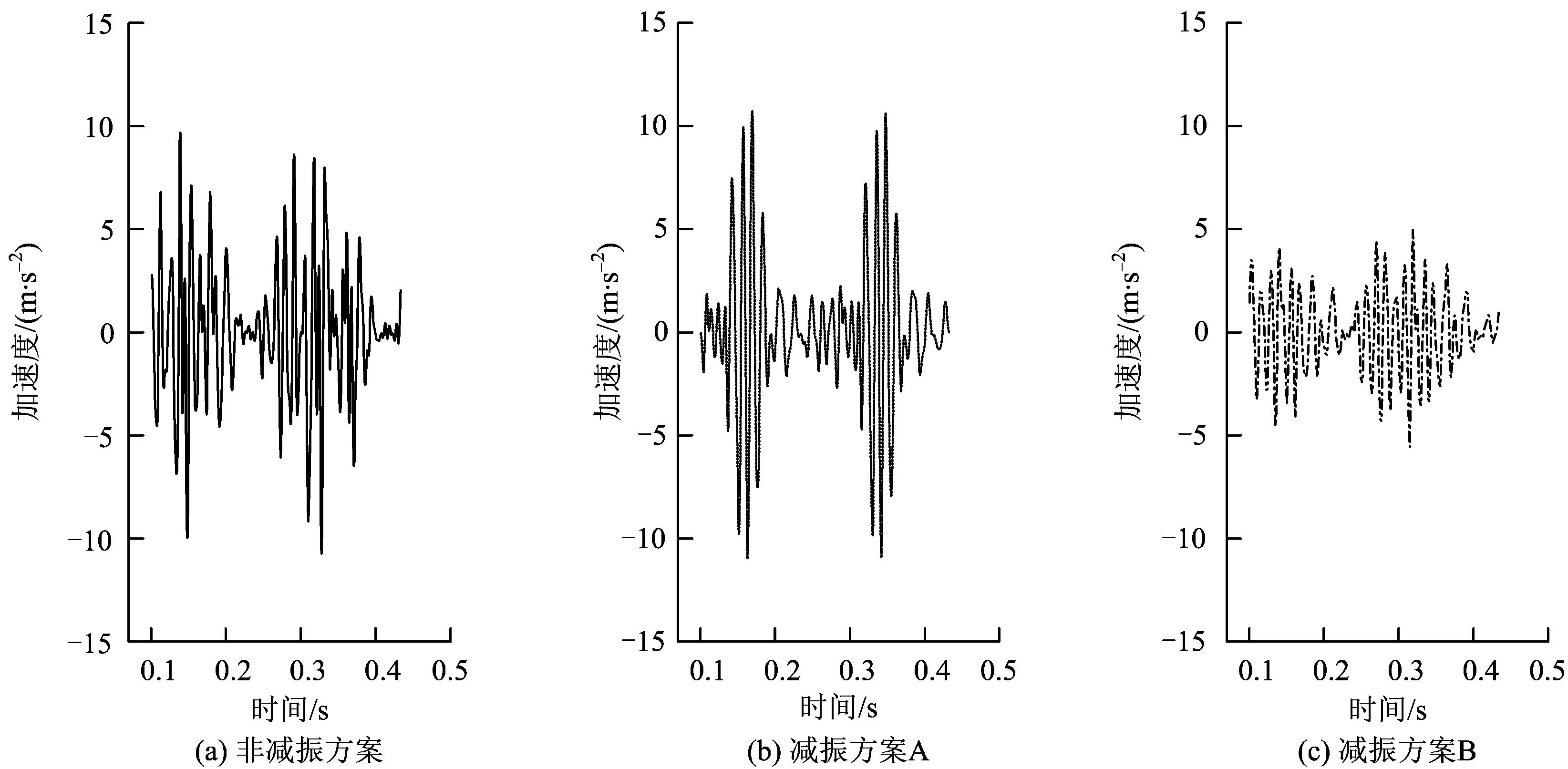
图5 不同减振方案条件下路基顶面加速度时程曲线

图6不同减振方案条件下路基顶面加速度频谱曲线
由图7可知,随着垫层刚度的增大,路基加速度呈非线性增大趋势,而钢轨位移呈非线性减小趋势。为了尽量提高减振效果,同时兼顾钢轨变形控制,建议垫层刚度取为50~80 MPa·m-1。
4 结 论
(1)无砟轨道减振垫层的动力影响主要体现在轨道板、路基上;在自密实混凝土和底座板下设置减振垫层都可以起到减振作用,减振效果主要体现在100~200 Hz范围;车辆轨道耦合分析与谐响应分析结论一致,互为支撑。

图7 不同垫层刚度下的计算结果
(2)从基础和环境减振的角度,基于时域、频域的分析结果表明,底座板下设置减振垫层的方案更优。
(3)综合考虑减振效果和钢轨变形控制,减振垫层的刚度建议取50~80 MPa·m-1。
[1]ANDO K, HORIIKE T, KUBOMURA K, et al. Present Status on Slab Track and Environmental Countermeasures[J]. Quarterly Report of RTRI, 1996, 37(4): 204-209.
[2]练松良.轨道工程[M].北京:人民交通出版社,2009.
(LIAN Songliang. Railway Track [M]. Beijing: China Communications Press, 2009.in Chinese)
[3]马学宁,梁波,高峰.高速铁路板式无砟轨道—路基结构动力特性研究[J].铁道学报,2011,33(2):72-78.
(MA Xuening, LIANG Bo, GAO Feng. Study on the Dynamic Properties of Slab Ballastless Track and Subgrade Structure on High-Speed Railway[J]. Journal of the China Railway Society, 2011, 33(2): 72-78. in Chinese)
[4]杨新文,宫全美,周顺华,等.高速列车作用下双块式无砟轨道与路基垂向耦合振动分析[J].铁道学报,2014,36(8):75-83.
(YANG Xinwen, GONG Quanmei, ZHOU Shunhua, et al. Analysis on Vertical Vibration of Coupled Double-Block Ballastless Track and Subgrade System under High Speed Train Running[J]. Journal of the China Railway Society, 2014, 36(8): 75-83. in Chinese)
[5]DAI F, THOMPSON D J, ZHU Y, et al. Vibration Properties of Slab Track Installed on a Viaduct[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2016,230(1):235-252.
[6]KUO C M, HUANG C H, CHEN Y Y. Vibration Characteristics of Floating Slab Track[J]. Journal of Sound and Vibration, 2008, 317(3/4/5): 1017-1034.
[7]孙文静,周劲松,宫岛.基于格林函数法的车辆—轨道垂向耦合系统随机振动分析[J].中国铁道科学,2015,36(1):61-67.
(SUN Wenjing, ZHOU Jinsong, GONG Dao. Analysis on Random Vibration of Vehicle-Track Vertical Coupling System with Green Function Method[J]. China Railway Science, 2015, 36(1): 61-67. in Chinese)
[8]王明昃,尹镪,朱胜阳,等.冲击荷载作用下CRTSⅢ型板式轨道—路基系统动力特性研究[J].中国科学:技术科学,2014,44(7):722-728.
(WANG Mingze, YIN Qiang, ZHU Shengyang, et al. Dynamic Analysis of CRTSⅢ Slab Track-Subgrade System under Impact Load [J]. Science China: Technological Sciences, 2014, 44(7): 722-728. in Chinese)
[9]陈江,李成辉,黄家聪.高速移动荷载作用对桥上轨道竖向动力特性的影响[J].铁道建筑,2014(6):126-129.
(CHEN Jiang, LI Chenghui, HUANG Jiacong. Influence of High Speed Moving Load on Track Vertical Dynamic Performance [J]. Railway Engineering, 2014(6): 126-129. in Chinese)
[10]周毅.CRTSⅢ型板式轨道减振特性研究[D].成都:西南交通大学,2011.
(ZHOU Yi. Research on Vibration-Reduction Performance of CRTSⅢ Slab Ballastless Track [D].Chengdu:Southwest Jiaotong University, 2011. in Chinese)
[11]张光明,贺玉龙,梅昌艮,等.CRTSⅢ型板式无砟轨道桥梁段环境振动测试分析[J].噪声与振动控制,2014,34(3):144-147.
(ZHANG Guangming, HE Yulong, MEI Changgen, et al. Measurement and Analysis of Environmental Vibration in Railway Bridge Section of CRTSⅢ Slab Ballastless Track [J]. Noise and Vibration Control, 2014, 34(3): 144-147. in Chinese)
[12]翟婉明.车辆—轨道耦合动力学[M].3版.北京:科学出版社,2007.
(ZHAI Wanming. Vehicle-Track Coupling Dynamics [M]. 3rd ed. Beijing: Science Press, 2007. in Chinese)
[13]辛涛.高速铁路高架桥上无砟道岔动力特性研究[D].北京:北京交通大学,2011.
(XIN Tao. Research on Dynamic Characteristics of Ballastless Turnouts on Viaducts in High Speed Railway [D]. Beijing: Beijing Jiaotong University, 2011. in Chinese)
[14]袁俊.地铁浮置板轨道结构减振研究[D].西安:西安建筑科技大学,2008.
(YUAN Jun. Study on Vibration Isolation Performance of the Floating Slab Track System in Metro Lines [D]. Xi’an: Xi’an University of Architecture and Technology, 2008. in Chinese)
[15]钟阳龙,蔡小培,高亮,等.铁路地下直径线橡胶浮置板道床钢轨变形限值研究[J].中国科技论文,2014,9(11):1306-1309.
(ZHONG Yanglong,CAI Xiaopei,GAO Liang, et al. Research on Rail Deformation Limit of Rubber Floating Slab Track Bed on Railway Underground Transit Line[J].China Sciencepaper,2014,9(11):1306-1309.in Chinese)
[16]赵坪锐.客运专线无碴轨道设计理论与方法研究[D].成都:西南交通大学,2008.
(ZHAO Pingrui.Research on the Design Theory and Method for Ballastless Track on Passenger Dedicated Line[D].Chengdu:Southwest Jiaotong University,2008.in Chinese)

