预应力混凝土梁精细化仿真分析关键问题研究

刘　杰，王海龙，张志国，张岩俊，卜建清

(1.石家庄铁道大学 土木工程学院，河北 石家庄　050043；2.西南交通大学 土木工程学院，四川 成都　610031;3.河北建筑工程学院 土木工程学院，河北 张家口　075000)

混凝土材料的力学行为表现出明显的非线性，其结构的破坏性分析以及安全性评价都应以非线性分析为基础[1]。随着预应力混凝土在公路、铁路等桥梁结构中的极大普及，对其在各种情况下的检测、监测、加固及安全性评估等方面的科研课题也日益增多，相关研究均涉及混凝土、普通钢筋及预应力钢筋的非线性问题。

对预应力混凝土结构进行精细化分析，一般需要考虑材料准确本构模型的获取、预应力钢筋端部锚固区混凝土的处理、普通钢筋的布置、混凝土开裂压碎后的处理、加载方法及求解策略等几大问题。同时，在进行预应力混凝土非线性仿真分析时，还存在不易收敛、计算量大、需通过大量试算促进收敛等问题。其主要原因是混凝土单元开裂和压碎以及钢筋屈服后存在不平衡力，需不断进行计算和分配。通常采取调整荷载步和网格密度，适当放宽收敛条件等方法加速收敛。在结构接近破坏时，大量开裂、压碎、屈服单元的出现，使结构整体刚度矩阵病态性严重且出现负刚度，计算将无法收敛。在混凝土结构接近破坏时，不少学者采用弧长法作为一种加速求解收敛的方法。但弧长法虽能有效克服结构负刚度引起的求解困难，对求解极值点问题及下降段问题具有独到的优势，但将其应用于混凝土结构的材料非线性有限元分析却未取得预期的效果。究其原因，主要是算法不能有效处理由于混凝土开裂等因素引起的应变局部化问题，而且ANSYS中的弧长法将排斥NR法自适应下降等促进求解收敛的策略。

基于ANSYS进行预应力混凝土结构破坏分析时，目前常采用模型试验验证。模型试验根据实际结构按比例缩尺，但有些材料如钢绞线数量、普通钢筋(包括纵筋和箍筋)的数量和布置等都很难按实际结构依据相似理论进行模型设计，所获得的试验数据并不一定能真实反映实际结构的工作性能。因此，为进行预应力混凝土梁的精细化仿真分析并获取其极限荷载，进行足尺破坏试验是最为直接而有效的办法。

本文基于ANSYS软件进行三维实体精细化建模及非线性仿真分析，并通过1片30 m预应力混凝土足尺T梁的破坏试验，借助荷载—挠度试验曲线分析混凝土裂缝的扩展情况，得到利用ANSYS进行非线性求解极限承载力问题的有效控制策略。

1　足尺试验梁试验

1.1　试验梁概况

本文作者对1片30 m预制预应力混凝土T梁进行足尺试验。试验梁主要构造如图1所示(限于篇幅，此处未画普通钢筋构造)。混凝土采用C50高性能混凝土，普通钢筋采用HRB335，预应力钢筋采用抗拉强度标准值fpk=1 860 MPa、公称直径d=15.2 mm的低松弛高强度钢绞线，预应力钢束N1和N2采用6Φs15.2钢绞线，预应力钢束N3和N4采用7Φs15.2钢绞线，设计锚下控制应力为0.75fpk。

1.2　试验加载方案

加载方式如图2所示。根据最大弯矩设计值反推出对应的集中力，按P=2 000 kN设计加载装置。梁端与下部钢筋混凝土支墩通过钢板支承，钢板尺寸为50 cm×50 cm×2 cm，支墩截面尺寸90cm×90 cm，钢板居中，梁端与支墩外边平齐，两支座中心距梁端的距离均为50 cm。试验在梁场进行，试验现场如图3所示。

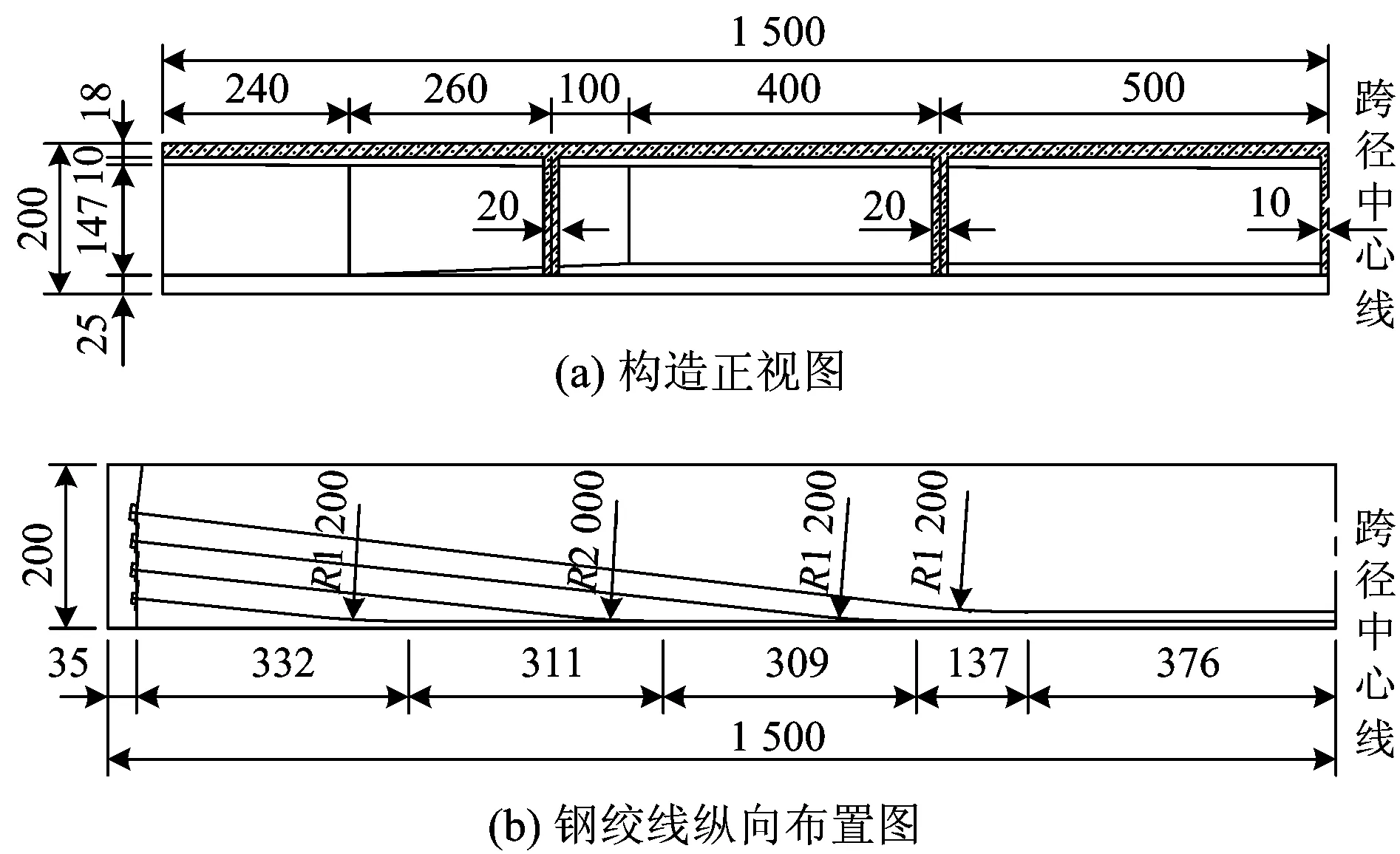
图1　试验梁构造图(单位：cm)

图2　试验梁加载布置图(单位：m)

图3　试验梁试验现场

采用全自动智能张拉加载系统逐级加载，先按100 kN级差进行加载，接近开裂荷载时改为按20 kN级差加载，接近极限荷载时改为按位移控制，按10 mm级差进行加载，以便获得下降段。

2　精细化仿真分析几个关键问题的处理

2.1　几何模型及端部锚固区混凝土的处理

创建几何模型时根据结构及受力的对称性，创建1/2几何模型。根据材料、几何外形关系以及配筋情况将全梁划分为等截面段、渐变段、梁端段以及横隔板部分。由于不同梁段的梁肋、板面、横隔板内的钢筋配筋情况不同，为实现精细化建模目的，首先对不同梁段按自底向上、由关键点创建面再拉伸成体的方式，然后通过工作平面在横隔板位置上对各梁段部分进行切分，最后采用自底向上的方法创建横隔板。

预应力混凝土梁中有些钢绞线属于空间曲线，创建其几何模型时，首先根据坐标创建相交直线，然后根据圆弧段半径并利用相交线倒角创建圆弧线。

预应力钢筋端部锚固区的混凝土应力场比较复杂，其截面应变的分布呈现明显的非线性特征，此处的处理直接影响混凝土结构仿真分析的准确性。为此，本文作者提出锚固区混凝土的一种处理方法，即建模时按照设计图纸中梁端部锚固区域的长度，利用工作平面对梁端部的40 cm区域进行切割，形成梁端部锚固区，将锚固区腹板部分的混凝土与主梁其他部分的混凝土分开，仅定义其材料属性为线性，以避免此处应力集中而过早开裂或压碎，从而影响整体结构的计算收敛性；但实际工程结构中此处由于增加了钢筋网片及钢垫板，足以保证此处不首先破坏，本文的试验过程也验证了这一点。

2.2　材料本构模型

混凝土结构有限元分析的最大难点在于本构模型的准确描述[2]。建模分析时若直接采用规范规定的材料数值，对梁的刚度会产生一定的影响。因此，通过测定混凝土实际强度，以获得混凝土材料的本构关系十分必要。本文通过测定14组随梁立方体试件的受压应力应变关系曲线，获得实际的混凝土材料本构；通过钢绞线的实际拉伸试验得到1860钢绞线的本构关系。

利用随梁试件测定混凝土强度等级，经统计分析判定混凝土材料强度等级为C55。

仿真时，混凝土采用MKIN多线性随动强化模型，该模型属于弹塑性模型，可以考虑混凝土的随动强化效应以及包辛格效应，适用于循环加载等，本构关系如图4所示。

图4　混凝土材料的本构关系

普通钢筋采用双线性随动强化模型BKIN模拟，该模型服从Mises屈服准则，考虑了包辛格效应。钢绞线采用MKIN多线性随动强化模型模拟。

2.3　单元选择及普通钢筋的布置

基于对混凝土非线性行为分析的目的，且考虑到实际结构中普通钢筋配置种类及数量多，故混凝土与普通钢筋采用ANSYS的3D加筋混凝土实体单元Solid65[3]模拟，该单元可以根据不同部位不同方向用实常数布置普通钢筋，且可以模拟混凝土材料的开裂和压碎行为。按计算的配筋率考虑普通钢筋的作用，其单元应力—应变关系矩阵D为

(1)

其中，

式中：Nr为钢筋材料序号；Vri为钢筋体积配筋率；Dc和Dri分别为混凝土和第i种钢筋的应力—应变关系矩阵；Eri为第i种钢筋的弹性模量；Ad为由方向余弦确定的向量，其具体表达式参见文献[3]。

如前2.1节所述，几何模型创建时划分了不同的区段，各区段普通钢筋在水平向(指纵筋)和竖向配筋率(指箍筋)不同。区域划分情况及各方向配筋率见表1。

钢绞线采用3D杆单元Link8模拟，该单元每个节点具有3个自由度，可承受轴向拉压。

划分Solid65单元网格时，对于试验梁的变截面段采用扫略法进行，其他部分采用映射法，单元尺寸取10 cm。

Link8单元尺寸为5 cm，直接划分网格，然后根据约束方程法对Link8单元节点与其附近多个Solid65单元节点建立约束方程，在Link8单元的1.25 cm内的Solid65单元建立约束。

表1　区域划分及配筋率情况

注：θ为钢筋在单元坐标系中xoy面的投影线与x轴的夹角；φ为钢筋与其在单元坐标系中xoy面投影线的夹角。

最后根据镜像分别对体和线单元进行复制镜像，形成整体结构的有限元模型。

2.4　混凝土开裂后的处理

混凝土开裂后应力的释放及剪力的传递问题一直是研究的热点问题[4-6]。为精细化模拟混凝土的非线性行为，需考虑混凝土的开裂和压碎行为，应根据不同的破坏模式调整应力—应变关系矩阵。

混凝土采用多轴应力状态的破坏准则，其判别式为

(2)

式中：F为主应力的状态函数；S为破坏状态分界面的数学表达式；fc为混凝土抗压强度。

当满足破坏准则时，表示混凝土压碎或者开裂。其中，若任一主应力为拉应力时，表示混凝土开裂；若所有主应力均为压应力时，表示混凝土被压碎。

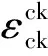
(3)

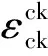
混凝土开裂后拉应力的释放按照缓慢释放处理，以防止刚度矩阵过早出现奇异，造成收敛困难。张开裂缝的剪力传递系数设置为0.5，裂缝闭合后剪力传递系数设置为0.95。

2.5　加载方法及求解策略

试验梁所受荷载包括自重、预应力和试验荷载3种。自重和预加力在荷载步1中一次施加。试验荷载在后续荷载步中施加，施加荷载方式采用按力和位移2种方式进行。施加荷载时为避免因泊松效应在与裂缝垂直的未开裂方向出现假压碎和假开裂现象，荷载增量步长要保证足够小。

进行非线性分析时，整体刚度矩阵中的元素不再是常数，而是随结构的应力和应变而变化[7-8]。因此，求解非线性方程组的方法大致可归结为3类：迭代法、增量法以及增量迭代混合法。ANSYS软件采用逐步递增载荷和平衡迭代的混合法进行求解。为保证计算精细化，平衡迭代时本文采用完全Newton-Raphson法，每一次平衡迭代均修改刚度矩阵，并利用自适应下降法加速收敛，迭代次数增大到500次，以使每一个载荷增量的末端解达到平衡收敛(在某个容限范围内)。

3　获得极限荷载及方法验证

利用第2节方法创建的试验梁有限元模型如图5所示，端部锚固区局部细节放大如图6所示。

为验证本文建模和设置方法的正确性，也为了得到获取仿真分析中预应力混凝土梁极限荷载的方法，本文进行了多种方案的比较验证，加载方式考虑力加载和位移加载，混凝土压碎开关考虑打开和关闭，收敛控制方法考虑按力和位移双控及仅位移控制，共有6种方案，具体见表2。

图5　试验梁有限元模型图

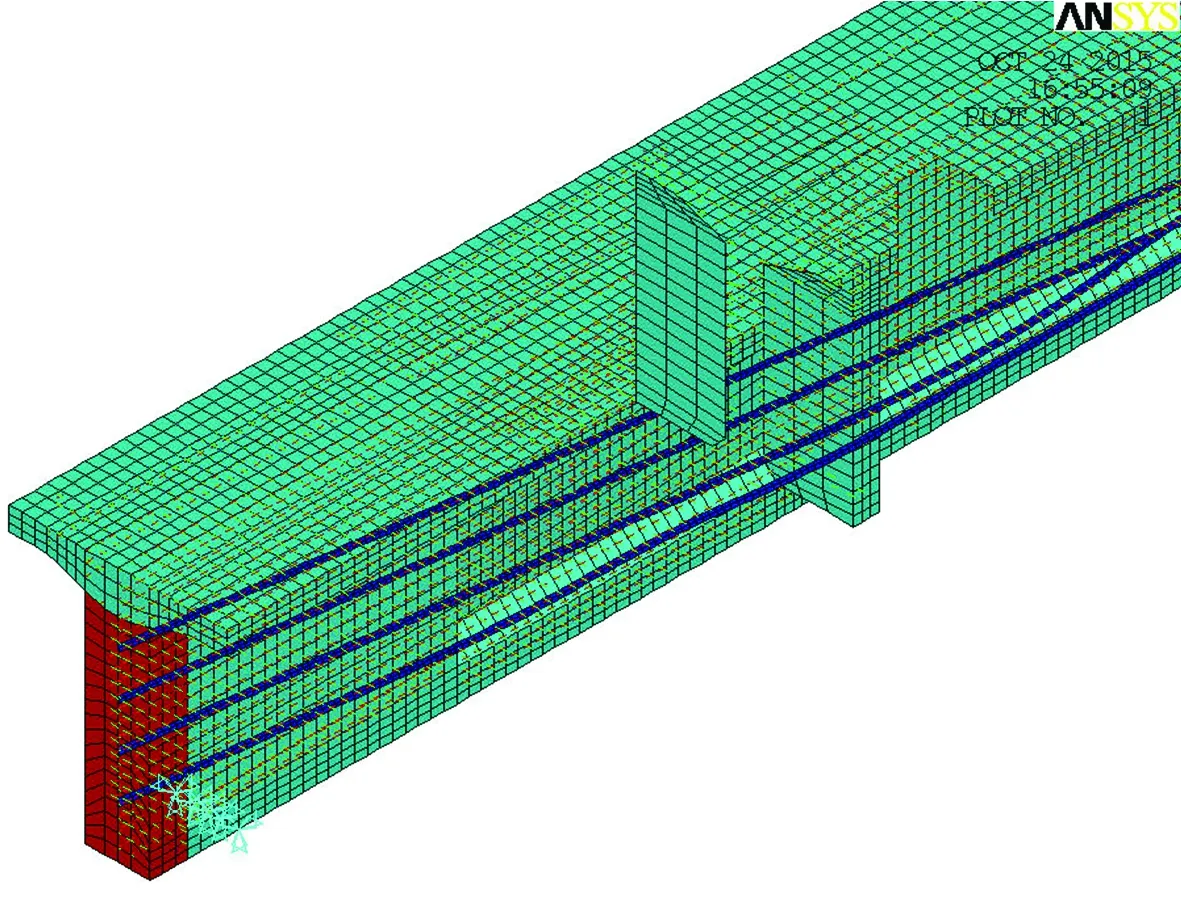
图6　端部锚固区细节图

方案加载方式混凝土压碎开关收敛控制方法1力加载　关闭力和位移控制2力加载　关闭位移控制　　3位移加载关闭力和位移控制4位移加载打开力和位移控制5位移加载打开位移控制　　6力加载　打开位移控制　　

混凝土压碎开关关闭情况下的计算结果与试验结果比较如图7所示。

图7　仿真计算与试验结果

由图7可知，关闭压碎开关且力加载时，仅采用位移控制及力和位移双控2种情况下，计算结果几乎一样。而位移控制比双控的计算速度快很多。因此，在计算混凝土结构非线性行为时，收敛控制采用位移控制即可满足要求。

由图7还可以看出，关闭压碎开关情况下，力加载和位移加载的结果并不一样，预应力钢筋屈服之前，计算结果一致；预应力钢筋屈服后，力加载比位移加载计算出的变形要小，位移加载更接近于试验值。

但在关闭压碎开关情况下，因ANSYS软件会在混凝土单元达到压碎状态后本构关系保持水平线，故仿真计算结果会以一定的斜率继续上升。因此，对于实际结构混凝土会压碎的情况，关闭压碎开关会导致无法模拟到极限荷载。

混凝土压碎开关打开情况下的计算结果与试验值对比如图8所示。

由图8可知，位移加载时，收敛控制方案选取力及位移双控(方案4)与仅采用位移控制(方案5)相比，在收敛情况下计算结果一致；但采用双控时，只能收敛到1 308.52 kN，之后便无法收敛，没有达到试验时的极限荷载1 490.9 kN；而仅采用位移控制时，可以最终收敛，超过荷载1 491.59 kN之后呈下降趋势，可以判定1 491.59 kN为仿真的极限荷载，其与试验极限荷载1 490.9 kN的误差仅为0.046%。因此，在计算混凝土结构的非线性行为时，采用位移控制即可满足要求。

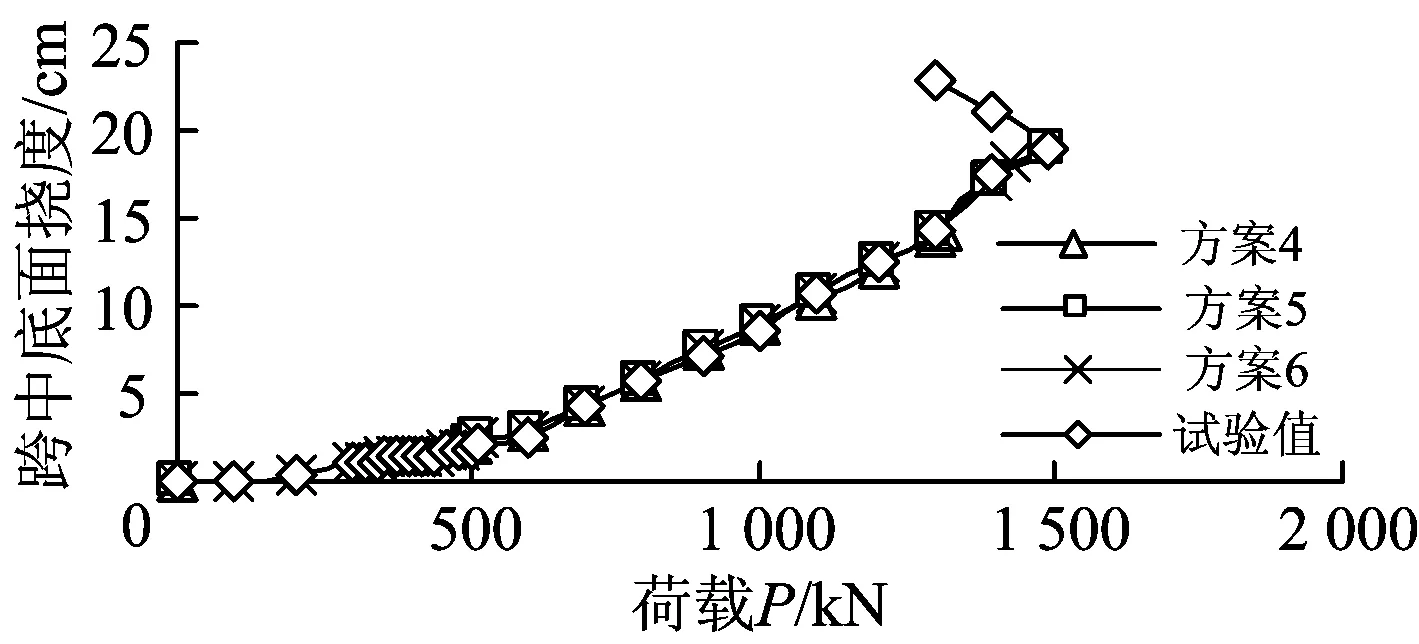
图8　仿真计算与试验结果

由图8还可知，在位移控制、力加载(方案6)时，只能收敛到1 434.803 kN，之后ANSYS软件提示不再收敛，其值与试验极限荷载1 490.9 kN的误差达到3.763%，其精度远远没有位移加载(方案5)高，若减小荷载子步的荷载值可逐步逼近极限荷载。故力加载与位移加载，在距极限荷载一定范围之前均可获得精确的仿真结果，但超过这个范围力加载时计算易过早发散，不易获得精确极限荷载。

另外，试验时跨中底边出现第1条裂缝时所对应的荷载为380 kN，但位移加载(方案5)时，虽然根据荷载步及子步的设置，每一子步设置为1 mm，由于ANSYS软件是直接将位移加至距水平面1 mm，即第1子步加载的位移为预拱度与1 mm之和，此时对应的支反力(相应荷载值)已经达到了450.01 kN，超过了开裂荷载。故力加载容易找到开裂荷载，而位移加载不容易找到开裂荷载。

本试验还对裂缝扩展情况做了记录，为节省篇幅，图9给出加载到1 000 kN时，试验梁跨中西南侧的裂缝情况，对应的仿真分析结果如图10所示。

图9　试验梁跨中西南侧裂缝图

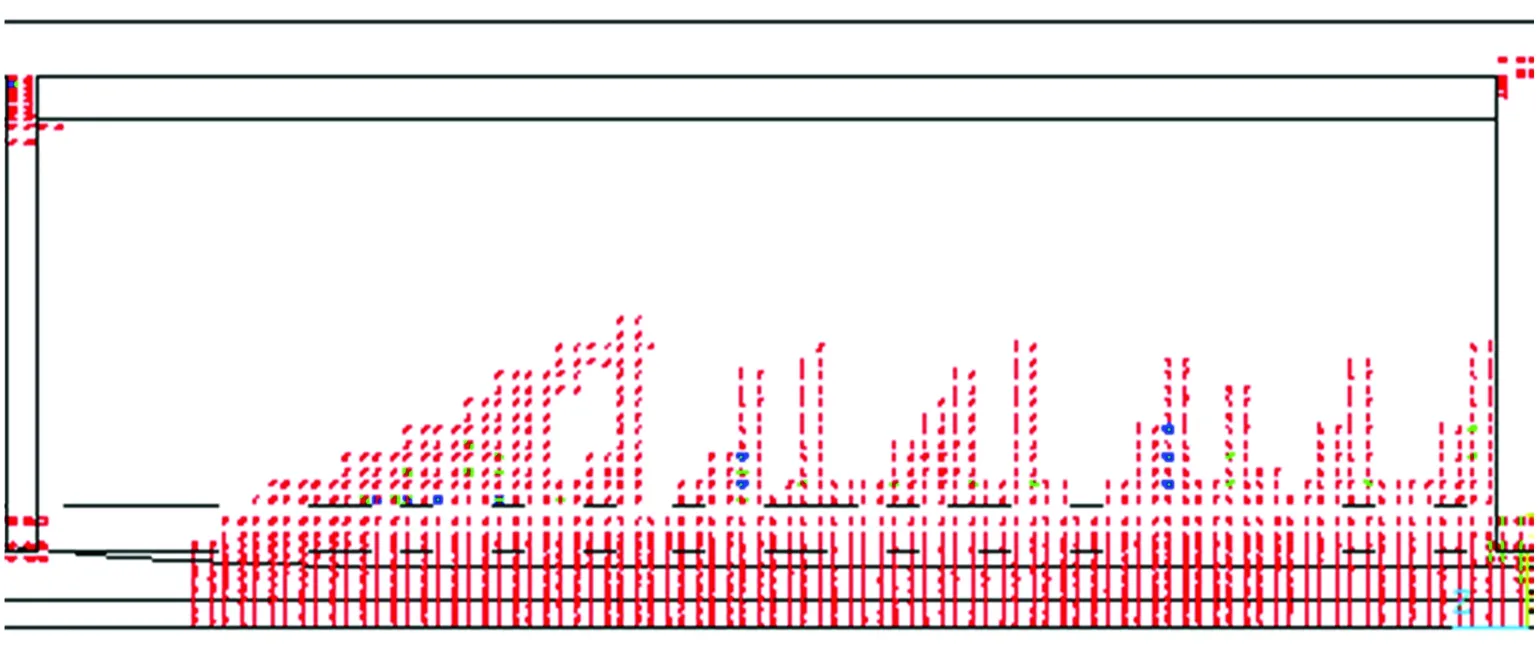
图10　试验梁跨中西南侧裂缝仿真图

根据现场试验，加载到800 kN时，中横隔板西侧出现6条裂缝，长度分别为106，114，138，100和116 cm，中横隔板东侧出现4条裂缝，长度分别为165，80，90和46 cm；加载到900 kN时，中横隔板西侧出现4条裂缝，长度分别为80，156，170和160 cm，中横隔板东侧出现5条裂缝，长度分别为54，136，46，90和50 cm；加载到1 000 kN时，向东第2横隔板中线起东侧出现5条裂缝，长度分别为116，145，150，140和86 cm，向西第2横隔板中线起西侧出现1条裂缝，长度为110 cm。仿真结果与试验情况基本吻合。

4　结　论

(1)提出梁端锚固区局部段混凝土模型的替代方法，即建模时结合设计图纸端部锚固区域长度，利用工作平面对端部区域进行切割形成端部锚固区，将锚固区腹板部分的混凝土与主梁其他部分区分开，仅定义其材料属性，以避免此处应力集中而过早开裂或压碎，影响整体结构的计算收敛性。

(2)利用Solid65单元，可以比较精确地模拟混凝土和普通钢筋的非线性行为。精细化分析时，需要分区段按纵筋和箍筋配筋率进行普通钢筋布置。

(3)在运用仿真分析求解预应力混凝土梁的极限荷载时，可在位移加载、打开压碎开关以及仅位移控制条件下进行。

(4)本文以试验梁为例进行精细化仿真分析及所得到的极限荷载求解方法适用于公路、铁路等预应力混凝土桥梁结构的仿真分析。

[1]刘军, 林皋. 适用于混凝土结构非线性分析的损伤本构模型研究[J]. 土木工程学报, 2012, 45(6): 50-56.

(LIU Jun, LIN Gao. Study of Damage Constitutive Model Applied to Simulate Nonlinear Behavior of Concrete Structures[J]. China Civil Engineering Journal, 2012, 45(6): 50-56. in Chinese)

[2]王勋文,潘家英. 按龄调整有效模量法中老化系数χ的取值问题[J]. 中国铁道科学, 1996, 17(3): 12-23.

(WANG Xunwen, PAN Jiaying. Evaluating Aging Coefficient χ in Age-Adjusted Effective Modulus Method[J]. China Railway Science, 1996, 17(3): 12-23. in Chinese)

[3]王新敏, 李义强, 许宏伟. ANSYS结构分析单元与应用[M]. 北京：人民交通出版社, 2011.

[4]KIM J J, TAHA M M R, NOH H C, et al. Reliability Analysis to Resolve Difficulty in Choosing from Alternative Deflection Models of RC Beams[J]. Mechanical Systems and Signal Processing, 2013, 37(1): 240-252.

[5]SOWIK M, NOWICKI T. The Analysis of Diagonal Crack Propagation in Concrete Beams[J]. Computational Materials Science, 2012, 52(1): 261-267.

[6]ISKHAKOV I, RIBAKOV Y. Exact Solution of Shear Problem for Inclined Cracked Bending Reinforced Concrete Elements [J]. Materials & Design, 2014, 57(5): 472-478.

[7]TIKKA T K, MIRZA S A. Nonlinear EI Equation for Slender Reinforced Concrete Columns[J]. ACI Structural Journal, 2005, 102(6): 839-848.

[8]YALCIN C, SAATCIOGLU M. Inelastic Analysis of Reinforced Concrete Columns[J]. Computers & Structures, 2000, 77(5): 539-555.