30 t轴重下重载铁路隧道基底结构的应力分布及动力响应
邹文浩,张 梅,刘艳青,马伟斌
(1.中国铁道科学研究院,北京 100081;2.蒙西华中铁路股份有限公司,北京 100070;3.铁科院(北京)工程咨询有限公司,北京 100081;4.中国铁道科学研究院 铁道建筑研究所,北京 100081)
当前,世界铁路发展呈现出两大趋势,即客运高速和货运重载。其中重载铁路是指行驶列车的总重大、轴重大或行车密度和运量特大的铁路,20世纪20年代美国建造首条重载铁路。60年代以后因其运能大、效率高、运输成本低等优点受到世界多个国家铁路部门的广泛重视[1]。美国、加拿大、巴西、澳大利亚、南非等幅员辽阔、煤炭和矿石资源丰富、大宗货物运量比重大的国家,均在发展重载铁路,大量开行重载列车。此外,在欧洲以客运为主的客货混运干线上也开始开行重载列车[2]。我国目前已有大秦铁路、朔黄铁路和瓦日铁路等多条重载铁路,为了满足重载铁路快速发展的需要,重载铁路的货车轴重须由目前主流的25 t提高至30 t,甚至更高。
货车轴重的提高和列车编组长度的增加,相应增加了隧道结构上的作用力和作用频度,使得隧道结构的受力、变形以及动力性能发生变化[3]。截止到2016年1月份,全路隧道病害率为48.78%,而重载铁路隧道病害率的不完全统计结果为76.83%,重载铁路隧道的病害情况比其他铁路隧道更为严重。
隧道基底结构直接承受列车荷载的作用,受重载列车荷载的影响最大,更容易出现病害。隧道基底病害发生后,如不及时处理,线路“带病”运营将会导致隧道基底结构开裂、破损等病害向上部衬砌结构发展,致使上部衬砌结构发生开裂、漏水等病害,结构的强度、刚度、稳定性等方面的安全储备下降,这些病害不同程度地恶化行车条件,限制行车速度,危及行车安全,缩短隧道维护周期和使用寿命,并制约铁路安全高效服役。隧道基底结构不仅是隧道结构病害的高发区域,还是隧道上部衬砌结构发生病害的主要诱因之一。因此针对重载铁路隧道基底结构在大轴重动载作用下的动力响应进行深入研究十分必要。
近年来已有一些学者对重载铁路隧道基底结构的动力特性开展了研究。尹成斐等[4]以朔黄铁路三家村隧道为工点进行现场测试,研究隧底填充层在动载作用下的动力响应和振动特性,并通过有限元计算分析隧底填充层、仰拱、拱腰和边墙等部位在动载作用下的动应力情况。扶晓康[5]基于已有重载铁路隧道的设计参数,通过有限元计算分析了重载铁路隧道基底结构各部位的动力响应特性,并研究了仰拱矢跨比、填充层厚度等设计参数和围岩软化、基底脱空等环境因素对隧底结构动力响应的影响。薛继连[6]针对朔黄铁路某隧道隧底不密实病害,对该病害的成因进行了分析,提出了采用聚氨酯树脂浆液对隧底不密实处进行填充并固结虚砟的加固方案,并采用有限元计算对该方案的加固效果进行了分析。李自强等[7]以瓦日铁路太行山隧道为工点进行了现场实测,研究轴重为27 t的重载列车经过时基底结构的动压力状况,并采用数值计算方法分析隧道基底仰拱等部位动压力的横向和竖向分布规律,最后对比分析了数值计算和实测结果。上述研究基本以数值计算为主要研究方法,而现场实测主要针对设计标准偏低的既有线或轴重偏低的情况,且数值计算模型多为严格按照设计参数构建的理想化模型,没有考虑现场施工方面的因素以及现场实际有较大偏差的情况。
鉴于此,本文以某重载铁路隧道为依托开展现场测试和数值模拟,研究30 t轴重列车荷载作用下重载铁路隧道基底结构的应力分布和动力响应,并通过数值模拟方法对目前由仰拱不同施工水平形成的3种主要基底结构形态进行施工时隧道基底结构受力状态及运营时隧道基底结构动力响应的对比分析。
1 现场实测
测试工点为单洞双线隧道,全长4 852 m,所处地段地形起伏强烈、冲沟发育,衬砌结构为复合式衬砌,轨道形式为无砟轨道,在Ⅴ级围岩区域选择1个断面进行隧道基底结构的动应力监测。
1.1 监测方案
现场实车试验主要对30 t轴重列车动荷载作用下隧道基底结构的动应力进行测试,以掌握30 t轴重列车通过时隧道基底结构的动力响应。所有传感器均埋设在填充层中,测点布置如图1所示。

图1 重载铁路隧道动态测试横断面布置图
1.2 动应力监测结果
监测断面主要部位的垂向和水平向动应力测试结果见表1。位于重车线右轨正下方填充层顶部测点的垂向动应力典型时程曲线如图2所示,其动应力幅值为122.2 kPa。
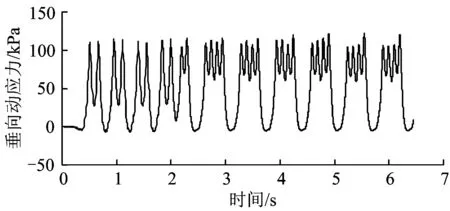
图2 垂向动应力典型时程曲线
由表1可见,填充层的垂向动应力均表现为压应力,沿隧道基底竖向出现较大幅度的衰减,填充层顶部的垂向动应力幅值远大于填充层底部;填充层顶部的水平向动应力为压应力,底部为拉应力,沿竖向出现由压至拉的转变;重车线正下方作为列车荷载作用的主要区域,其垂向和水平向动应力幅值均比其他位置大。
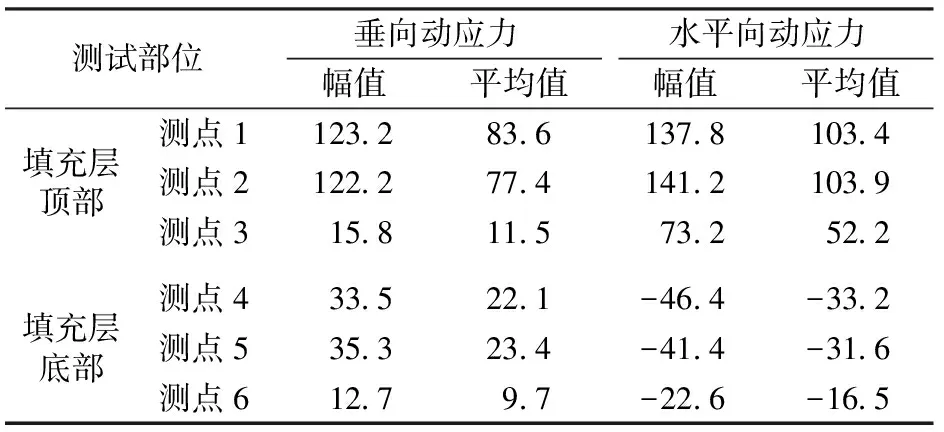
表1 垂向和水平向动应力测试结果 kPa
注:正值为压应力。
2 隧道结构动力响应数值模拟
采用有限差分程序FLAC3D建立隧道结构动力响应的三维数值分析模型,对动载作用下的隧道基底结构动力响应进行数值模拟,分析隧道基底结构各部位的动应力情况。
2.1 数值模拟
2.1.1隧道结构动力响应数值模型
建立的隧道结构动力响应数值模型如图3所示,模型沿隧道轴线方向取单位长度,宽度自隧道轴线向两侧各取40 m,高度自隧道轴线向上下各取40 m。
对于模型的边界条件,除模型顶面为自由边界外,模型四周和底部均采用静态边界。隧道结构和围岩均采用实体单元模拟,隧道结构和围岩间、仰拱和填充层间以及道床和填充层间均设置接触面以模拟层间接触特性。

图3 数值计算模型
围岩本构模型采用摩尔库伦模型,参数根据该隧道勘察设计资料并参考类似地层选取;隧道结构的仰拱、填充层、初支、二衬等各部位均采用线弹性模型,混凝土力学性能参数按照TB 10003—2005《铁路隧道设计规范》取值,有配筋的结构对钢筋进行等效处理,具体参数见表2。

表2 材料的物理力学参数
2.1.2列车动荷载模拟方法
列车动荷载的模拟应考虑的影响因素有列车轴重、悬挂质量、行车速度和线路平顺情况等,较为复杂。常用的模拟方法大致有现场测试法、人工模拟激励法和列车—轨道耦合模型法。现场测试法受载重、车速、轨道状态等因素影响,得到的测试结果离散性较大,较难用表达式准确描述,只能对特定工况进行分析;列车—轨道耦合模型法通过假定的轮轨接触关系连接列车模型和轨道模型,考虑较全面,但模型和参数过于复杂,且轮轨接触关系不够明确,计算效率较差;人工模拟激励法采用1个由经验公式拟合的激励力函数模拟列车荷载,可全面考虑轴重、车速等因素的影响,形式也较简洁,目前应用广泛。
本文采用文献[8]所述的激振力函数对重载列车荷载进行模拟,激振力函数包括静荷载和反映不平顺、轨面波形磨耗效应等因素的动荷载,并考虑了列车轮对力的叠加组合和钢轨、轨枕的分散传递,激振力函数如下。
F(t)=k1k2[P0+P1sin(ω1t)+P2sin(ω2t)+P3sin(ω3t)]
(1)
其中,
Pi=maiωii=1,2,3
ωi=2πv/Li
式中:P0为车轮静载;P1,P2和P3分别为与不平顺性、动力附加荷载和波形磨耗等相关的典型动荷载;k1为轮轨力叠加系数;k2为钢轨分散传递系数;m为列车簧下质量;ai为典型矢高;ωi为不平顺控制条件下的振动圆周率;v为列车行驶速度;Li为轨道几何不平顺波长管理值。
在列车轴重为30 t、运行速度为80 km·h-1的条件下,由式(1)计算得到的人工激振力时程曲线如图4所示,该荷载作用在Beam单元模拟的钢轨上。
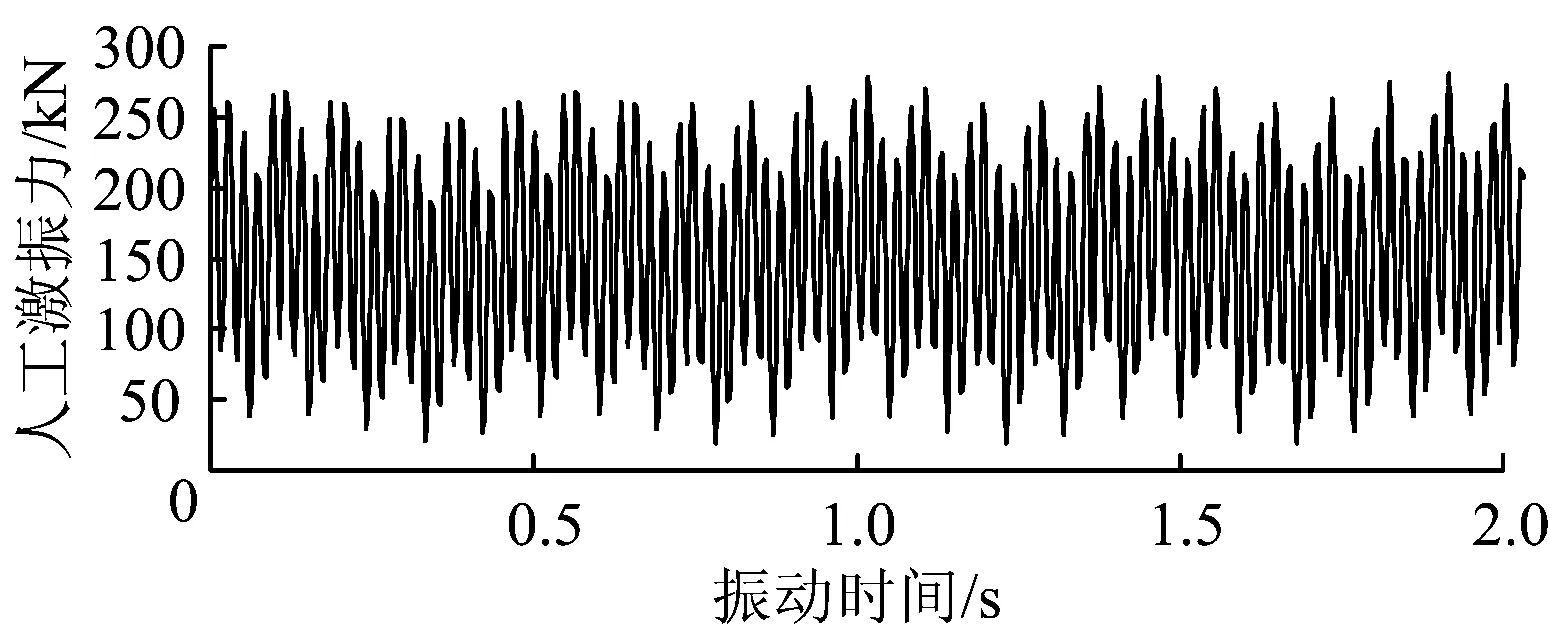
图4 根据列车动荷载模拟的人工激振力时程曲线
2.1.3数值模拟步骤
数值模拟的具体步骤如下。
(1)建立模型网格,赋予岩体参数,施加静力边界条件,然后生成初始地应力场。
(2)模拟开挖过程。全断面开挖后,地应力释放10%,施作初期支护后地应力释放20%,二衬施工后释放剩下的地应力,接着施加填充层和道床。
(3)设置动力边界条件,并施加人工激振力形式的重载列车荷载,同时在隧道基底结构关键部位设置监测点。
测点布置如图5所示。道床底部布置测点1和测点2,分别位于重车线右轨正下方和隧道中心线上;填充层底部布置测点3,测点4和测点5,分别位于重车线右轨正下方、隧道中心线上和空车线中心线上;仰拱底部布置测点6,测点7和测点8,分别位于重车线右轨正下方、隧道中心线上和空车线中心线上;沿重车线中心线布置1条竖向测线,以分析动应力的竖向传递。

图5 测点布置示意图
2.2 数值计算结果分析
2.2.1动应力
道床底部测点1和测点2的垂向及水平向动应力时程曲线分别如图6和图7所示。

图6 测点1和测点2的垂向动应力时程曲线
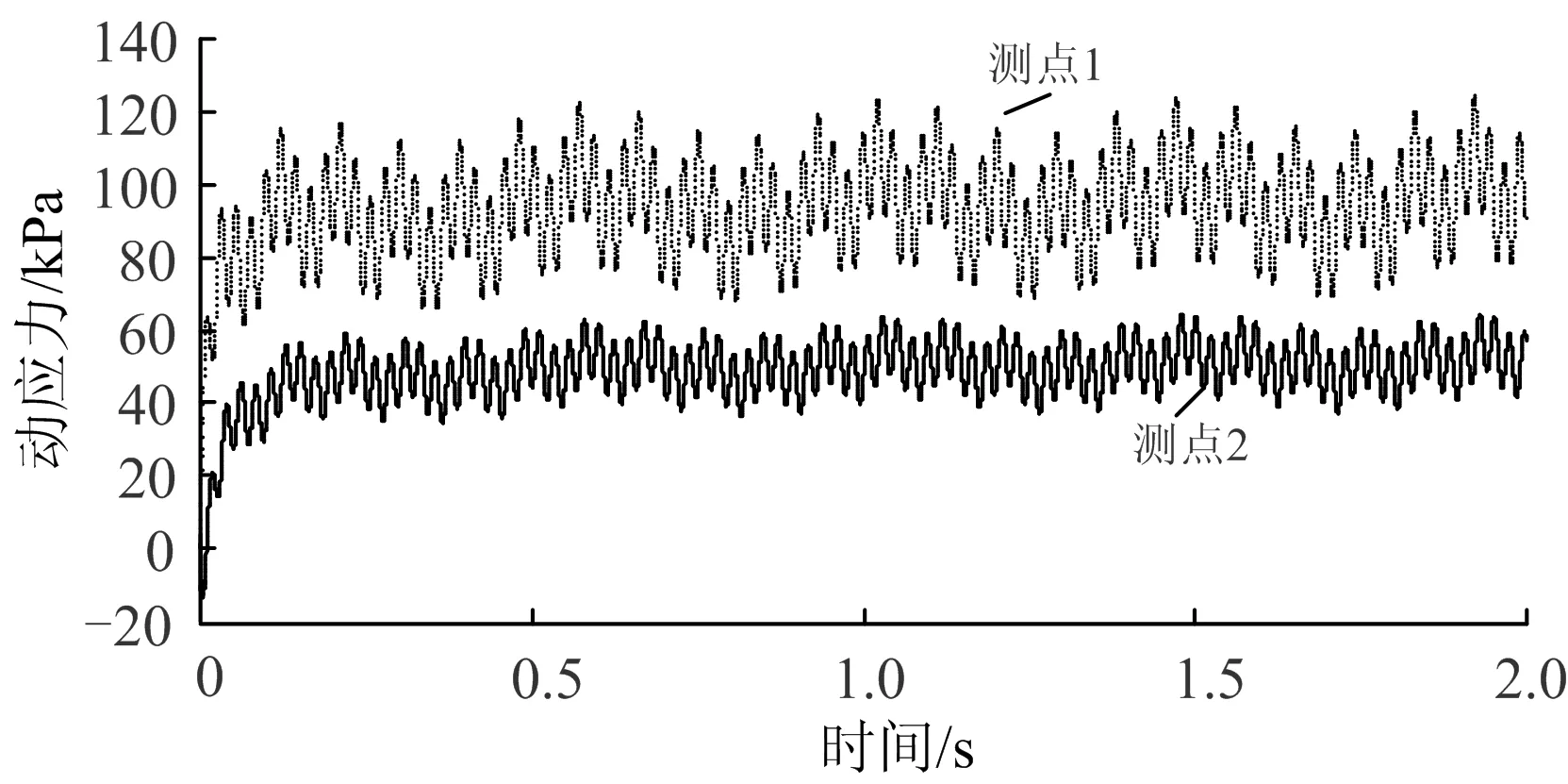
图7 测点1和测点2的水平向动应力时程曲线
由图6可见,测点1(重载线右轨正下方)和测点2(隧道中心线上)的垂向动应力幅值分别为120.8和1.1 kPa,均表现为压应力,道床垂向动应力在重车线轨道正下方的变化幅度较大。
由图7可见,在列车动荷载作用下,测点1和测点2的水平向动应力幅值分别为120.1和62.4 kPa,测点1的水平向动应力远大于测点2,两者均表现为压应力。
填充层底部测点3,测点4和测点5的垂向及水平向动应力时程曲线分别如图8和图9所示。
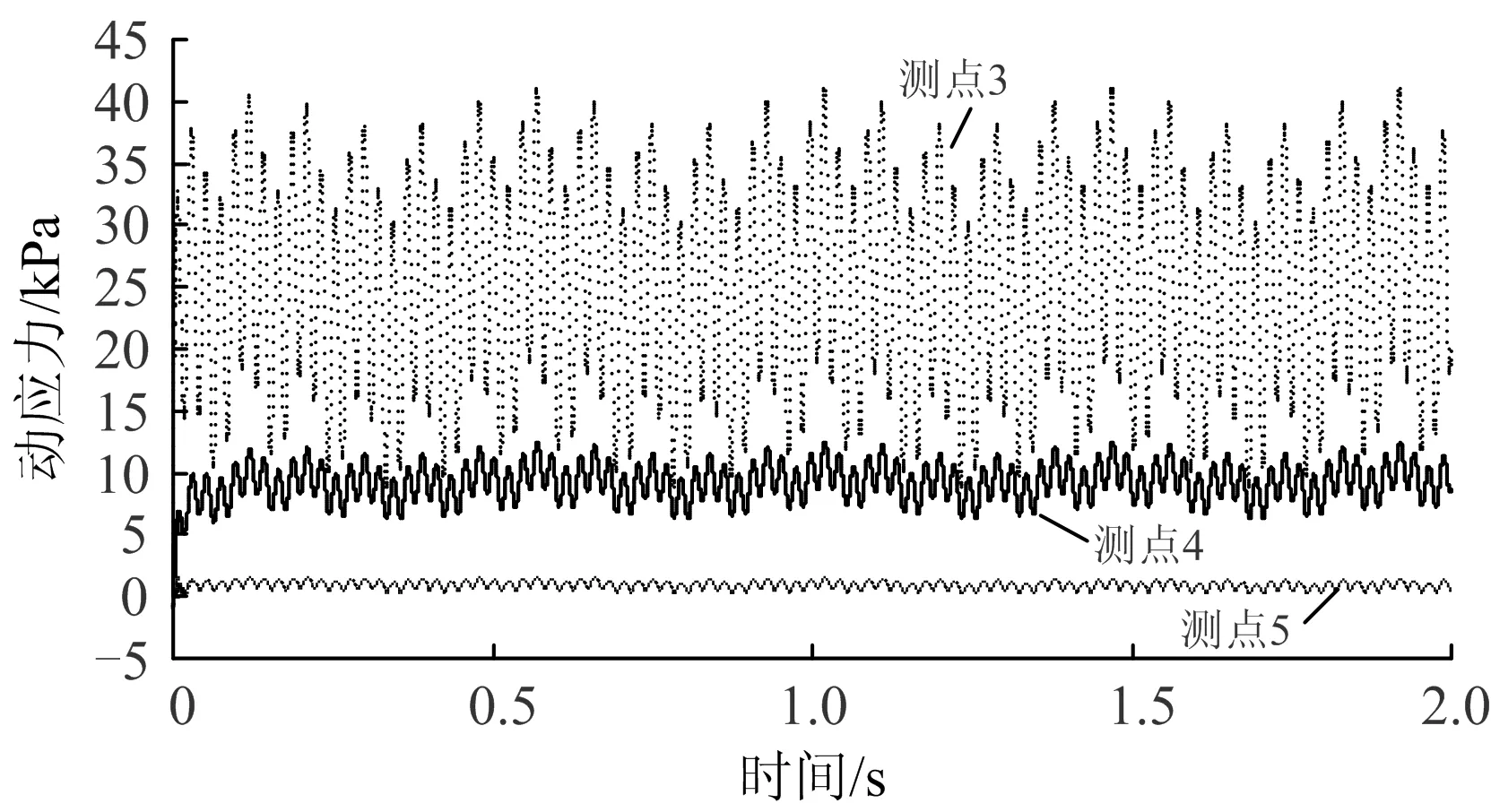
图8 测点3,测点4和测点5的垂向动应力时程曲线
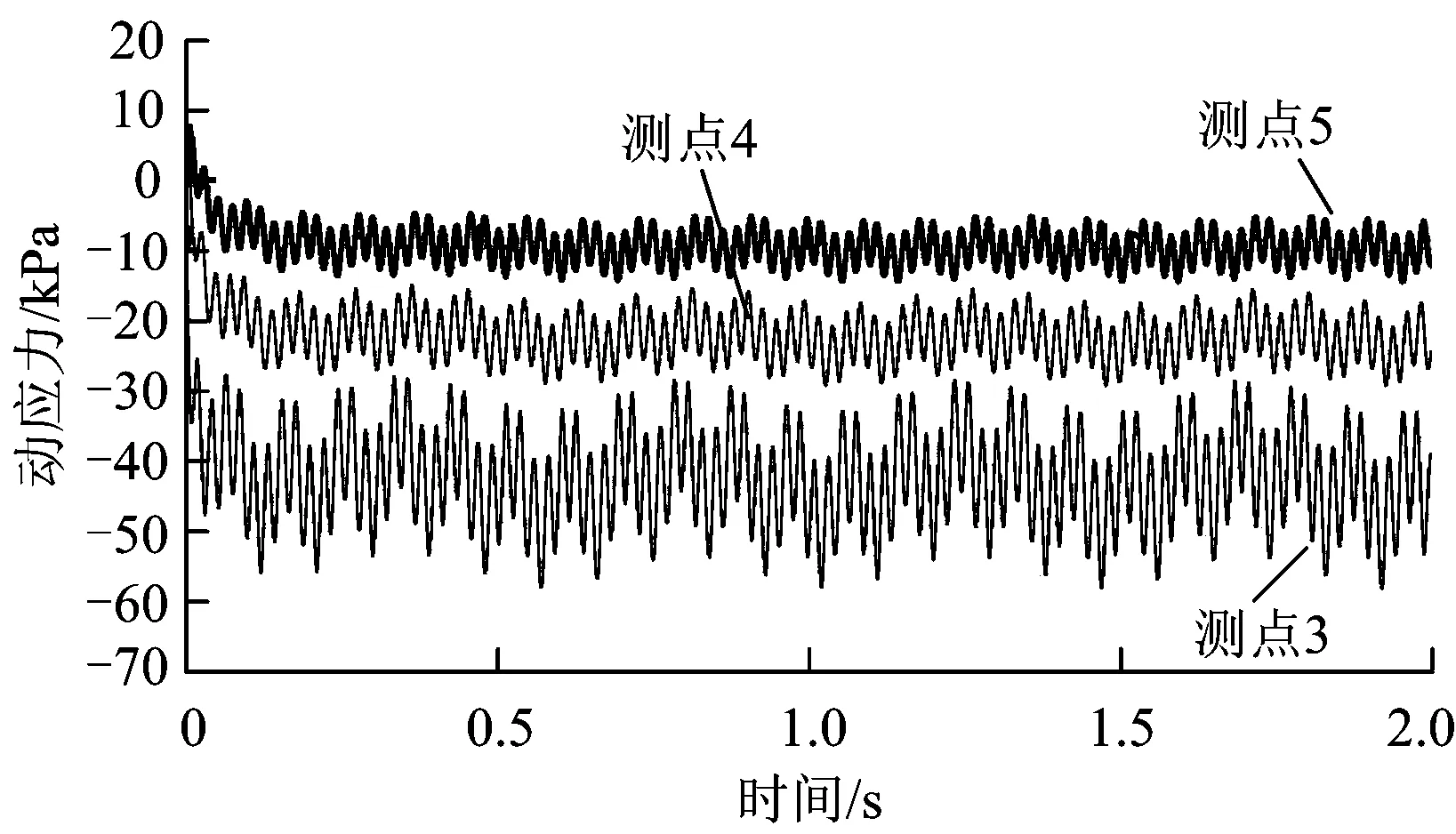
图9 测点3,测点4和测点5的水平向动应力时程曲线
由图8可知,测点3,测点4和测点5的垂向动应力幅值分别为40.0,12.2和1.5 kPa,均为压应力,填充层的垂向动应力在重车线线上变化较大,隧道中心线上次之,空车线线上较小。
填充层的垂向动应力与道床的相比,有一定程度的衰减。
由图9可知,在列车动荷载作用下,测点3,测点4和测点5的水平向动应力幅值依次减小,分别为-56.5,-26.1和-12.8 kPa,均表现为拉应力。
可见,填充层顶面的水平向动应力为压,底部为拉。
仰拱底部测点6,测点7和测点8的垂向及水平向动应力时程曲线分别如图10和图11所示。
由图10可知,测点6,测点7和测点8的垂向动应力幅值分别为25.8,12.5和2.0 kPa,均为压应力。
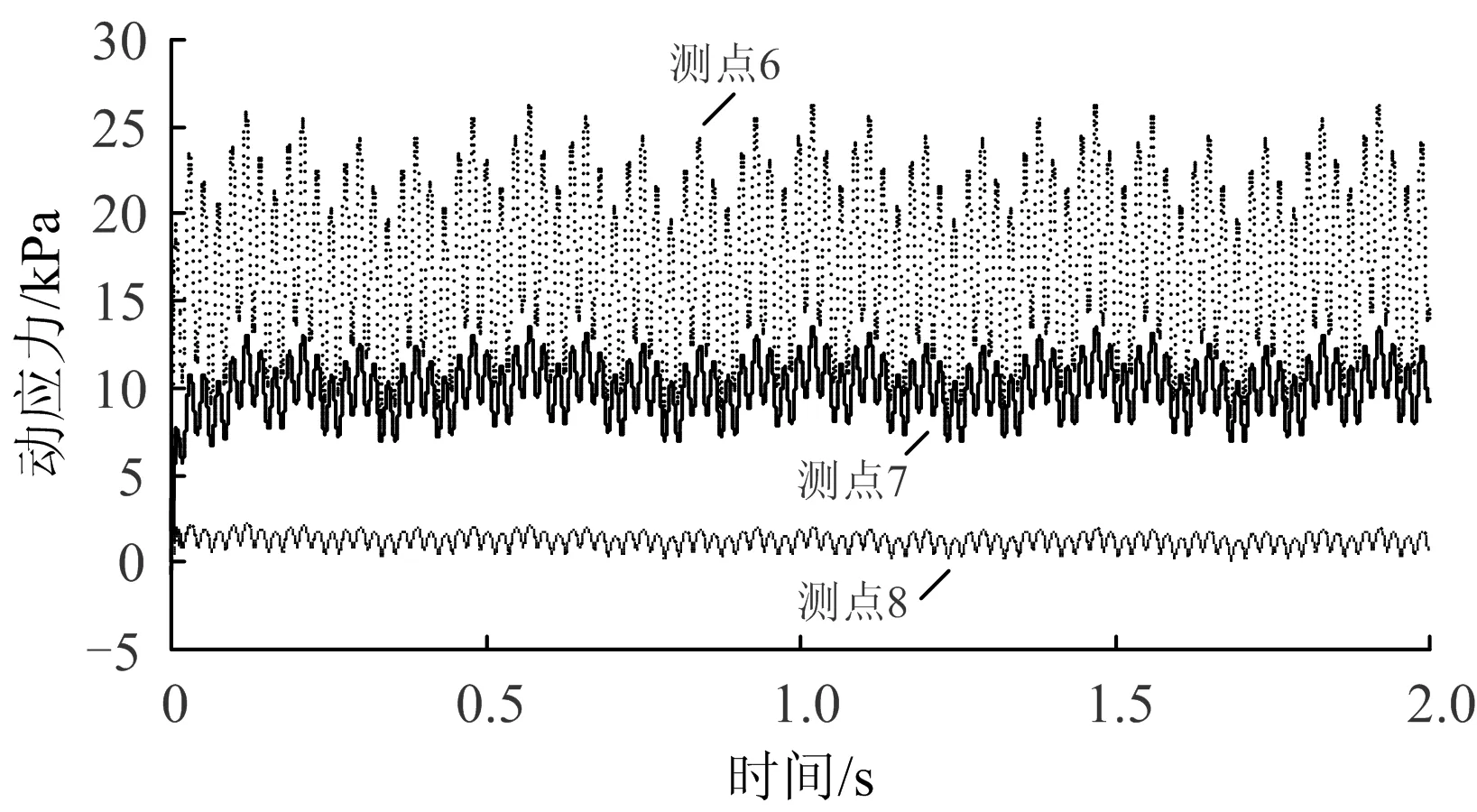
图10 测点6,测点7和测点8的垂向动应力时程曲线

图11 测点6,测点7和测点8的水平向动应力时程曲线
由图11可知,测点6,测点7和测点8的水平向动应力均为拉应力,幅值分别为-115.0,-56.1和-25.5 kPa,大于填充层底部相应位置的水平向动应力幅值。
图12为重车线右轨正下方垂向和水平向动应力幅值沿隧道基底竖向的分布情况。由图12可见:垂向动应力沿竖向呈逐渐衰减的趋势,以道床顶部动应力为基准,至道床底部的衰减率为23.2%,至填充层底部的衰减率为74.3%,至仰拱底部的衰减率为83.6%;水平向动应力沿竖向经历了由压到拉的变化,道床整体为压应力,填充层顶部为压应力,底部为拉应力;仰拱整体为拉应力,仰拱底部的拉应力较大。

图12 重车线正下方动应力幅值沿竖向分布情况
2.2.2与现场测试结果对比
数值模拟和现场实测得到的基底结构不同位置的垂向动应力见表3。由表3可见,除测点2外,其他测点垂向动应力的数值模拟结果与现场实测结果很接近。
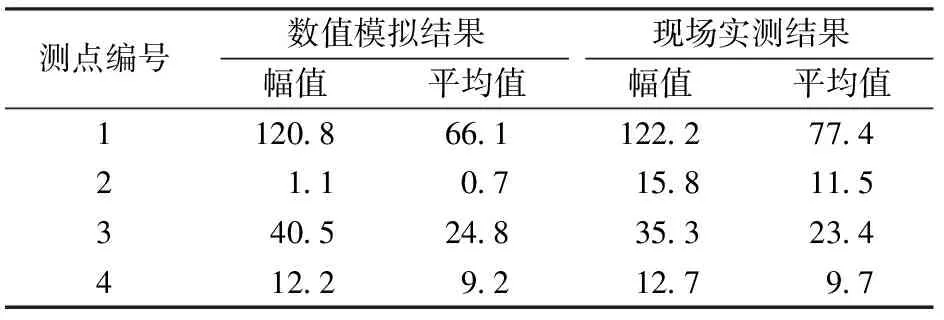
表3 垂向动应力结果对比 kPa
数值模拟和现场实测得到的基底结构不同位置的水平向动应力见表4。由表4可见,数值模拟结果与现场实测得到的填充层水平向动应力沿竖向的变化趋势相同,都为“上压下拉”,填充层顶部的水平向动压应力数值模拟结果偏小,填充层底部的水平向动拉应力数值模拟结果偏大。
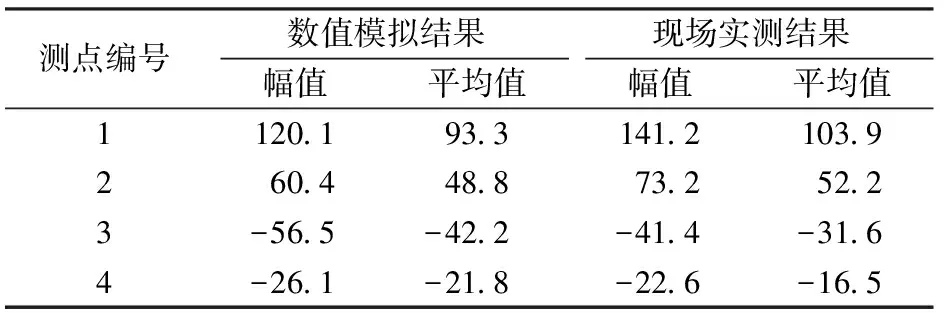
表4 水平向动应力结果对比 kPa
由于数值模拟的是较为理想化的工况,且考虑的影响因素具有局限性,故计算结果和现场测试结果稍有差别,但得到的隧道基底结构动应力结果基本能够反映重载列车荷载作用下隧道基底结构的动力特性。
3 不同隧底结构形态受力对比分析
上述现场实测和数值模拟分析的前提是假设现场施工严格按照设计要求。但是在实际施工中由于施工技术水平等因素的影响,成型后的隧道基底结构完全符合设计要求的很少,甚至有部分隧道基底结构建成后的形态与设计要求相去甚远。较为典型的是仰拱结构,通过现场调查和资料调研发现,目前仰拱施作后的典型断面形态主要有图13所示的3种类型。

图13 仰拱施作后的典型隧道断面形态
曲线型断面是较为理想的断面形态,仰拱矢跨比符合设计要求;折线型是实际施工中较为常见的断面形态,仰拱靠近墙角连接处的部分和设计接近,但填充层下方的区域曲率不够,较接近直线;直线型即仰拱施工之后矢跨比很小,基本上和直线接近。
3.1 对比计算相关情况介绍
针对上述3种隧道断面形态建立三维数值模型,分析隧道开挖过程中仰拱结构的受力状态及列车荷载作用下隧道基底结构的动力响应。三维数值模型如图14所示,模型参数和数值模拟步骤同第2章一致。
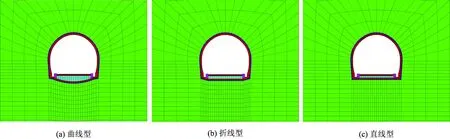
图14 不同断面形态的隧道结构三维数值模型
3.2 计算结果对比
3.2.1隧道基底结构受力状态
图15为不同隧道基底结构形态时二衬施作之后仰拱结构的水平向应力云图。由图15可见,曲线型断面时仰拱水平向应力基本都表现为压应力,最大拉应力仅为4.2 kPa;折线型断面时仰拱与边墙连接处及仰拱中心位置出现明显的水平向受拉情况,最大拉应力达51.3 kPa;直线型断面时同样在仰拱与边墙连接处及仰拱中心位置出现较大拉应力,最大值为86.6 kPa。直线型断面的仰拱受力状态最不利,折线型次之,曲线型最好。

图15 不同隧道基底形态下仰拱结构的水平向应力云图
3.2.2隧道基底结构动力响应
图16给出了在30 t轴重列车荷载作用下折线型和直线型隧道基底结构垂向动应力幅值沿竖向的分布情况,曲线型的情况见图12(a)。可以看出,隧道基底结构垂向动应力幅值都表现为压应力,且沿竖向呈现逐渐衰减的趋势。

图16 隧道基底结构垂向动应力幅值沿竖向分布情况
表5为不同隧道基底结构形态下垂向动应力沿隧底结构竖向衰减的情况。曲线型断面时的衰减率最高,折线型断面时仰拱底部的垂向动应力幅值比曲线型断面时高50.6%,直线型断面比曲线型断面高78.0%。直线型断面隧道基底基岩承受的垂向动应力最大,为47.3 kPa,折线型断面次之,曲线型断面最小。

表5 垂向动应力沿隧道基底结构竖向的衰减
4 结 论
(1)30 t轴重实车试验结果表明:在填充层顶部,重车线下方的垂向动应力较大,为123.2 kPa的压应力;沿隧道基底结构水平方向扩散,隧道中心线位置垂向动压应力变为15.8 kPa;沿隧道基底结构竖向出现明显衰减,填充层底部的垂向动应力约为25 kPa。填充层水平向动应力由上至下出现了由压至拉的转变,填充层顶部的水平向动应力为压应力,最大值为141.2 kPa,填充层底部的水平向动应力为拉应力,最大值为46.4 kPa。
(2)数值模拟得到的隧道基底结构动力响应结果和现场实测数据反映出来的趋势接近。数值计算结果表明:重车线下方道床顶部的垂向动应力超过150 kPa,至道床底部衰减为120.8 kPa,至填充层底部衰减为60.4 kPa,至仰拱底部衰减为25.8 kPa,衰减率为83.6%,都为压应力。水平向动应力在填充层中也表现为上压下拉,和实测结果一致,在道床位置均为压应力,在仰拱位置均为拉应力,仰拱底部的水平向动拉应力较大。
(3)数值模拟的工况较为理想化,且考虑的影响因素有限,结果和现场实测稍有差异,但基本能反映现场实测结果表现出的趋势。
(4)隧道二衬施作后曲线型断面时仰拱结构的水平向应力基本为压应力,最大拉应力仅为4.6 kPa;折线型断面时仰拱与边墙连接处及仰拱中心位置出现明显的水平向受拉情况,最大拉应力达51.3 kPa;直线型断面时同样在仰拱与边墙连接处及仰拱中心位置出现较大拉应力,最大值为86.6 kPa。直线型的受力状态最不利,折线型次之,曲线型最好。
(5)重载列车荷载作用下曲线型断面时沿隧道基底结构竖向的垂向动应力衰减效果最好,至仰拱底部的衰减率为83.6%;折线型断面次之,衰减率为77.3%;直线型断面最差,衰减率为70.8%。隧道基底结构的施工质量对隧道基底结构受力的影响很大,应密切关注。
[1]夏胜利,杨浩,张进川,等. 我国重载铁路发展模式研究[J]. 铁道运输与经济,2011,33(9):9-13.
[2]康熊,宣言. 我国重载铁路技术发展趋势[J]. 中国铁路,2013(6):1-5.
[3]王秀英,龚增进,刘维宁. 30 t轴重条件下隧道技术标准研究[J]. 铁道工程学报,2009(6):54-58.
(WANG Xiuying,GONG Zengjin,LIU Weining. Research on the Tunnel Technical Standard under 30 t Axis Load[J]. Journal of Railway Engineering Society,2009(6):54-58. in Chinese)
[4]尹成斐,付兵先,马伟斌. 重载列车作用下隧道结构的动应力分析[J]. 中国铁道科学,2013,34(3):47-52.
(YIN Chengfei,FU Bingxian, MA Weibin. Analysis on Dynamic Stress of Tunnel Structure under Heavy Haul Train[J]. China Railway Science,2013,34(3):47-52. in Chinese)
[5]扶晓康. 重载铁路隧道基底结构动力响应特性研究[D]. 长沙:中南大学,2014.
(FU Xiaokang. Study on the Dynamic Response Properties of the Foundation Structure in Heavy-Haul Railway Tunnel[D]. Changsha:Central South University,2014. in Chinese)
[6]薛继连. 30 t轴重下隧底密实度对隧底结构受力的影响及隧底加固效果分析[J]. 中国铁道科学,2015,36(1):90-95.
(XUE Jilian. Analysis of the Influence of Tunnel Bottom Compactness on Structure Stress and Strengthening Measures under 30 t Axle Load Train[J]. China Railway Science,2015,36(1):90-95. in Chinese)
[7]李自强,王明年,于丽,等. 重载铁路隧道基底结构的动压力响应[J]. 中国铁道科学,2016,37(1):71-77.
(LI Ziqiang,WANG Mingnian,YU Li,et al. Dynamic Pressure Response of Foundation Base Structure in Heavy Haul Railway Tunnel[J]. China Railway Science,2016,37(1):71-77. in Chinese)
[8]梁波,罗红,孙常新. 高速铁路振动荷载的模拟研究[J]. 铁道学报,2006,28(4):89-94.
(LIANG Bo,LUO Hong,SUN Changxin. Simulated Study on Vibration Load of High Speed Railway[J]. Journal of the China Railway Society,2006,28(4):89-94. in Chinese)

