一种适用于较少级联模块的H桥多电平变流器最近电平逼近调制改进算法

熊成林，张晓华，余　彬，刘　碧，张正松，冯晓云

(1. 西南交通大学 磁浮技术与磁浮列车教育部重点实验室, 四川 成都　610031；2.西南交通大学 电气工程学院，四川 成都　610031)

较之传统的两电平、三电平和多电平结构的变流器，级联型多电平变流器采用低压、低频器件实现高频、大功率的输出，具有很多优点：变流器子模块结构相同，其设计、安装和维修很容易实现模块化；变流器输出电压高、谐波含量低；电压变化率小，功率器件应力小、开关频率低等[1-2]。以级联H桥多电平变流器为代表的级联型拓扑则采用模块化的结构设计，便于系统扩容和引入冗余控制模式，在实际工业应用中较多采用这种结构。

脉冲调制技术是直接影响多电平变流器输出性能的关键技术之一。传统的脉冲调制技术包括脉宽调制(Pulse Width Modulation，PWM)技术、空间矢量脉宽调制 (Space Vector Pulse Width Modulation，SVPWM)技术、最近电平逼近调制(Nearest Level Modulation，NLM)技术等[3]。其中的NLM是一种实时调制方法，具有低次谐波含量少、开关频率低、开关损耗小、效率高、实现方式简单等优点，但既有NLM技术所采用的算法(简称NLM传统算法)只适合用于电平数为数十及以上的变流器[4-5]。相关学者研究了不对称级联多电平变流器在负载不变的情况下某些模块进入再生状态的问题[6]，以及新型电压平衡策略和NLM算法的改进[7]、NLM算法下的不同触发方式以及不同电平数和调制下的谐波特性[8]、三相级联多电平变流器相间环流的抑制[9]等问题。但这些研究均没有分析NLM传统算法本身的调制误差问题，而这种调制误差在中压应用领域、级联模块较少的情况下会对变流器的性能产生不利影响。

文献[10]提出了采用级联H桥多电平变流器的地面过电分相系统，用以解决传统地面过电分相装置存在的问题。该系统需要10个左右的H桥模块级联，采用NLM传统算法时存在较大的调制误差。因此，本文通过分析NLM传统算法中关于各级子模块、电压分辨率对变流器输出电压幅值和等效面积的影响，确定对变流器输出性能影响最大的因素，在此基础上提出NLM改进算法，并进行Matlab/Simulink仿真验证。

1　NLM传统算法

单相级联H桥多电平变流器电路结构如图1所示。图中：Ti1，Ti2，…，Ti4(i=1，2，…，n)为开关管，其中n为子模块的个数；Di1，Di2，…，Di4为二极管；Uc为子模块直流侧电压；uab1，uab2，…，uabn为各H桥子模块输出电压；uab为级联H桥多电平变流器的输出电压。

图1　单相级联H桥多电平变流器的电路结构

因为多电平变流器输出电压满足

(1)

所以，子模块数量为n个的H桥多电平变流器整体的工作状态共有n3种，其中输出端电压uab共有2n+1种有效状态。

NLM传统算法的基本思想是：当级联多电平变流器的电平数足够多时，可以使用阶梯波通过瞬时电平叠加对调制波直接进行逼近，而不需要采用脉宽控制的方法。图2为级联数是5个的级联H桥多电平变流器采用NLM传统算法时的电压调制示意图。图中：uabr为调制电压；θ1，θ2，…，θ5为各子模块状态转换的角度。

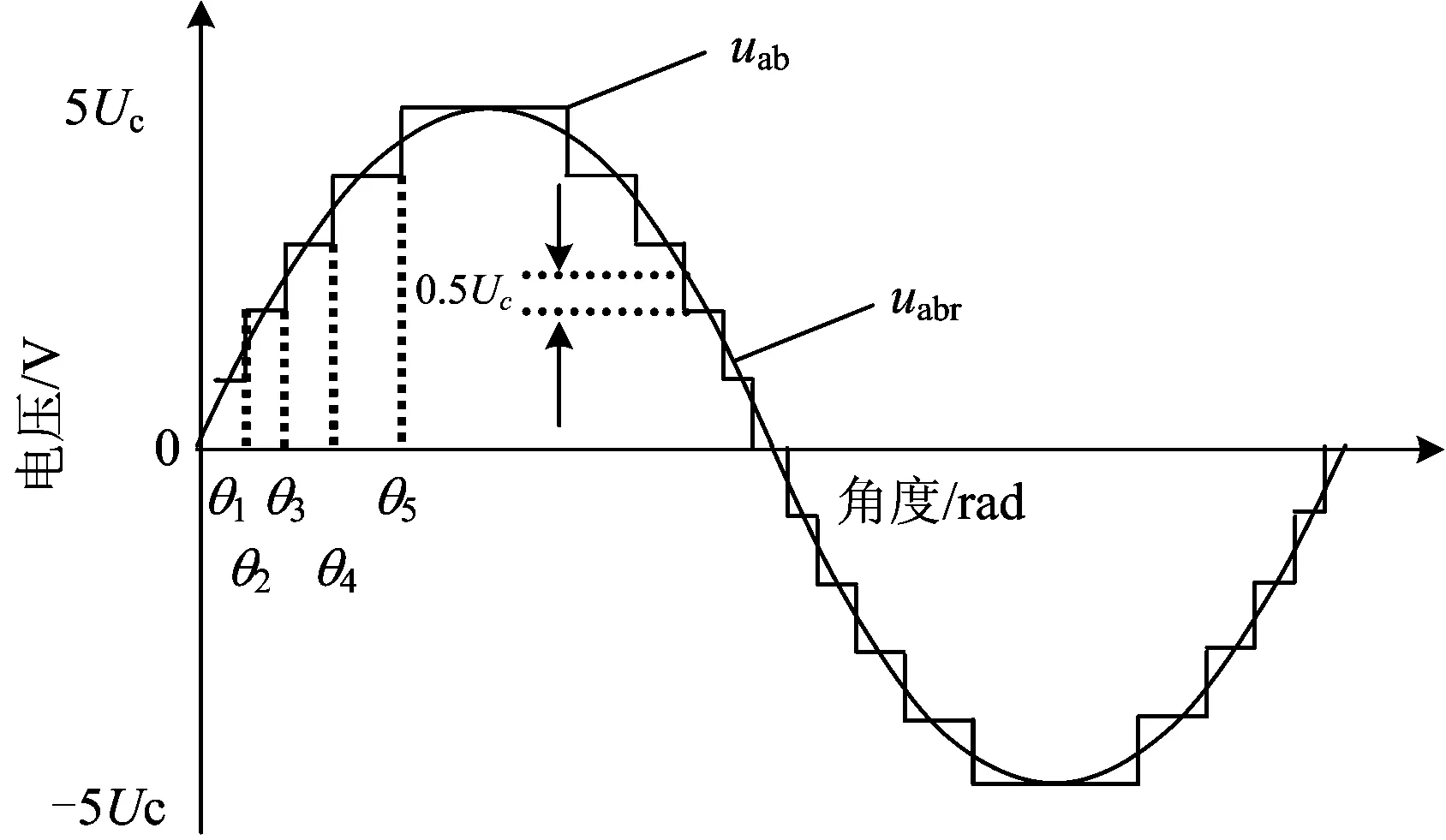
图2　采用NLM传统算法时的电压调制示意图

根据NLM传统算法，在各个电平转换时刻θ1,θ2，…，θi需要投入的子模块数量为

(2)

式中：na为需要投入的子模块数量；round(x)为取与x最接近的整数。

当na>0时，表示有数量为na的子模块以输出电压幅值为Uc的状态投入工作；na<0时，表示有数量为na的子模块以输出电压幅值为-Uc的状态投入工作。由于正弦波形的对称性，因此只需要分析1/4周期的调制即可。

各子模块投入工作的时刻可以采用下式计算。

(3)

式中：uabrm为调制电压的幅值。

各子模块对应的正弦调制时刻θisin为

(4)

2　NLM传统算法调制特性对变流器输出性能的影响

理想情况下，调制电压幅值uabrm为子模块直流电压Uc的整数倍，因此调制电压幅值不存在误差。此时，每个子模块投入工作时的等效面积特性如图3所示。图中：Sisin为第i个子模块投入工作时对应的标准正弦电压波面积；SiNLM为采用NLM传统算法时第i个子模块投入工作对应的输出电压波等效面积。

由图3可见，

(5)

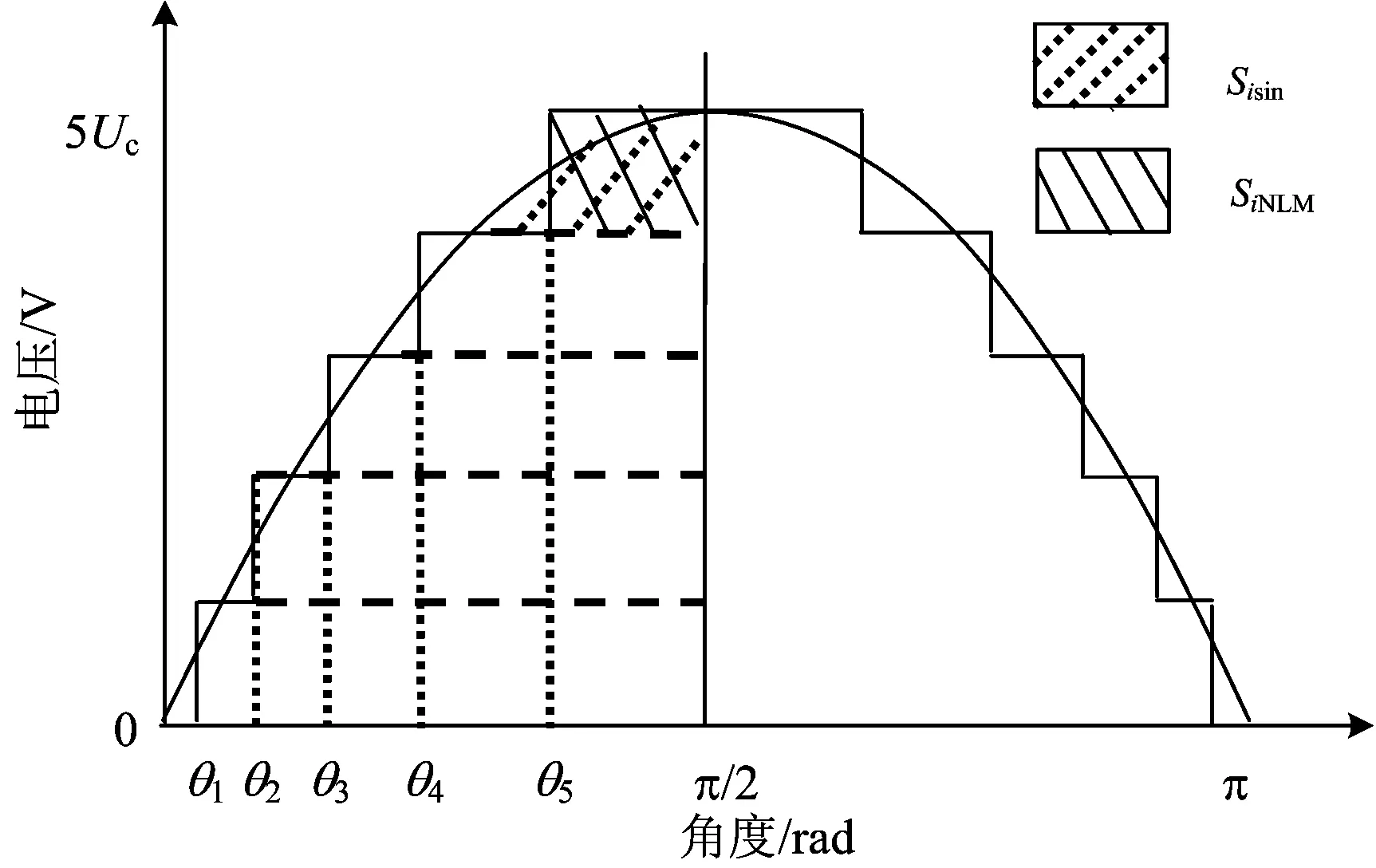
图3　采用NLM传统算法时的等效面积特性

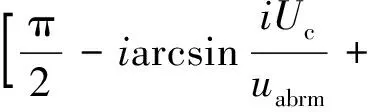
(6)

以uabrm为基准并进行标准化，则根据式(5)和式(6)可以计算出当uabrm为Uc的整数倍且子模块数为8～14时，各个子模块投入工作时变流器的输出电压波等效面积与对应的标准正弦电压波面积的误差百分比ei如图4所示，最后一级子模块投入工作时产生的面积误差百分比eiL如图5所示。

图4　不同子模块投入工作时产生的等效面积误差百分比

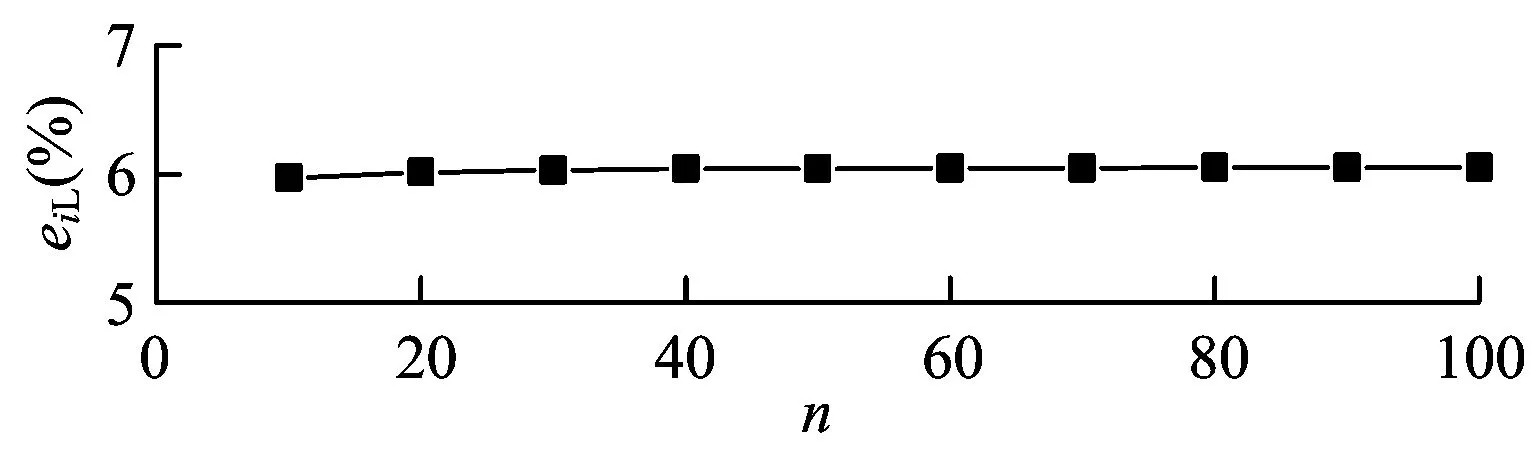
图5最后一级子模块投入工作时产生的等效面积误差百分比

从图4和图5可以看出：当调制电压幅值为Uc的整数倍时，非峰值附近投入工作的子模块产生的等效面积误差均小于0.5%；峰值附近模块产生的等效面积误差都较大，在5.95%～6.06%之间。

NLM传统算法的电压分辨率为0.5Uc，如果调制电压的峰值不是子模块电压的整数倍时，将会产生较大的误差，则由电压分辨率产生的最大调制电压幅值误差ea为

(7)

式中：namax为需要投入的最大模块数量，namax≤n。

对应的正弦电压波等效面积误差es为

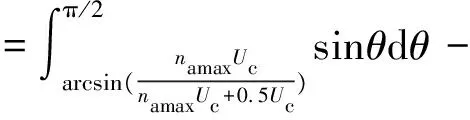
(8)

由电压分辨率产生的最大调制电压幅值误差和正弦电压波等效面积误差如图6所示。

图6　分辨率引起的幅值误差和等效面积误差

从图6可以看出：在子模块数量小于20个时，由NLM传统算法电压分辨率引起的最大幅值误差大于2.5%，最大等效面积误差大于0.36%。

下面以级联H桥多电平变流器并网运行为例，分析NLM传统算法的调制特性对变流器性能的影响。

针对文献[10]提出的新型地面过电分相系统，图7给出了变流器并网后的等效电路。图中：uml∠φl(l=A或B)为接触网供电臂降压变压器输出端电压，其幅值为uml，夹角为φl；umLl∠φLl为供电臂负载端电压，其幅值为umLl，夹角为φLl；uabm∠φc为变流器输出电压，其幅值为uabm，夹角为φc；umLc∠φLc为变流器并联端电压，其幅值为umLc，夹角为φLc；r1和rl为线路的等效电阻；X1和Xl为电路的等效电抗；XL和rL分别为负载的等效电抗和等效电阻；j为虚部。

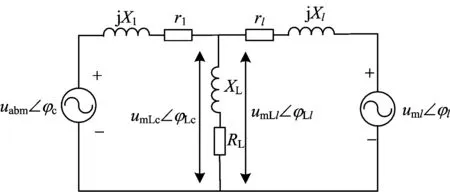
图7　变流器并网的等效电路

变流器输出的视在功率S1为

S1=P1+jQ1=U1I1

(9)

式中：P1和Q1分别为变流器输出的有功功率、无功功率；U1和I1分别为变流器输出的电压矢量、电流矢量。

变流器输出的电流为

(10)

故

S1=uabm(cosφc+jsinφc)×

(11)

则变流器输出的有功功率和无功功率分别为

(12)

在分析NLM传统算法对变流器的影响时，φc，φLc，r1和X1均可认为是定值。由前文分析可知，NLM传统算法以开关管的开关频率为基波频率，通过控制系统能够实时调整变流器的调制电压，但是会导致变流器输出电压波的等效面积产生误差，也即会对变流器输出电压uabm的大小产生影响。由式(12)可知，变流器输出电压uabm偏离参考电压时，变流器输出的有功功率P1和无功功率Q1均会偏离给定值，从而导致：①变流器在给定的功率发生变化时，会延长其动态响应时间，弱化变流器的动态跟踪性能；②稳态时，变流器输出功率波动增大。

3　NLM改进算法

3.1　基本思想

NLM改进算法的基本思想是：利用面积等效，通过对调制电压幅值附近正弦电压波的面积计算，确定对应子模块的作用时间。

定义电压幅值误差ΔUsm为

ΔUsm=|uabrm-nUc|

(13)

由于NLM传统算法的最大电压分辨率为0.5Uc，因此NLM改进算法分为2种情况。

1)ΔUsm<0.5Uc时

如图8所示，传统NLM算法将会削去ΔUsm对应的部分，从而产生调制误差。该情况下改进算法，则需要将ΔUsm对应的调制电压波的等效面积与上一区间对应的调制波面积求和，然后计算出对应子模块的作用时间。

图8　ΔUsm<0.5Uc时NLM改进算法示意图

2)ΔUsm≥0.5Uc时

如图9所示，传统NLM算法将会额外增大最后一级子模块作用时间，同样也会产生调制误差。改进算法则通过计算ΔUsm对应的正弦调制波面积，进而求出对应子模块的作用时间。

图9　ΔUsm≥0.5Uc时NLM改进算法示意图

3.2　实现步骤

NLM改进算法，可以通过如下步骤实现。

步骤1：初步确定需要级联的模块数量ni，将uabrm与Uc进行向下取整的除法运算。

(14)

步骤2：利用式(15)判断需要投入的最大模块数namax

(15)

步骤3：计算最后一级子模块对应的正弦电压波面积。

(16)

步骤4：计算最后一级子模块的作用时间。

最后一级子模块投入工作的时长Tlast为

Tnlast=namaxSnlast

(17)

则在[0,π/2]区间内，最后一级电平作用的时刻θlast为

(18)

NLM改进算法中各子模块开始作用的时刻为

(19)

3.3　影响分析

NLM改进算法的本质是利用面积等效，通过对变流器输出电压幅值附近正弦调制波的面积计算，确定对应子模块的作用时间，从而实现变流器输出电压高精度的跟踪调制。因此，算法改进后可以使变流器输出的有功功率和无功功率得到很好的跟踪控制，并减小系统的稳态波动。

此外，NLM改进算法调整了变流器输出电压峰值附近子模块投入工作的时刻，使输出电压波形偏离了标准正弦波形，因此会导致谐波含量增加。但由于NLM改进算法一般只应用于子模块相对较多的场合，输出电压幅值附近子模块投入工作的等效面积只占整个电压波面积的很小部分(namax≥8时输出电压幅值附近子模块投入工作的等效面积占比小于0.05%)，因此谐波含量的增加比例也非常小。

4　仿真验证

为了验证NLM改进算法，搭建了单相电源为负载供电的等效模型，如图10所示。图中：Us为电源；取X1=5.494 6 Ω，r1=2.00 Ω，XL=11.938 1 Ω，RL=92.00 Ω；Us分别为标准正弦电压、采用NLM传统算法调制后的变流器输出电压、采用NLM改进算法调制后的变流器输出电压，其中NLM传统算法和NLM改进算法采用的调制波均为标准正弦电压。

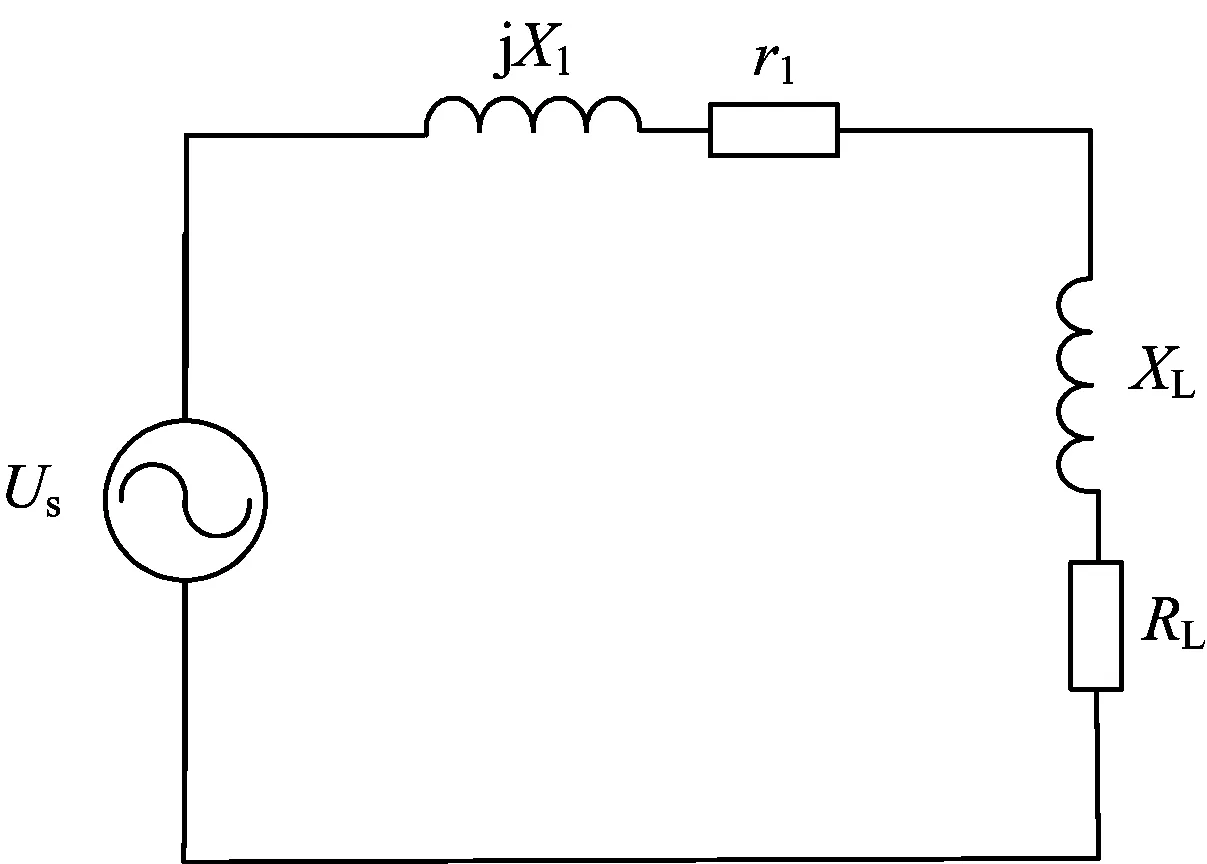
图10　单相电源为负载供电的等效模型

考虑到新型地面过电分相系统的正常工作范围，并且覆盖1个H桥级联单元子模块的直流电压为3 250 V，取标准正弦电压的最低幅值为32.4 kV，并按100 V幅值递增，最终增大至35.7 kV，对应的H桥子模块投入工作的最大级联模块个数为10～11，对应的交流电压有效值为22.910～25.244 kV。令标准正弦电压供电与采用NLM改进算法时变流器的输出有功功率误差为ΔPesi、与采用NLM传统算法时变流器的输出有功功率误差为ΔPesn，则电压幅值变化时，传统算法与改进算法的有功功率误差如图11所示。

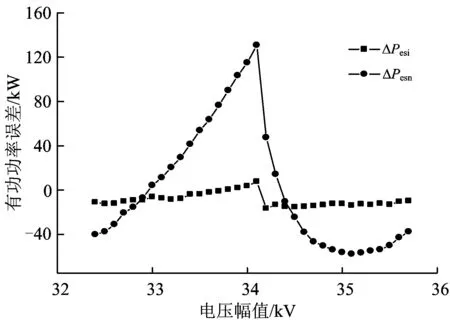
图11　电压幅值变化时有功功率误差

类似的，令标准正弦电压供电与采用NLM改进算法时变流器的输出无功功率误差为ΔQesi、与采用NLM传统算法时变流器的输出无功功率误差为ΔQesn，则电压幅值变化时，传统算法与改进算法的无功功率误差如图12所示。

图12　电压幅值变化时无功功率误差

由图11和图12可见：采用NLM改进算法时，无论是有功功率误差还是无功功率误差，均远远小于采用NLM传统算法时。

将图11和图12所示的有功功率误差和无功功率误差分别取绝对值并求和，可得采用NLM改进算法时的功率误差为NLM传统算法的20.93%。

令采用NLM改进算法时变流器输出电压的谐波含量为THD-INLM，采用NLM传统算法时为THD-NLM，则电压幅值变化时，2种调制算法下变流器输出电压的谐波含量如图13所示。

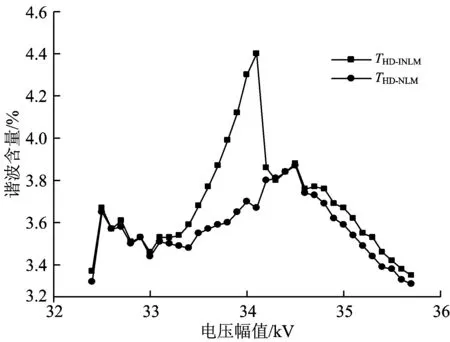
图13　电压幅值变化时2种调制算法输出的电压谐波含量

对图13所示的电压谐波含量进行求和计算， 可得采用NLM改进算法时的输出电压谐波含量仅比采用NLM传统算法时增加了3.2%。

为了进一步验证NLM改进算法的有效性，搭建了如图7所示的仿真模型，其参数设置见表1。

系统工作过程如下：仿真时间为3 s时，采用级联H桥多电平变流器的地面过电分相系统投入工作，并且当受电弓同时接触接触网与中性段时，进入并联运行工况；时间为4 s时，级联多电平变流器给定无功功率，给定的有功功率由0开始按106W·s-1的速率上升为电力机车的实时功率；时间为9 s时，级联多电平变流器给定的功率由电力机车的实时功率开始按106W·s-1的速率下降为0；时间为11 s时，切断地面过电分相系统。

表1　级联H桥地面过电分相系统参数

图14和图15分别为采用NLM传统算法和NLM改进算法时，新型地面过电分相系统中性段的级联H桥多电平变流器输出的有功功率和无功功率。从图14和图15可以看出：采用 NLM改进算法时系统对给定功率的跟踪更准确，动态调整时基本没有超调。

图14　2种调制算法下变流器输出的有功功率

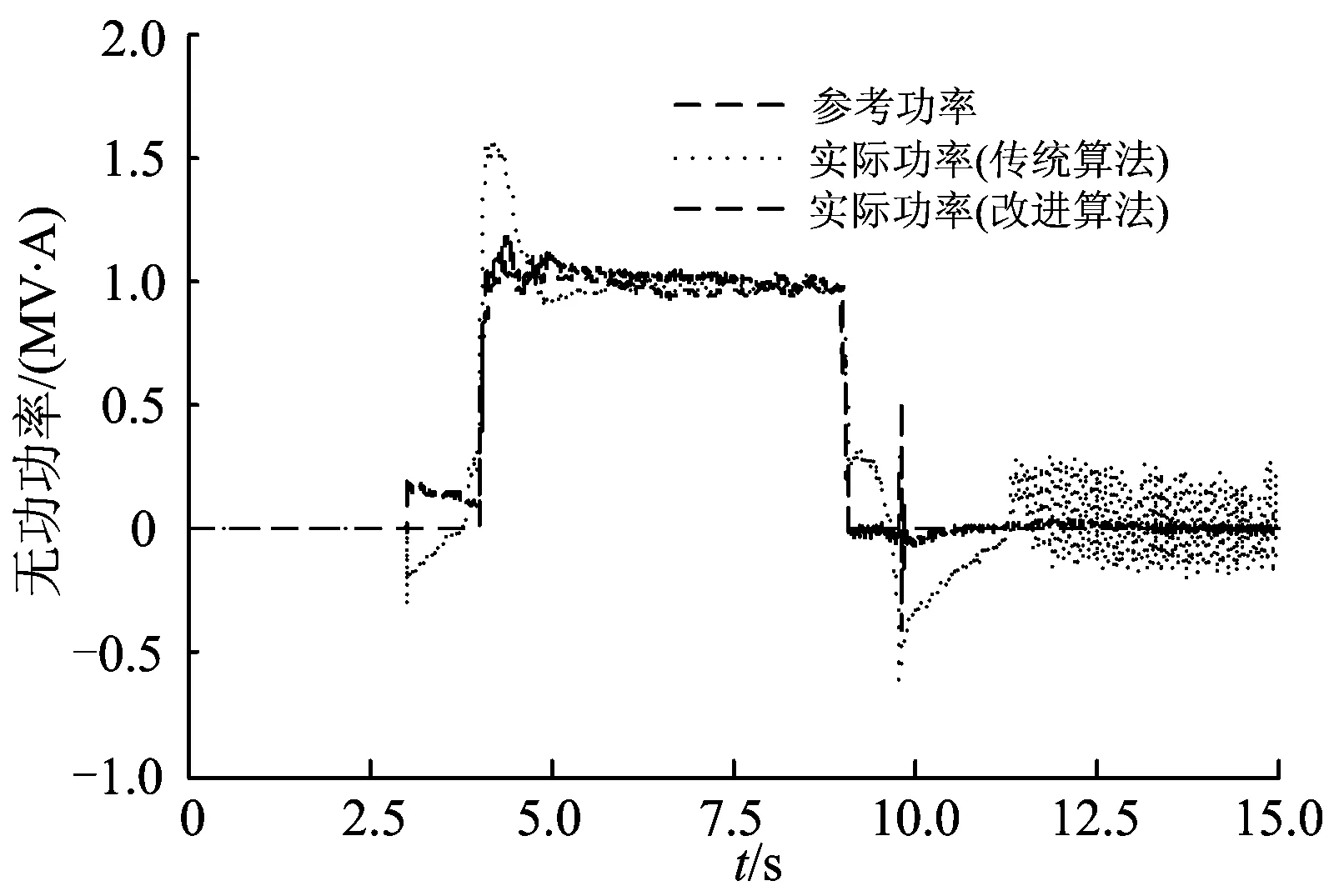
图15　2种调制算法下变流器输出的无功功率

5　结　论

(1)在级联模块数较少时，NLM传统算法最后投入工作的子模块产生的输出电压波等效面积误差最大，在6%左右；最大电压分辨率也会对地面过电分相系统的输出功率产生较大影响。

(2) NLM改进算法提高了变流器输出电压对参考电压的跟踪精度，变流器的输出功率误差平均仅约为传统算法的20.93%，而输出电压谐波含量平均仅比传统算法增大约3.2%。

(3)NLM改进算法能够提高地面过电分相系统的稳态控制精度，减小动态过程的超调。

[1]LAI J S, PENG F Z.Multilevel Converter—A New Breed of Power Converters[J].IEEE Transactions on Industry Applications，1996，32(3)：509-517.

[2]PENG F Z, LAI J S, JOHN W M.A Multilevel Voltage—Source Inverter with Separate DC Sources for Static VAR Generation[J].IEEE Transactions on Industry Applications, 1996, 32(5): 1130-1137.

[3]杨晓峰, 林智钦, 郑琼林, 等.模块组合多电平变换器的研究综述[J].中国电机工程学报，2013，33(6)：1-14.

(YANG Xiaofeng，LIN Zhiqin，ZHENG Qionglin，et al.A Review of Modular Multilevel Converters [J].Proceedings of the CSEE，2013，33(6)：1-14. in Chinese)

[4]FRANQUELO L G，RODRIGUEZ J，LEON J I，et al.The Age of Multilevel Converters Arrives[J].IEEE Industrial Electronics Magazine，2008，2(2)：28-39.

[5]RODRIGUEZ J，FRANQUELO L G，KOURO S，et al.Multilevel Converters：an Enabling Technology for High-Power Applications[J].Proceedings of the IEEE，2009，97(11)：1786-1817.

[6]ESPINOSA E， ESPINOZA J， VILLARROEL F， et al. A Novel Modulation Technique for Asymmetric Multi-Cell Inverters of 27-Level without Regeneration[C]// Annual Conference on IEEE Industrial Electronics Society (IECON2012). Montreal：IEEE, 2012: 123-128.

[7]ZHOU Y B, JIANG D Z, HU P F, et al.A Prototype of Modular Multilevel Converters[J].IEEE Transactions on Power Electronics，2014，29(7)：3267-3278.

[8]管敏渊，徐政，潘伟勇，等.最近电平逼近调制的基波谐波特性解析计算[J].高电压技术，2010，36(5)：1327-1332.

(GUAN Minyuan，XU Zheng，PAN Weiyong，et al.Analytical Calculation of Fundamental Wave and Harmonic Characteristics for Nearest Level Modulation[J].High Voltage Engineering，2010，36(5)：1327-1332.in Chinese)

[9]宋平岗，李云丰，王立娜，等.基于改进阶梯波调制的模块化多电平换流器环流抑制策略[J].电网技术，2013，37(4)：1012-1018.

(SONG Pinggang，LI Yunfeng，WANG Lina，et al.A Modified Ladder Wave Modulation-Based Circulating Current Suppressing Strategy for Modular Multilevel Converter[J].Power System Technology，2013，37(4)：1012-1018.in Chinese)

[10]熊成林，冯晓云，马俊鹏.采用级联H桥多电平变流器的地面过电分相系统[J].中国铁道科学，2016，37(1)：93-99.

(XIONG Chenglin，FENG Xiaoyun，MA Junpeng.Ground’s Passing Neutral Section System Adopting Cascade H-Bridge Multilevel Converter[J].China Railway Science，2016，37(1)：93-99.in Chinese).

[11]李永东，高跃，候轩.大容量多电平变换器PWM控制技术现状及进展[J].电力电子技术，2005，39(5)：2-6.

(LI Yongdong，GAO Yue，HOU Xuan.Development of PWM Control Technology in Multilevel Converters [J].Power Electronics，2005，39(5)：2-6. in Chinese)

[12]李强，贺之渊，汤广福，等.新型模块化多电平换流器空间矢量脉宽调制方法[J].电力系统自动化，2010，34(22)：75-79，123.

(LI Qiang， HE Zhiyuan， TANG Guangfu， et al. A Space-Vector PWM Method for a New Type of Modular Multilevel Converter[J]. Automation of Electric Power Systems， 2010， 34(22)： 75-79， 123. in Chinese)

[13]刘钟淇，宋强，刘文华.基于模块化多电平变流器的轻型直流输电系统[J].电力系统自动化，2010，34(2)：53-58.

(LIU Zhongqi，SONG Qiang，LIU Wenhua.VSC-HVDC System Based on Modular Multilevel Converters[J].Automation of Electric Power Systems，2010，34(2)：53-58. in Chinese)