基于回归模型的方法分析半干旱流域的降雨径流关系

余　超，晁丽君，张梦婕，朱家昌，孙靖智

(1.河海大学 理学院， 南京　210098； 2.河海大学 文天学院， 安徽 马鞍山　243031；

3.河海大学 水文水资源学院， 南京　210098； 4.天津市水务局,天津　300074；

5.辽宁省水利厅， 沈阳　110003)



基于回归模型的方法分析半干旱流域的降雨径流关系

余超1，晁丽君2，张梦婕3，朱家昌4，孙靖智5

(1.河海大学 理学院， 南京210098； 2.河海大学 文天学院， 安徽 马鞍山243031；

3.河海大学 水文水资源学院， 南京210098； 4.天津市水务局,天津300074；

5.辽宁省水利厅， 沈阳110003)

摘要：以半干旱流域大阁流域为例，通过回归模型改进半干旱流域降雨径流关系，用3种方法建立回归方程，然后对3种方法的结果进行评定。比较3种方法的合格率、许可误差和确定性系数。结果表明：采用方法3在大阁流域模拟降雨径流达到了预报精度，很好地描述了降雨径流关系，从而为改进半干旱流域的降雨径流关系提供新思路。

关键词：回归模型； 降雨径流；相关性；半干旱流域；评定方法；多因子；可分离变量

基于回归模型方法[1]分析降雨径流关系[2]是将数据集在空间或时间上外推到其他情形的基本统计计算机技术。数据用于以因变量和一个或多个自变量或解释变量的收集整理，统计计算用于推导建立一个因变量与自变量的相关关系的方程。

一次降雨的产流量和很多因素有关，也就是R=f(P,Pa,i,季节，…)[3]的函数关系。本方法以流域产流的物理机理为基础，以主要影响因素为参变量，建立各因素与产流量R之间的关系。这里的各因素包括降雨量P、前期雨量指数Pa、降雨强度i、季节等等。

1回归方程的描述

多元线性回归模型[4]是描述因变量y依n项自变量x1,x2,x3,…,xn和误差项ε取值的方程。

1.1线性回归模型

设线性回归模型的一般形式为

(1)

若有m组由因变量y和n项自变量x1,x2,x3,…,xn数据构成的样本，依式(1)可组成线性回归模型，可用矩阵表示为

(2)

其中：

利用最小二乘法原理[5]求方程组(2)，从而建立线性回归方程。

1.2非线性回归模型

当拟合曲线是非线性时，往往按下述方法求其回归方程：

假设有n个影响因子：

(3)

首先假设y是关于各因子的可分离变量函数[6]，即

(4)

在自变量x1,x2,x3,…,xn中找出对倚变量y影响最大的主要因子。假设x1对y影响最大，建立数学模型：

(5)

以此确定主要因素与y的函数关系。当取p=2时，即为最小二乘法。

确定y1=f1(x1)及残差Δy1=y-y1。由于y是x1,x2,x3,…,xn的函数，自y中分离x1的函数y1=f1(x1)后，残差Δy1应近似为x2,x3,…,xn的函数。再分析Δy1与x2,x3,…,xn的相关关系。比较各因素与残差的相关性，往往会应用3种方法。

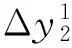
(6)

方法2利用所建立的数学模型(5)分别求出Δy1与x2,x3,…,xn的函数，即Δy1=f(x2),Δy1=f(x3),…,Δy1=f(xn)，然后建立超定方程：

(7)

用最小二乘法求出a2,a3,…,an，由此得出

(8)

方法3利用所建立的数学模型(5)求出Δy1与x2,x3,…,xn的函数：

(9)

2相关分析

在研究两个水文序列之间的关系时，可采用相关分析法[7]。例如对于一次洪水的径流深和流域一次洪水的降雨量，可以通过互相关来表示同一次洪水的径流量与降雨量之间的关系。

水文序列Xt和Yt的相关系数ρk(X,Y)定义为

(10)

式中C(X,Y)为序列Xt和Yt的互协方差。通常应用式(11)由样本序列(Xt,Yt;t=1,2,…,n)估计互相关系数。

(11)

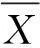
3降雨径流关系中各要素的计算原理

3.1流域平均次降雨量计算

流域平均次降雨量又称面雨量，是指一次降雨过程中整个流域面上的平均累计降雨量。推求流域平均次降雨量最常用的方法有算术平均法和垂直平分法(又叫做泰森多边形法)，也有用绘制等雨量线图来推求的。

(12)

其中：ωi为流域内各雨量站权重(无量纲)；Pi为流域内各雨量站的时段降雨量(mm)；P为时段流域平均降雨量(mm)；n为流域内雨量站的个数(无量纲)。

3.2前期影响雨量的计算

前期影响雨量Pa为衡量流域湿润程度的指标[8]，反映流域蓄水量的大小。Pa越小表示流域的干旱程度越大；Pa越大表示流域的湿润程度越大。流域前期影响雨量(Pa值)采用递推公式计算，并以流域土壤最大损失量(Im值)进行控制。Im为流域最大损失量，范围一般在80～120 mm。本次研究中Im统一取为120 mm。单站前期影响雨量Pa的计算式为[9]

(13)

其中：Pa,t，Pa,t+1分别为第t天和第t+1天开始时刻的前期影响雨量(mm)，Pa,t+1≤Im；Pt为第t天该站的日降雨量(mm)；Ka为流域土壤含水量消退系数(无量纲)，取值范围一般为0.8～0.95。

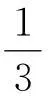
3.3雨强的计算

根据前面计算的流域平均次雨量P可以推出雨强i：

(14)

其中：P为时段流域平均降雨量；t为本次洪水的历时；i为雨强。

3.4地表径流量的计算

产流是流域内各种径流成分的生成过程，也就是流域下垫面对降雨的再分配过程。当降雨强度小于下渗强度时，降落在地面的雨水将全部渗入土壤；当降雨强度大于下渗能力时，雨水除按下渗能力入渗外，超出下渗能力的部分便形成地面径流。渗入土壤中的水量除被土壤蒸发和植物吸收散发而损耗掉外，余下的补充了土壤含水量。当土壤包气带的水量超过田间持水量时，则产生壤中径流，同时通过浅层地下径流和深层地下径流补给河流。因此，一次降水的产流过程是由不同水源组成的径流过程。

3.4.1流量过程的分割

由于地面径流和地下径流有不同的汇流特性[10]，根据实测洪水流量过程线，采用斜线分割法对地面径流和地下径流进行划分。首先，从整个流量过程线中分割出前、后期径流和深层基流，并获得本次降雨所形成的流量过程，然后进行地表、地下流量过程的分割，这就是所谓的基流分割[11]。该方法的基本思路：先寻找洪水过程的直接径流终止点，然后用斜线连接涨点与终止点，则斜线上部为地面径流，下部为地下径流。

对于半干旱、干旱地区，地面径流终止点可用目估法确定。对于湿润、半湿润地区，地面径流终止点可通过经验法确定。该方法是通过对实测资料的分析确定洪峰时间到地面径流终止点的时距N[12]，并认为同一流域的N值是常数。求取N的经验公式为

(15)

其中：F为流域面积(km2)；N为洪峰时间到地面径流终止点的时距(h)。

3.4.2地表径流量的计算

在分割出一次降雨所形成的地面径流过程线后，即可根据起涨点、终止点及洪水过程线包围的面积计算次洪径流深。计算公式为

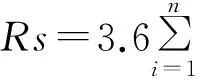
(16)

其中：Rs为流域地面径流深(mm)；Qi为流域时段流量(m3/s)；Δti为计算时段(h)，常取1 h；F为流域面积(km2)；3.6为单位换算系数(无量纲)。

4精度评定

径流深预报以实测值的20%作为许可误差，当一次预报的误差小于许可误差时为合格预报。

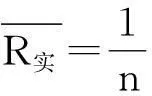
5流域概况

大阁流域位于密云水库流域。密云水库建于1960年，蓄水以来，为京、津、冀部分地区工农业与城市生活用水发挥了巨大作用。潮白河密云水库以上流域位于东经115°30′～117°30′，北纬 40°20′～41°30′。东部和东北部与滦河流域为界，北面与内陆河闪电河为邻，西与永定河支流洋河流域相邻。密云水库流域面积15 788km2，占潮白河流域面积18 000km2的88%。本流域除水库库区附近地势稍低，其高程一般在海拔500m以下外，其他地方地势均较高，具有山高、坡陡、沟深、流急的特点，河道比降较大。东支潮河发源于河北省承德地区，河源至水库全长220km，河道平均比降为1.87%。西支白河发源于河北省张家口地区，河源至水库全长248km，河道平均比降为4.87%。流域内基本属于土石山区，一般土层较薄，植被较好，但流域内各地差异较大，不少地方岩石裸露，裂隙较大。

密云水库流域面积较大，本次研究采用潮河的大阁流域。大阁位于东经116°41′，北纬41°11′，流域面积为1 850km2。该流域属于中纬度大陆性季风气候，据1951—1981年资料统计，流域平均降雨量为525mm，暴雨分布以库区为中心，分别沿潮白河向东北和西北方向渐减。潮河上游多年平均降雨量约为500mm。降雨量主要集中在6～9 月份，尤其集中在7～8月份。

6算例

选取大阁流域为例，倚变量为流域地面径流深Rs，自变量分别是流域平均次降雨量P、前期影响雨量Pa、雨强i，共44组资料。本次算例采用泰森多边形法计算流域平均次降雨量P[13-18]。大阁流域雨量站及权重和位置如表1所示。

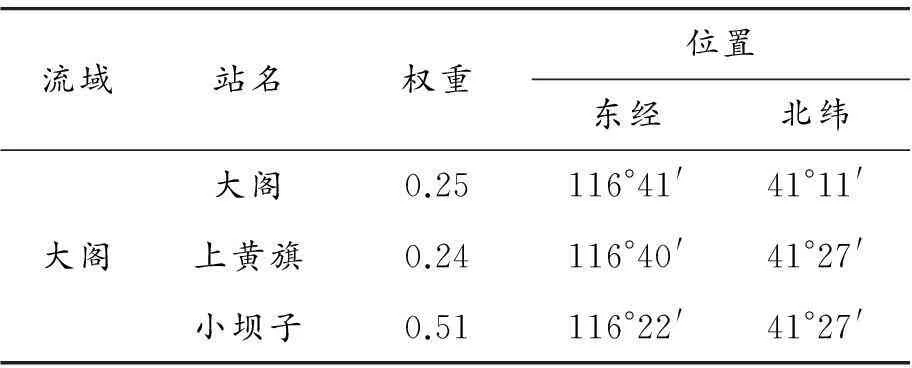
表1　大阁流域雨量站及其权重、位置

6.1计算相关性

采用式(10)计算出倚变量流域地面径流深Rs与自变量流域平均次降雨量P、前期影响雨量Pa、雨强i各自的相关系数，结果如表2所示。

表2　相关系数

通过比较可以看出：倚变量流域地面径流深Rs与流域平均次降雨量P相关系数最大，其次是雨强i，最小的是前期影响雨量Pa。这里采用的是Pearson 相关性和显著性双侧检验。

6.2计算结果

本算例分别采用方法1～3进行计算。选取大阁流域44场洪水中的前30场洪水用于模型的参数率定，后14场用于预报模型验证。由相关系数可知：倚变量流域地面径流深Rs与流域平均次降雨量P的相关系数最大。利用式(5)拟定Rs=f(P)，计算结果如表3所示，式(5)中取p=2时即为最小二乘法。

表3　Rs= f(P)计算结果

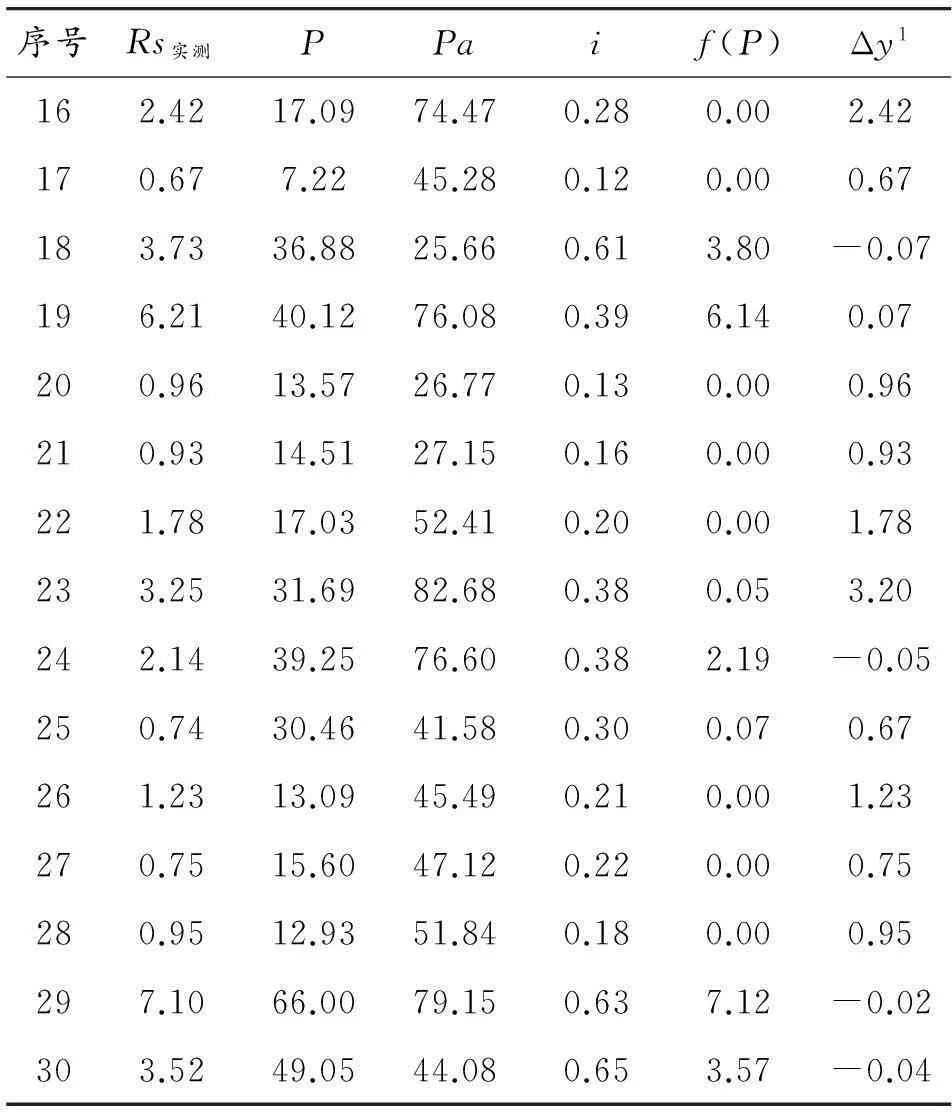
序号Rs实测PPaif(P)Δy1162.4217.0974.470.280.002.42170.677.2245.280.120.000.67183.7336.8825.660.613.80-0.07196.2140.1276.080.396.140.07200.9613.5726.770.130.000.96210.9314.5127.150.160.000.93221.7817.0352.410.200.001.78233.2531.6982.680.380.053.20242.1439.2576.600.382.19-0.05250.7430.4641.580.300.070.67261.2313.0945.490.210.001.23270.7515.6047.120.220.000.75280.9512.9351.840.180.000.95297.1066.0079.150.637.12-0.02303.5249.0544.080.653.57-0.04

采用方法1计算出Δy1后用式(5)拟定Δy1=f(i)，而后计算Δy2，即Δy2=f(P)+f(i)-Rs实测。用式(5)拟定Δy2=f(Pa)，最后得到Rs预报值=f(P)+f(i)+f(Pa)，计算结果如表4所示。

表4　 方法1计算结果

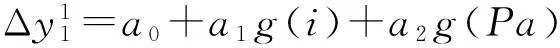
采用方法3计算出Δy1后用式(5)拟定Δy1=g(i,Pa)，得到Rs预报值=f(P)+g(i,Pa)，方法2、3的计算结果如表5所示。

表5　方法2、3计算结果

6.3误差评定

根据径流深预报以实测值的20%作为许可误差,且许可误差小于20 mm时点据评定为合格。对大阁流域的14场洪水进行方案评定，结果如下：方法1得到的合格率QR为71.4%，相对平均误差为18.9%，确定性系数DC为0.997；方法2得到的合格率QR为42.9%，相对平均误差为26%，确定性系数DC为0.995；方法3得到的合格率QR为78.6%，相对平均误差为18.3%，确定性系数DC为0.995。误差计算结果如表6所示。

从评定结果可以看出：3种方法的确定性系数都很高，达到评定要求，但是只有方法3合格率达到乙级精度要求。分析数据可以看出：产生这种现象的原因是大阁流域的径流深相对较小，但是其中会出现一些大数，这就导致确定性系数普遍很高。

根据误差评定出的结果，大阁流域应选取方法3进行径流深的预报。通过与文献[9]中应用的降雨径流相关图法进行比较，运用降雨径流相关图法的合格率QR只有34%，相对平均误差为36%；运用回归模型的合格率QR为78.6%，相对平均误差为18.3%，大大提高了精度。

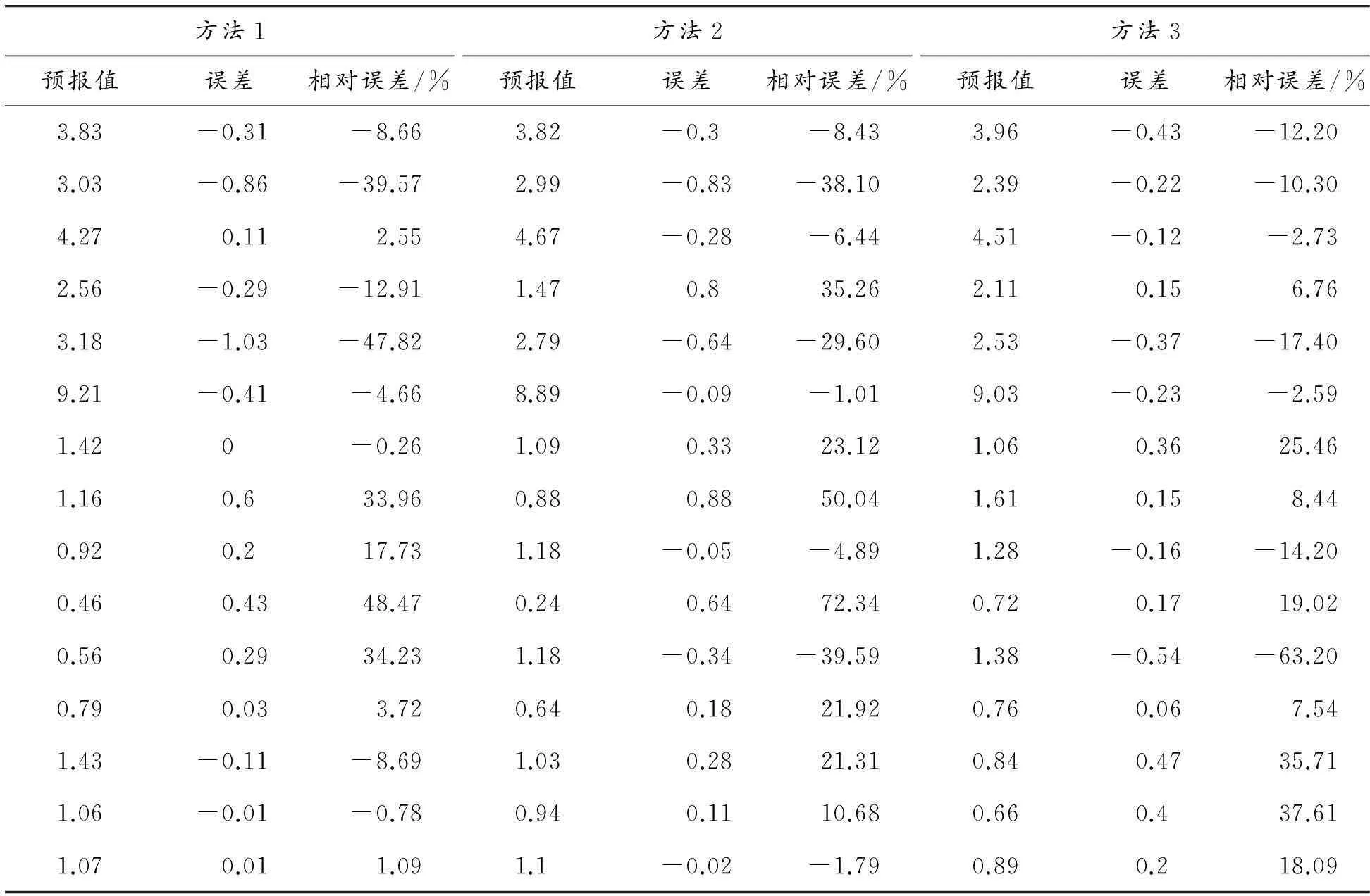
表6　误差计算结果

7结论

1) 基于回归模型的分析方法可用于估算模型参数或无观察资料地区的径流深。

2) 通过与文献[9]在大阁流域的比较可以看出：预报精度得到明显提高，说明基于回归模型的分析方法可以弥补降雨径流相关图在半干旱地区应用的不足。

3) 模拟的关键点是在最终确定方程时如何选取自变量。

4) 回归的预报值取决于模型与原始数据的拟合情况。

5) 所有预报成果都应当计算误差联系起来，这种估算标准误差可表述预报结果的不确定性。

6) 预报成果所依据数据的代表性好，其估算的标准误差就小；代表性差，标准误差就大。

参考文献：

[1]袁慰平.计算方法与实习[M].南京:东南大学出版社,1991.

[2]贝文.降雨—径流模拟[M].马俊，译.北京:中国水利出版社,2006.

[3]芮孝芳.产流模式的发现与发展[J].水利水电科技进展,2013,33(1):2-5.

[4]张润楚.多元统计分析[M].北京:科学出版社,2006.

[5]李庆扬.科学计算方法基础[M].北京:清华大学出版社,2006.

[6]任英.变量可分离函数的重要性质和应用[J].大连轻工学院学报,1992,12(30)：66-71.

[7]丁晶,高荣松,邓育仁.随机水文学[J].四川水力发电,1985(2)：128-129.

[8]芮孝芳.流域水文模型研究中的若干问题[J].水科学进展,1997,8(1):94-98.

[9]李致家，于莎莎，李巧玲，等.降雨-径流关系的区域规律[J].河海大学学报(自然科学版)， 2012,40(6):598-603.

[10]包为民.水文预报[M].北京:中国水利水电出版社，2009:25-28,328-329.

[11]倪雅茜,张文华,郭生练.流量过程线分割方法的分析探讨[J].水文,2005,25(3):10-14.

[12]RAY K,LINSLEY J,MAX A,et al.Hydrology for Engineers[M].3rd ed.New York:McGraw-Hill,Inc，1982：120-140.

[13]龙胤慧,廖梓龙.基于泰森多边形法的庆阳市面雨量计算[J].河北工程大学学报(自然科学版),2012(3):64-67.

[14]张德伟,崔永生.在计算机上应用泰森多边形法计算流域平均面雨量[J].水文,1991(1):52-53.

[15]王玉德.基于ArcGIS的泰森多边形法计算区域平均雨量[J].吉林水利,2014(6):58-60.

[16]赵良民.泰森多边形法计算机程序的研制[J].水利科技,2005(1):55-56.

[17]鲁南,菅瑞卿,刘洪波.流域变雨量站泰森多边形法的微机处理原理[J].黄河水利职业技术学院学报,2001(1):1-2.

[18]杨玮,韦宏鹄.利用泰森多边形法分析汾河流域中段降水量[J].山西水利,2006(2):72-73.

(责任编辑刘舸)

Methods Analysis on Rainfall-Runoff of Semi-Arid Basin Relationship Based on Regression Model

YU Chao1, CHAO Li-jun2, ZHANG Meng-jie3, ZHU Jia-chang4,SUN Jing-zhi5

(1.College of Science, Hohai University, Nanjing 210098,China;2.Wentian College, Hohai University, Maanshan 243031, China;3.College of Hydrology and Water Resources, Hohai University, Nanjing 210098, China;4.Tianjin Water Authority Water Conservancy Department, Tianjin 300074,China;5. Liaoning Provincial Department of Water Resources, Shenyang 110003,China)

Abstract:The relationship between rainfall and runoff of the semi-arid region was revised by using the regression model. Taking the Dage basin that is a semi-arid basin for example, three methods were used to build the regression equation. The percent of pass, the permissible error and the deterministic coefficient of the three methods were calculated and compared to evaluate the performance of them. The results indicate that the third method shows the best precision in Dage basin and has a good description of the relationship between rainfall and runoff in semiarid region. It is an effective approach to revise the relationship between rainfall and runoff in semiarid region.

Key words:regression model; rainfall-runoff; correlation; semi-arid basin; evaluation method; multi-factor; separable variable

文章编号：1674-8425(2016)02-0058-08

中图分类号：P338

文献标识码：A

doi:10.3969/j.issn.1674-8425(z).2016.02.011

作者简介：余超(1989—)，男，江西人，硕士研究生，主要从事水文预报和流域水文模型研究；通讯作者 晁丽君(1987—)，女，陕西人，主要从事水文预报和流域水文模型研究。

基金项目：国家自然科学基金资助项目(41130639，51179045, 41101017，41201028)；院级科研项目(WT14001ZD)

收稿日期：2015-03-27

引用格式：余超，晁丽君，张梦婕，等.基于回归模型的方法分析半干旱流域的降雨径流关系[J].重庆理工大学学报(自然科学版)，2016(2):58-65.

Citation format：YU Chao, CHAO Li-jun, ZHANG Meng-jie,et al.Methods Analysis on Rainfall-Runoff of Semi-Arid Basin Relationship Based on Regression Model[J].Journal of Chongqing University of Technology(Natural Science)，2016(2):58-65.