基于遗传算法优化的车辆主动悬架模糊PID控制
赵 强,何 法,王 鑫,刘杰雄
(1.东北林业大学 交通学院,哈尔滨 150040;
2.华晨汽车工程研究院,沈阳 110141)
基于遗传算法优化的车辆主动悬架模糊PID控制
赵强1,何法1,王鑫1,刘杰雄2
(1.东北林业大学 交通学院,哈尔滨150040;
2.华晨汽车工程研究院,沈阳110141)
摘要:针对汽车主动悬架模糊PID控制器参数的最优选取问题,利用遗传算法的全局优化能力和并行能力优化模糊PID控制器的量化因子及其PID参数的修正系数。以汽车行驶平顺性和接地性等作为综合评价指标,建立包含车身垂直加速度、悬架动行程和轮胎动载荷3项指标的目标函数,采用遗传算法进行控制器参数优化,以Granada车参数为例进行控制仿真。仿真结果表明:主动悬架采用基于遗传算法优化的模糊PID控制后,其性能优于无优化的模糊PID控制以及相应的被动悬架。
关键词:主动悬架;模糊PID控制;遗传算法
悬架是车辆的重要总成之一,能够传递车轮和车身之间的一切力和力矩,衰减由路面不平度产生的振动冲击[1]。常规的被动悬架内部没有能量供给装置,悬架刚度和阻尼只能适应一定的载荷、车速以及某些路面情况,因此在不同路面和载荷条件下车辆的平顺性等指标都不如参数可调悬架。
主动悬架装有主动作动器,能够根据输入参数产生最优的控制力,使悬架具有良好的减振性能,从而提高车辆的平顺性和接地性[2]。选择合理的控制算法能够较好地发挥主动悬架的性能。模糊PID控制综合了模糊控制和PID控制的特点,具有结构简单、鲁棒性强等优点[3]。但是,模糊PID控制器的参数选取一般采用试凑等方法,有一定局限性,很难达到最优状态。本文利用遗传算法的全局优化能力和并行能力,对模糊PID控制器的量化因子和修正系数进行优化,搜索以上参数的最优值,完成控制器设计,并应用到Granada 车型;通过控制仿真,与无参数优化的模糊PID主动悬架以及被动悬架进行比较分析,验证控制优化的有效性。
1模型建立
1.1主动悬架动力学方程的建立
为了研究的方便,本文选取简化的2自由度 1/4 车模型作为研究对象,如图1所示。
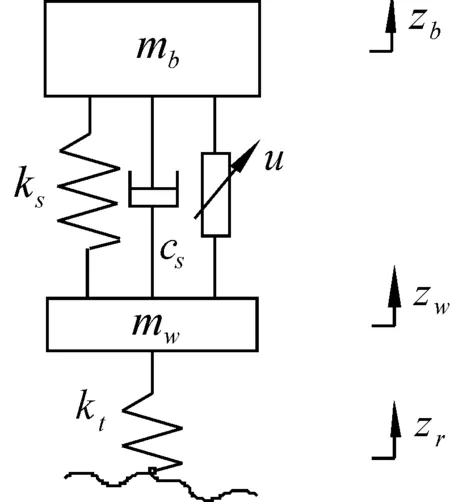
图1 1/4车体主动悬架简化模型
参照图1模型,根据牛顿第二定律建立主动悬架的运动微分方程:
(1)
(2)
式中:mb是簧载质量;mw是非簧载质量;kt是轮胎刚度;cs是阻尼器的阻尼系数;ks是悬架弹簧刚度;u是主动控制力;zb是簧载质量垂向位移;zw是非簧载质量垂向位移;zr是路面输入激励。
1.2路面输入模型
连续的随机路面通常用白噪声速度谱和相应的时域形式描述[4]。本文采用由Thompson提出的白噪声经积分器产生随机路面的方式建立路面输入模型。
时间频域内路面位移功率谱密度和速度功率谱密度函数表达式为:
(3)
(4)
式中:f为时间频率(Hz);v为汽车速度(m/s);n0=0.1为参考空间频率(m-1);Gq(n0)为路面不平度系数(m3)。
当汽车速度v一定时,速度功率谱密度为常数,路面轮廓可由白噪声经过积分器产生:
(5)
式中:k0=2πn0(Gq(n0)u)1/2;w(t)为白噪声强度;x(t)为路面输入模型函数。
本文选择C级路面下的不平度来建模,车速选择40 km/h,经计算白噪声强度为256×10-6dB,积分器后面的增益系数为1.3×10-5π。路面幅度变化时域如图2所示。
1.3仿真参数选取
本文选择福特Granada轿车后悬架单轮模型为研究对象,悬架机械参数见表1。
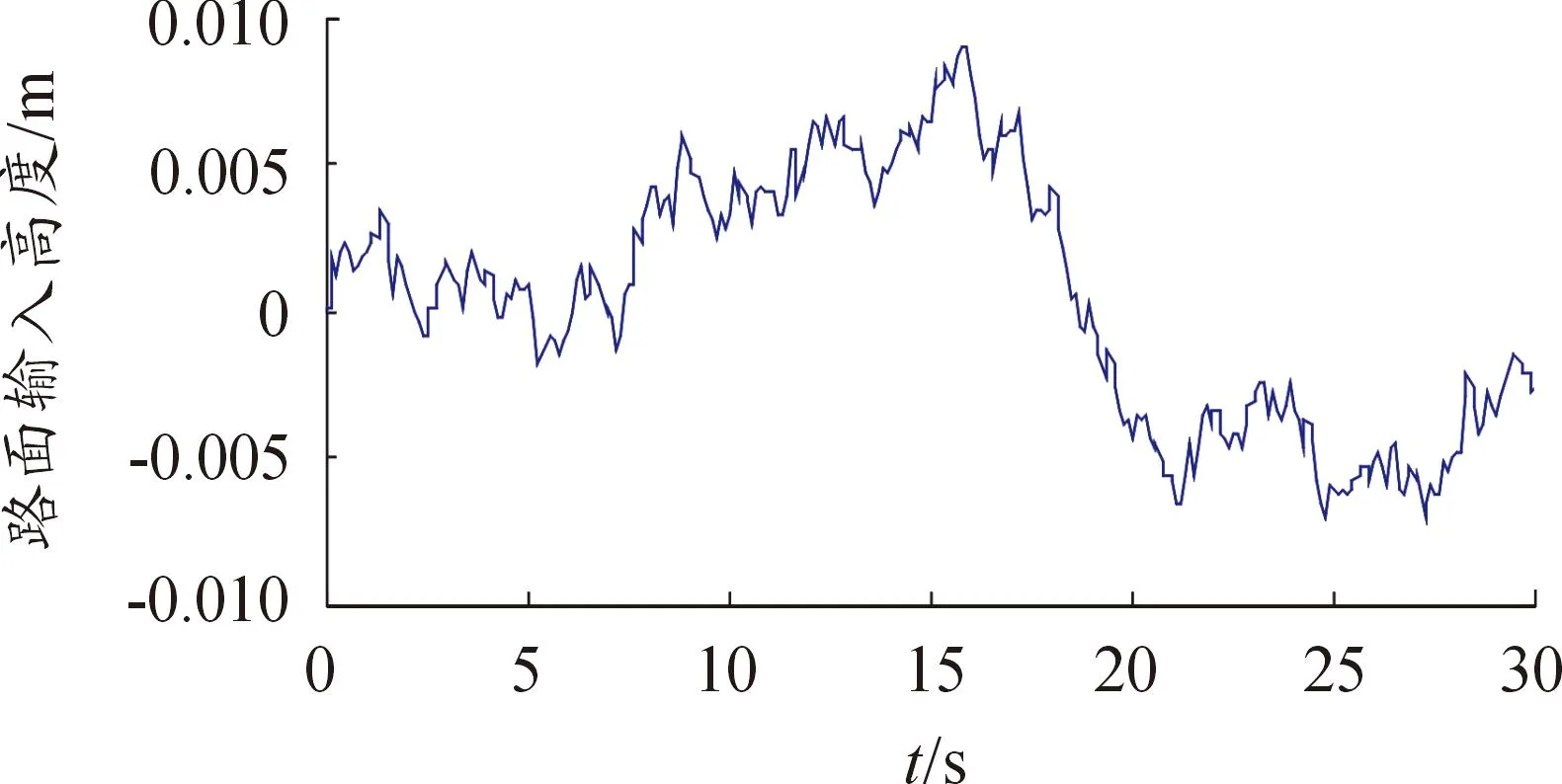
图2 C级路面幅度变化时域

簧载质量mb/kg非簧载质量mw/kg悬架刚度ks/(N·m-1)轮胎刚度kt/(N·m-1)阻尼系数cs/(N·s·m-1)317.545.4220001920001500
2遗传算法优化的模糊PID控制器的设计
2.1主动悬架模糊PID控制
以PID控制方法为基础,运用模糊算法思想,把被控量的偏差e和偏差变化率ec作为模糊推理的输入变量,通过模糊算法规则整定PID的控制参数,构成了二维的模糊PID控制器[5]。此方法将模糊控制的良好动态跟踪能力和PID控制的良好稳定性能结合起来,其原理见图3。
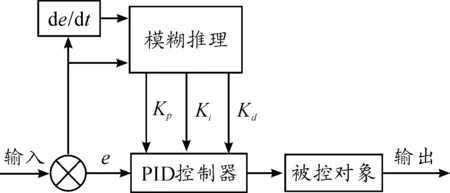
图3 模糊PID控制原理
将偏差e和偏差变化率ec作为控制器的输入,可以得到修正后的PID参数值:
(6)
(7)
(8)
式中:Kzp,Kzi,Kzd为PID最终参数设定值;Kp0,Ki0,Kd0为PID初始参数设定值;qkp,qki,qkd为修正系数;Kp,Ki,Kd为模糊修正值。
控制器输入变量e,ec和输出模糊变量Kp,Ki,Kd的模糊论域都选为[-3,3],并定义它们的模糊子集为[NB,NM,NS,ZO,PS,PM,PB]。量化因子Ke=25,Kec=17;比例因子Ku=8,Kp0=168,Ki0= 2,Kd0=0.1,qki=56,qki=6.7,qki=0.03。隶属函数均选取三角形函数,模糊推理方法选择Mamdani min-max法,模糊判决选择重心法。根据专家知识和操作者的经验[6],总结出的模糊控制规则分别对应表2~4。
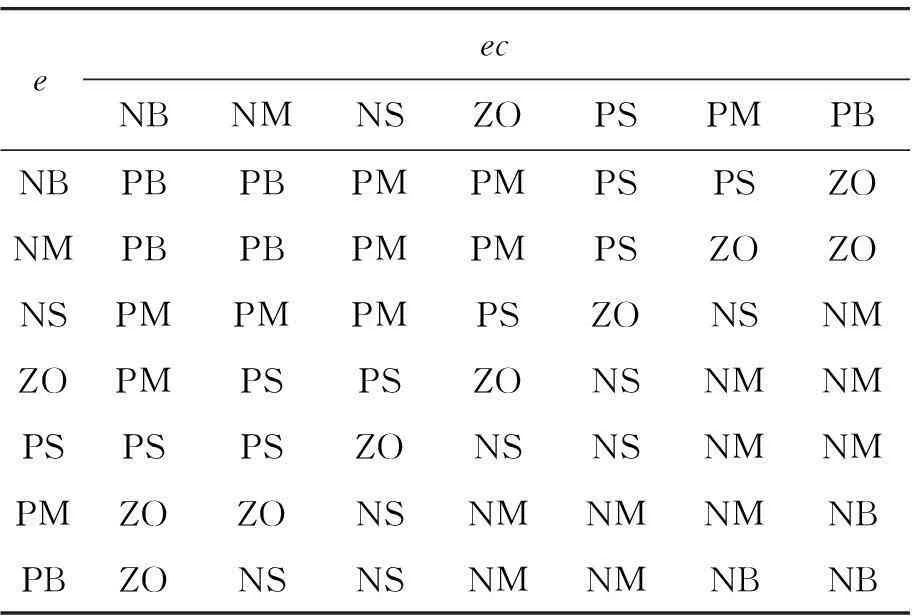
表2 Kp的模糊控制规则
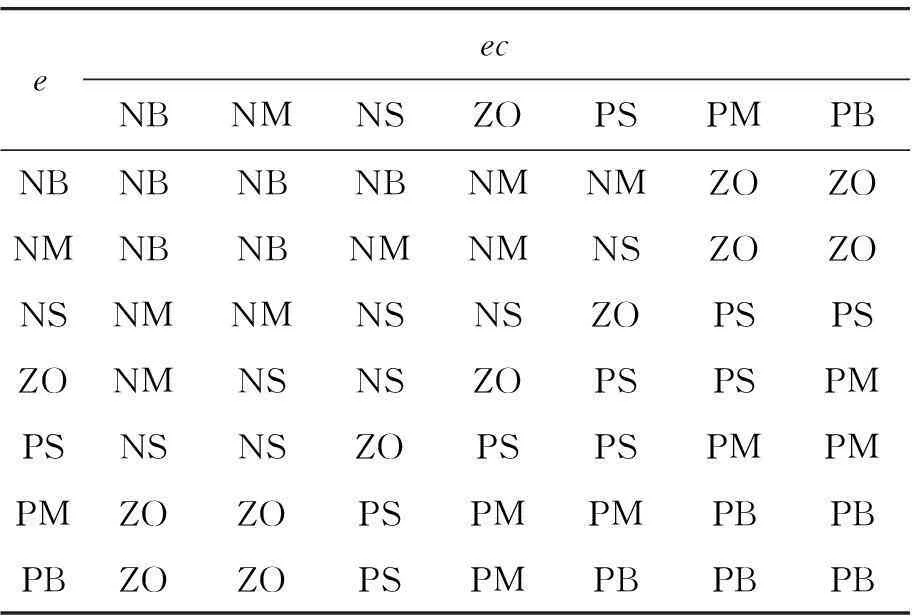
表3 Ki的模糊控制规则
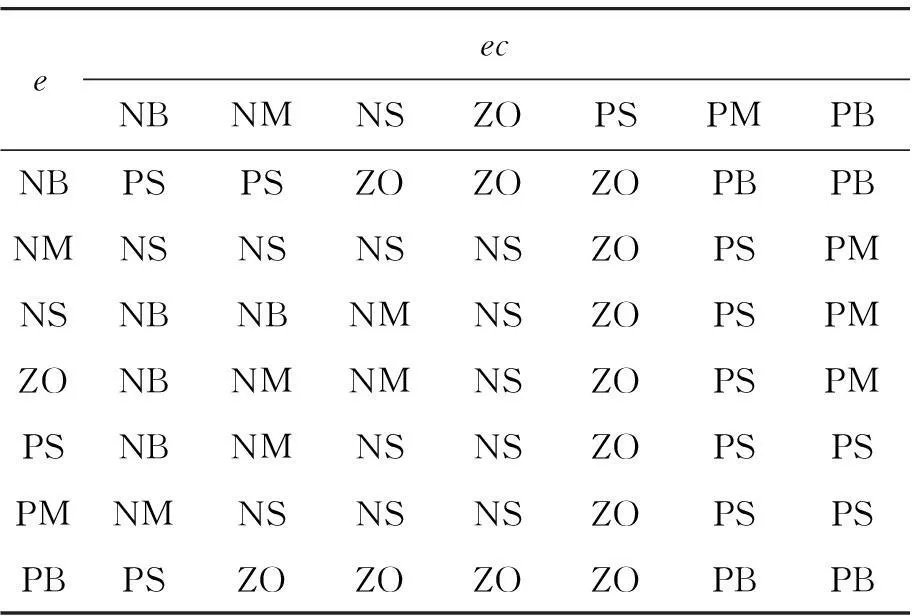
表4 Kd的模糊控制规则
2.2基于GA的模糊PID控制器参数优化
2.2.1控制器优化模型
本文选取量化因子和PID控制器3个修正系数作为设计变量,每个设计变量的上、下限值见表5。
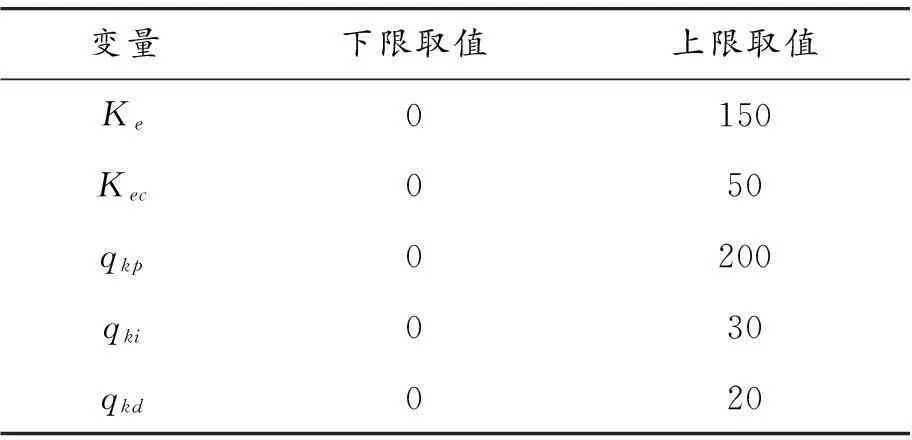
表5 设计变量的上、下限值
2.2.2目标函数选取
汽车悬架设计中平顺性的主要性能指标:代表乘坐舒适性的车体质心垂直振动加速度(ACC);影响车身姿态且与结构设计和布置有关的悬架动行程(SWS);代表轮胎接地性的轮胎动态力(DTL)[7]。由于这3个性能指标的单位和数量级都不一样,因此将其除以相对应的被动悬架性能指标即可得到优化的目标函数:
(9)
式中:Q(x)为目标函数;J1为主动悬架车体垂直加速度的均方根值;J2为主动悬架的悬架动行程的均方根值;J3为主动悬架轮胎动态力的均方根值;ACCpas为被动悬架车体质心垂直振动加速度的均方根值;SWSpas为被动悬架的悬架动挠度的均方根值;DTLpas为被动悬架轮胎动态力的均方根值。
2.2.3控制器的GA优化算法
遗传算法是人工智能领域中解决最优化问题的一种高效的随机搜索算法,其通过选择运算、交叉运算、变异运算等操作,寻求一个对于种群有最大适应度的最优解。
1) 染色体编码
将优化模型中的5个变量从左到右依次连接成编码串x=(Ke,Kec,qkp,qki,qkd),这样的编码串就代表种群中1个个体。每一个个体都是可行解,并根据表5产生初始种群。种群规模为100,并在迭代的过程中保持不变。
2) 适应度函数选择
遗传算法中的适应度函数要满足最大化的要求,而目标函数是求取最小值的问题,因此选取目标函数的倒数作为本次遗传算法优化的适应度函数,如式(10)所示。适应度值越大,说明控制效果越优良。
(10)
式中:Kemin,Kecmin,qkpmin,qkimin,qkdmin为设计变量的下限值;Kemax,Kecmax,qkpmax,qkimax,qkdmax为设计变量的上限值。
3) 选择、交叉和变异操作
若选择操作以较大的概率作用于种群,则适应度高的个体作为父代遗传到下一代的概率就高。本文选择概率设定为0.9。
交叉操作是按照较大的概率作用于个体,把两个父代个体的部分结构加以替换重组,进而产生新个体[8]。本文的交叉概率设定为0.8。
变异操作是以较小的概率改变个体的某些部位,生成新个体。本文的变异概率设定为0.02。
4) 终止条件
遗传算法不仅可以用最大迭代次数来限制程序运行,还可以用适应度函数来判断终止条件[9]。本文用最大迭代次数作为优化的一个终止条件。当运行到指定的迭代次数时,遗传算法程序会自动停止,并输出最优解。本文最大迭代次数选择20。
在优化过程中调用遗传算法运行程序,整个优化程序的流程见图4。
本文在采用遗传算法优化控制器参数时将调用图5模型。模型输出悬架平顺性性能指标的均方根值,并传递给GA的优化主程序。进行20次迭代后,得到适应度值变化曲线,见图6。优化控制代码见图7。
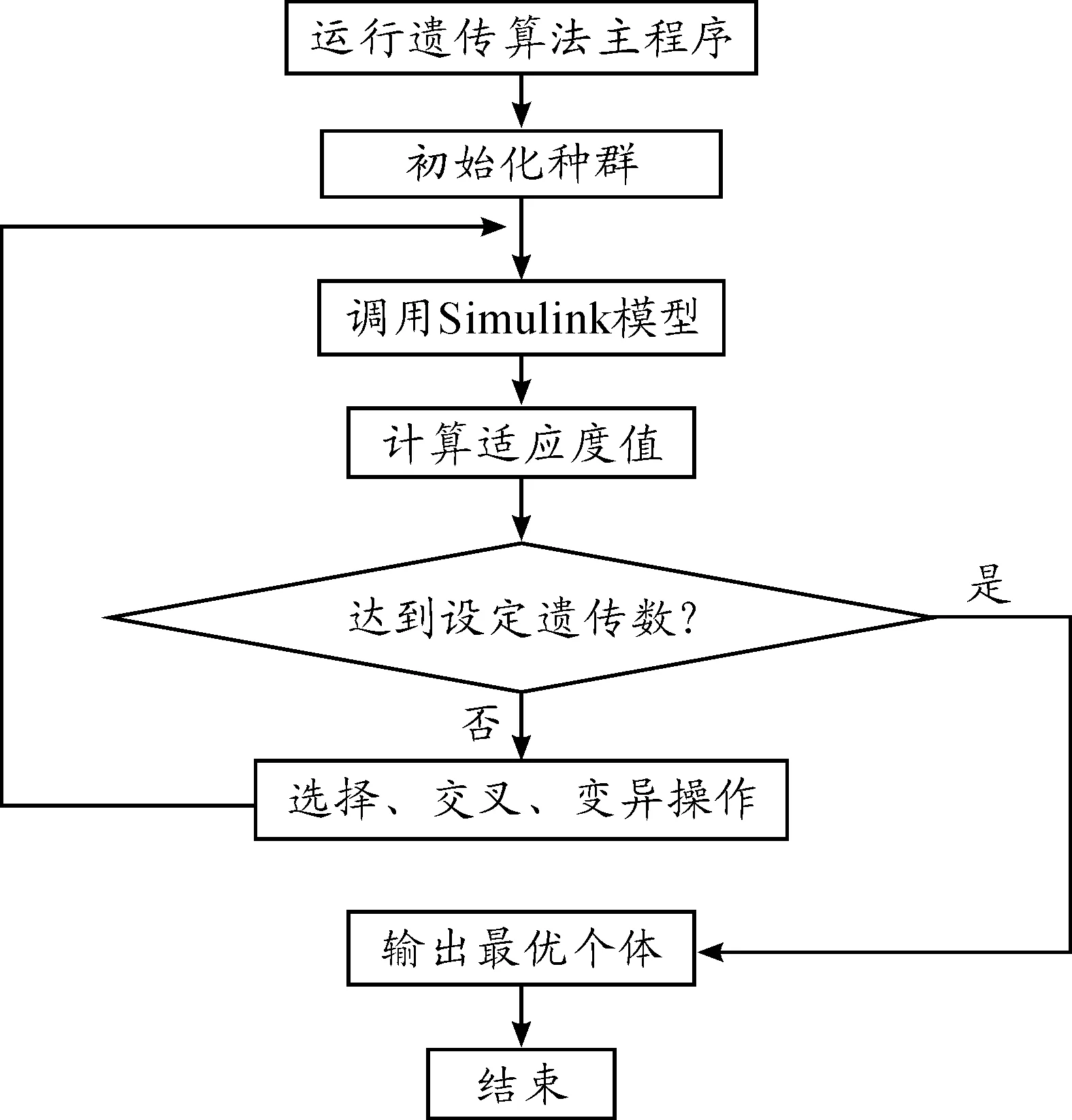
图4 遗传优化流程
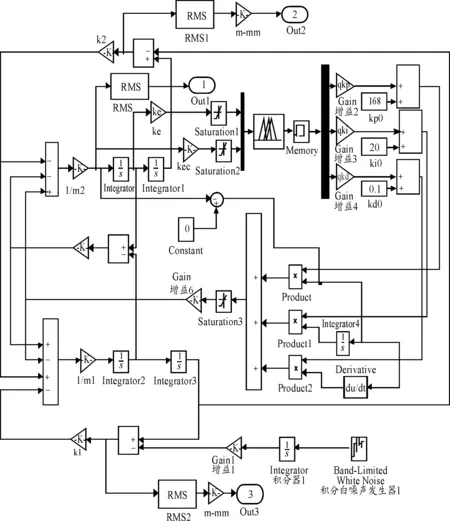
图5 遗传算法调用模型
由图6可以看出:最优个体的适应度函数值不断增加,最终至0.476 2,此时对应的最优个体为(Ke,Kec,qkp,qki,qkd)=(91.505 1,30.243 3,168.268 3,17.597 1,9.469 3),见图1。
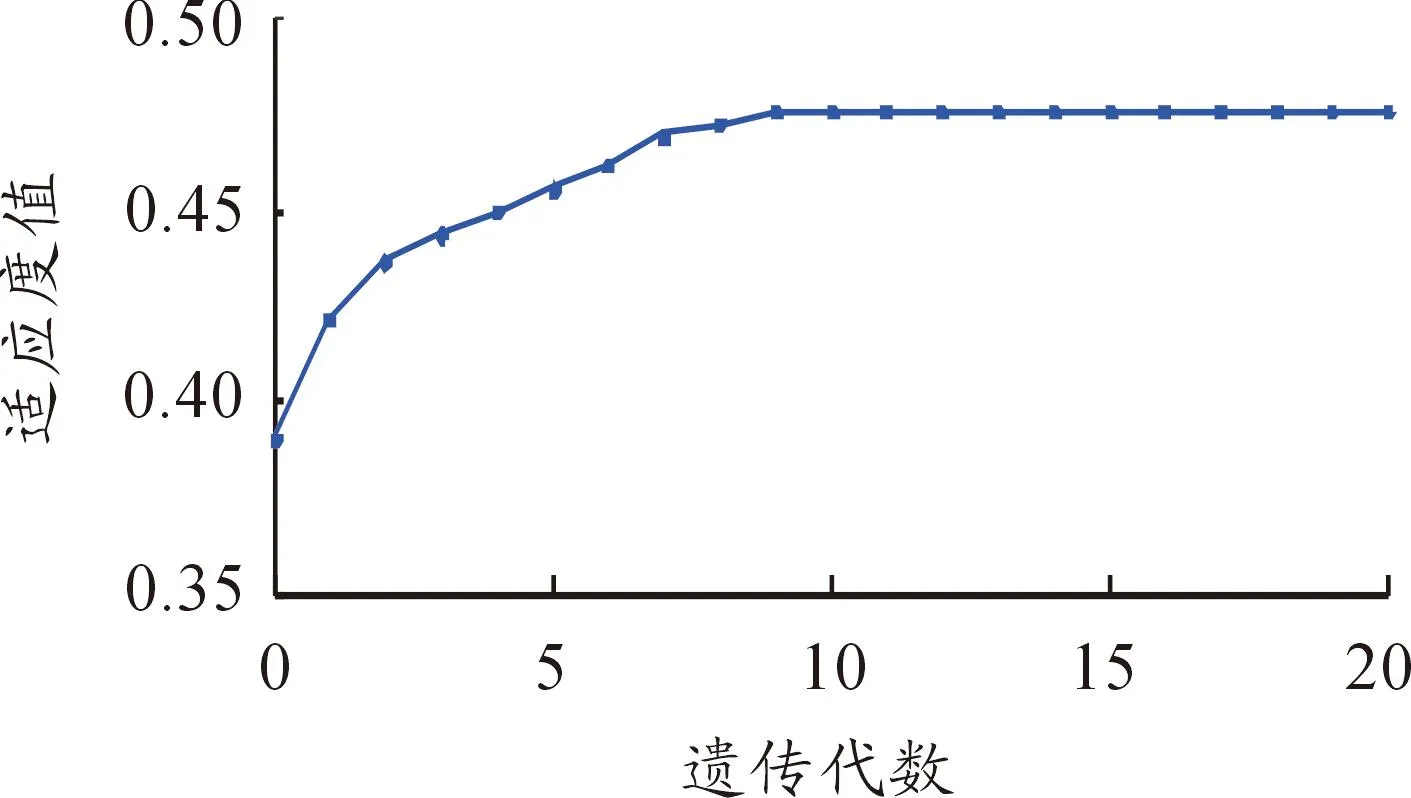
图6 适应度值变化曲线
图7 最优控制代码
3仿真结果分析
根据已建立的模型和算法,选择C级路面下的不平度来建模,车速定为40km/h,在Simulink中进行仿真,并将优化后模糊PID控制主动悬架与优化前模糊PID控制主动悬架以及被动悬架进行比较,仿真结果见图8~10。计算均方根值并进行比较,结果见表6。
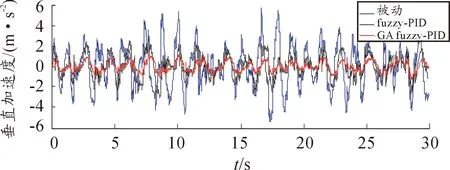
图8 加速度控制效果对比曲线
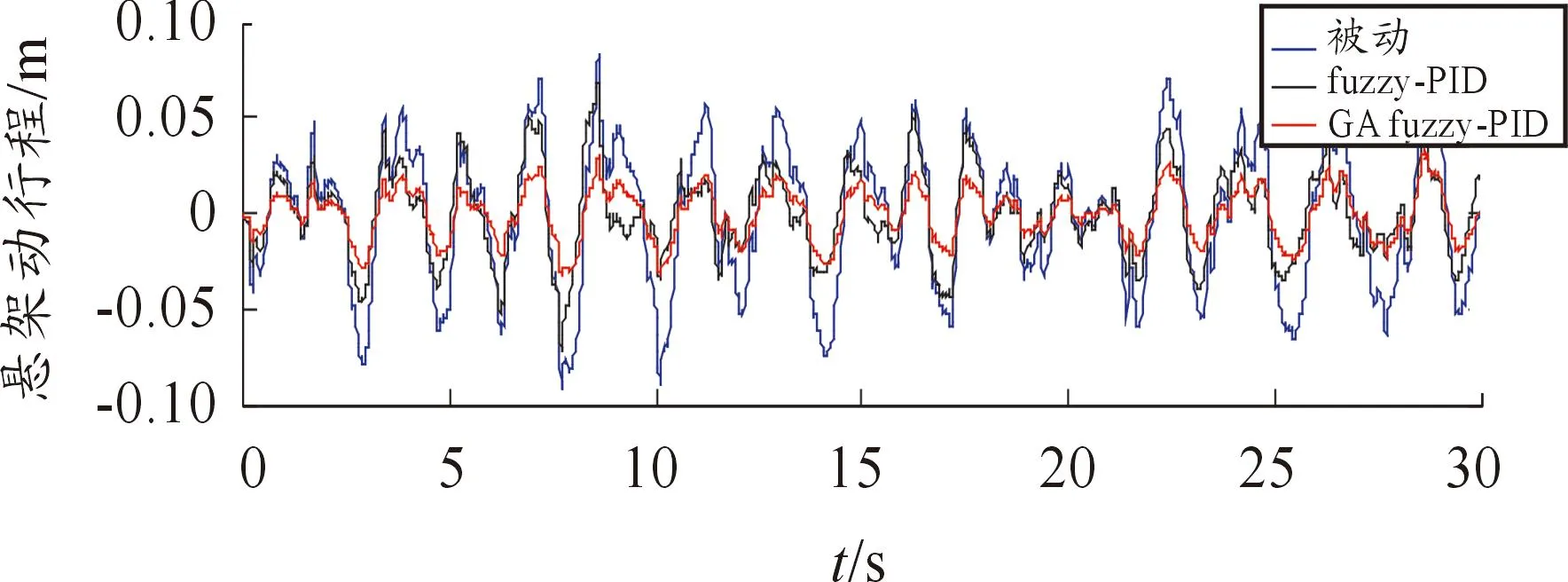
图9 悬架动挠度控制效果对比曲线

图10 轮胎动载荷控制效果对比曲线
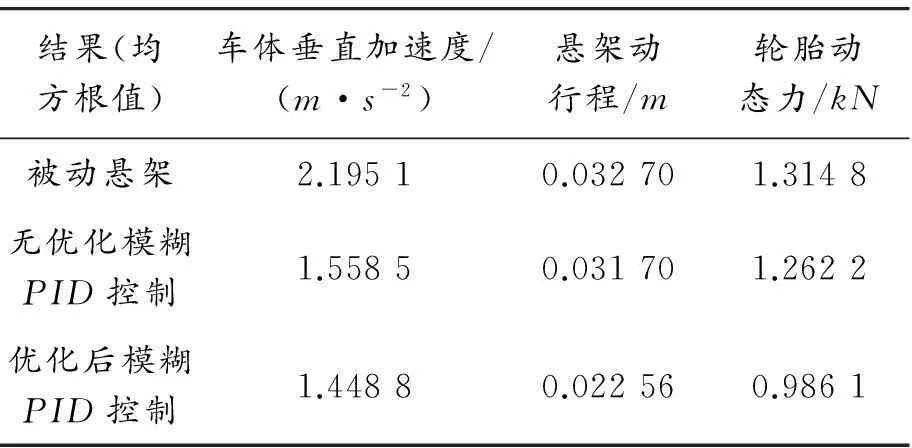
结果(均方根值)车体垂直加速度/(m·s-2)悬架动行程/m轮胎动态力/kN被动悬架2.19510.032701.3148无优化模糊PID控制1.55850.031701.2622优化后模糊PID控制1.44880.022560.9861
从表6可以看出:采用遗传算法优化模糊PID控制器的主动悬架与被动悬架相比较,车体质心垂直振动加速度减少了34%,悬架动行程减少了31%,车轮动态力减少了25%。
4结束语
采用遗传算法优化模糊PID控制器,其效果优于模糊PID控制效果,说明采用遗传算法优化模糊PID控制参数是有效的,克服了常规手动调整参数所带来的局限性。
优化后的车体质心垂直振动加速度、悬架动行程和轮胎动态力的峰值及其均方根值都有所降低,说明基于GA的fuzzy-PID控制器的主动悬架性能优于fuzzy-PID控制的主动动悬架和被动悬架,能够较好地提高车辆的乘坐舒适性。
参考文献:
[1]夏均忠,马宗坡,方中雁,等.汽车平顺性评价方法综述[J].噪声与振动控制,2012,32(4):9-13.
[2]邵亚军,高钦和,程洪杰.基于不同车速的特种车辆平顺性仿真研究[J].计算机仿真,2014,31(2):243-246.
[3]温良,杨明国,贺小峰,等.基于自适应遗传算法优化的模糊PID控制在实验轧机中的应用研究[J].机床与液压,2011,39(17):26-29.
[4]CAOJT,LIP,LIUHH.AnExtendedfuzzycontrollerforavehicleactivesuspensionsystem[J].ProceedingsoftheInstitutionofMechanicalEngineers,PartD:JournalofAutomobileEngineering,2010,224(6):717-733.
[5]SANGY,WOOKHK.Genetic-basedfuzzycontrolforhalf-caractivesuspensionsystems[J].InternationalJournalofSystemsScience,1998,2(7):699-710.
[6]王海燕,燕巍.一种自整定PID参数的模糊控制系统的设计与仿真[J].自动化技术与应用,2015,34(4):14-19.
[7]陈克,高洁净,吕周泉.基于虚拟试验场技术的汽车平顺性仿真分析[J].中国工程机械学报,2010,8(2):208-212.
[8]杨劼.求解约束优化问题的遗传算法研究[D].大连:大连海事大学,2013.
[9]王威,薛彦冰,宋玉玲,等.基于GA优化控制规则的汽车主动悬架模糊PID控制[J].振动与冲击,2012,31(22):157-162.
(责任编辑刘舸)
Fuzzy-PID Control of Vehicle Active Suspension Based on Genetic Algorithm Optimization
ZHAO Qiang1, HE Fa1, WANG Xin1, LIU Jie-xiong2
(1.Traffic College,Northeast Forestry University,Harbin 150040,China;2.Brilliance China Automotive Engineering Research Institute,Shenyang 110141,China)
Abstract:To solve the optimal parameters selection problem of fuzzy-PID controller of vehicle active suspension, genetic algorithm and its global optimization ability and parallel capacity were used to optimize the quantification factors and the correction coefficients of PID parameters. The smoothness and tire grounding were taken as the comprehensive evaluation indexes, the objective function including the body vertical acceleration, the suspension dynamic displacement and the tire dynamic load was established, and genetic algorithm was employed for the controller parameter optimization. Further the parameters of Ford Granada were selected to complete the control simulation. The simulation results show that the actively controlled chassis using the fuzzy-PID controller optimized by the genetic algorithm can have much performance improvement compared to that using fuzzy-PID without optimization and the corresponding passive one.
Key words:active suspension;fuzzy-PID controller;genetic algorithm
文章编号:1674-8425(2016)02-0006-06
中图分类号:U463.33
文献标识码:A
doi:10.3969/j.issn.1674-8425(z).2016.02.002
作者简介:赵强(1971—),男,博士后,教授,主要从事车辆动力学及其运动模拟研究;通讯作者 何法(1991—),男,硕士,主要从事车辆动力学及其运动模拟研究。
基金项目:黑龙江省留学归国人员科学基金资助项目(LC2015019)
收稿日期:2015-07-05
引用格式:赵强,何法,王鑫,等.基于遗传算法优化的车辆主动悬架模糊PID控制[J].重庆理工大学学报(自然科学版),2016(2):6-11.
Citation format:ZHAO Qiang, HE Fa, WANG Xin, et al.Fuzzy-PID Control of Vehicle Active Suspension Based on Genetic Algorithm Optimization[J].Journal of Chongqing University of Technology(Natural Science),2016(2):6-11.

