砂土地层中隧道施工引起土层沉降的颗粒流模拟研究
王正兴, 施 焱
(南通城市建设集团有限公司, 江苏 南通 226100)
砂土地层中隧道施工引起土层沉降的颗粒流模拟研究
王正兴, 施焱
(南通城市建设集团有限公司, 江苏 南通226100)
摘要:为研究隧道施工条件下土层的沉降规律,利用离散元软件PFC2D,建立隧道-土体颗粒流数值模型,模拟砂土地层隧道施工过程中的土层沉降。研究结果表明: 通过设计,颗粒流方法可有效模拟隧道施工的开挖问题;土拱效应的发挥程度与地层损失率成正比,同时土层剪应变率呈现由隧道中轴线向两侧逐渐减小、由深层向浅层逐渐展开的分布规律。分析结果可为工程实践中分析砂土地层隧道施工引起的土体沉降规律提供理论依据。
关键词:砂土地层; 隧道施工; 沉降; 颗粒流模拟; 土拱效应; 地层损失率
0引言
地铁隧道施工不可避免地会引起地面沉降,造成建筑物损毁、道路路面沉陷、地下管线破坏,引发巨大的经济损失,甚至危及人们的生命安全[1];因此,有必要针对隧道施工引起的地层沉降规律进行深入的分析研究。
目前,地铁隧道施工引起地面沉降的研究方法可归结为3类: 经验公式法[2-3]、解析法[4]以及随机介质理论[5]。经验公式法主要以Peck公式为基础,基于对不同地区施工监测数据的分析和室内模型试验成果的整理与分析而衍生的一种研究方法,具有计算参数少、地区适用性强等优点,但也存在许多值得探讨的问题[6]。现有研究表明,黏性土地层隧道施工过程中,横向地表沉降槽近似服从高斯正态分布[7-9];然而,大量工程实践监测数据表明,砂土地层中隧道施工引起的横向地表沉降槽分布形态往往与高斯正态分布有较大的出入,这就给工程实践中准确预测砂土地层隧道施工引起的地层沉降分布规律带来了困难。
本文结合具体算例,利用颗粒流软件PFC2D,模拟砂土地层中盾构隧道施工引起的地层沉降、土拱效应、内部土体应力变化等情形,分析砂土地层中盾构隧道施工引起的地层沉降规律,有助于进一步研究砂土地层中隧道施工引起的沉降规律。
1隧道施工引起地层沉降的数值模拟
数值模拟计算隧道施工引起的地层损失以及沉降问题往往利用有限单位法,其主要基于连续介质理论,难以描述土体的非连续性、散体力学特性;而PFC2D能较好地模拟散粒体(砂土)的力学变形特性。
1.1宏细观参数标定
PFC2D能利用一定的颗粒集合模拟土体宏观力学响应,但至今还没有具体的宏细观力学关系的计算公式[10],故而需要先假定细观参数。利用双轴数值试验来确定颗粒流模拟土体的参数[11],通过不断地试算,获取与宏观力学特性接近的细观参数。本文的计算模型中砂土选用福建平潭标准砂,对应的物理指标[12]为颗粒密度2.643 g/cm3,最大与最小孔隙比分别为0.848和0.519,最大与最小干密度分别为1.74 g/cm3和1.43 g/cm3。通过反复双轴数值得到土体颗粒细观参数,如表1所示。

表1 土体细观参数
1.2数值模型建立
1.2.1地层损失率控制模型
颗粒流计算隧道施工产生的地层损失率,可通过如图1所示的地层损失率控制模型来实现对不同工况条件下地层损失率的控制,其中空隙参数g表示隧道施工过程中由于超挖、盾尾间隙等因素造成的衬砌与盾构之间的空隙[13]。数值计算模型中衬砌与盾构机体均用颗粒流程序中的“wall”命令实现,盾构半径、隧道半径分别为2 m和3 m;同时,为充分研究砂土地层中由于隧道施工引起的土拱效应,本文颗粒流模型建立过程中控制地层损失率相比工程实践取值较大,分别为4.94%、9.75%和14.44%(极限条件下)。
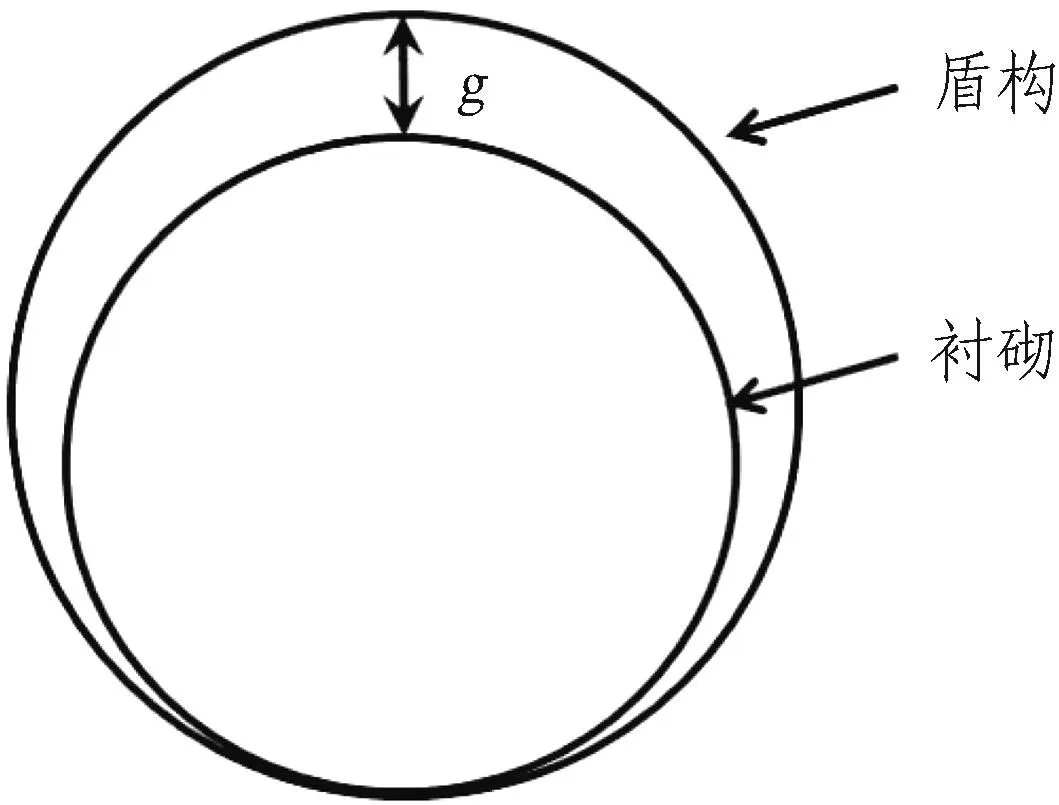
图1 地层损失率控制模型
1.2.2隧道-土体数值模型
图2为隧道-土体计算模型,模型宽度为30 m,高度为17 m。模型共计生成约2.4万个颗粒,土体最大颗粒与最小颗粒粒径比值为3,最小粒径为3 cm,颗粒间接触模型默认为线性接触模型。隧道轴线埋置深度分别为9 m和10 m,共计进行了6组数值计算。模型建立后,删除构成盾构机体的墙体,运行至模型稳定,以达到模拟隧道开挖的目的。为监控隧道施工过程中,隧道拱顶上覆土层的颗粒位移和应力变化过程,拱顶处设置半径为0.5 m的测量圆,共计403个,如图3所示。

图2 隧道-土体数值模型(隧道埋深10 m,半径3 m)
Fig. 3Distribution of monitoring circles(depth of 9 m, radius of 2 m)
1.3模拟结果分析
1.3.1位移场云图
通过开发二维颗粒流软件后处理可视程序,得到了数值模型中每个颗粒的竖向位移值和位移云图。图4是隧道半径为3 m、轴线埋深为10 m、地层损失率为4.94%时,隧道周围土体的竖向位移云图。从图4可以看出: 隧道开挖完成后,土体最大沉降区域发生在隧道轴线正上方,隧道轴线以上土层沉降较为明显;隧道拱顶上覆土层沉降形态类似楔形体的分布,最大沉降量发生在隧道拱顶上方,随着距隧道拱顶距离越远,即距地面距离越近,土体的沉降越小,而水平方向距隧道中轴线距离越远,土体的竖向沉降越小。

图4 位移云图(单位: cm)
图5是隧道半径为3 m、轴线埋深为10 m、地层损失率为4.94%时,土体颗粒的位移矢量图。从图5可以看出: 隧道开挖过程中,拱顶上覆土层位移竖向有向隧道拱顶移动的趋势,侧向有向隧道内侧扩张的迹象。显然,这是因为在隧道施工过程中,由于盾构超挖引起周边土层扰动,导致原有的应力场平衡被破坏,随着时间的推移,土体颗粒发生位移,应力场重新达到平衡。

图5 位移矢量图
1.3.2土拱效应
图6是半径为3 m、轴线埋深为10 m的隧道开挖过程中,土体颗粒法向接触力分布图。从图6可以看出: 隧道开挖过程中,伴随着土体的沉降,土体颗粒间接触力形成多个“铰链拱”;随着沉降的进一步发展,两侧接触力逐渐增大,而中间区域颗粒间的接触力有先增大后减小的趋势,总体上两侧接触力明显大于中间区域的接触力。这主要是上覆荷载向两侧土体荷载传递过程中,由于颗粒的错动,致使颗粒最大主应力由最初的竖向发生偏转,形成更有利于土体内部应力传递的土拱,进一步增大了土体侧向应力;随着沉降进一步发展,土拱拱顶逐渐向浅层移动,有逐渐向地表延伸的趋势。由此可知,土拱的发展、形成、破坏到再形成是随着土体的沉降发展而逐渐演变的。

图6 计算过程中土拱的分布
土拱效应的发挥程度一般采用土拱率来衡量,McNulty[14]定义土拱率为“土拱将荷载从一个地方传递到另一个地方的能力”,并用土拱率ρ来反映土拱效应能力的大小。
ρ=pb/(γH+qa)。
式中: pb为某处土体的土压力; γ为土体重度; H为土层埋置深度; qa为地表上覆荷载。
图7—9为不同隧道半径、埋深条件下土层的土拱率随埋深的变化。从图7和图8可看出,相同条件下地层损失率对土拱率有较大的影响,并可推知存在某一地层损失率,该情形下土层土拱率达到最大或最小值。对比图7、图8和图9可知,相同地层条件下,土拱率的发挥与地层损失率、隧道半径有着直接的关系,但地层损失率的变化明显比隧道半径对土拱率的影响要大。
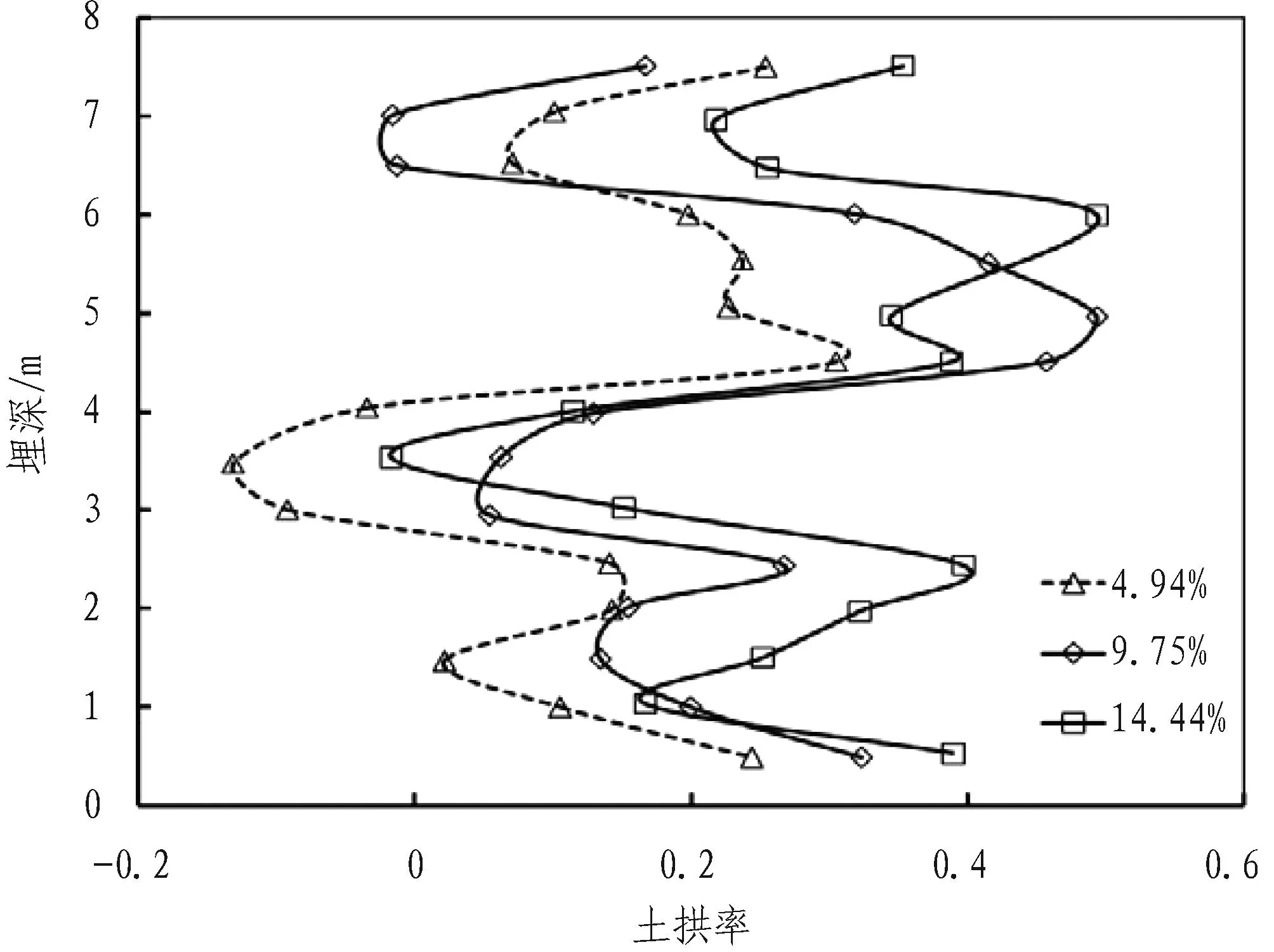
图7 土拱率随土层埋深的变化(隧道半径2 m,埋深10 m)
Fig. 7Relationshipsbetweensoilarchingratioanddepth(radiusof2m,depthof10m)
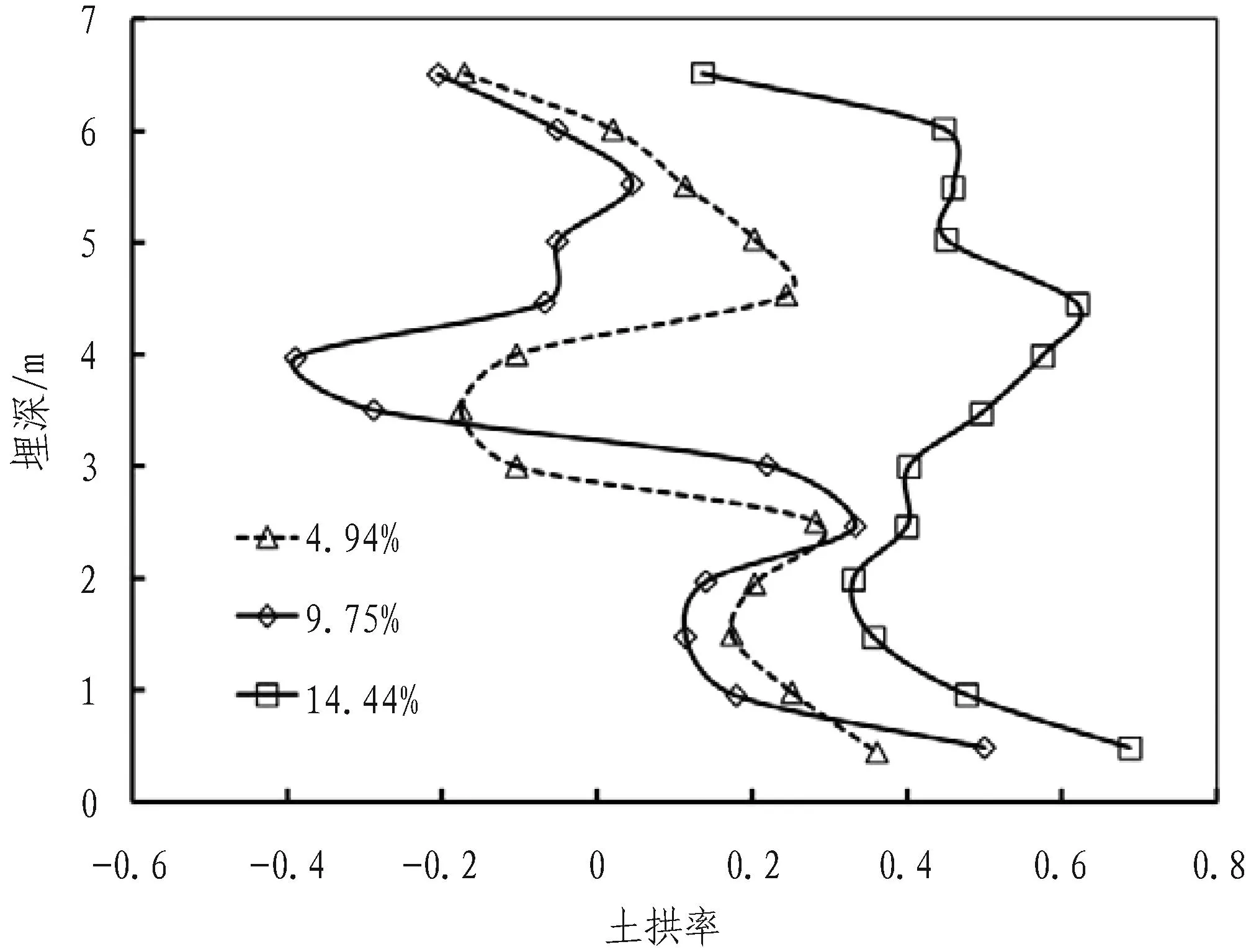
图8不同地层损失率条件下土拱率随埋深的变化(隧道半径3 m,埋深10 m)
Fig. 8Relationships between soil arching ratio and the depth in different ground losses(radius of 3 m, depth of 10 m)
1.3.3侧压力及侧压力系数
侧压力系数是衡量土拱效应发挥的一个重要参数。本文利用测量圆监测隧道轴线正上方侧压力系数随着土体沉降发展的变化。图10为隧道埋深10 m(r=3 m,地层损失率4.94%)时,隧道轴线正上方埋深6 m处土层侧压力系数变化规律。从图10可以看出: 盾构隧道开挖初期,由于隧道上覆土层应力平衡瞬间被打破,该处土层的侧压力系数数值较为离散;随着沉降的发展,侧压力系数逐渐收敛并有一定程度的增加,至土层沉降逐渐稳定,该处侧压力系数逐渐减小并趋于一稳定值。
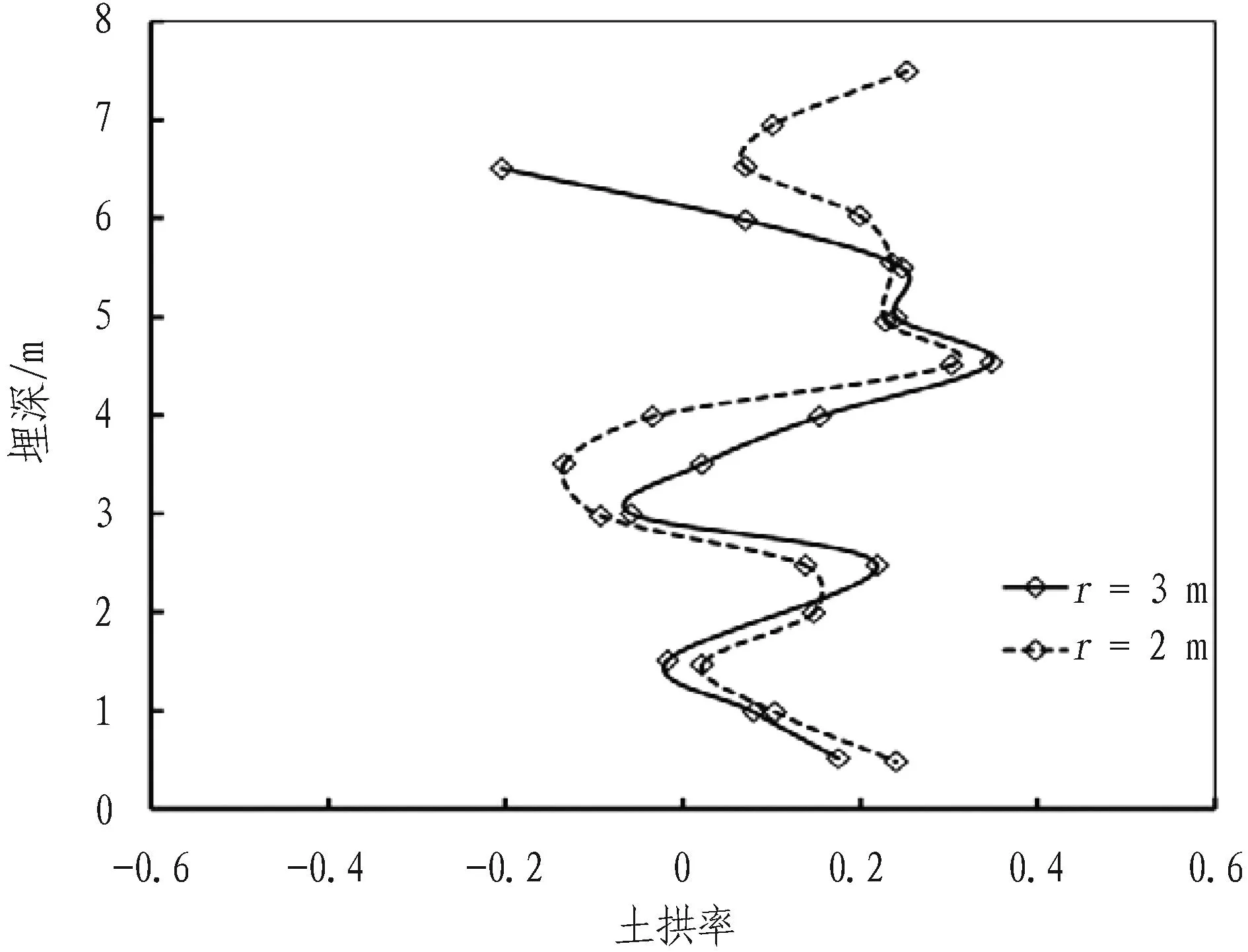
图9相同地层损失率、隧道埋深条件下土拱率沿深度的变化(地层损失率4.94%)
Fig. 9Relationships between soil arching ratio and the depth in the identical ground loss and depth(ground loss of 4.94%)

图10隧道施工过程中隧道轴线正上方(埋深6 m处)侧压力系数的变化
Fig. 10Variation of lateral pressure coefficient during calculation(in condition of 6 m depth)
图11为隧道埋深10 m(r=3 m,地层损失率4.94%)时,隧道轴线正上方埋深4 m处侧压力系数随着土体沉降发展的变化。从图11可以看出: 隧道开挖初期,土层的侧压力系数数值较为离散,随着沉降的发展,侧压力系数逐渐收敛并趋于一稳定值。对比图10和图11可知,隧道施工过程中,相同地层损失率和隧道埋深条件下,隧道轴线正上方不同埋深的土层侧压力系数变化规律有所不同,显然这是由不同层位土层土拱的形成和发展的程度不同而引起的;因此,在隧道工程相关监测过程中,一定要重视对该类现象的分析和判别。
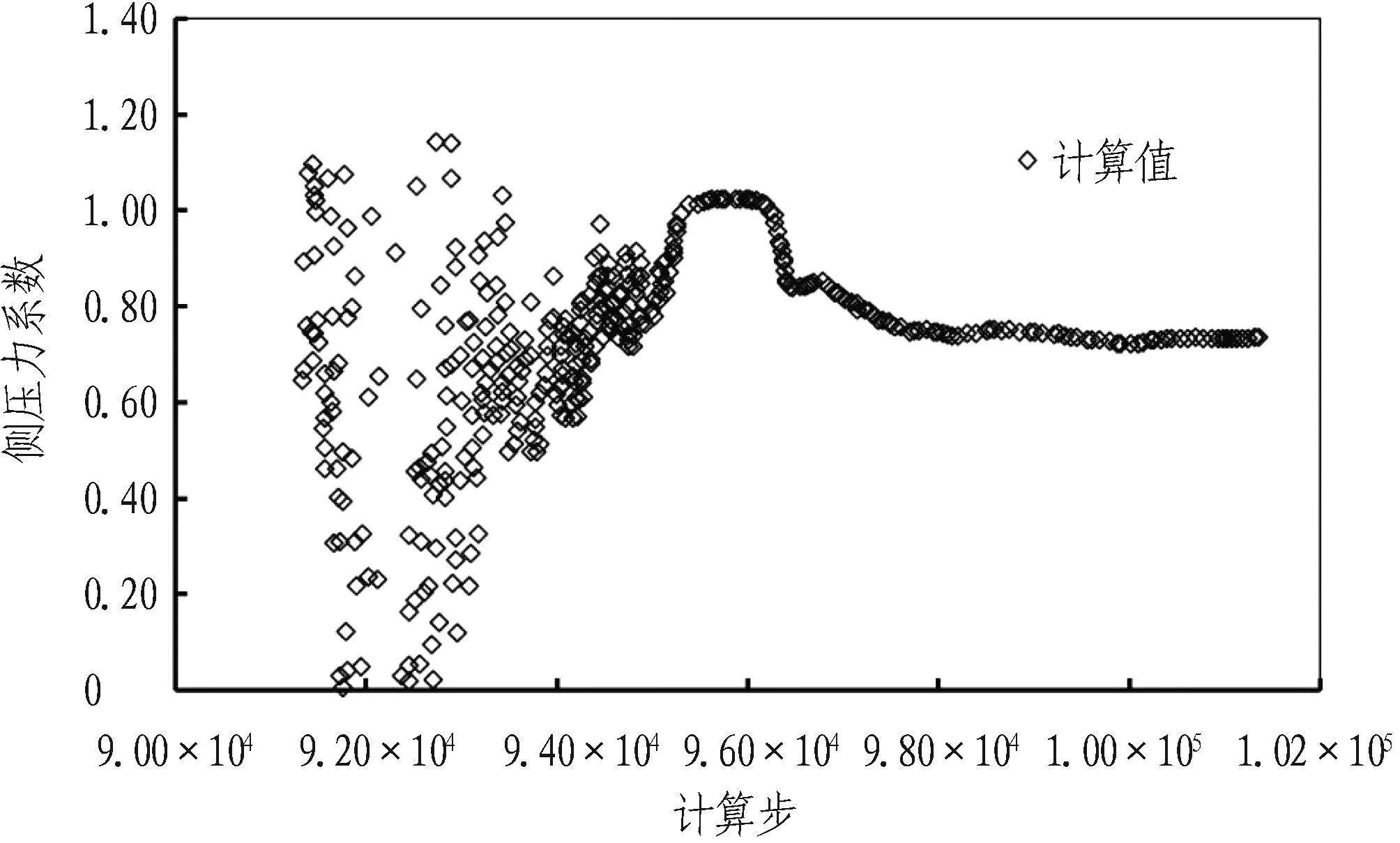
图11隧道施工过程中隧道轴线正上方(埋深4 m处)侧压力系数的变化
Fig. 11Variation of lateral pressure coefficient during calculation (depth of 4 m)
图12是隧道轴线埋深为10 m、半径为2 m、地层损失率为4.94%时,隧道开挖过程中土体竖向应力、水平应力的变化情况。从图12可以看出: 隧道开挖初期,上覆土体有一个明显的卸载过程,相应的竖向土压力和侧向土压力值极其不稳定,随着土体应力场逐渐达到平衡,应力值也趋于一稳定值;比较开挖前后竖向土压力和侧向土压力的值,可知该处隧道开挖完成后,土体应力场重新平衡后期,土体的竖向应力增长幅度明显大于侧向应力。对比图11和图12可以看出,2种不同半径的隧道,在相同地层损失率开挖条件下,土体应力场均经历如下过程: 开挖瞬间,周边土体颗粒呈现类似卸载的现象;随后竖向应力和侧向应力逐渐增加,增加的幅度基本相同,表现为侧压力系数接近1;随着颗粒应力场逐渐平衡,竖向应力增加的幅度明显大于侧压力,此时侧压力系数逐渐减小并趋于一稳定值。

图12隧道施工过程中隧道轴线正上方(埋深6 m处)土层应力的变化
Fig. 12Variation of soil stress during calculation (depth of 6 m)
1.3.4剪应变率
图13为不同地层损失率条件下隧道土体(r=2 m、埋深10 m)剪应变率分布等值线。从图13可以看出: 给定某一地层损失量条件下土层的剪应变率由隧道中轴线向两侧逐渐减小,由深层向浅层逐渐展开,至地面处土层受剪应变影响范围最大;随着土层埋深减小,相应的剪应变率也会逐渐减小,且相同条件下隧道周边土体的剪应变率与地层损失率成正比。由此可知,隧道施工引起的土体内部剪切力或相应的剪切变形对埋置于土层内部的管线、桩基础等变形有较大的影响。充分认识该规律对隧道施工过程中沿线构筑物及埋地管线的保护有着重要的指导意义。

(a) 地层损失率4.94%

(b) 地层损失率9.75%
2结论与讨论
本文利用颗粒流PFC2D软件,构建隧道-土体颗粒流计算模型,研究隧道施工条件下土体的沉降变形、土拱效应、剪应变率分布与地层损失率变化的关系,得到如下结论。
1) 在砂土地层中,当隧道开挖完成后,隧道拱顶上覆土层沉降形态类似楔形体的分布;最大沉降量发生在隧道拱顶上方;隧道上覆土体的沉降量与距隧道拱顶的距离成反比;隧道拱顶上覆土层位移竖向有向隧道拱顶移动的趋势,水平方向有向隧道内侧扩张的迹象。
2) 土拱的发展、形成、破坏到再形成是随着土体的沉降发展而逐渐演变的。相同地层条件下,土拱率的发挥与地层损失率、隧道半径有着直接的关系,而地层损失率变化明显较隧道半径对土拱率的影响要大;土层的剪应变率分布规律由隧道中轴线向两侧逐渐减小,由深层向浅层逐渐展开,至地面处土层受剪应变影响范围最大。
3) 隧道施工引起土层沉降规律的研究,近年来虽然有了一定的进展,但是目前该方面成果应用于工程实践的仅限于一些早期的经验公式法。
4) 本文虽然在揭示隧道施工引起的砂土沉降和土拱效应变化规律方面取得了一些成果,但是对土体内部沉降与土拱率的研究还不够,尤其是在定量分析方面,其影响因素多而复杂,难以用现场和室内模型试验的方法进行有效分析。因此,需要在这些方面进行更深入的研究。
参考文献(References):
[1]缪林昌, 王正兴, 石文博. 砂土盾构隧道掘进开挖面稳定理论与颗粒流模拟研究[J]. 岩土工程学报, 2015,37(1): 98-104.(MIAO Linchang,WANG Zhengxing, SHI Wenbo. Theoretical and numerical simulations of face stability around shield tunnels in sand[J]. Chinese Journal of Geotechnical Engineering, 2015,37(1): 98-104.(in Chinese))
[2]Peck R B. Deep excavations and tunneling in soft ground[C]//Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering. Mexico City: Etat Actuel Des Conaissances,1969: 225-290.
[3]张成平,张顶立,王梦恕,等. 浅埋暗挖重叠隧道施工引起的地层变形分析[J]. 岩石力学与工程学报,2008,27(增刊1): 3244-3250.(ZHANG Chengping,ZHANG Dingli,WANG Mengshu,et al. Analysis of stratum deformation induced by overlapping tunnels construction in shallow depth[J].Chinese Journal of Rock Mechanics and Engineering, 2008,27(S1): 3244-3250.(in Chinese))
[4]施成华.城市隧道施工地层变形时空统一预测理论及应用研究[D].长沙: 中南大学,2008.(SHI Chenghua.Study on time-space united calculating theory of stratum deformation for tunnel excavation in urban and its application[D].Changsha:Central South University,2008.(in Chinese))
[5]Rowe R K. The prediction of deformation caused by soft ground tunneling: Recent trends [C]//1986 Tunneling Association of Canada Annual Publication. Edmonton: Tunneling Association of Conada,1986: 91-108.
[6]王正兴,缪林昌,王冉冉,等. 砂土中隧道施工引起土体内部沉降规律特征的室内模型试验研究[J]. 土木工程学报,2014,47(5): 186-188.(WANG Zhengxing,MIAO Linchang,WANG Ranran,et al. Physical model study on subsurface settlement by tunnelling in sand[J].China Civil Engineering Journal, 2014,47(5): 186-188.(in Chinese))
[7]Attewell P B, Woodman J P.Predicting the dynamics of ground settlement and its derivatives caused by tunneling in soil [J]. Ground Engineering,1982, 36(11): 13-22.
[8]Clough G W, Schmidt B. Design and performance of excavations and tunnels in soft clay[C]//Soft Clay Engineering. Amsterdam: Elsevier Scientific Publishing Company, 1981: 569-636.
[9]Attewell P B,Glossop N H,Farmer I W. Ground deformations caused by tunneling in soil [J]. Ground Engineering, 1978, 15(8): 32-41.
[10]朱伟,钟小春,加瑞. 盾构隧道垂直土压力松动效应的颗粒流模拟[J]. 岩土工程学报,2008,30(5): 750-754.(ZHU Wei,ZHONG Xiaochun,JIA Rui.Simulation on relaxation effect of vertical earth pressure for shield tunnels by particle flow code[J]. Chinese Journal of Geotechnical Engineering, 2008,30(5): 750-754. (in Chinese))
[11]CUNDALL P A. Particle flow code in 2 dimensions[M]. Minnesota: Itasca Consulting Group,2002.
[12]周健,邓益兵,叶建忠,等.砂土中静压桩沉桩过程试验研究与颗粒流模拟[J]. 岩土工程学报,2009,31(4): 501-507.(ZHOU Jian,DENG Yibing,YE Jianzhong,et al. Experimental and numerical analysis of jacked piles during installation in sand[J]. Chinese Journal of Geotechnical Engineering, 2009,31(4): 501-507. (in Chinese))
[13]Lee K M, Kerry R, Lo K Y. Subsidence owing to tunnelling I: Estimating the gap parameter[J]. Candian Geotechnical Journal,1992,29: 929-940.
[14]McNulty. An experimental study of arching in sand[R].Vicksburg: US Army Engineer Waterways Experiment Station, Corps of Engineers,1965.
Study on Ground Settlement Induced by Tunneling in Sandy Strata Using PFC2D
WANG Zhengxing, SHI Yan
(NantongUrbanConstructionGroupCo.,Ltd.,Nantong226100,Jiangsu,China)
Abstract:A numerical model of tunnel-soil is established by means of PFC2D(Particle Flow Code) discrete element software, so as to simulate the ground settlement induced by tunneling. The study results show that: 1) The PFC2Dcan be considered as an effective way to simulate the tunnel excavation. 2) The effect of soil arch is proportional to the ground loss. 3) The shear strain rate of sandy strata decreases gradually from the medial axis to the side and increases gradually from deep soil to shallow soil during tunneling. The analysis results can provide theoretical reference for study on ground settlement induced by tunneling in sandy strata.
Keywords:sand strata; tunneling; settlement; PFC2D; soil arching effect; ground loss rate
中图分类号:U 455
文献标志码:A
文章编号:1672-741X(2016)02-0158-06
DOI:10.3973/j.issn.1672-741X.2016.02.006
作者简介:第一 王正兴(1981—),男,江苏南通人,2004年毕业于吉林大学,土木工程专业,博士,工程师,现从事盾构隧道施工对地面沉降及埋地管线性状影响的研究工作。E-mail: johnston_2002@163.com。
收稿日期:2015-08-21; 修回日期: 2015-10-25

