隧道下穿引起地下管线竖向位移的计算方法研究

王春梅， 何越磊， 汪　磊，2，*， 李培超

(1. 上海工程技术大学城市轨道交通学院， 上海　201620；

2. 上海大学土木工程系， 上海　200072； 3. 上海工程技术大学机械工程学院， 上海　201620)



隧道下穿引起地下管线竖向位移的计算方法研究

王春梅1， 何越磊1， 汪磊1，2，*， 李培超3

(1. 上海工程技术大学城市轨道交通学院， 上海201620；

2. 上海大学土木工程系， 上海200072； 3. 上海工程技术大学机械工程学院， 上海201620)

摘要：为建立盾构隧道正交下穿施工引起的管线变形计算理论，将既有管线视为连续长梁，结合横观各向同性条件下的小孔扩张理论，导出管线在下穿盾构隧道施工作用下的竖向位移计算式。结合工程实例对该计算方法进行算例验证，并在此基础上定量分析管线竖向位移与各向异性参数、隧道外径、净距、管线抗弯刚度等因素的关系。结果表明： 1)管线最大竖向位移发生在下穿正交点处； 2)各向异性参数越大，对管线竖向位移的影响越显著； 3)净距在某一范围内时，管线竖向位移对其变化较敏感，超过此范围后管线竖向位移基本无变化； 4)盾构隧道外径、管线抗弯刚度对既有管线竖向位移也有一定的影响。

关键词：横观各向同性； 下穿； 弹性地基梁； 盾构隧道； 小孔扩张； 地下管线

0引言

地铁隧道的埋深一般较小，其上部可能存在给水、排水、燃气、供热、电力之类的地下管线，隧道开挖引起的地层变形可能导致管线产生变形和承受附加应力，进而影响管线的正常使用甚至安全[1]。因此，对下穿施工作用下地下管线的变形规律进行研究，有益于早期变形预测与施工设计，同时对管线的加固防护具有一定的指导意义。

既有管线变形研究方法主要包括解析法、试验法和数值模拟法，解析方法具有严谨的推导过程和可靠的数学依据，能够为工程问题提供简单、明确的解决方法。比如： A. Klar等[2]基于Winkler地基模型推导了无限长梁在附加荷载作用下的最大弯矩解析式并将其应用于隧道开挖对已有管线的影响研究；张桓等[3]采用2阶段法建立了基于双参数Pasternak地基模型的管线变形计算方法；魏纲等[4]将Peck公式及其改进方法应用于地下管线的应力及竖向位移计算；刘晓强等[5]采用能量变分法研究了地下管线在隧道穿越施工影响下的变形规律。模型试验采用足尺或缩尺模型模拟实际工况。比如： T. Kimura等[6]进行了大量的离心模拟试验并研究了管道应力及变形与土层应力的关系；王正兴等[7]通过3组施工模型试验分析了垂直下穿隧道施工过程中砂土和管线的位移规律；王志佳等[8]研究得出了土-地下管线相互作用振动台试验的相似常数；张陈蓉等[9]采用模型试验和有限元模拟对其提出的修正Winkler地基模量表达式进行了相关验证。随着计算机技术的发展，有限元数值模拟已成为目前研究穿越问题的主要方法[10-11]。

本文基于小孔扩张理论与弹性地基梁方法，并考虑土体的横观各向同性特性，提出一种盾构隧道正交下穿施工作用下既有管线竖向位移的计算方法，旨在寻找具体的工程实际与单一力学模型之间的平衡，希望提出的计算方法能够远近得当，既具体可用，又不失一般性。

1基本假定

1)土体为横观各向同性，新建隧道正交穿越既有管线。

2)隧道断面为圆形，小孔扩张视为轴对称的平面应变问题。

3)管线结构与地基土体完全接触，隧道外侧土体与隧道协调变形。

2理论分析与计算

2.1弹性地基梁理论

将既有管线简化为弹性地基梁，如图1所示。

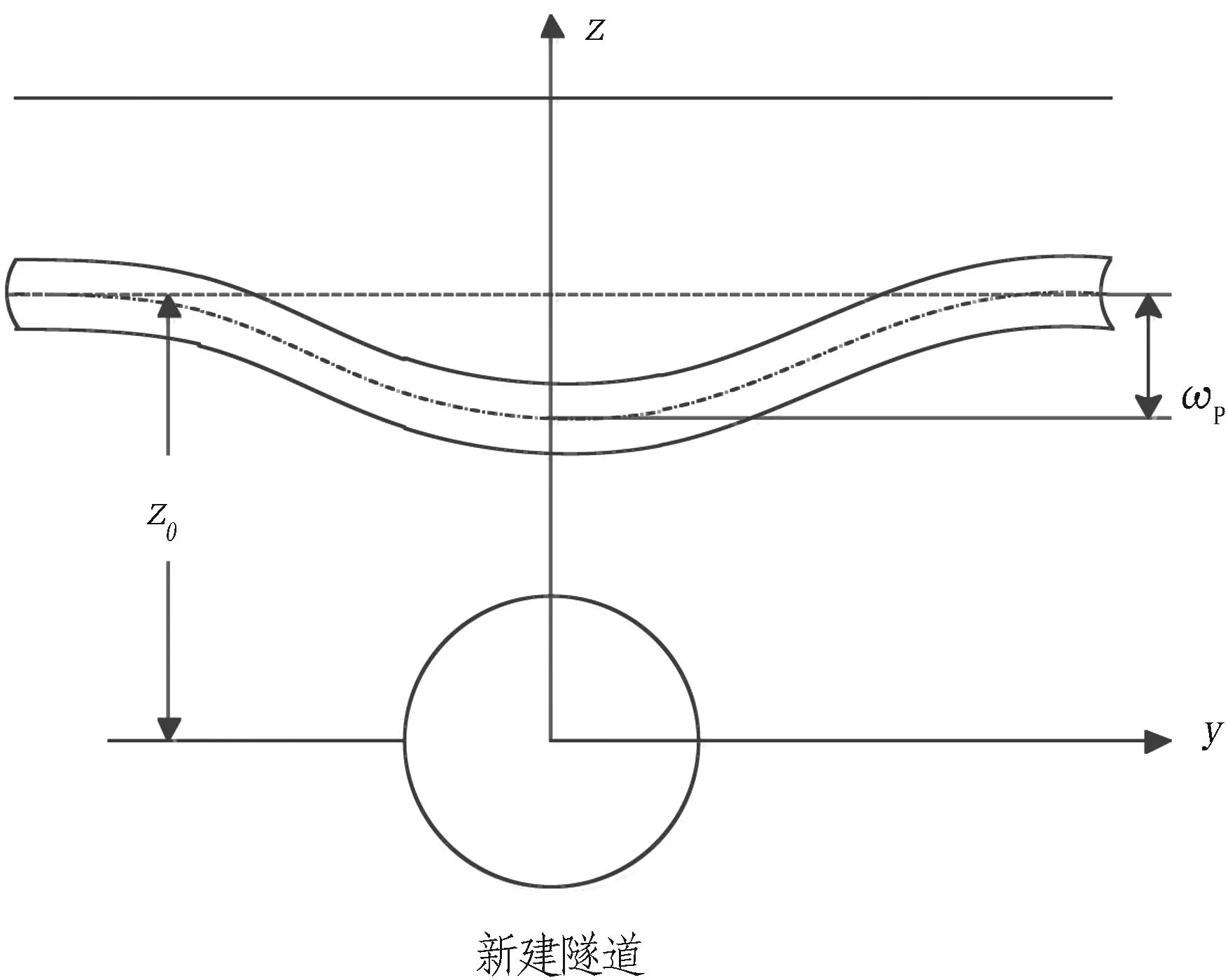
图1　弹性地基梁计算简图

则既有线路微段平衡方程[12]为

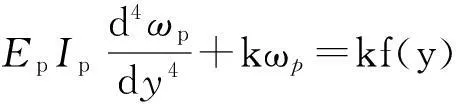
(1)

式中： EpIp为管线抗弯刚度； k为既有土体反力系数； ωp为既有管线挠度； f(y)为既有管线所处地层处的竖向变形。

对式(1)进行整理得

(2)

管线与其周围土体协调变形，则作用在既有管线上的附加应力为

-k(ωp-ω)=-k[ωp-f(y)]。

而对于梁的平面弯曲，其挠曲微分方程为

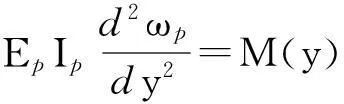
(3)

对式(3)两边分别求导得

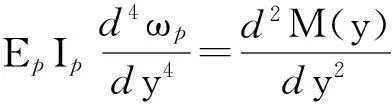
(4)

在平面弯曲问题中，有

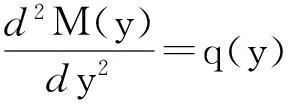
则式(4)可简化为

(5)

式(5)q(y)与式(2)k[f(y)-ωp]物理意义相同，因此可统一采用σz表示，即上述二式均可表示为

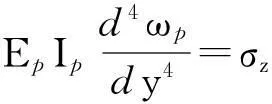
(6)

2.2厚壁圆筒扩张理论

盾构掘进过程可以看成是柱孔扩张过程[13]，如图2所示，a为小孔初始半径，在本文中实际为塑性区半径，塑性区的大小取决于隧道半径R与扩张压力p的大小。则

(7)

式中：p为盾构土舱压力与开挖面水土压力之差，p=(α-1)K0γ(h+R)(其中α为盾构土舱超压系数；K0为静止土压力系数；γ为土体重度；h为隧道埋深)；c为土体黏聚力；φ为土的内摩擦角。

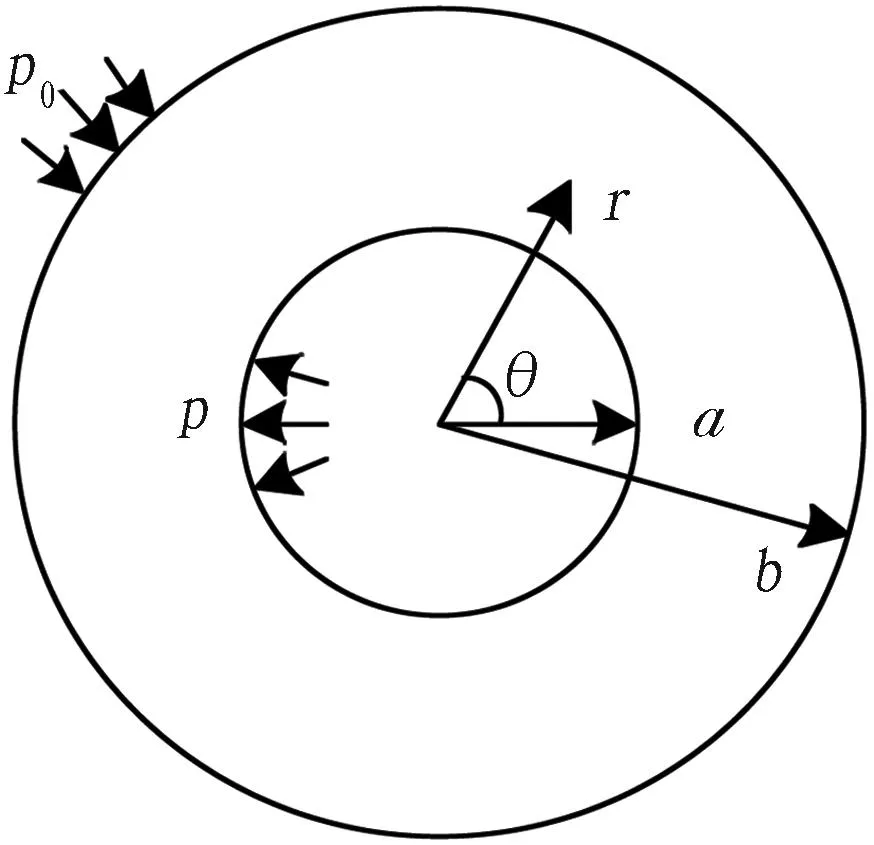
图2　小孔扩张原理示意图

横观各向同性介质有一个对称轴，与对称轴垂直的平面内各方向具有相同的弹性常数，天然土的长期自然沉积使其呈现分层的以纵向为对称轴的横观各向同性特性。横观各向同性材料中圆柱孔扩张应力解为[14]：

(8)

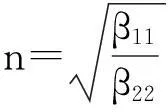
其中aij为弹性模量和泊松比的简单函数[15]，即：

式中： γ为柱孔半径； Exx、Eyy、Ezz分别为x、y、z方向的弹性模量； μ为泊松比； σr、σθ分别为径向应力和环向应力； p0为作用在无限远处的静止土压力，p0=K0γh； K0=1-sinφ。

利用弹性力学应力坐标变换公式

(9)

对式(8)进行坐标变换得：

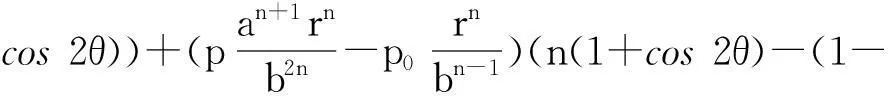
cos2θ))]。

(10)

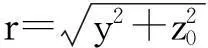
2.3基本方程及求解

综合上述理论分析，由式(10)与式(6)可得基本方程如式(11)所示。

(1-cos2θ))]。

(11)

边界条件：

y=0时， EpIpωp=Q=0，ωp=θp=0；

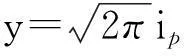
常规方法无法求得式(11)的解析解，若在实际工程中其他参数均已确定，可采用数值分析得到其近似解；但n取1即土体为各向同性时，可求得其精确解析解如下。

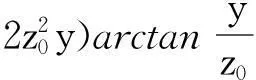
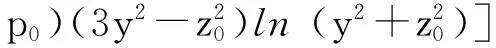
(12)

由对称性可知，管线在y=0处取得最大挠度，则其挠曲线斜率为0，故转角θp为0；又有剪力Q为0，即：

EpIpωp=Q=0，ωp=θp=0。

ωp=0,θp=0。

通过以上边界条件，即可确定隧道纵向位移ωp与各参数关系的解析表达式：

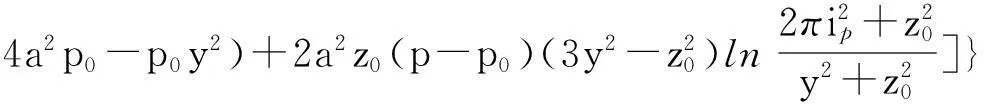
(13)

式中： ip采用经验公式[16]进行计算。对于黏性土，ip=0.43(h-zp)+1.1； 对于砂性土，ip=0.28(h-zp)- 0.1。zp为计算点与地面的距离。

3算例验证及影响因素分析

3.1算例验证

选取工程实例[17-18]进行算例验证，各参数取值如表1所示。

表1　算例中各参数取值

将上述各参数代入解析式(12)后可得既有管线的纵向位移变化规律如图3所示。

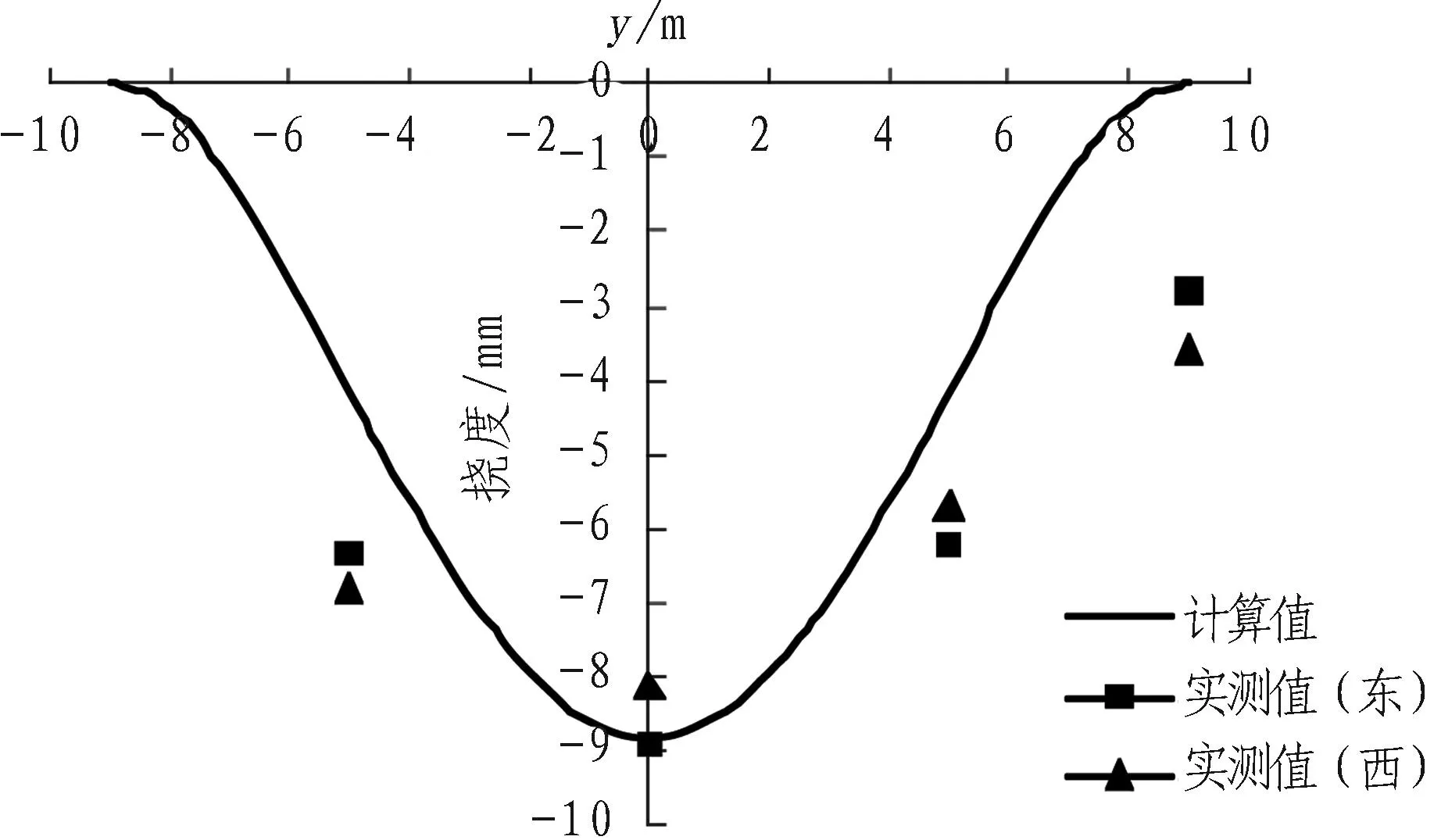
(a) 算例1中既有管线纵向挠曲线

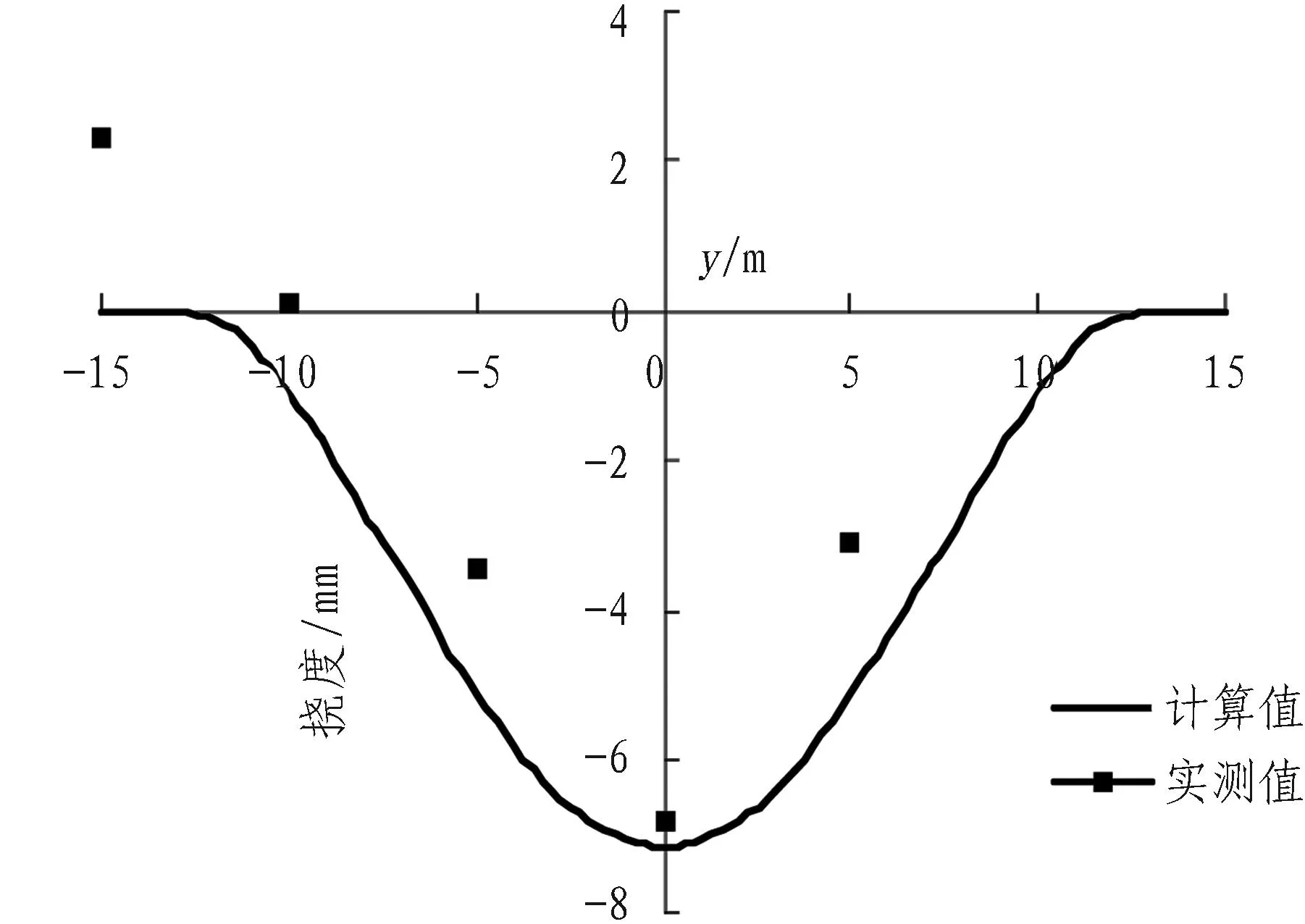
(b) 算例2中既有管线纵向挠曲线

由图3可知： 变形趋势与实测结果基本吻合，算例1中，计算所得最大竖向变形为8.808 mm，实测最大变形为8.96 mm，误差为-1.70%；算例2中，计算最大竖向变形为7.12 mm，实测最大变形为7.03 mm，误差为+1.28%。由此可见，解析解对最大变形的预测较准确。

3.2误差分析

1)算例1中，沉降槽宽度与实测值有一定差距，计算值整体小于实测值。净距z0为5.7 m，其中包含隧道半径3.0 m与管线半径1.5 m，即隧道与管线外壁间距仅为1.2 m，实际上管线有可能处于塑性区，而为简化计算，本文将问题视为完全弹性问题，有一定的偏差，且超近距离穿越时，管线变形对许多因素的变化更为敏感，例如土体的相对滑动、管土相互作用、土体孔隙水的变化、管线埋设年份等，本文未考虑上述因素。

2)算例2中，沉降槽形状与实际基本一致，计算值整体大于实测值，偏于保守。其原因是算例2中管线为变形要求较高的煤气管道，管土相互作用显著，而本文未考虑管土相互作用。需要注意的是，此类管道在下穿影响下与土体的变形协调性差(实测中y=-15 m 处有隆起)，所受的附加应力更大，若超过许用应力，管线就有破坏的危险。

3.3影响因素分析

该计算方法所得隧道变形数值中的负号仅表示方向，为使关系曲线直观而便于分析，本次参数分析图中隧道竖向位移均取正值。

3.3.1各向异性参数n

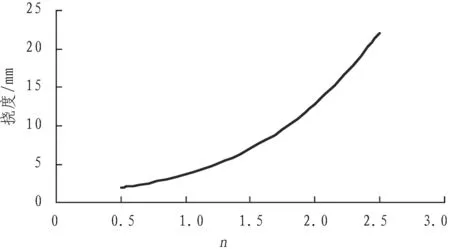
管线竖向位移与各向异性参数n的关系见图4。

(a) n取不同值时管线的挠曲线

(b) 管线竖向位移随n变化趋势

Fig. 4Relationship between vertical deflection of underground pipeline and anisotropic parametern

各向异性参数n的大小主要由μzx与μyz确定，若μzx>μyz，则n<1；若μzx<μyz，则n>1。由图4(b)可知： 管线竖向位移ωp随n的增大而逐渐增大，曲线斜率逐渐增大，说明随着参数n的增大，其对既有管线竖向位移的影响也越来越显著。传统理论分析忽略了土体的横观异性特性，对计算结果有一定的影响。

3.3.2隧道外径R

将式(13)包含的塑性半径a通过式(7)换算为隧道半径R,即可分析隧道半径取不同值时既有管线的变形情况。管线竖向位移与隧道外径R的关系见图5。

(a) R取不同值时管线的挠曲线

(b) 管线竖向位移随R变化趋势

Fig. 5Relationship between vertical deflection of underground pipeline and tunnel’s radiusR

由图5可知，图5(b)曲线斜率逐渐增大，这说明下穿隧道外径越大，对上方管线变形的影响越大，故在相同施工条件下,盾构隧道直径较大时,应注意加强防护。

3.3.3管线中心与新建隧道中心净距z0

计算选取的新建隧道外径为6 m，管线变形量与z0的关系见图6。由图6(b)可知： 净距超过15 m时管线竖向位移基本不再变化，故可认为下穿施工对管线竖向位移的影响范围约为2.5D(D为新建隧道外径)，小于交叉隧道施工的3.5D。

3.3.4管线抗弯刚度EpIp

管线变形量与EpIp的关系见图7。

由图7(b)可知，随着管线抗弯刚度的增大，管线竖向变形逐渐减小。抗弯刚度较大的管线，其抵抗弯曲变形的能力越强，相应的变形也较小，但应当注意的是，并不是变形越小管线结构就越安全，应格外注意管线承受的附加应力是否超过许用应力。管线附加应力计算简图如图8所示。

(a) z0取不同值时管线的挠曲线

(b) 管线竖向位移随z0变化趋势

Fig. 6Relationship between vertical deflection of underground pipeline and vertical distancez0

管线受到的地层压力集度为k(ω-ωp)，故抗弯刚度较大的管线承受的附加应力更大，此类工程问题应注意检算管线受力是否超限。

4结论与讨论

本文结合弹性地基梁理论及横观各向同性小孔扩张原理，提出了一种既有管线在盾构隧道正交下穿施工作用下的竖向位移的计算方法，并结合工程实例将其退化为各向同性条件下的解析式进行了算例验证，初步结论如下。

1)既有管线的最大竖向位移发生在正交点(即y=0)处，计算所得管线变形趋势与实测结果相吻合，能够较准确地预测既有管线的竖向位移；管线竖向位移随各向异性参数及隧道外径的增大而增大；管线与隧道净距较小时，既有管线竖向位移对净距的变化十分敏感，盾构施工影响范围约为 2.5D；当既有管线抗弯刚度较小时，其受盾构施工的影响较显著，但抗弯刚度大的管线承受更大的附加应力，此类管线应当注意针对其容许应力进行检算校核。

(a) EpIp取不同值时管线的挠曲线

(b) 管线竖向位移随EpIp变化趋势

Fig. 7Relationship between vertical deflection of underground pipeline andEpIp

图8　管线附加应力计算简图

2)文中计算方法将问题完全弹性化，对净距较大的穿越问题计算较准确，而近距离穿越中，由于管线可能处于塑性区，计算结果误差稍大；且由于简化后结构与荷载的对称性，计算结果也呈对称性，忽略了盾构推进的时间效应。

3)小孔扩张理论在隧道施工与设计中应用广泛，本文将小孔扩张理论与弹性地基梁理论相结合，提出了一种既有管线竖向位移的半解析计算方法，该方法对工程问题进行了适当的简化，可为工程问题提供有益参考。

参考文献(References)：

[1]赵文娟, 吴波, 白瑞雪，等. 高铁大断面隧道下穿地下管线施工安全风险管理[J]. 地下空间与工程学报, 2012, 8(增刊2): 1805-1809. (ZHAO Wenjuan, WU Bo, BAI Ruixue, et al. The risk management about high speed railway tunnelling with large section under the underground pipelines [J]. Chinese Journal of Underground Space and Engineering, 2012, 8(S2): 1805-1809. (in Chinese))

[2]Klar A, Vorster T E B, Soga K, et al. Soil-pipe interaction due to tunneling: Comparison between winkler and elastic continuum solutions[J]. Geotechnique, 2005, 55(6):

461-466.

[3]张桓, 张子新. 盾构隧道开挖引起既有管线的竖向变形[J]. 同济大学学报(自然科学版), 2013, 41(8): 1172-1178.( ZHANG Huan, ZHANG Zixin. Vertical deflection of existing pipeline due to shield tunnelling[J]. Journal of Tongji University(Natural Science), 2013, 41(8): 1172-1178. (in Chinese))

[4]魏纲, 朱奎. 顶管施工对邻近地下管线的影响预测分析[J]. 岩土力学, 2009, 30(3): 825-831.(WEI Gang, ZHU Kui. Prediction for response of adjacent pipelines induced by pipe jacking construction[J]. Rock and Soil Mechanics, 2009, 30(3): 825-831. (in Chinese))

[5]刘晓强, 梁发云, 张浩, 等. 隧道穿越引起地下管线竖向位移的能量变分分析方法[J]. 岩土力学， 2014(增刊2): 217-231.(LIU Xiaoqiang, LIANG Fayun, ZHANG Hao, et al. Energy variational solution for settlement of buried pipeline induced by tunneling[J]. Rock and Soil Mechanics, 2014(S2): 217-231. (in Chinese))

[6]Kimura T, Kusakabe O, Saitoh K. Geotechnical model tests of bearing capacity problems in a centrifuge[J]. Geotechnique, 1985, 35: 33-45.

[7]王正兴, 缪林昌, 王冉冉, 等. 砂土中隧道施工对相邻垂直连续管线位移影响的模型试验研究[J]. 岩土力学, 2013(增刊2): 143-149. (WANG Zhengxing, MIAO Linchang, WANG Ranran, et al. Model test study of vertical buried continuous pipelines displacements affected by tunnelling in sand[J]. Rock and Soil Mechanics, 2013，(S2): 143-149. (in Chinese))

[8]王志佳, 邓小宁, 姜云晖, 等. 地下管线-土相互作用振动台试验相似律研究[J]. 合肥工业大学学报(自然科学版), 2014 (9): 1108-1111.(WANG Zhijia, DENG Xiaoning, JIANG Yunhui，et al. Scale theory of soil-underground pipeline interaction in shaking table scale model test[J]. Journal of Hefei University of Technology(Natural Science)，2014(9): 1108-1111. (in Chinese))

[9]张陈蓉, 卢恺, 黄茂松. 工程堆载对市政管线纵向响应的影响分析 [J]. 岩石力学与工程学报, 2015, 34(增刊1): 3055-3061.(ZHANG Chenrong, LU Kai, HUANG Maosong. Study on the longitudinal response of municipal pipeline induced by construction load[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(S1): 3055-3061. (in Chinese))

[10]袁鸿鹄, 宫晓明, 张琦伟, 等. 水工隧洞施工对邻近既有管线影响的三维数值分析[J]. 现代隧道技术, 2012, 49(5): 60-65,72. (YUAN Honghu, GONG Xiaoming, ZHANG Qiwei, et al. 3D numerical analysis of the effects of hydraulic tunnel construction on existing pipelines[J]. Modern Tunnelling Technology, 2012, 49(5): 60-65,72. (in Chinese))

[11]赵智涛, 刘军, 王霆, 等. 地铁暗挖施工引起的管线与地层沉降关系研究[J]. 岩土力学, 2015, 36(4): 1159-1166. (ZHAO Zhitao, LIU Jun, WANG Ting,et al. Relationship between the surface subsidence and the pipeline displacement induced by Metro tunnel construction[J]. Rock and Soil Mechanics, 2015, 36(4): 1159-1166.(in Chinese))

[12]龙驭球. 弹性地基梁的计算[M]. 北京： 人民教育出版社, 1981.(LONG Yuqiu. Calculation of elastic foundation beam [M]. Beijing: Public Education Press, 1981. (in Chinese))

[13]Carter J P, Booker J R, Yeung S K. Cavity expansion in cohesive frictional soils[J]. Geotechnique, 1986, 36(3): 215-218.

[14]YU H S. Cavity expansion methods in Geomechanics[M]. AH Dordrecht: Kluwer Academic, 2000.

[15]Lekhnitskii S G. Theory of elasticity of an anisotropic body[M]. Moscow: Mir Publishers, 1981: 13-15.

[16]O’Reilly M P, New B M. Settlements above Tunnels in the United Kingdom: Their Magnitude and Prediction[C]//Proceedings of Tunnelling’82 Symposium. London: Institution of Mining and Metallurgy, 1982: 173-181.

[17]马涛. 隧道施工引起的地层位移及其对邻近地下管线的影响分析[D]. 长沙: 长沙理工大学, 2005.(MA Tao. The research of tunneling-induced ground surface movements and their influence on adjacent utilities[D]. Changsha: Changsha University of Science & Technology, 2005.(in Chinese))

[18]孙宇坤, 吴为义, 张土乔. 盾构隧道施工对邻近地下管线影响分析[J]. 中国铁道科学, 2008,29(3): 58-62. (SUN Yukun, WU Weiyi, ZHANG Tuqiao. Analysis of the effects on the adjacent underground pipelines by shield tunneling construction [J]. China Railway Science, 2008, 29(3): 58-62. (in Chinese))

Calculation Method for Settlement of Underground Pipelines Induced by Shield Undercrossing

WANG Chunmei1, HE Yuelei1, WANG Lei1, 2，*, LI Peichao3

(1.CollegeofUrbanRailwayTransportation,ShanghaiUniversityofEngineeringScience,Shanghai201620,China;2.DepartmentofCivilEngineering,ShanghaiUniversity,Shanghai200072,China；3.CollegeofMechanicalEngineering,ShanghaiUniversityofEngineeringScience,Shanghai201620,China)

Abstract:A theoretical model based on the elastic foundation beam theory and cavity expansion theory is presented, so as to calculate the vertical displacement of existing underground pipelines. And the transverse isotropic characteristics of the soil are taken into consideration. The solution is then degenerated into isotropic results and is verified by a case study. The multiple factor analysis revealed that: 1) The larger the tunnel’s radius and anisotropic parameters are, the greater the influence on the vertical displacement of the existing pipeline is. 2) The vertical clear distance z0 would have a significant impact on vertical displacement of the underground pipeline when the value of z0 is less than 2.5D. 3) The external diameter and the bending strength of the shield tunnel affect the vertical displacement of the underground pipeline a little.

Keywords:transverse isotropy; undercrossing; elastic foundation beam; shield tunnel; cavity expansion; underground pipeline

中图分类号：U 45

文献标志码：A

文章编号：1672-741X(2016)02-0186-07

DOI:10.3973/j.issn.1672-741X.2016.02.010

作者简介：第一 王春梅(1991—)，女，山东德州人，上海工程技术大学城市轨道交通学院在读硕士，研究方向为软土盾构隧道及地下工程。E-mail： chun meicoolhappy@126.com。 *通讯作者： 汪磊，E-mail: wangleiwangjiang@163.com。

基金项目：国家自然科学基金(51405287)； 上海市科学技术委员会地方院校能力建设项目(14110501300)； 上海工程技术大学研究生科研创新项目(14KY1005)

收稿日期：2015-08-17; 修回日期: 2015-11-17