基于结构化稀疏表示的海上船舶视觉建模与跟踪

史蓓蕾　张秀山　梁英杰　郭晶晶

(海军工程大学电子工程学院计算机工程系　武汉　430033)



基于结构化稀疏表示的海上船舶视觉建模与跟踪

史蓓蕾张秀山梁英杰郭晶晶

(海军工程大学电子工程学院计算机工程系武汉430033)

摘要海上船舶视频跟踪一直是视觉跟踪中的重点课题。通用的目标建模和跟踪算法不适用于海上船舶,为获得鲁棒的跟踪效果,论文结合稀疏表示的思想,首先通过不同角度复杂采样,建立了海上常见目标的基函数字典,并提出一种对字典及测试样本进行块稀疏向量生成的方法,将结构化稀疏表示算法与目标稀疏系数之间相互关联信息进行调整。在块之间相关性足够小的情况下,采用块正交匹配追踪算法,解决了适当条件下编码复杂性的最优化问题,并将论文算法首次应用于海战场目标识别跟踪,采用论文目标跟踪测试集进行测试,并与近期提出的效果较好的跟踪算法进行对比,对比实验表明论文提出的算法具有较好的鲁棒性和稳定性。

关键词目标跟踪; 结构化稀疏表示; 稀疏表示; 块正交匹配追踪

Sea Target Tracking Based on Structured Sparse Representation

SHI BeileiZHANG XiushanLIANG YingjieGUO Jingjing

(Electronic Eng. College, Naval University of Engineering, Wuhan430033)

AbstractGeneral tracking algorithms and techniques hardly can directly be used to sea target tracking, which brings difficulties to decision support. Structured sparse representation and sea target characteristics of low sampling rate, easy to block and complex feature are combined. Firstly through the complex sampling with different angles, a maritime dictionary of common objective is established, a block sparse vector generated method of dictionary and test samples is proposed. After adjusting structured sparse coefficient and target-related information, block orthogonal matching pursuit algorithm is used to solve the coding complexity optimization problem when correlation between the blocks is small enough. The structured sparse representation algorithm is firstly applied to sea target tracking. With our target tracking test set, comparative experiments show that the proposed algorithm has better robustness and stability than other recently proposed recognition algorithm.

Key Wordstarget recognition, structured sparsity representation(SSR), sparsity representation(SR), Block-OMP(BOMP)

Class NumberTP391

1引言

海上船舶视频跟踪方法对于海上交通、安全、监控和军事情报都有重要作用,一直是视觉跟踪领域的研究重点。海上环境复杂多变,目标难以采样,易受遮挡,环境(外观、姿态、光照)变化,干扰等因素影响,加大了目标跟踪难度。稀疏表示(SR)打破了传统奈奎斯特-香农采样定理(NS)的信息量度限制,提供了从少量非自适应线性测量值中恢复原始信号的方法,这一特性恰好适用于海上目标跟踪。SR理论指出在复杂多维数据空间中,目标信号只和大量样本中的部分密切相关,从而大大简化问题处理过程,因此对于图像处理和目标跟踪中高维复杂数据集处理,具有较大潜在应用和研究价值。

SR相关重要理论思想和结果来源于Candes、Tao和Donoho在数学领域的探讨和研究[1~3],包括SR算法的表述、字典学习、SR解的唯一性与稳定性和求解基本方法等。其在视觉跟踪方面的理论发展经历了标准SR[1]、鲁棒SR[4]、自适应SR[5]、结构化SR[6]、SR分类[7]、鲁棒稀疏编码[8]、正则化鲁棒编码(Regularized Robust Coding,RRC)[9]等,主要应用包括:特征表示与选取、字典学习、稀疏引导的相识度度量、稀疏编码分类框架、高维非线性学习、贝叶斯压缩感知、稀疏子空间学习等。Hong Cheng等对稀疏表示和学习在视觉对象跟踪中的理论与应用进行了综述[10]。John Wright等研究了SR理论用于人脸识别的方法,通过1-范数来优化测试样本权重系数x以及测量矩阵进行特征选择来进一步降维,确定SR的最优解。Junzhou Huang等基于编码复杂度和结构之间的关联,开发了一套SSR理论,采用StructOMP把编码方案近似的块结构来限制搜索空间,有效求出SSR的解[5]。Zhengjun Han等研究了基于样本的自适应SR(AdaSR)视觉目标跟踪,采用L1范数最小化选取样本集,并利用卡尔曼滤波器自适应计算解决外观变化和遮挡时的稀疏表示问题[11]。

以上方法存在一定的限制,或者训练库中的样本具有局限性,或者对目标遮挡效果不明显,或者难以解决目标跟踪。本文主要研究结构化稀疏表示(SSR)在海战场目标跟踪方面的应用,SSR引入了稀疏系数之间的相关性先验信息,可以提高稀疏分解算法精度,其适合任意结构的特征集。本文结合SSR特点和海战场目标特征提取算法,将SSR与目标稀疏系数之间相互关联信息和实时目标结构变化进行调整,采用块正交匹配追踪解决了在适当的条件下编码复杂性的最优化问题,可以有效解决遮挡、样本集局限性以及目标跟踪问题。

2群稀疏海战场目标特征集结构化字典学习

SR理论基本前提在很短时间间隔内,针对足够大的训练样本空间,测试样本可以由训练样本中同类的样本子空间线性表示[12]。如果测试样本由整个样本空间表示,则表示系数是稀疏的。给定y∈RL为测试样本,AT=[a1,a2,…,ad]∈RL×d(L>d)为训练样本空间,即过完备字典或基函数字典,x=(x1,x2,…,xd)∈Rd为定义在字典中每个模板的相应目标系数向量,‖x‖0≤d,则稀疏域模型描述为

y≈ATx=a1x1+a2x2+…+adxd

(1)

为解决目标跟踪中可能会遇到的遮挡问题,加入一个稀疏误差e∈RL,则观测样本y表示如下:

(2)

其中,A=[ATAe]∈RL×(d+L)是由目标模板集和遮挡模板集组成的训练样本基础库,Ae为单位矩阵。此外引入稀疏系数之间的相关性先验信息来建立稀疏相关系数ω,能够大幅度提高稀疏分解算法精度。ω∈Rd+L是一个密度非均匀稀疏系数向量,ω中误差部分e是稀疏的,稀疏向量部分x是密集的。这主要是因为大部分视频系统帧速率平均适中,目标遮挡面积随着时间而不断改变。在迭代过程中,假设ATx|t可表示目标外观模型与遮挡模型之和(即Aω|(t-1)),移动时间步长Δt遮挡引起的误差ê只占用一个稀疏空间向量。当向量x足够稀疏,目标系数x和稀疏误差e可以通过解决l0范数极小化问题共同解决。公式如下所示:

(3)

其中,‖·‖0为l0范数,代表非零项的数量,‖·‖2为l2范数,参数e表示重构误差。上式为解决欠定最小化0范数问题,解不稳定且又是NP-hard问题。在约束等距性(Restricted Isometry Property,RIP)条件下,0范数优化问题与1范数优化问题具有相同的解。l0最小化问题可以转化为l1凸优化问题等价求解,则目标模板集和相应目标系数的积与恢复图像之间,具有最小残差的图像便为跟踪结果(即argmin‖y-ATx‖2)。除此转化之外,为适应跟踪过程中外观及遮挡变化,提出一个启发式的在线模板更新方案。

虽然l1最小化能通过凸优化算法解决多项式稀疏表示问题,但计算耗时且实施复杂,很难达到实时视觉跟踪。贪婪方法,如匹配追踪(MP)和正交匹配追踪(OMP)等算法在效率、计算成本和结果方面比l0范数有优势。当训练样本基础库A和稀疏系数向量x具有块结构特点时,MP和OMP可有效解决稀疏表示问题。接下来讨论块稀疏性质以及块稀疏正交匹配追踪(BOMP)算法在视觉跟踪应用和实现问题在第5节讨论。

3从稀疏表示到结构化稀疏表示

稀疏表示的原理框架适用于目标外观和遮挡的建模,并不需要考虑稀疏系数任何先验分布。实际上,式(2)中的ω经常有一个基本的结构顺序。假如查询样本具有低于20%连续遮挡,预期的非零项都集中在目标系数向量x中,那么测试目标样本y可以更好地近似训练模板集的线性表示。另一方面,实际视觉跟踪过程中,部分遮挡通常表示为所观察目标样本一个连续的空间分布,分析图像的局部特征可以提高对未知但连续的遮挡的跟踪性能。我们采取这样的局部区域分块方法来解决部分遮挡问题,具有块稀疏表示的特点。观察到的样品与训练模板间一对一空间映射关系如图1(深颜色为遮挡部分)所示,首先把观测到的样本和训练模板按照“列分类”分别堆叠成一维向量,相应连接形成一维观察样本y和训练模板ai,i∈[1,d]。通过局部区域分析,连续遮挡可作为非零项块稀疏向量来编码。

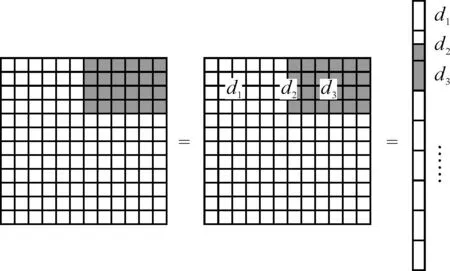
图1　块稀疏向量生成

最近对块结构稀疏来恢复阈值和提高效率的研究,取得了明显的进步。在这项工作中,我们采取上述结构稀疏表示方法,在视图中串联(R+1)相同的块,来考虑基础库A=[ATI]和稀疏系数向量ω=[xe]T(图2)。A和x分块的第一部分分别对应目标模板集A和目标相关系数X,而余下的块对应局部分区区域和它们的系数。假定,观测目标样本y在式(1)中所观察到的维数是L,块的长度是d,L=Rd(R为整数)。因此,式(2)中基础库A可以被看作是一个串联的具有相同的长度d的R的相同块的串联。加入噪声分布的块稀疏向量表示如式(4)所示:

(4)

基于块划分基本压缩感知模型(式(4))称为块稀疏模型,基础库向量A=[ATI]可以划分为d个块结构(每个块结构包含的元素有多有少),而d的非零元素聚集在少数几个块内。基于块稀疏模型,目前已经有了不少算法,比如Group Lasso[13],Block-OMP[14],Block-CoSaMP[15]等。但很少有算法考虑每个块内的元素之间的相关性(块内相关性)。

其中,ai∈RL和A[l]∈RL×d分别代表基础库A的第i个列和第l个块。因此,定义块稀疏系数向量ω为

(5)

其中,ωi、ω[l]∈Rd分别是向量x的第i个输入和第l个块。通常一个向量x如果具有至多m个非零项,则被称为向量m稀疏。稀疏性的定义中可以扩展到块稀疏。块K-稀疏向量x被定义为最多有k个ω[l]非零欧几里德范数的向量,即‖ω‖2,0≤k[12]。记为

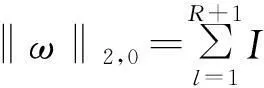
(6)

其中,I(·)是指标函数。

在文献[14]中,作者证明了正交块内的列,能够达到更高的恢复阈值。它也表明,此正交保留的块稀疏度,即如果对基础库内每个区块正交化,x中非零块的分布将不会改变。遮挡模板集是必须是单位矩阵且所有列相互正交。然而,目标模板集通常不是正交的,但具有强相关性,因为模板之间比较相似。因此,我们利用主成分分析(PCA)的方法,正交目标模板集,形成一个特征值模板来代替。

(7)

其中D=[UAe]∈RL×(d+L)是新的基础库,由构成的特征模板集U∈RL×d和最初的遮挡模板集Ae=I组成。向量a=[ce]T∈Rd+L包含对应特征模板集和遮挡模板集的分解系数,特征模板集U是通过奇异值分解(SVD)获得的:AT=U∑VT。

使用本征代替原始模板的模板可以解决文献[16]中提出的最初启发式模板更新计划。首先,原始模板子空间的稀疏表示是有限的,不能解决视角和姿态的重大变化。因为它只涉及到解决从以前的几个时间瞬间获得的模板。在基础库更新后遇到背景斑点或跟踪结果显著遮挡情况下,原型l1跟踪器是容易跟踪失败。这主要是因为在遇到背景噪音和目标遮挡后,很可能用错误的模板来表示图像以达到与图像最相似。特征模板可以解决并避免这些问题,因为它通过获得增量SVD更新程序的之前外观数据,具有学习模板相关性的能力。这个模板已经成功地运用于目标跟踪场景。自学习特征模板能够比原始模板在解决重大姿势改变时,对目标提供更丰富的描述。因为它们能够获得对当前和过去的跟踪模型都最小重构误差的最优子空间。此外,它也能够解决由之前外观信息转换成目标模板集,即错误更新而带来的漂移问题。并且,我们不采用文献[16]中的非负约束,因为PCA允许特征模板和系数是任意信号,并涉及复杂的正负数间的抵消。增加非负约束条件,可能会导致重构失败。

4块正交匹配追踪

块稀疏信号y可以从观测样本y=Dx中恢复,在块之间相关性足够小的情况下,即可以采用l1/l2混合最优化算法求解,也可以采用BOMP算法求解。考虑到块结构的稀疏表示特点,应用BOMP来更有效的解决目标稀疏表示的稀疏线性组合。BOMP算法递归地对已选择向量集合进行正交化以保证迭代的最优性,可减少迭代次数,每次迭代包括三个主要阶段:匹配阶段、估计阶段和更新阶段。BOMP和标准OMP之间主要差别是匹配阶段。BOMP选择具有最高相关性的块,而OMP选择唯一最佳匹配模板。

在估计阶段,块一旦建立之后,相应系数通过最小二乘方最小化估计求出,剩余在第三阶段更新。BOMP算法具有能够判断观测样本是否有效的辨识能力。一个有效的观察应更好地表示目标模板,而不是遮挡模板,这才能够实现与目标模板集的最高相关性。匹配阶段,从而可以作为一个分类器,通过判断目标模板集是否在第一次迭代中出现来消除异常值。另外,如果在早期阶段一旦观察到的样本被确定为异常值便终止循环,可以缩短该算法的运行时间,并同时促进视觉跟踪中的效率和准确性。在目标跟踪过程中,首先对观测样本进行分块,并初始化目标搜索窗,然后,通过l2范数表示稀疏向量系数,最后采用BMOP算法得出目标表示的线性组合,实现目标跟踪。本文的BOMP的步骤为

输入: 1) 根据图1对观测样本进行分块,建立目标的过完备字典D(本文提供的图像格式pgm,像素大小91×112),给定观测样本y。

2) 初始化其他项r0=y,s=1,a=[]。

3) 匹配阶段:根据以下公式选择一个与rs-1最匹配的块。

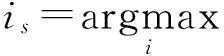
(8)

其中,D[i]为基础库D的第i个块。

3) 异值消除:如果s=1且is≠1时,中断并返回y,把y作为异值消除。

4) 估计阶段:求解最小平方问题。

(9)

其中,as[i]为矢量a的候选指数集(I=[i1,…,is])估计块系数。

5) 更新阶段:更新残差。

(10)

6)s=s+1,并回到步骤2),直到残差‖rs‖2的l2范数低于目标阈值或最大迭代次数。

输出:稀疏系数向量a。

5实验验证

我们应用这种方法在海战场目标跟中,海上数据以其数据的高维复杂性成为模式跟踪较少研究并仍未突破的难点之一。我们主要关注在两种情况下的海上目标跟踪。,

在跟踪过程中假定海上目标从图像中已经经过如检测、分割、正规化等预处理。我们在两个不同的数据库上做跟踪实验,分别是海战场背景单一、亮度差距较大且图像无损坏的场景,即只有海水为背景,噪声较少,无遮挡的情况,另一种是背景较复杂、有阴影且图像有损坏的场景,即具有天空、海水、内陆背景,船舶有阴影存在并且有遮挡情况存在的情况。前后者分别有12个不同海上的船舶,每个船舶有5张图像,总共60张图像,图像格式为pgm,像素大小为91×112,因此基础库D为m×n=10304×60的矩阵,测试图像为一维的10304×1矩阵。这些图像有不同的拍摄角度,如有的正面取景,有的则侧面取景,但角度在±15°之间。所有图像都有相同的海水背景。本文的实验环境已足够演示本文结构化稀疏表示方法的各个特性。

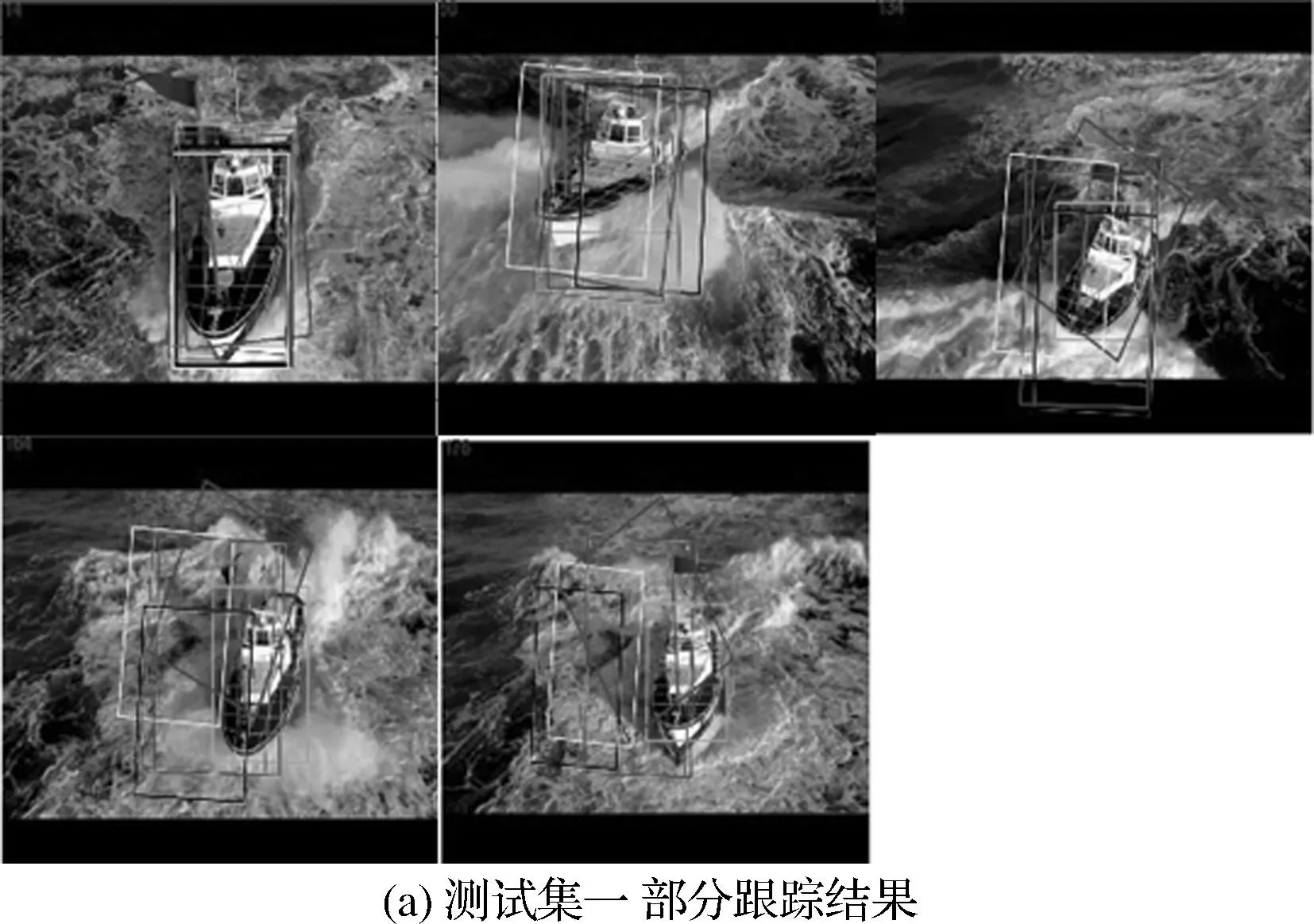
图2　结构化稀疏表示跟踪结果

为验证上述算法的有效性,本文实验的硬件环境为PC机器配置(CPU为8核Intel(R) Core(TM) i7-3770@3.40GHz,内存1×8G,显卡NVIDIA Geforce GTX660Ti),操作系统为Microsoft Windows 7专业版,32位操作系统,实验开发环境是Matlab7.12.0。本文算法部分的跟踪结果截图如图2所示,从表1统计数据可以看出,在本文采样率前期下,本文算法的检测准确率比其他跟踪算法有一定的提高。

表1　不同方法跟踪结果比较

经过120幅具有不同噪声、阴影以及云层遮挡的复杂海面船舶图像实验,结果表明特征角点法适用于图像噪声较小,目标与周围环境像素差大的跟踪环境,优点是跟踪速度快,并可直接用于跟踪;背景模型法适用于采用率高且采样角度变化较小,背景无明显变化,目标阴影不明显的跟踪环境,优点是可用于多目标跟踪。而本文算法对于遥感图像中复杂海面上的舰船检测是有效的,并且对于噪声、阴影、对比度和亮度具有很好的鲁棒性。

6结语

本文将近期提出的结构化稀疏表示方法应用于海战场目标跟踪中,通过不同角度复杂采样,建立了海上常见目标的基函数字典,并提出一种对字典及测试样本进行块稀疏向量生成的方法。将结构化稀疏表示方法与目标稀疏系数之间相互关联信息和实时目标结构变化进行调整,采用块正交匹配追踪解决了在适当的条件下编码复杂性的最优化问题,实现在在采样率较低的情况下,对海上目标的稀疏表示和准确跟踪。最后经过试验验证,本文提出的方法可以有效解决遮挡、样本集局限性以及目标跟踪问题,具有较好的鲁棒性和稳定性。

参 考 文 献

[1] Donoho D L, Elad M. Optimally sparse representation in general dictionaries via1 minimization[J]. Proceedings of the National Academy of Sciences,2003,100(5):2197-2202.

[2] Candes E J, Romberg J K, Tao T. Stable signal recovery from incomplete and inaccurate measurements[J]. Communications on Pure and Applied Mathematics,2006,59(8):1207-1223.

[3] Candes E J, Tao T. Near-optimal signal recovery from random projections: Universal encoding strategies[J]. Information Theory, IEEE Transactions on,2006,52(12):5406-5425.

[4] Wright J, Yang A Y, Ganesh A, et al. Robust face recognition via sparse representation[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on,2009,31(2):210-227.

[5] Han Z, Jiao J, Zhang B, et al. Visual object tracking via sample-based Adaptive Sparse Representation[J]. Pattern Recognition,2011,44(9):2170-2183.

[6] He L, Chen H, Carin L. Tree-structured compressive sensing with variational bayesian analysis[J]. Signal Processing Letters, IEEE,2010,17(3):233-236.

[7] Huang K, Aviyente S. Sparse representation for signal classification[C]//NIPS,2006:609-616.

[8] Yang M, Zhang D, Yang J. Robust sparse coding for face recognition[C]//Computer Vision and Pattern Recognition,2011:625-632.

[9] Yang M, Zhang L, Yang J, et al. Regularized robust coding for face recognition[J]. Image Processing,2013,22(5):1753-1766.

[10] Cheng H, Liu Z, Yang L, et al. Sparse representation and learning in visual recognition: Theory and applications[J]. Signal Processing,2013,93(6):1408-1425.

[11] Huang J, Zhang T, Metaxas D. Learning with structured sparsity[J]. The Journal of Machine Learning Research,2011,12(11):3371-3412.

[12] Donoho D L, Tsaig Y, Drori I, et al. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit[J]. Information Theory,2012,58(2):1094-1121.

[13] Meier L, Van De Geer S, Bühlmann P. The group lasso for logistic regression[J]. Journal of the Royal Statistical Society: Series B(Statistical Methodology),2008,70(1):53-71.

[14] Eldar Y C, Kuppinger P, Bolcskei H. Block-sparse signals: Uncertainty relations and efficient recovery[J]. Signal Processing,2010,58(6):3042-3054.

[15] Baraniuk R G, Cevher V, Duarte M F, et al. Model-based compressive sensing[J]. Information Theory, IEEE Transactions on,2010,56(4):1982-2001.

[16] Mei X, Ling H. Robust visual tracking using1 minimization[C]//Computer Vision, 12th International Conference on. IEEE,2009:1436-1443.

中图分类号TP391

DOI:10.3969/j.issn.1672-9722.2016.01.012

作者简介:史蓓蕾,女,硕士,讲师,研究方向:模式识别,可视化。张秀山,博士,教授,研究方向:虚拟仿真。梁英杰,博士,讲师,研究方向:模式识别。郭晶晶,硕士,讲师,研究方向:可视化。

收稿日期:2015年7月7日,修回日期:2015年8月27日