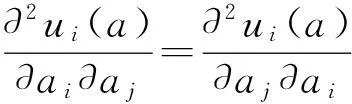基于博弈论的认知无线电网络频谱分配研究

倪秋芬

(广州华立科技职业学院　广州　511325)



基于博弈论的认知无线电网络频谱分配研究

倪秋芬

(广州华立科技职业学院广州511325)

摘要认知无线电(Cognitive Radio,CR)由于其动态分配频谱资源特性,能帮助认知用户在不影响授权用户的条件下伺机地使用某段空闲频谱,实现授权用户与认知用户之间频谱资源的共享,解决了对不可再生频谱资源再利用的问题。论文构建了基于博弈论的认知无线电频谱分配模型,并对基于博弈论的认知无线电频谱分配模型从合作博弈和非合作博弈两大类进行了阐述,最后对已有的九种博弈论模型在频谱分配方面的相关研究做了总结和归纳。

关键词认知无线电; 频谱分配; 博弈论

Spectrum Allocation of Cognitive Radio Based on Game Theory

NI Qiufen

(Guangzhou Huali Science and Technology Vocational College, Guangzhou511325)

AbstractDue to its characteristics that allocating the spectrum dynamically, cognitive radio can help the cognitive users using the idle spectrum under the condition without affecting the authorized users to realizes the spectrum resource sharing between authorized users and cognitive users, the problem of reusing of the non-renewable spectrum is solved. The model of cognitive radio spectrum allocation is constructed based on game theory, and expounding the model of cognitive radio spectrum allocation based on game theory from the cooperative game and non-cooperative game two categories. Finally, the existing nine game theory models are summarized and concluded in the research concerning the spectrum allocation.

Key Wordscognitive radio, spectrum allocation, game theory

Class NumberTN925

1引言

频谱资源由各个国家频谱权力部门采用固定频谱分配方式将无线频谱资源分配给已授权的无线接入网,造成了频谱资源在时间和空间上的极度浪费,导致频谱利用率低下[1]。

认知无线电(Cognitive Radio,CR)被用来解决对不可再生频谱资源再利用的问题。认知无线电能够智能地感知无线通信环境,实时自适应地调整系统的工作参数,使通信系统在时间及空间上对频谱进行高效共享和多维复用[2]。频谱分配根据需要接入系统的节点数目和该节点的服务要求将频谱分配给一个或多个指定节点。而系统的容量、频谱利用率和该系统能否满足用户因不同业务而不断变化的需求都是由频谱分配策略来直接决定的[6]。

2博弈论简介

2.1合作博弈

应用合作博弈论方法来研究认知无线电网络中的频谱分配问题已有很多。文献[27]中将用合作博弈来解决在认知无线电中频谱分配的过程描述如下:接入频谱之前,认知用户会先签订一个关于频谱的使用协议,按照这个协议的规则,能保证认知用户通过合作所得到的收益比单独行动获得的利润要高,在合作博弈的过程中,可以用核仁来测试认知用户之间的合作稳定与否。认知用户如何分配合作的收益问题是用夏普利值来考虑的,该值会兼顾平均和公平;当涉及到最大化最小公平原则时,认知用户合作收益的问题就要用核仁来分配。

匹配博弈(Matching Games)是一种最常见的合作博弈模型,该模型广泛地应用于很多领域的研究之中。将匹配博弈模型应用到频谱分配中时,市场的双边分别为用户和信道来进行匹配。在认知无线电网络中,空闲信道信息由频谱感知技术获得,认知用户传递给基站各自所感知到的频谱信道的信息。根据各认知用户传递过来的信道信息,基站计算出认知用户的数量和可用信道偏好,对于如何分配信道数量给各认知用户则依据匹配博弈算法。

也有将匹配博弈模型用于认知无线电频谱分配中的相关研究,文献[32]中,为了使得认知系统频谱的管理更加合理,用基于POMDP(Partially Observable Markov Decision Processes)模型的强化学习方法分析次要用户和信道状态的时变特性,构建了基于匹配博弈(Matching Games)的频谱分配模型。认知用户自适应地调整各自匹配策略,依据的就是对历史信息的观察,以及对最大化系统报酬的统计。仿真结果表明,该方法可以实现频谱资源的有效配置。

2.2非合作博弈

首要用户出租频谱给次要用户来获得一定的收益,所以首要用户之间存在一个对频谱出租的竞争关系,而次要用户之间对于租借频谱也是竞争的关系,所以,首要用户之间及次要用户之间一般都是自私非合作地获得自己最大的效用。因此用非合作博弈来研究认知无线电网络中的频谱分配是极为有效的方法。

非合作的博弈论模型主要有古诺博弈模型(Cournot Games)、伯川德博弈模型(Bertrand Games)、斯坦克尔伯格博弈模型(Stackelberg Game)、重复博弈(Repeated Games)、潜在博弈模型(Potential Games)、超模博弈模型(Supermodular Games)、拍卖博弈模型(Auction Games)、进化博弈模型(Evolutionary Games)共八种。

2.2.1古诺博弈模型(Cournot Games)

古诺博弈模型中,博弈参与者以产量作为竞争的目标。竞争过程是完全信息静态博弈。文献[33]用古诺博弈模型考虑了在进行频谱分配时,首要用户之间非合作而自私的行为。在文中,作者假设首要用户出售频谱的价格是相同的,但数量却不相同。某一个首要用户对于其它首要用户是如何出售频谱的策略都是已知的,这点就体现了古诺模型的完全信息的特性。首要用户根据各自所获得的历史信息来决定自己此时所应该采取的策略,经过了重复多次的博弈,群体中所有的首要用户所出售频谱的总数量会达到一个稳定的状态。在古诺博弈模型中,使用最大化首要用户效应函数的方法来达到授权系统频谱数量实现最大化出售量的目的。

2.2.2伯川德博弈模型(Bertrand Games)

伯川德博弈模型中,博弈参与者以价格作为竞争目标。竞争过程是完全信息静态博弈。文献[25]用伯川德博弈模型考虑了在进行频谱分配时,首要用户之间非合作而自私的行为。由于伯川德博弈模型属于完全信息的范畴,所以首要用户在博弈过程中知道其他首要用户在出售给次要用户频谱时的要价,即对历史信息的已知。然后根据其他首要用户的出价来决定自己在此时应该出售频谱的价格。经过了重复多次的博弈,群体中所有的首要用户所出售频谱的价格会达到一个稳定的状态,即为纳什均衡。在伯川德博弈模型中,使用最大化首要用户效应函数的方法来达到授权系统频谱出售价格实现最优化的目的。

2.2.3斯坦克尔伯格博弈模型(Stackelberg Games)

斯坦克尔伯格博弈[37~38]模型中,博弈参与者以产量作为竞争目标,竞争过程是完全信息动态博弈。该模型被文献[39]用来研究首要用户在进行频谱分配时,相互之间自私而非合作的竞争。在该模型中,所有首要用户在将频谱出售给认知用户时,要价是相同的,但每个首要用户可以决定自己出售多少数量的频谱给认知用户。在每次博弈过程中,一些首要用户会先采取策略,而另外一些首要用户会后采取策略,这一点正体现了“动态”的特征。这一点与前面所讲的两种博弈模型不同。由于斯坦克尔伯格博弈是完全信息动态博弈,所以,后决定出售价格的那部分首要用户总是知道先出售了频谱的首要用户的要价,这也体现了“完全信息”的特性。由于信息的透明性,首要用户就能很好地决定自己当前应该出售的频谱定价。经过了重复多次的博弈,群体中所有的首要用户所出售频谱的数量会达到一个稳定的状态,即为纳什均衡。在斯坦克尔伯格博弈模型中,使用最大化首要用户和认知用户效应函数的方法来达到授权系统频谱出售总量最大化的目的。

斯坦克尔伯格博弈模型与古诺模型有一些相同之处,比如二者的首要用户和次要用户的效用函数是相同的,还有传输系统的调制模型也是相同的。由于斯坦克尔伯格博弈模型属于动态博弈,所以它的先动优势会在频谱分配算法里有所表现,在稳定状态下,先行动出售频谱给认知用户的首要用户将比后出售频谱给次要用户的首要用户所出售的频谱数量要大。由斯坦科尔伯格博弈的特点可知,该模型适用于首要用户的行动顺序有先后之分的情况,而属于静态信息的伯川德博弈模型和古诺博弈模型则适用于首要用户同时采取行动的情况。

2.2.4重复博弈模型(Repeated Games)

重复博弈模型中博弈者采取策略是有先后次序之分的,即该模型属于动态博弈,在信息的完全性上则比较灵活,有完全信息的情况也有不完全信息的情况。重复博弈由多个博弈阶段组成,每个阶段的博弈形式是相同的,但在重复博弈的某一次博弈中可能会出现合作博弈的情况。重复博弈已被充分地应用,文献[42]考虑在有多个首要用户和一个次要用户的分布式认知无线电网络中,用博弈模型提出了一个基于首要用户空闲概率的效用函数。首要用户可以通过重复博弈调整学习速率实现纳什均衡。模拟显示,该方法使首要用户的空闲概率更大,系统效用更高,当由首要用户提供的频谱是完全空闲时系统的效用最大。此外,当首要用户的利润总额没有最大化时纳什均衡是无效的。最后合作最优解决方案可以获得最高的系统利润。

2.2.5超模博弈(Supermodular Games)

文献[44]中讲到超模博弈有弱FIP属性,例如,从一个原始行动向量开始,有一连串的“自私”行为,通过自适应的方式变化使博弈达到稳定状态,最终收敛于纳什均衡。超模博弈中存在一个特别的最佳响应序列,该序列可使博弈最终收敛于纳什均衡[44]。Topkis不动点定理[46]告诉我们,所有的超模博弈都至少存在一个纳什均衡点。而且,假如认知无线电出现了一些错误,抑或认知无线电根据对之前行为的观察,会得到一个平均权重,然后根据这个平均权重做出最佳响应,最后整个过程都会收敛于纳什均衡[44,47]。

文献[50]对认知无线电网络中几种不同的博弈模型下算法的收敛性逐个作了分析,接着文中还详细探讨了基于严格位势博弈及超模博弈等比较特殊的博弈论模型的频谱分配问题,并给出了相应的频谱分配算法。

2.2.6潜在博弈(Potential Games)

对于潜在博弈,使满足严格潜在博弈条件:

(1)

在式(1)中,当P取最大值时,这个点即是潜在博弈的纳什均衡点,潜在博弈有FIP性质,因此当各节点理性而自私地进行策略的选择时,必定会收敛到一个纳什均衡。文献[49]在分析认知无线电中分布式自适应信道分配行为时就用到了潜在博弈理论。其分配模型是这样设定的:在认知无线电网络中,在场景中均匀地分布着N个认知用户收发对,它们的收敛速度相对于所提算法而言,可以看作是静止或缓慢运动的。场景中有K个可用频谱,满足K

(2)

证明该效用函数存在一个严格潜在函数P,满足式(1)。而纳什均衡的求解方法可以参考文献[50],假定每个局中人都能清楚地知道对手策略信息。博弈参与者以最大化下一次博弈过程的效用函数为目标,通过观察对手采取的策略,来决定自己的最优策略,不断地重复博弈过程,最终达到纳什均衡状态。

2.2.7拍卖博弈(Auction Games)

认知无线电网络中,次用户想要租借频谱时,就会向拥有授权的首要用户发出对频谱租用的请求,首要用户收到了次用户发出的请求后,会决定以多少价格将空闲频谱租出给次要用户通信使用;由于次用户对租用哪一个主用户的频谱有选择权,而多个主用户相互竞争,通过价格战来吸引次要用户。但主用户在定价的同时还要兼顾自身的利益,这个过程就称为主用户之间的竞价博弈。主用户之间对价格进行拍卖博弈,通过频谱的出售使主用户得到了额外的效用,同时次用户也实现了信息的传输。使频谱实现了共享,同时频谱利用率也提高了。

文献[55]研究了认知无线电网络中的多媒体流问题,在网络中有一个首要用户和N个次要用户。文中将频谱分配问题看成一个拍卖博弈,提出了三个基于拍卖的频谱分配方案,在三个方案中频谱分配分别使用单一对象pay-as-bid升序时钟拍卖(ACA-S),传统升序时钟拍卖(ACA-T),替代升序时钟拍卖(ACA-A)三种方法。作者证明三个算法都收敛于一个有限数量的时钟。文中还证明ACA-T和ACA-A是cheat-proof,而ACA-T不是的。此外,文中表明,ACA-T和ACA-A能最大化社会福利,而ACA-S可能不会。因此,ACA-A是一个能很好地解决多媒体认知无线电网络的方案,因为它可以以一种cheat-proof的方式达到最大的社会福利。最后,通过仿真实验验证了提出算法的优点。

2.2.8进化博弈(Evolutionary Games)

作为博弈理论的新发展,进化博弈论[57~58]以生物进化论和遗传基因理论为基础[59]。进化博弈论更加贴近现实生活,假定博弈参与者是“有限理性”的,只了解部分信息,他们经过一系列的动态调整过程,如学习、试验、模仿等来渐渐适应外界环境的变化。

文献[60]中提出一种认知无线电网络中基于进化博弈的频谱分配算法,首要用户租赁他们的空闲频谱给次要用户,次要用户之间对有限频段资源相互竞争。在进化博弈过程中,不同群组内次要用户通过对自身频谱选择策略的调整以实现进化。当某一认知用户在本周期内观察并发现其选择接入当前频段所获得的收益低于群组内全体用户的平均收益,该用户将选择接入其他可用频段,即进行自身策略的调整。到下一周期,认知用户就会模仿群组内其他用户好的频谱选择策略来增加自身的收益。同时,认知用户经过多次学习,不断调整各自的策略,最后达到一个策略的均衡,也即频谱选择的进化均衡状态,这时一个群组中的每个认知用户的收益都相同。首要用户通过相互之间的价格竞争获得他们的最佳效用。仿真表明提出的算法优于主用户的均衡价格和效用。

3性能分析

而对于合作博弈和非合作博弈中的九种模型各自适用的范围及优缺点,总结如表1所示。

4结语

本文阐述了将博弈论引入到认知无线电频谱分配的研究中,描述了用博弈论来分析认知无线电中频谱分配的方案,文中将基于博弈论的频谱分配问题模型分为合作博弈模型和非合作博弈模型,并对合作博弈模型中的匹配博弈模型和八种非合作博弈模型进行了相关研究的总结和阐述。而每个模型所适合研究的问题有所不同,我们要根据所要分析的问题选择合适的模型。博弈论为认知无线电的频谱分配提供了一个很好的方法,但是这个方法还处于起步阶段,没有完善的理论系统,可以应用的博弈论模型也很有限,基于博弈论的认知无线电频谱分配问题还有很多需要解决。

表1　九种模型的适用范围及优缺点

参 考 文 献

[1] Federal Communication Commission. Spectrum Policy Task Force[R]. Report of ET Docket no. 02-135,2002.

[2] Simon Hay kin. Cognitive Radio: Brain. Empowered Wireless Communications[J]. IEEE Journal Oil Selected Area in Communication,2005:201-220.

[3] Keith Nolan. Cognitive Radio W G Brussels 2005[R]. SDR forum. Brussels,2005.

[4] Dusit Niyato, Ekram Hossain. Competitive Pricing for Spectrum Sharing in Cognitive Radio Networks: Dynamic Game, Inefficiency of Nash Equilibrium, and Collusion[J]. IEEE journal on selected areas in communications,2008,26(1):192-202.

[5] Ekram Hossain, VijayBhargava. Cognitive Wireless Communication Networks[J]. SPringer Science Business Media, LLC 2007:231-267.

[6] Chengquan An, Liu Yang. A Matching Game Algorithm for Spectrum Allocation Based on POMDP Model[C]//7thInternational Conference on Wireless Communications, Networking and Mobile Computing(WiCOM),2011:1-3.

[7] Dusit Niyato, Ekram Hossain. A Game-theoretic Approach to Competitive Spectrum Sharing in Cognitive Radio Networks[C]//Wireless Communications and Networking Conference(WCNC),2007:16-20.

[8] Zhang, T., Chen, W., Han, Z., et al. Hierarchic Power Allocation for Spectrum Sharing in OFDM-Based Cognitive Radio Networks[J]. IEEE Transactions on Vehicular Technology,2014:1.

[9] Yi Xu, Shiwen Mao. Stackelberg Game for Cognitive Radio Networks with MIMO and Distributed Interference Alignment. Vehicular Technology[J]. IEEE Transactions on Volume: 63,2014:879-892.

[10] Dusit Niyato, Ekram Hossain. Optimal Price Competition for Spectrum Sharing in Cognitive Radio: A Dynamic Game-Theoretic Approach[C]//Global Telecommunications Conference, IEEE,2007:4625-4629.

[11] Shuai Liu, Yutao Liu, Xuezhi Tan. Competitive Spectrum Allocation in Cognitive Radio Based on Idle Probability of Primary Users[J]. Youth Conference on Information, Computing and Telecommunication, IEEE,2009:178-181.

[12] Friedman, James W., Claudi Mezzetti. Learning in Games by Random Sampling[J]. Journal of Economic Theory vol. 98,2001:55-84.

[13] Topkis, Donald M. Supermodularity and Complementarity[M]. Princeton University Press, Princeton, New Jersey,1998.

[14] Milgrom, Paul, John Roberts. Rationalizability, Learning, and Equilibrium in Games with Strategic Complementarities[J]. Econometrica,1990,58(6):1255-1277.

[15] Nie Nie, Cristina Comaniciu. Adaptive Channel Allocation Spectrum Etiquette for cognitive radio networks[J]. First IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks,2005:269-278.

[16] James O. Neel, Jeffrey H. Reed, Robert P. Gilles. Convergence of cognitive radio networks[C]//Wireless Communications and Networking Conference,2004:2250-2255.

[17] Yan Chen, Yongle Wu, Beibei Wang, et al. Spectrum Auction Games for Multimedia Streaming Over Cognitive Radio Networks[J]. IEEE Transactions on Communications,2010:2381-2390.

[18] Xu Chen, Jianwei Huang. Evolutionarily Stable Spectrum Access[J]. Mobile Computing, IEEE Transactions on, Volume: 12,2013:1281-1293.

[19] Jiang, Chunxiao, Chen, Yan, Gao, Yang, et al. Joint Spectrum Sensing and Access Evolutionary Game in Cognitive Radio Networks[J]. Wireless Communications, IEEE Transactions on Volume: 12,2013:2470-2483.

[20] T. L. Vincent, J. S. Brown. Evolutionary Game Theory[M]. Natural Selection, and Darwinian Dynamics. Cambridge Univ. Press,2005.

[21] Qingyang Song, Jianhua Zhuang, Lincong Zhang. Evolution Game Based Spectrum Allocation in Cognitive Radio Networks[C]//Wireless Communications, 7th International Conference on Networking and Mobile Computing(WiCOM),2011:1-4.

中图分类号TN925

DOI:10.3969/j.issn.1672-9722.2016.01.023

作者简介:倪秋芬,女,硕士,研究方向:计算机网络。

收稿日期:2015年7月11日,修回日期:2015年8月24日