复杂社会网络节点重要性研究
姚 静 赵彤洲
(1.武汉工程大学智能机器人湖北省重点实验室 武汉 430073)(2.武汉工程大学计算机科学与工程学院 武汉 430073)
复杂社会网络节点重要性研究
姚静1,2赵彤洲1,2
(1.武汉工程大学智能机器人湖北省重点实验室武汉430073)(2.武汉工程大学计算机科学与工程学院武汉430073)
摘要复杂网络中的关键节点对整个网络有重要影响。论文分别对无向图、有向图中的网络节点进行研究,采用接近中心度、介数中心度和节点重要度等参数作为评估无向图的度量指标,而对有向图采用PageRank作为评估指标。实验数据采用某微博上获取的数据构造了一个网络结构,通过对结构相似的有向图和无向图计算结果对比,发现上述度量指标都能很好地对关键节点进行评估,进一步证实了算法的有效性和可靠性。
关键词复杂网络; 关键节点; 接近中心度; 介数中心度; PageRank
Node Importance in Complex Social Networks
YAO Jing1,2ZHAO Tongzhou1,2
(1. Hubei Provincial Key Laboratory of Intelligent Robot, Wuhan Institute of Technology, Wuhan430073)
(2. School of Computer Science & Engineer, Wuhan Institute of Technology, Wuhan430073)
AbstractThe key modes play a major role in the complex social networks. The undirected graph and directed graph are focused on respectively in this paper, which use closeness centrality, betweenness centrality and key degree to describe the important node of the undirected graphas well as thePageRank index describes the directed graph. The data from the micro-blog website is collected to construct a network. The results show the validity and reliability of these evaluating indicators.
Key Wordscomplex networks, key nodes, closeness centrality, betweenness centrality, PageRank
Class NumberTP301
1引言
复杂网络中的关键节点对整个网络有重要影响。例如,若想最小代价完成特定任务并且取得最大满意度,可对关键节点施加影响。在互联网世界中,若网络关键节点遭受攻击则会以较小代价对整个网络产生较大程度的破坏,反之,我们也可以通过保护这些关键节点提高网络的安全性。随着社交网络的快速发展,在此基础上形成的服务、应用等呈现出高度复杂化趋势,因而对其中节点的重要性进行评价进而发现其中的关键节点具有重要意义。
在复杂社会网络的研究对象是人与人或人与组织之间的关系。一个社会网络图由节点和边构成,其中,节点是现实中参与社会活动的个人或组织等单元,边是指活动参与者之间的关系[1~2]。常见的社会网络包括合作者网络、电子邮件网络和互联网社区等,在(移动)互联网世界中,国内的微博、微信、国外的Facebook中的用户及其相互关系构成了规模较大的复杂社会网络。
复杂网络的理论研究是以图论和拓扑学为研究基础的。常用的节点重要性评价方法是对节点的中心度作为度量指标。中心度的主体对象可以是网络中的节点、边、局域社团甚至是整个网络。目前常用的中心度度量指标包含节点中心度、接近中心度、介数中心度、特征向量中心度等[3~4]。著名的PageRank算法是类似于特征向量中心度的算法,这两者都包含了反馈机制。
2节点重要性评价指标
本文重点关注随机网络,即以ER随机图理论为主要理论依据的网络。复杂网络可以表示为G=〈V,E〉,其中V={v1,v2,…,vn}为顶点集合,E={ei=(vi,vj)|vi,vj∈V}为边的集合。
2.1接近中心度
接近中心度是用来度量该节点通过整个网络对其他节点产生影响的能力,若该节点的中心度越大,则该节点在网络中所发挥的作用越大,定义为
(1)
其中,dij表示节点vi,vj之间的最短距离。
2.2介数中心度
介数中心度被定义为经过节点的所有最短路径的比例[4]:
(2)
其中,pse表示从顶点vs到顶点ve之间的所有最短路径的数目,psie表示在pse中经过节点的数目。由该表达式可知,介数中心度Cb(i)实际上是评估经过该节点流向另外节点的概率。
2.3节点重要度
在接近中心度和介数中心度基础上,综合上述两种因素,定义节点重要度为
(3)
2.4PageRank
PageRank算法是基于反馈的特征向量中心度算法[5]。该算法通过计算网页之间的链接关系,从而判断网页的重要程度。其主要思想是若网页有链接指向网页时,我们称之为网页的出链,则网页将得到分数,该分数取决于网页的重要程度。当刚刚开始时,PageRank赋予每个网页相同的得分,经过一段时间迭代后网页重要性程度将通过结算结果看出。该指标被描述为[6~7]
(4)
其中,PR(i)为节点i的PageRank值,L(j)为节点j链出网页的数量,q为孤立网页的修正值。
3算法实现
3.1接近中心度算法
由接近中心度算法模型可知,该算法只需要构造节点之间的距离矩阵,距离矩阵中的元素dij即为式(1)中的分母。
3.2介数中心度算法
1) 首先用Dijstra算法计算节点vi到网络中所有其他节点之间的最短路径,并记载每个出现在路径上的节点,凡是在最短路径上的节点,其出现次数即为PSIE(i),有
2) 计算节点vi到网络中所有其他节点之间的路径(非最短路径),并记载每个出现在路径上的节点,凡是在此路径上的节点,其出现次数即为PSE(i),有
3.3PageRank算法
1) 构建邻接表,其中第一列为链接源页面,另一列为链接目标页面;
2) 用步骤1)中的邻接表构造邻接矩阵,其中的行为源页面,列为目标页面;
3) 将步骤2)中的矩阵转换为概率矩阵(转移矩阵);
4) 通过递归计算或者直接计算矩阵的特征值计算函数。
4实验结果
本文以新浪微博的数据为例进行节点重要性评估[8~9]。所有新浪微博注册的账户及其相互关系构成了一个复杂的社会网络,可以认为某一个微博账户就是网络中的一个节点,其“关注”值是该节点的出度,其“粉丝”值是该节点的入度。在评价某一账户的重要程度时,我们基于如下假设:若节点被其他节点“关注”程度值越高,则该用户越重要;若关注该节点的“粉丝”越重要(即PR值越高)则该节点越重要[10~11]。
本文以图1为例进行节点重要性评价。在图1中共有8个节点,9条边;图2有8个节点,5条单向边,4条双向边。

图1 简单社交网络拓扑结构图(无向图)

图2 简单社交网络拓扑结构图(有向图)
根据前文描述的节点重要性评价指标,构造图1的该邻接矩阵和图2的邻接矩阵,其中A中的元素表示路径(vi,vj)经过该点的次数。


计算A的psie及pse为
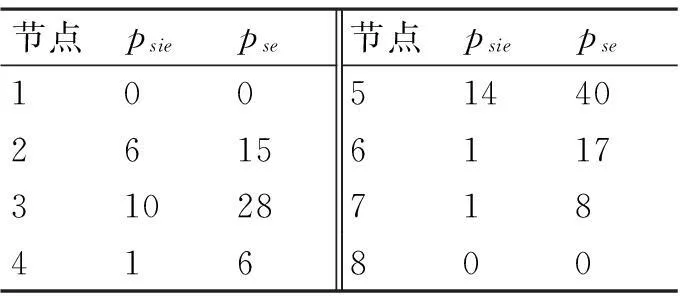
表1 矩阵A的psie及pse值
又,考虑到用PageRank算法,其中B的状态转移矩阵为PB:

由此可得计算结果如表2所示。
表2中的结果计算表明,对于无向图1节点5的重要度最高,其次是节点3,这种重要性与图的拓扑结构所反映出的保持一致,因为节点5处于整个网络的中枢位置;对于有向图2,节点5的重要程度最高,这也与图2反映的情况一致。

表2 节点重要性度量指标的比较
5结语
本文针对无向图及有向图分别用不同度量指标进行对比分析,对于无向图,运用接近度中心数、介数中心数及节点重要度判定指标,能准确地发现重要节点;对于结构类似的有向图,运用PageRank同样能发现处于关键位置的节点。因而,通过计算结果能证明上述度量指标的有效性和可信性。
参 考 文 献
[1] 仇丽青,陈卓艳.基于Pagerank的社会网络关键节点发现算法[J].软件导刊,2014,13(8):25-28.
CHOU Liqing, CHEN Zhuoyan. The key node discovery algorithm in social networks based on Pagerank[J]. Software Tribune,2014,13(8):25-28.
[2] 周涛,柏文洁,严钢.复杂网络研究概述[J].物理学报,2005,(1):79-83.
ZHOU Tao, BO Wenjie, YAN Gang. Description of complex networks[J]. Journal of Physics,2005,(1):79-83.
[3] Freeman L. Centrality in social networks conceptual clarification[J]. Social Networks,1979(3):215-239.
[4] Barabasi A L, Albert R. Emergence of Scaling in Random Netwoks[J]. Science,1999:286,509.
[5] 黄慎.复杂网络节点重要性算法研究[D].武汉:中国科学院武汉物理数学研究所,2014.
HUANG Shen. The algorithm research of node importance in the complex networks[D]. Wuhan: Wuhan Institute of Physics and Mathematics, Chinese Academy of Sciences,2014.
[6] Larry Page, Sergey Brin. The Pagerank Citation Ranking: Bringing Order to the Web[C]//Stanford Digital Libraries Working Paper,1998.
[7] Bryan K, Leise T. The $25,000,000,000 igenvector: The linear algebra behind Google. SIAM Rev.48,569,2006.
[8] Berkhin P. Asurvey on PageRank computing. Int. Math.2,73,2005.
[9] 谭跃进,邓宏钟.复杂网络中节点重要度评估的节点收缩方法[J].系统工程理论与实践,2006,(11):79-105.
TAN Yuejin, DENG Hongzhong. The node importance evaluation of node contraction method in the complex networks[J]. System Engineering Theory and Practice,2006,(11):79-105.
[10] http://open.weibo.com/.
[11] 蔡建超,蔡明.搜索引擎PageRank算法研究[J].计算机应用与软件,2008,25(9):59-60.
CAI Jianchao, CAI Ming. Search engine algorithm based on Pagerank[J]. Computer Applications and Software,2008,25(9):59-60.
中图分类号TP301
DOI:10.3969/j.issn.1672-9722.2016.01.020
作者简介:姚静,女,硕士研究生,研究方向:数据处理。赵彤洲,女,副教授,研究方向:图像处理。
收稿日期:2015年7月6日,修回日期:2015年8月26日

