多解绝对值方程的对分搜索法

王爱祥

(常州工学院机械与车辆工程学院,江苏常州213032)

多解绝对值方程的对分搜索法

王爱祥

(常州工学院机械与车辆工程学院,江苏常州213032)

绝对值方程可以作为研究线性规划、二次规划等优化问题的统一框架。针对绝对值方程具有多解的情形，提出一个基于区间数学的求解算法。在一个较大的范围内，不断将区间对分和删除，搜索到绝对值方程的每一个解。最后，数值算例也验证了算法的有效性。

绝对值方程；多解；区间算法；Krawczyk算子

0 引言

考虑如下形式的绝对值方程：

(1)

绝对值方程(1)形式简单，为研究线性规划、二次规划等众多优化问题提供了一个统一框架，引起了不少学者的研究兴趣。目前研究重点主要集中在绝对值方程(1)的性质、求解算法两方面。

在性质研究方面，Jiri Rohn在文献[1—2]中研究了绝对值方程(1)和区间线性方程组的关系，给出了绝对值方程的分类定理，证明了其等价于线性互补问题。Mangasarian在文献[3]中指出绝对值方程等价于双线性规划、广义线性互补问题，在一定条件下，绝对值方程可以转化为线性互补问题，从而得出了绝对值方程有解、无解、唯一解、非负解及多解的充分条件。文献[4]进一步研究了绝对值方程和线性互补问题的转化方法，研究了绝对值方程和混合整数规划之间的关系。文献[5—7]也研究了绝对值方程解的存在性条件。

在求解算法方面，Mangasarian在文献[3]中，证明了绝对值方程(1)是NP-hard问题，通过用有限步的逐次线性化方法求解绝对值方程(1)等价的凹极小化形式。文献[8]提出了求解绝对值方程(1)的广义牛顿法。文献[9]给出了求解绝对值方程(1)的二次收敛的牛顿法。王海军、王爱祥等在文献[10—11]中给出了求解绝对值方程(1)的区间算法和区间膨胀算法。雍龙泉等利用智能算法的优点，在文献[12—14]中分别给出了求解绝对值方程(1)的粒子群算法、和声搜索算法、差分进化算法等，取得较好的数值效果。

然而，绝对值方程(1)还存在多解或无解的情形。此时，上述文献中的牛顿型算法将无法实现，而智能算法，有时收敛性又无法保证。基于此，本文利用区间数学的工具，提出了绝对值方程(1)具有多解时的求解算法，无解时也可以判断。该算法具有很好的数值稳定性。理论分析和数值算例都验证了算法的有效性。

1 区间数学

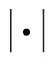
对于[x]，[y]∈I(Rn)，我们依分量也可定义中点、宽度、绝对值等概念。

定义区间运算：

[x]∩[y]=([x]i,∩[y]i)

以及

[x]⊆[y]⟺[x]i⊆[y]i，i=1,2,…,n

设区间函数F:I(Rn)→I(R)和函数f:Rn→R，对任意的xi∈[x]i，i=1,2,…,n，

F([x1,x1],[x2,x2]，…,[xn,xn])=f(x1,x2,…,xn)成立,

则称F为f的区间扩展。有关区间数学的其他概念和详细内容，参阅文献[15]。

2 Krawczyk算子

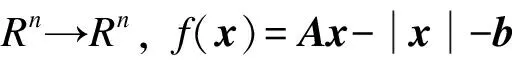
F([x])=(A-G([x]))[x]-b，

(2)

式中：G([x])=diag(G([x])1；G([x])2,…,G([x])n)；

于是F′([x])=A-G([x])。

定义Krawczyk算子为K(y,[x])=y-f(y)+(E-YF′([x]))([x]-y)，∀y∈[x]，其中E为单位矩阵。

定理1 设x*为绝对值方程(1)的解，且x*∈[x]，则对于任意y∈[x]，x*∈K(y,[x])。

证明 由x*为绝对值方程(1)的解知，f(x*)=0，x*=g(x*)。

对于任意y∈[x]，i∈(1,2,…,n)，

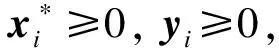
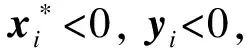
故，g(x*)∈g(y)+(E-Y(A-G([x])))([x-y])成立，即x*=g(x*)∈K(y,[x])。证毕。

根据定理1，若绝对值方程(1)的解x*∈[x]，则[x]∩K(y,[x])≠∅。我们可得定理2。

定理2 若[x]∩K(y,[x])=∅，∀y∈[x]，则绝对值方程(1)在[x]中无解。

定理3 若存在K(y,[x])⊆[x]，∀y∈[x]，则绝对值方程(1)在[x]中有解。

证明 对于任意x∈[x]，成立g(x)∈K(y,[x])⊆[x]。即连续映射g将[x]映射到自身。由于[x]为有界闭凸集，则由Browuer不动点原理得，连续映射g在[x]中有不动点存在，即绝对值方程(1)在[x]中有解。证毕。

由此，我们构造Krawczyk区间迭代法

(3)

式中：k=0,1,2,…；yk∈[x]；E为单位矩阵。

定理4 区间迭代(3)中，若对某个y∈[x]，K(y,[x])⊆[x]成立，且

wid(K(y,[x]))

对于任意x0∈[x]为初值，通过点迭代

xk+1=xk-Yf(xk)，k=0,1,2,…,

(4)

得到收敛到x*的序列{xk}。

证明 对于某个给定的y和[x]，记K=K(y,[x])和R=E-Y(A-G([x]))，显然存在0≤β<1，满足wid(K)≤β·wid([x])。

记绝对值方程(1)在[x]中的解集为Z。由定理3知，Z非空。构造区间迭代算法

下面用归纳法证明Z⊆[x]k， wid([x](k))≤βkwid([x])，k=0,1,2,…。

事实上，对于k=0，上式成立。假设上式对k=m(m>0)成立。

[x](m)⊆[x]，就有A-G([x](m))⊆A-G([x])。于是，对于ym∈[x](m)，K(ym,[x](m))⊆V(m)。由Z⊆[x](m)，有Z⊆K(ym,[x](m))⊆V(m)，故Z⊆[x](m+1)。

βmwid(Ki)≤βm+1wid([x]i)

即，wid([x](m+1))≤βm+1wid([x])。这就证明了对于k=m+1，原式也成立。

从而，当k→+∞时，wid([x](k))→ 0。

由Z非空知，序列{[x](k)}收敛到一个点x*。即，绝对值方程(1)有唯一解x*。

下面考虑由式(4)定义的迭代序列{[x](k)}，当任意点xo∈[x]，有xk∈[x]k，k=0,1,2，…。

事实上，当k=0，上式成立。假设对k=m(m>0)，上式成立，即xm∈[x]m。从而，

xm+1=xm-YF(xm)∈K(ym,[x]m)⊆Vm。

由xm∈[x]，有xm+1=xm-Yf(xm)∈K(y,[x])⊆[x]。

因此，xm+1∈Vm∩[x]=[x](m+1)。

于是，当时k→+∞，xk→x*。证毕。

从定理证明中可见，条件一旦满足，运用点迭代(4)代替区间迭代(3)，减少了计算量，提高了计算效率。通过点迭代(4)，不但可以计算绝对值方程(1)的近似解，也可以估算出近似解和准确解之间的差距。

3 对分搜索法

下面，在一个大范围上求解绝对值方程(1)。此时，不必限定绝对值方程(1)有唯一解。对于某个子域，由上面的讨论知，可能有如下情形：

1)若K(y,[x])∩[x]=∅时，方程无解；

2)若wid(K(y,[x])∩[x])≤αwid([x])，其中0≤α<1，那么更新[x]=K(y,[x])∩[x]，在更小的区间上去考虑；

3)若K(y,[x])⊆[x]且wid(K(y,[x]))

下面，我们给出对分搜索的算法。记待对分的子域表为S，不可分子域表为T，不可分长度为h，计算精度为ε，并取正数α，选取Y为非奇异矩阵。

算法如下：

步0 (初始化)清表S和T，把D送入S。

步1 (无解判别)计算式(2)区间函数F([x])，若0∉F([x])，转步8，否则转步2。

步2 (计算)计算K(y,[x])及Z=K(y,[x])∩[x]。

步3 (无解判别)若Z=∅，转步8，否则，转步4。

步4 (存在唯一性判别)计算wid(K(y,[x]))和wid([x])，若K([x])⊆[x]与wid(K([x]))

步5 (点迭代)取x0=mid([x])，由迭代(4)计算{kk}，直到‖xk-xk-1‖≤ε，输出近似解xk，转步8。

步6 (缩小区间)计算wid(Z)，若wid(Z)≤αwid([x])，则令[x]=Z，转步1，否则转步7。

步7 (对分)令[x]=Z，按[x]的最大宽度方向对分[x]，将其一半记入表S的末部，另一半记为[x]。若wid([x])≤h且‖f(mid([x]))‖≤ε，则把[x]记入表T后转步8，否则转步1。

步8 (检查表S)若表S为空，转步9；若S非空，从表末取出最小子域送入[x]，并在表中将取出的部分抹去，转步1。

步9 (检查表T)如表T为空，则输出无解，转步10，否则打印表T的所有子域。

步10 停止。

算法在较大的范围上，通过不断区间迭代和对分的手段，在新的较小区间上考虑绝对值方程(1)解的情况，从而大量删除无解区间。算法的收敛性简单自明。

4 数值算例

我们利用Intlab软件编程，计算下列算例。设计上述算法中的计算精度ε=1e-4，α=0.8。Y=[mid(F′([x]))]-1，若不可能，取Y为单位矩阵。

在[-10,10]上，利用算法求解，得到4个解

利用算法， 在[-10，10]上搜索到下列8个解：

上述算例的数值结果，验证了算法是有效的。

5 结语

区间对分搜索法用于求解绝对值方程(1)，简单易行。算法具有较好的数值稳定性，但随着问题维度的增大，对分的子域数量急剧增多，设计必要的无效区间删除法则是十分有意义的。这是我们接下来要思考的问题。

[1]ROHN J.Systems of linear interval equations[J].Linear Algebra and Its Applications,1989，126(6):39-78.

[2]ROHN J.A theorem of the alternatives for the equation Ax+B|x|=b[J].Linear and Multilinear Algebra,2004,52(6):421-426.

[3]MANGASARIAN O L,Meyer R R.Absolute value equations[J].Linear Algebra and Its Applications,2006,419(5):359-367.

[4]PROKOPYEV O.On equivalent reformulations for absolute value equations[J].Computational Optimization and Applications,2009,44(3):363-372.

[5]ROHN J.On unique solvability of the absolute value equation[J].Optimization Letter,2009,3(4):603-606.

[6]雍龙泉，马守富.绝对值等式问题解的存在性研究[J].新乡学院学报，2010,27(5):19-21.

[7]王爱祥，王海军，龚成.绝对值方程的唯一可解性[J].科学技术与工程，2010,10(34):8501-8502.

[8]MANGASARIAN O L.A generalized Newton method for absolute value equations[J].Optimization Letter,2009(3):101-108.

[9]CACCETTA L,QU B,ZHOU G L.A globally and quadratically convergent method for absolute value equations[J].Computational Optimization and Applications,2011,48(1):45-58.

[10]WANG H J,LIU H,CAO S Y.A verification method for enclosing solutions of absolute value equations[J].Collectanea Mathematica,2013,64(1):17-38.

[11]WANG A X,WANG H J,DENG Y K.Interval algorithm for absolute value equations[J].Central European Journal of Mathematics,2011,9(5):1171-1184.

[12]YONG L Q.Particle swarm optimization for absolute value equations[J].Journal of Computational Information Systems,2010,6(7):2359-2366.

[13]YONG L Q,LIU S Y,ZHANG S M,et al.A new method for absolute value equations based on harmony search algorithm[J].ICIC Express Letters,Part B:Applications,2011,2(6):1231-1236.

[14]雍龙泉.基于差分进化—单纯性混合算法求解绝对值方程[J].计算机应用研究，2011,28(9):3327-3329.

[15]李庆扬，莫孜中，祁力群.非线性方程组的数值解法[M].北京：科学出版社，1987:215-216.

责任编辑：周泽民

Dividing Search Algorithms for Absolute Value Equation with Multiple Solutions

WANG Aixiang

(School of Mechanical and Vehicule Engineering,Changzhou Institute of Technology,Changzhou 213032)

Absolute value equation can be used as a unified framework for study of many optimization problems such as linear programming and quadratic linear programming.Considering that absolute value equations have multiple solutions,an algorithm based on interval mathematics was proposed.Intervals were divided or deleted to obtain each solution of the absolute value equation within a large range.The numerical results verify the validity of the algorithm.

absolute value equation;multiple solution;interval algorithm;Krawczyk operator

10．3969/j．issn．1671⁃0436．2016．06．012

2016-11- 06

王爱祥(1984— )，男，硕士，讲师。

O242

A

1671- 0436(2016)06- 0051- 06