基于Abaqus内填蝴蝶形钢板的自复位钢框架模拟方法探究

黄自尊,李启才

(苏州科技大学，江苏苏州215011 )

基于Abaqus内填蝴蝶形钢板的自复位钢框架模拟方法探究

黄自尊,李启才

(苏州科技大学，江苏苏州215011 )

为了更好地研究自复位结构体系，基于大型通用数值分析软件Abaqus建立了自复位蝴蝶形钢板剪力墙结构的精细有限元模型,详细介绍了自复位结构的建模方法和滞回特性。首先，对经典的角钢耗能的自复位节点试验进行模拟验证，证明了建模方法的可靠性。其次，建立并分析了内填蝴蝶形钢板的自复位钢框架，得到了结构在往复加载下的应力云图、钢绞线应力-层间侧移角曲线和滞回曲线。最后，与理论分析结果对比，检验建模精度。结果表明：单元的选取、接触方程的设置和求解技术的优选是建模成功与否的重要因素；通过Abaqus模拟内填蝴蝶型钢板剪力墙的自复位结构体系与理论符合较好。

自复位框架；有限元模拟；滞回曲线；蝴蝶形钢板剪力墙；Abaqus；角钢

0 引言

传统的钢结构节点利用焊接或者螺栓连接，其变形能力有限，在地震中容易进入塑性甚至发生脆性破坏。1994年美国北岭地震和1995年日本神户地震中，大量的焊接节点发生脆性破坏，其中北岭地震造成的直接损失达150亿美元，这使人们不得不研究新型的抗震节点，自复位节点便是其中之一[1]。

钢板剪力墙作为抗侧力构件的一种，因其经济性和实用性被广泛应用于钢框架体系中。最初出现的非加劲厚钢板墙是利用屈曲前的剪切屈服耗能，后来为了提高材料的利用率，出现了延缓钢板屈曲的加劲钢板墙。随着人们对钢板墙屈曲后性能的认识逐渐成熟，薄钢板墙慢慢出现，但是薄钢板墙在地震中产生的对角拉力带使柱承受额外的剪力，不利于强柱弱梁的抗震设计，而只与柱脱开的薄钢板墙很好地解决了这个问题。以上所述的钢板墙都是利用剪切屈服耗能，但剪切屈服的延性不如弯曲屈服。为了充分发挥材料的延性，目前常用的设计是在墙板中开缝，因此各种几何形式的开缝设计被用于钢板墙中[2]，开蝴蝶形缝的钢板剪力墙便是其中之一。

自复位钢板剪力墙体系是结合了新型自复位节点和钢板剪力墙的高性能抗震结构体系。内填蝴蝶形钢板剪力墙的自复位框架作为该体系的一种构造形式，通过合理的参数设置，可以具备可控的、自复位的性能和可观的延性耗能能力[3]。目前关于自复位蝴蝶形钢板剪力墙结构的研究还处在数值模拟阶段，在该结构的模拟中，不仅要充分考虑材料和几何的双重非线性，还有必要考虑接触非线性。鉴于Abaqus在非线性模拟上的优势，为了更好地研究内填钢板剪力墙的自复位结构体系，有必要对其进行基于Abaqus的模拟研究。

1 横向自复位结构的设计要素和滞回特性

横向自复位结构的设计要素主要包括三部分[3]：一是可摇摆机构，本文的结构采用可自由开合的梁柱节点；二是可替换的耗能器，可以是角钢或者内填钢板墙；三是横向复位元件，本文采用沿梁长横向布置的预应力钢绞线(图1)。在地震中三要素协同工作，既能提供充分耗能所需的节点延性转动能力，又可以将塑性变形控制在可更换耗能器上，还可以保证震后的复位性能，这极大地减少了灾后修复的时间和财力耗费，使中震可修得到了落实。

图1 横向自复位结构

图2 横向自复位结构的理想滞回曲线

理想的横向自复位结构滞回曲线如图2所示，图中各段曲线表示结构所处的各个不同的受力阶段[4]。OA段梁柱节点未打开，相当于线弹性受力阶段的焊接节点。AB段为节点开启后的弹性阶段，此时耗能器未进入塑性耗能。BC段显示随着侧移的加大，节点继续开启，耗能器从部分塑性到完全塑性的阶段。CD段为耗能器完全塑性后，结构完全由弹性阶段的钢绞线提供抗侧力的阶段，这个阶段的结构已经接近极限状态。E点是钢绞线屈服点，应严格控制侧移，避免结构达到E点。只要在E点之前卸载，结构便会继续工作。DH段为结构的复位阶段。DF段为耗能器弹性回复力与钢绞线弹性回复力共同作用的阶段，此时弯矩下降较快。FG段为耗能器逐渐由弹性回复进入反向塑性，但是钢绞线仍然保持弹性回复的阶段。GH段为耗能器完全塑性，钢绞线依然提供弹性回复力的阶段。

在实际的抗震设计中，滞回曲线越饱满，对结构抗震越有利[5]。对于自复位结构而言，复位性能和耗能能力需要相互协调才能达到全面抗震。因此，在结构其他构件始终保持弹性的前提下，可适当放宽复位准则，在图2中直观的表现就是降低H点的位置，甚至允许H点出现在x轴上。

2 建模方法及验证

2.1 自复位节点模拟验证

本文利用有限元软件Abaqus建立了角钢耗能的自复位节点数值模型，为了与潘振华[6]的试件JD2进行对比验证，选取的构造尺寸、材性以及加载方式均与其试验一致，如表1和表2。单根预应力束选取公称直径为15.2mm，抗拉强度为1 860MPa的1×7结构钢绞线。角钢按照材性试验确定的材性，平均屈服强度和抗拉强度分别为437MPa和573MPa。

表1 节点试验梁和柱的主要参数

表2 JD2主要参数

预应力钢绞线沿梁长布置，2行2列共4根，沿梁高方向间距为90 mm，沿梁宽方向间距为150 mm。2个角钢分别外贴于梁柱翼缘，与柱翼缘通过1列2个栓连接，与梁翼缘通过2列4个栓连接。

2.2 模型本构与分析步设置

考虑包辛格效应的影响，梁、柱和角钢的本构均采用三折线随动强化模型。其中，弹性模量E取206 GPa，达到屈服强度后切线模量为0.02E，达到抗拉强度后切线模量降为0。钢绞线的弹性模量取196 GPa，由于严格控制其在弹性范围内受力，在模拟中采用理想弹塑性模型。采用静力通用分析步，开启几何非线性。

2.3 单元选取和网格划分

梁、柱均采用4节点6自由度一次减缩积分壳单元结构化网格划分，沿厚度方向均布5个积分点。考虑到减缩积分的沙漏效应，开启默认沙漏控制；考虑到接触处单元面不能相互渗透和梁腹板的剪切自锁现象，采用线性插值单元。高强螺栓在圆形周边应力集中现象较为明显，因此在该处均采用二次插值三角形单元结构化网格划分。由于不考虑钢绞线的刚度，钢绞线采用2节点3自由度一次桁架单元。结构装配后的有限元模型如图3。

图3 结构有限元模型

2.4 接触和相互作用

对于非线性接触，常用的接触算法有罚函数(Pure Penalty)法和增强拉格朗日(Augmented Lagrange)法，两种方法都是基于罚函数方程。增强的拉格朗日法考虑了额外因子λ，该因子作为额外自由度直接求解，不通过接触刚度与变形计算，优点是可以得到0渗透量，缺点是在0左右函数不连续(跃阶函数)。如果不允许渗透，如图4(a)所示，在Gap为0处，无法判断接触状态是开放或闭合，导致接触震颤，采用迭代求解收敛困难，而采用罚函数法没有此问题(Abaqus 6.14User′s Manual)。因此在本次模拟中，自复位接触的法向接触方式选择硬接触，约束公式采用罚函数公式。切线接触方式选择粗糙，通过摩擦力固定梁的平动自由度。预应力加载通过局部降温法来实现，在施加过程中注意由于变形协调关系导致的预应力损失，需要迭代计算确定最后需降的温度。

(a)拉格朗日法

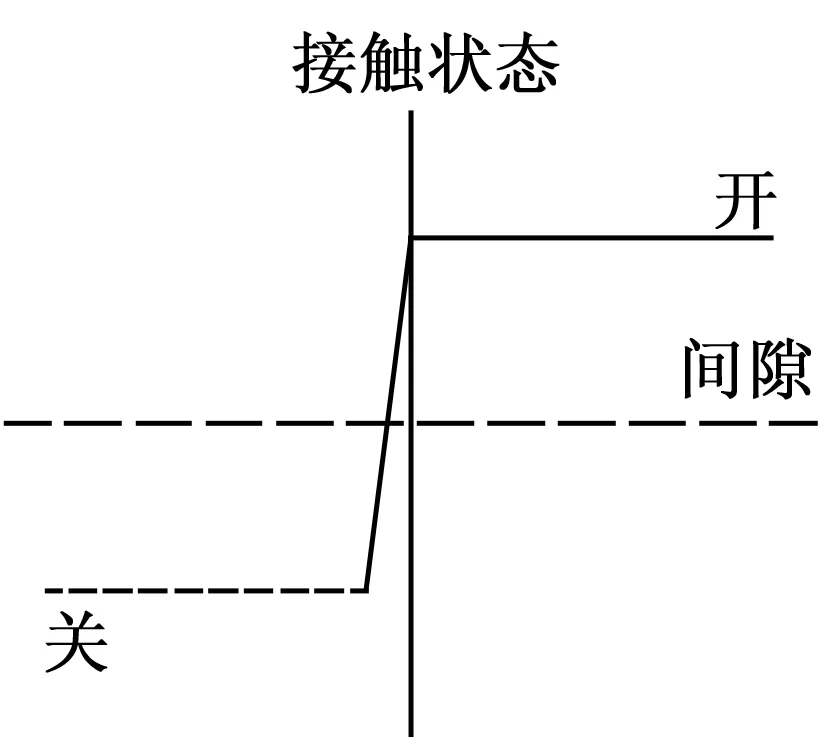
(b)罚函数法

2.5 模拟与试验滞回曲线对比

图5给出了试验和模拟的滞回曲线。从图中可以看出，两条曲线吻合较好，在层间侧移角达到4%时，试验和模拟对应的层间剪力分别为68.5 kN和67.6 kN，两者对应的残余变形分别为0.5%和0.51%，误差均在2%以内，说明用Abaqus软件通过上述建模方法能够可靠地模拟自复位节点。

(a) 试验滞回曲线

(b) 模拟滞回曲线图5 滞回曲线对比

3 内填蝴蝶形钢板剪力墙的自复位钢框架模拟

3.1 分析试件基本信息

本次模拟选取已设计好的单跨钢框架，如图6所示。该自复位钢框架跨度取5 100 mm，层高为3 000 mm。梁和柱的截面尺寸分别为HN350 mm×220 mm×12 mm×16 mm和HW250 mm×250 mm×12 mm×16 mm，材料均取Q345B。梁柱之间采用6根公称直径为15.7 mm的1×7结构钢绞线，其面积为150 mm2，加载90 kN的预应力。

图6 自复位钢框架有限元模型

蝴蝶形钢板墙如图7所示，其中，墙板厚t=4 mm，墙高H=2 650 mm，墙宽W=2 100 mm，板内开缝的长度L=1 000 mm，蝴蝶形短柱的腰宽a=70 mm，蝴蝶短柱的宽度b=182 mm，蝴蝶形短柱的个数n=10，钢材选用Q235B。墙板两侧用尺寸为140 mm×100 mm×3.5 mm的方钢管加劲，钢材选用Q235B。

图7 蝴蝶形钢板墙

装配后的有限元模型如图8所示。为了减小墙剪力对柱产生的影响，墙板只与梁用螺栓连接；通过开蝴蝶形缝使墙板通过蝴蝶形短柱的弯曲耗能，这样既有效限制了墙板面外屈曲，又使结构延性和耗能器工作效率大大提升[7]。

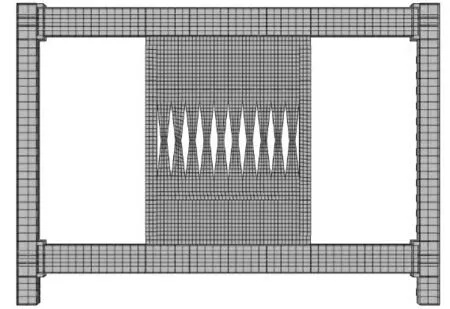
图8 自复位蝴蝶形钢板剪力墙有限元模型

3.2 求解技术与加载制度的选择

本试件的建模方法与前述利用角钢耗能的试件基本一致，试件的加载制度参考美国SAC的标准历程并加以修改[8]。采用位移控制，分7级加载，各级的层间位移角分别是0.375%、0.5%、0.75%、1%、1.5%、2%和3%，每级循环2次。

3.3 应力云图和滞回曲线

模型的应力云图如图9所示，此时的层间侧移角为3%，方向为顺时针。从图中可以看出，框架部分的应力均在Q345B材料的屈服点以下，剪力墙核心部分的应力均超过Q235B材料的屈服点，蝴蝶形短柱均进入塑性耗能，且塑性铰均出现在短柱根部，保证了充分的耗能能力。

图9 自复位蝴蝶形钢板剪力墙应力云图

图10为钢绞线应力-层间侧移角曲线。从图中可以看出，在3%的层间侧移下，不仅钢绞线依然保持弹性，节点也没有出现永久的残余变形。因为一旦节点产生永久变形，会导致钢绞线应力偏离初始应力，在应力位移图中表现为每次循环加载中底端曲线不重合。柱的应力在铰接柱柱脚处和自复位节点处最大，梁的应力分布较均匀，应力最大处都是开合节点周围的梁柱接触区域。

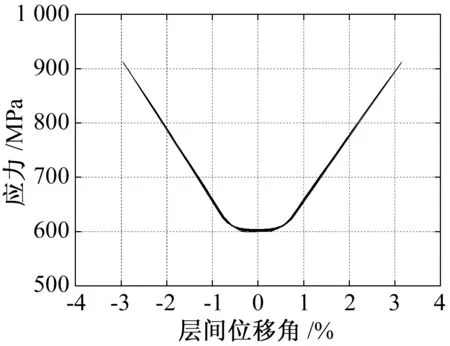
图10 钢绞线应力-层间侧移角曲线

图11为内填蝴蝶形墙板的自复位钢框架模型在静力往复加载下的滞回曲线。相比于自复位结构理想的双旗帜滞回曲线，本模型的滞回环更加饱满。考虑到结构的耗能与滞回环围成的面积成正比，因此该自复位结构具有更优秀的耗能能力，同时，复位性能也可以达到较高的要求。Baldvins等[9]提出控制残余层间位移角限值在0.5%以内，仅需替换耗能器就能实现快速恢复结构使用的功能；我国现行抗震规范[10]规定，多高层钢结构弹塑性层间位移角限值为1/50。在该自复位结构中，当层间侧移角为1/50时，对应的残余层间侧移为0.34%，表明该结构体系在经历严重的地震后，依然可以修复并继续使用。

图11 自复位蝴蝶形钢板剪力墙滞回曲线

4 自复位蝴蝶形钢板剪力墙的理论分析

自复位钢板剪力墙结构的滞回特性可以认为是钢板剪力墙和自复位空框架的叠加[11]，即自复位蝴蝶形钢板剪力墙的初始弹性刚度Ki为蝴蝶形钢板剪力墙弹性刚度KBS和自复位框架初始刚度KPT,i之和。根据文献[3]和文献[11]给出的蝴蝶形钢板剪力墙弹性刚度KBS和自复位框架初始刚度KPT,i可得出Ki的表达式：

Ki=KBS+KPT,i=

式中除了上文提到的参数以外，Hm表示钢板非开孔区域中间壁高度；G表示钢板弹性剪切模量；m表示开孔排数，这里取1；Ib和Ic分别为梁和柱的截面惯性矩。

在节点完全开启且钢板屈服后，该结构的刚度Kd只与自复位框架的刚度有关，根据文献[11]给出的表达式可知：

Kd=KPT,d=

式中：KPT和KHBE分别为钢绞线和梁的轴线刚度；d为节点处梁的高度。

有限元模型主要参数的模拟值和理论值如表3所示，由表3可知，模拟值相对于理论计算值的误差在2%左右，因此利用Abaqus建立的有限元模型与理论分析基本相符。初始刚度Ki模拟值比理论值略小，这是由于理论分析中假定蝴蝶杆在荷载作用下不发生面外变形，理论分析中还假定材料为理想弹塑性，而模拟值采用塑性强化模型，因此剪力墙完全屈服后结构的刚度Kd模拟值略大于其理论值。

表3 主要参数理论值与模拟值对比

5 结论

1)本文详细介绍了采用Abaqus有限元软件建立内填蝴蝶形钢板墙自复位结构精细模型的基本方法，对单元的选取、接触的设置及求解技术的优选进行了详细的分析。

2)本文简要介绍了自复位蝴蝶型钢板剪力墙结构的性能，可概括为：有效减少结构在震后的残余变形，实现复位功能；将永久变形控制在耗能钢板剪力墙上，易于灾后修复；利用蝴蝶形短柱的弯曲耗能，提高结构延性和耗能效率。

3)本文通过模拟验证与理论分析，证明了有限元软件Abaqus能够准确地模拟出自复位蝴蝶形钢板剪力墙的受力特性和滞回性能，可以作为进一步试验研究的参考。

[1]韩建平，王晓燕.新型自复位钢结构体系研究进展[J].结构工程师，2015,8(4):223-224.

[2]郭彦林，周明.钢板剪力墙的分类及性能[J].建筑科学与工程学报，2009,9(3):1-4.

[3]EATHERTON M R,HAJJAR J F.Large-Scale cyclic and hy-brid simulation testing and development of a controlled-rocking steel building system with replaceable fuses[R].NSE-L Report Series,Report No.NSEL-025,Department of Civil and Environmental Engineering,University of Illinois at Urbana-Champaign,2010.

[4]DANIEL M D,RONNY P,MICHEL B.Behavior of self-centering steel plate shear walls and design considerations[J].Journal of Structural Engineering,2012(10):11-14.

[5]顾强.钢结构滞回性能及抗震设计 [M].北京:中国建筑工业出版社，2008.

[6]潘振华.具有自复位能力的钢框架体系研究[D].北京：清华大学,2010.

[7]马磊，李启才.蝴蝶形钢板墙的抗侧刚度和承载力研究[J].苏州科技学院学报，2015(3):30-35.

[8]SAC Joint Venture.Protocol for fabrication,inspection,testing,and docume-ntation of beam-column connection tests and other experimental specimens[EB/OL].[2016-05-10].http://www.docin.com/p-382074943.html?.

[9]BALDVINS N,BERMAN J W,LOWES L N,et al.Dev-elopment of damage prediction models for steel plate shear walls [J].Earthquake Spectra,2012,9(28):2-4.

[10]中华人民共和国住房和城乡建设部，中华人民共和国国家质量监督检验检疫局.建筑抗震设计规范:GB 50011—2010[S].北京:中国建筑工业出版社，2010.

[11]PATRICIA M C.Self-centering steel plate shear walls:Devel-opment of design procedure and evaluation of seismic [D].Washington:University of Washington,2010.

责任编辑：唐海燕

Simulation Test on Self-centering Steel Frame with Infilled Butterfly-Shaped Steel Plate Shear Walls Based on Abaqus

HUANG Zizun,LI Qicai

(Suzhou University of Science and Technology,Suzhou 215011)

In order to study on self-centering steel structural systems properly,a fine finite element modeling method of self-centering steel frame with an infilled butterfly-shaped steel plate shear wall (SPSW) was explored and developed based on the general FEM analysis program Abaqus,with full elaboration on self-centering steel structural system and its hysteretic property.Simulation test was first carried out on self-centering connections with seat angles,which proved the reliability of the modeling method.The FEM of self-centering butterfly-shaped SPSWs was then established and analyzed.Stress nephogram,stress-story drift curves of PT-strands and hysteresis curves of the self-centering butterfly-shaped SPSWs were developed based on the verified modeling method.The simulation results,when compared with the theoretical analysis,show that selection of element type,constraint enforcement method and optimization of solution are the crucial factors for the FEM analysis.Self-centering butterfly-shaped SPSWs can be simulated accurately by Abaqus.

self-centering steel frame；finite element simulation；hysteresis；butterfly-shaped infill wall;Abaqus;angle

10．3969/j．issn．1671⁃0436．2016．06．002

2016- 07- 01

国家自然科学基金项目(51378326)；江苏省结构工程重点实验室基金项目(ZD1204)

黄自尊(1991— )，男，硕士研究生。

TU398+.2

A

1671- 0436(2016)06- 0006- 06