基于改进非参数核密度估计和拉丁超立方抽样的电动公共客车负荷模型
缪鹏彬余 娟史乐峰刘国平梁 明李文沅任洲洋(. 输配电装备及系统安全与新技术国家重点实验室(重庆大学) 重庆 400044 . 国网重庆市电力公司电力科学研究院 重庆 403)
基于改进非参数核密度估计和拉丁超立方抽样的电动公共客车负荷模型
缪鹏彬1余 娟1史乐峰2刘国平2梁 明1李文沅1任洲洋1
(1. 输配电装备及系统安全与新技术国家重点实验室(重庆大学) 重庆 400044 2. 国网重庆市电力公司电力科学研究院 重庆 401123)
摘要为了建立更精确的电动公共客车充电负荷模型,对起始荷电状态和起始充电时间的概率分布和抽样方法进行研究。首先针对概率分布,提出采用边界核的自适应非参数核密度估计算法,该方法无需概率分布的任何假设,能有效解决边界偏差和缺乏局部适应性的问题,从而提高了起始荷电状态和起始充电时间概率分布的准确度和适应性。其次针对抽样环节,提出结合三次样条插值法的改进拉丁超立方抽样算法,该方法不仅可以解决累积分布函数的反函数较难求解的问题,而且具有准确度高、抽样规模小等优点。最后,以这两种算法为基础,建立电动公共客车充电负荷模型,并将其与实测数据和传统参数估计方法所得结果进行对比。仿真结果证明了所提方法的适应性和有效性。
关键词:电动公共客车 充电负荷 自适应非参数核密度估计算法 边界核 拉丁超立方抽样
国家自然科学基金(51477017),重庆市基础与前沿研究计划一般项目(cstc2014jcyjA90017)和国家电网公司科技项目(SGCQDK00DJJS1500056)资助。
Electric Public Bus Load Model Based on Improved Kernel Density Estimation and Latin Hypercube Sampling
Miao Pengbin1Yu Juan1Shi Lefeng2Liu Guoping2Liang Ming1Li Wenyuan1Ren Zhouyang1(1. State Key Laboratory of Power Transmission Equipment & System Security and New Technology
Chongqing University Chongqing 400044 China
2. Chongqing Electric Power Research Institute Chongqing 401123 China)
Abstract To build a more precise charging load model of electric public buses, the probability distribution and sampling method of charging state and charging start time are studied. Firstly, an adaptive kernel density estimation with boundary Kernel algorithm is proposed to build probability distribution models. The proposed algorithm does not require any assumptions about the probability distribution, and can also solve the problems of boundary bias and lacking of local adaptability, which improves the precision and adaptability of probability distribution. Secondly, Latin hypercube sampling with cubic spline interpolation algorithm is proposed to figure out the inverse cumulative distribution function of probability distribution. The proposed algorithm has high precision and sampling efficiency. Finally, based on these two algorithms, electric public bus charging load model is set up. The simulation result demonstrates the effectiveness and adaptability of the proposed method.
Keywords:Electric public bus, charging load, adaptive Kernel density estimation, boundary Kernel, Latin hypercube sampling
0 引言
电动汽车作为新一代的交通工具,具有低能耗、低污染的巨大优势,在可以预见的未来将迎来飞速的发展。对电动汽车的充电负荷进行建模是研究电动汽车对电网影响、充电基础设施规划以及电网规划与运行的前提[1,2]。电动汽车目前主要分为私家车、公共客车和出租车三类,其中电动公共客车的发展较为快速。电动公共客车一般集中在大型充电站进行快速充电,配套有较为完善的充电数据采集系统,能够为基于概率统计方法建立其充电负荷模型提供充足的历史数据。
目前电动汽车充电负荷模型研究广泛采用基于蒙特卡洛模拟的统计学建模方法[3-6]。该方法是在建立诸如起始荷电状态(State Of Charge, SOC)、起始充电时间等概率分布的基础上,考虑充电功率、电动汽车数量及电池容量等影响因素,运用蒙特卡洛数学试验累加每辆电动汽车的充电负荷得到总体充电负荷。考虑到电动公共客车一般集中在大型充电站进行快速充电(充电功率恒定,充至满电),且具有电池容量标配,日充电次数基本恒定等特点,因此起始SOC和起始充电时间的精确概率分布是决定电动公共客车充电负荷模型的关键因素。
目前一般采用传统参数估计方法建立起始SOC和起始充电时间的概率分布,即预先假设其概率密度函数服从某种分布,然后依据历史样本数据来估计该分布的参数。对于起始SOC,大部分文献假设其服从正态分布[3,7],文献[5]则假设其服从广义极值分布;对于起始充电时间,大部分文献假设其服从均匀分布[6,8],文献[3]则根据不同车辆类型,假定其服从均匀分布、正态分布和直角梯形分布,文献[5]假定其服从威布尔分布。这些概率分布模型虽有不同,但是均属于传统参数估计范畴。如果假设的概率分布与实际情况不符,那么必然会导致计算所得的充电负荷模型偏差较大。因此,引入非参数核密度估计(Kernel Density Estimation, KDE)算法是十分必要的,该算法不需要概率分布的任何假设,能够揭示隐藏在历史样本数据中的统计信息,有效提高概率分布准确度。需要指出的是,本文所分析的起始SOC和起始充电时间都是有上、下界约束的数据,利用KDE算法求解其概率分布时会在上、下边界处出现边界偏差(随机变量上、下边界以外的概率密度值仍然大于0,从而造成误差),这可以通过采用边界核的KDE算法来解决[9];此外,数据分布的光滑程度不具有一致性,KDE算法假设样本区间内光滑程度一致(采用固定带宽)较为理想化,与实际情形不符,对此B. W. Silverman提出了自适应核密度估计法[10],从而解决了KDE算法存在的缺乏局部适应性问题。相较传统参数估计方法,采用自适应核密度估计法对于不同充电场景下的充电负荷特性具有更好的适应性。本文将边界核与自适应核密度估计法相结合,提出基于边界核的自适应非参数核密度估计(Adaptive Kernel Density Estimation with Boundary,AKDEB)算法,以有效解决KDE算法存在的边界偏差和缺乏局部适应性的问题。
基于非参数核密度估计算法的概率密度函数是求和形式,其累积分布的反函数难以求解。因此,在非参数核密度估计抽样中,不依赖于累积分布反函数的舍选法得到了一定的应用[11],而相比舍选法抽样规模更小、准确度更高的拉丁超立方抽样(Latin Hypercube Sampling,LHS)方法则无法直接应用[12]。然而,基于一组已知的样本值和对应的累积概率,利用插值法便可以求解出任意累积概率所对应的样本值,三次样条插值法由于计算简便、光滑性好和准确度高等优点得到了广泛应用[13]。因此,本文提出一种基于三次样条插值法的改进拉丁超立方抽样(LHS with Cubic Spline Interpolation,LHS-CSI)法,以解决累积分布反函数难以求解时不能应用LHS方法的问题,并且保留了LHS方法抽样规模小、准确度高的优点。
综上,本文首先提出AKDEB算法建立起始SOC和起始充电时间的概率分布模型;其次,提出LHS-CSI算法对起始SOC和起始充电时间进行抽样,并建立电动公共客车充电负荷模型;最后,以重庆市渝北空港电动客车专用充电站的实际统计数据为基础进行仿真分析,以验证本文所提方法的适应性和有效性。
1 基于AKDEB估计算法的起始SOC和起始充电时间概率分布
本文所提的AKDEB算法结合了边界核和自适应核密度估计的优点,可以很好地解决KDE算法存在的边界偏差和缺乏局部适应性的问题。
下面介绍该算法的具体原理:假设X1, X2,…, Xn为n个样本,定义域为[a,b],概率密度函数为f(x),则此概率密度函数的KDE估计[8]为
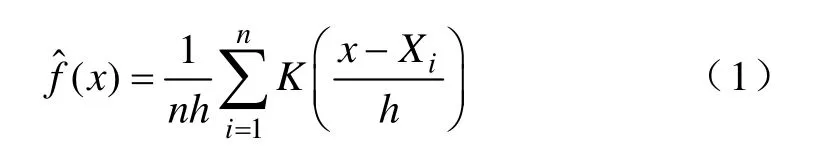
常规KDE算法存在边界偏差问题,可以通过使用“边界核”这一特殊的核函数来修正[9]。边界核的表达式为

式中
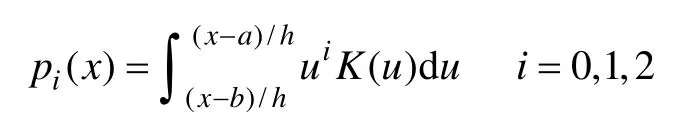
将式(1)中的K(Z)用式(2)表示的边界核B(Z)进行替换,即得到采用边界核的核密度估计为

采用式(3)的核密度估计仅仅能解决边界偏差,但是由于采用的是固定带宽h,因此并不能根据局部区域的样本数据调节带宽,从而存在缺乏局部适应性的问题,对此B. W. Silverman提出了自适应核密度估计法[10],即把式(1)中的h用式(4)代替。式中,f
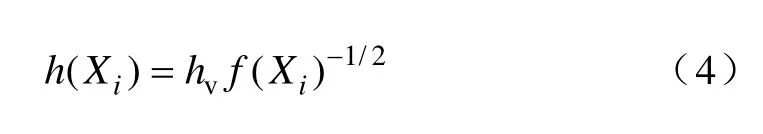
(Xi)一般采用式(1)的估计值作为先导估计。hv则是由交叉验证法[10]得到的最优带宽。
本文将边界核与自适应核密度估计算法相结合,提出AKDEB算法,即把式(3)中的固定带宽h用式(4)的可变带宽h(Xi)代替,则概率密度函数的AKDEB估计为
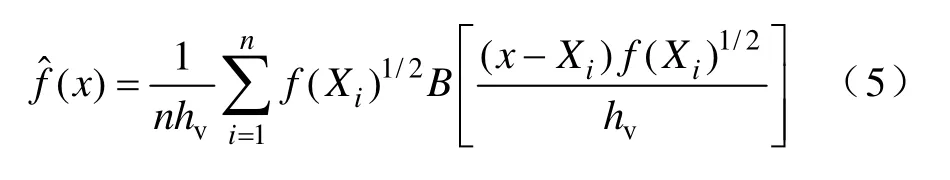
需要注意的是,由于式(5)中的边界核结合了自适应核密度估计算法, 因此原来的相应地转变为。
以起始SOC和起始充电时间的历史样本数据为基础,利用式(5)便可以得到其概率密度估计。起始SOC和起始充电时间在边界以外的概率密度估计值为0,在边界以内则会根据局部区域的样本数据调节带宽,这样就可以解决常规KDE算法的边界偏差和缺乏局部适应性问题。
2 基于LHS-CSI抽样算法的电动公共客车充电负荷模型
首先对本文提出的LHS-CSI算法的基本原理进行介绍;然后,基于LHS-CSI抽样算法对起始SOC和起始充电时间进行随机抽样,建立电动公共客车充电负荷模型。
2.1 LHS-CSI抽样算法
对于某一随机变量X,定义域为[a,b],累积概率分布函数为

设N代表采样规模,采用中值拉丁超立方抽样法将曲线Y=F(X)的纵轴分成N个等间距不重叠的区间,选择每个区间的中点作为Y的采样值yk=(k-0.5)/N (k=1,2,…,N),然后用函数Y=F(X)的反函数来计算随机变量X的第k个采样值为

以上介绍的是常规LHS的采样方法,但是本文中F-1(yk)的显式表达式难以求解,因此需要借助三次样条插值法[14]:
(1)将随机变量X的定义域[a,b]均分为m个点(a=x1<x2<…<xm-1<xm=b),并根据式(5)求出点xi(i=1,2,…,m)处的概率密度估计值,从而点xi处的概率估计值近似等于因此点xi处的累加概率估计值为

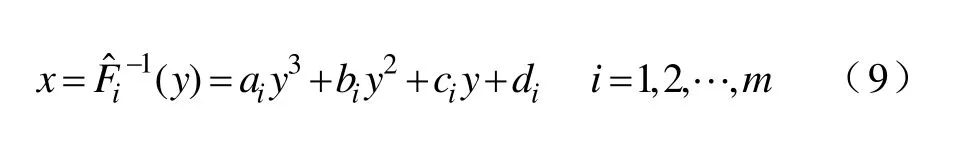
(3)对于任一累积概率值yk=(k-0.5)/N,k= 1,2,…,N,一定落在某个小区间内,将yk代入式(9)则可以求解出样本值。
经过以上步骤,便可以得到N个起始SOC和起始充电时间的随机样本,为建立电动公共客车充电负荷模型提供数据输入。LHS-CSI算法准确度高、抽样效率高的特点可以保证最后建立电动公共客车充电负荷模型的准确性和高效性。
2.2 电动公共客车充电负荷模型
假设充电站一天内接纳M车次(同一辆电动公共客车一天内可能充电多次,M车次表示充电站一天内所有电动公共客车的充电总次数)的待充车辆,所有待充电动公共客车的电池容量为Cap,充电过程近似为恒功率充电,充电功率为Pc。对于任意第i (i=1,2,…,M)车次的待充公共客车,由2.1节可以得到它对应的起始SOC和起始充电时间样本值,记作(Si,ti)。根据Si可以直接计算出其充电持续时间为
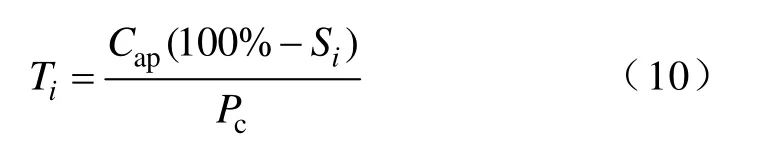
根据式(10)得到的充电持续时间Ti,可以得出该车辆的充电时间区间为[ti, ti+Ti]。定义电动公共客车的上班时间为tstart,下班时间为tend,则上班时间内任一时刻t的充电负荷可以表示为

式中
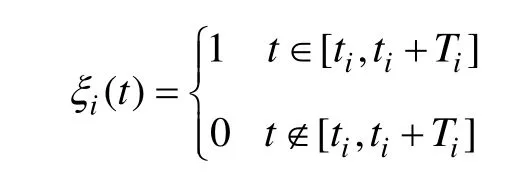
利用式(11)可以求解出任意时刻t的充电负荷,当求解出区间[tstart, tend]内所有时刻点的充电负荷并连接成线时,即可求出最终的充电日负荷曲线。实际应用中,一般以Δt(Δt可以取为1s、1min和1h等)为时间间隔将区间[tstart, tend]分为若干个小区间,求解出小区间上的充电负荷并连接成线,形成最终的日负荷曲线,具体计算流程如图1所示。
3 算例分析
3.1 数据描述
本文采用重庆市渝北空港电动客车专用充电站的实际统计数据(2013年3月~2014年4月)来证明所提方法。该充电站电动公共客车采用Pc=260kW恒功率充电。电池容量Cap=100kW·h。上班时间tstart=420min(上午7点),下班时间tend=1 290min(晚上9点半)。起始SOC的定义域为[0,100],m=101(起始SOC概率密度直方图的区间间隔为1%)。起始充电时间的定义域为[420min,1 290min],m=871(起始充电时间概率密度直方图的区间间隔为1min)。充电站日接纳车次M=100。采样规模N=10 000。充电负荷曲线计算时间步长为Δt =1min。Matlab运行的计算机环境为Inter Core 2 Duo核处理器,内存8G。

图1 电动公共客车充电负荷计算流程Fig.1 Flowchart of the electric public bus charging load
3.2 起始SOC和起始充电时间概率分布的仿真结果分析
本文采用卡方检验和后验检验[15]作为评估概率分布拟合优度的指标。表1和表2给出了起始SOC和起始充电时间的常用概率分布的卡方检验结果。卡方统计量越小表明概率分布的拟合效果越好。从表中可以看出,在几种常用的传统参数估计方法中,正态分布对于起始SOC的拟合相对较好,均匀分布对于起始充电时间的拟合误差也在可接受的范围内,因此这两种分布模型的广泛使用具有一定的合理性。然而,采用传统参数分布时其估计结果均不能通过严格统计意义的卡方检验;相比之下,采用非参数核密度估计方法的卡方统计量均远小于传统参数估计方法的统计量,而且能通过卡方检验。本文提出的AKDEB算法比KDE算法的卡方统计量更小,其拟合效果更优。

表1 起始SOC四种概率分布的卡方检验结果Tab.1 Chi square test results of four probability distribution models with SOC
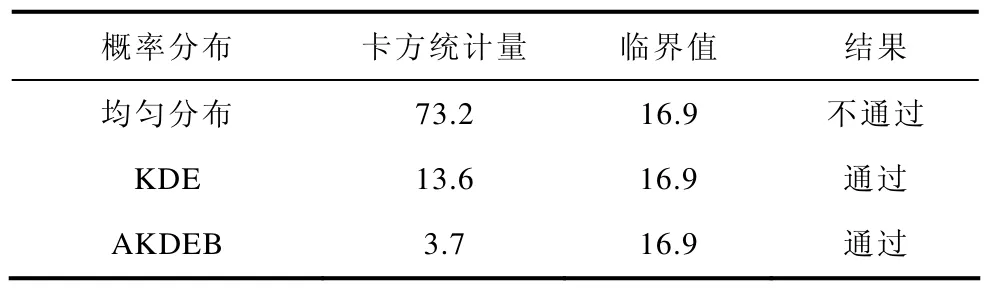
表2 起始充电时间三种概率分布的卡方检验结果Tab.2 Chi square test results of three probabilitydistribution models with charging start time
图2和图3分别给出了起始SOC和起始充电时间的概率密度曲线和直方图。从图2和图3的后验检验也可以看出本文所提的概率分布较之传统参数分布具有更好的拟合准确度。综上,本文提出的AKDEB算法可以有效提高概率分布模型的准确度。
由图2和图3还可以得出以下两个结论:
(1)常规KDE算法形成的概率密度曲线确实存在边界偏差,起始SOC<0和SOC>100%处的概率密度值仍然是>0的,起始充电时间在<420min和>1 290min处的概率密度值也是>0的,而这些都是与实际情况不相符的,相比之下,本文所提出的AKDEB算法修正了边界偏差,符合实际情况,进一步提高了拟合准确度。
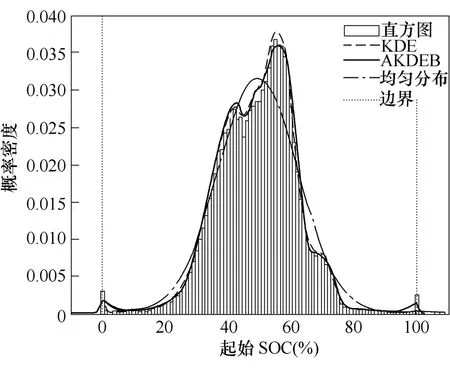
图2 起始SOC概率密度曲线和直方图Fig.2 The probability density curve and histogram of SOC

图3 起始充电时间概率密度曲线和直方图Fig.3 The probability density curve and histogram of charging start time
(2)从图3可以看出AKDEB算法所得的概率密度曲线中部较为粗糙,即曲线中部的带宽值较小,而曲线两端则较为光滑,即曲线两端的带宽值较大,从而实现了带宽值根据样本数据的变化进行调节,解决了KDE算法缺乏局部适应性的问题。
3.3 起始SOC和起始充电时间抽样的仿真结果分析
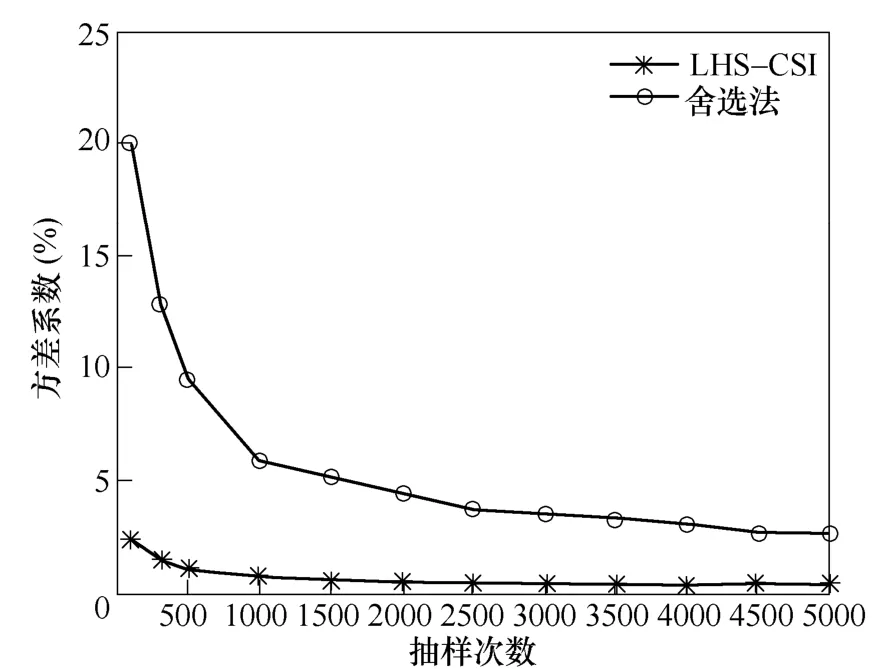
图4 LHS-CSI算法和舍选法准确度对比Fig.4 Accuracy comparison between LHS-CSI and acceptance-rejection sampling algorithm
本文以起始SOC为例,采用方差系数作为衡量LHS-CSI算法和舍选法准确度的指标。图4、图5给出了本文抽样方法和舍选法在准确度和抽样时间上的对比。在抽样准确度方面,如图4所示,如果以方差系数1%作为收敛判据,那么LHS-CSI算法在抽样次数为500次左右时即可收敛,而舍选法在抽样次数达到5 000次时仍未收敛,经过进一步计算,抽样次数达到20 000次时舍选法才能收敛。如果以方差系数5%作为收敛判据,那么LHS-CSI算法在抽样次数为20次时即可收敛,而舍选法在抽样次数达到1 500次时才能收敛。在抽样时间方面,如图5所示,由于LHS-CSI算法的抽样时间主要集中在计算典型点xi(a=x1<x2<…<xm-1<xm=b)处的概率密度估计值,因此在m选定的情况下抽样时间基本保持不变。但是,舍选法每次抽样都需要进行概率密度值的计算,因此其计算时间会随着抽样次数的增加呈线性增长的趋势。综上,LHS-CSI算法在准确度和抽样时间上均优于舍选法。
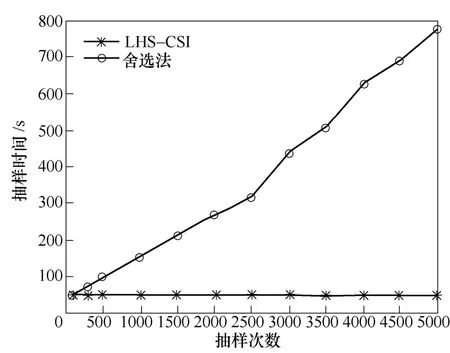
图5 LHS-CSI算法和舍选法抽样时间对比Fig.5 Time comparison between LHS-CSI and acceptance-rejection sampling algorithm
3.4 电动公共客车充电日负荷曲线的仿真结果分析
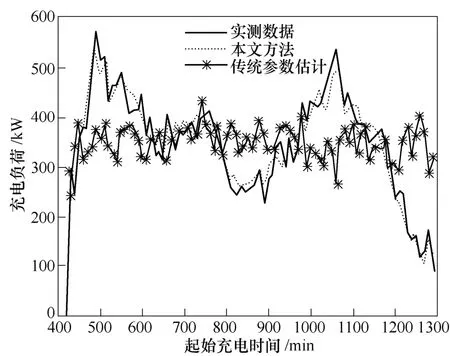
图6 基于AKDEB算法与传统参数估计算法的电动公共客车充电日负荷曲线Fig.6 Daily load curves of the electric public buses based on AKDEB and traditional parameter estimation algorithm
图6给出了三条充电日负荷曲线,依次对应于实测数据、本文所提方法、传统参数估计方法,其中,传统参数估计方法中对起始SOC和起始充电时间分别采用的是正态分布和均匀分布。从三条日负荷曲线的对比可以看出,采用本文方法对电动汽车充电负荷进行建模时与实际情况较为接近,其曲线走势基本与实测数据相同,而传统参数统计方法仿真结果与实测数据之间的误差较大,其误差最大的两个区域集中在上午9∶20和晚上8∶40左右。
表3给出了以平均相对误差、峰(谷)时相对误差为指标的两种方法的准确度对比。从表中可以看出,采用传统参数估计方法所得的充电日负荷曲线与实测数据的误差均远大于本文所提算法的误差,传统参数估计方法的谷时相对误差更是达到了208.9%。综上,本文所提方法可以有效提高电动公共客车充电负荷模型的准确度。
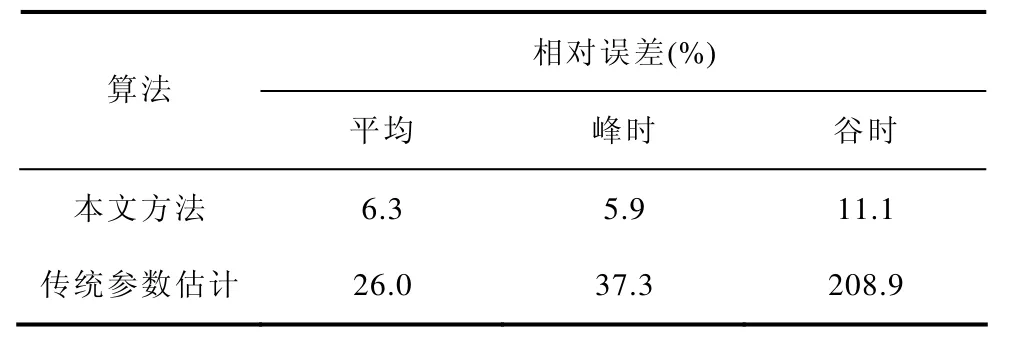
表3 本文方法和传统参数估计方法的准确度对比Tab.3 Accuracy comparison between AKDEB and traditional parameter estimation algorithm
4 结论
首先,本文提出了AKDEB估计算法,并利用该算法对起始SOC和起始充电时间的概率分布进行了研究。该算法不需要概率分布的任何假设,能够揭示隐藏在历史样本数据中的统计信息,有效提高了概率分布的准确度。此外,该算法将边界核和自适应核密度估计方法的优点有效结合,解决了常规KDE算法存在的边界偏差和缺乏局部适应性的问题。其次,本文提出了LHS-CSI抽样算法,对起始SOC和起始充电时间进行随机抽样。该算法解决了累积分布函数的反函数难以求解显示表达式时不能直接应用LHS抽样方法的问题,且有效保留了LHS方法抽样准确度高、计算时间短的优点。最后,基于本文所提的以上两种算法,建立了电动公共客车充电负荷模型。本文所提出方法准确度高、适应性强且效率高,保证了最终所得到的充电负荷模型的准确性、适应性和高效性,为研究电动汽车对电网影响、充电基础设施规划以及电网规划与运行等问题打下了良好的基础。仿真结果证明了本文所提方法的适应性和有效性。
参考文献
[1] 葛文捷, 黄梅, 张维戈. 电动汽车充电站经济运行分析[J]. 电工技术学报, 2013, 28(2): 15-21.
Ge Wenjie, Huang Mei, Zhang Weige. Economicoperation analysis of the electric vehicle charging station[J]. Transactions of China Electrotechnical Society, 2013, 28(2): 15-21.
[2] 肖湘宁, 温剑锋, 陶顺,等. 电动汽车充电基础设施规划中若干关键问题的研究与建议[J]. 电工技术学报, 2014, 29(8): 1-10.
Xiao Xiangning, Wen Jianfeng, Tao Shun, et al. Study and recommendations of the key issues in planning of electric vehicles’ charging facilities[J]. Transactions of China Electrotechnical Society, 2014, 29(8): 1-10.
[3] 罗卓伟, 胡泽春, 宋永华, 等. 电动汽车充电负荷计算方法[J]. 电力系统自动化, 2011, 35(14): 36-42.
Luo Zhuowei, Hu Zechun, Song Yonghua,et al. Study on plug-in electric vehicles charging load calculating[J]. Automation of Electric Power Systems, 2011, 35(14): 36-42.
[4] 杨冰, 王丽芳, 廖承林. 大规模电动汽车充电需求及影响因素[J]. 电工技术学报, 2013, 28(2): 22-27.
Yang Bing, Wang Lifang, Liao Chenglin. Research on power-charging demand of large-scale electric vehicles and its impacting factors[J]. Transactions of China Electrotechnical Society, 2013, 28(2): 22-27. [5] Pashajavid E, Golkar M A. Charging of plug-in electric vehicles: Stochastic modelling of load demand within domestic grids[C]//2012 20th Iranian Conference on Electrical Engineering, 2012: 535-539.
[6] 徐国钧, 刘永胜, 李题印, 等. 基于层次分析和概率模拟的电动汽车对配网负荷影响研究[J]. 电力系统保护与控制, 2012, 40(22): 38-45.
Xu Guojun, Liu Yongsheng, Li Tiyin, et al. Study on the impact of electric vehicles charging load integrated into distribution network based on analytic hierarchy process and probabilistic simulation[J]. Power System Protection and Control, 2012, 40(22): 38-45.
[7] Leou Rong Ceng, Su Chun Lien, Lu Chan Nan. Stochastic analyses of electric vehicle charging impacts on distribution network[J]. IEEE Transactions on Power Systems, 2014, 29(3): 1055-1063.
[8] Dai Qian, Cai Tao, Duan Shanxu, et al. Stochastic modeling and forecasting of load demand for electric bus battery-swap station[J]. IEEE Transactions on Power Delivery, 2014, 29(4): 1909-1917.
[9] Jeffery S Simonoff. Smoothing methods in statistics[M]. New York: Springer-Verlag, 1996.
[10] Silverman B W. Density estimation for statistics and data analysis[M]. Boca Raton: CRC Press, 1986.
[11] 赵渊, 张夏菲, 周家启. 电网可靠性评估的非参数多变量核密度估计负荷模型研究[J]. 中国电机工程学报, 2009, 29(31): 27-33.
Zhao Yuan, Zhang Xiafei, Zhou Jiaqi. Load modeling utilizing nonparametric and multivariate Kernel density estimation in bulk power system reliability evaluation[J]. Proceedings of the CSEE, 2009, 29(31): 27-33.
[12] Mckay M D, Beckman R J, Conover W J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code[J]. Technimetrics, 1979, 21(2): 239-245.
[13] Young T, Mohlenkamp M J. Introduction to numerical methods and Matlab programming for engineers[M]. Athens: Ohio University, 2012.
[14] 张德丰, 等. MATALAB 数值计算方法[M]. 北京:机械工业出版社, 2010.
[15] Qin Zhilong, Li Wenyuan, Xiong Xiaofu. Estimating wind speed probability distribution using Kernel density method[J]. Electric Power Systems Research, 2011, 81(12): 2139-2146.
缪鹏彬 男,1991年生,硕士研究生,研究方向为电动汽车与电网安全稳定分析。
E-mail: miaopengbin@qq.com
余 娟 女,1980年生,博士,副教授,研究方向为无功优化、风险评估、电压稳定与电力系统静态等值。
E-mail: cqu.juan.yu@gmail.com(通信作者)
作者简介
收稿日期2014-09-23 改稿日期 2015-09-17
中图分类号:TM743; U469.72+1

