基于单端电气量的不对称参数同塔四回线选相方法

刘 琦邰能灵范春菊于仲安尚（. 上海交通大学电子信息与电气工程学院 上海 0040 . 江西理工大学电气工程与自动化学院 赣州 34000）



基于单端电气量的不对称参数同塔四回线选相方法

刘 琦1邰能灵1范春菊1于仲安2尚1
（1. 上海交通大学电子信息与电气工程学院 上海 200240 2. 江西理工大学电气工程与自动化学院 赣州 341000）

摘要不对称参数的同塔四回线具有不同的自感参数，无法使用传统的12序分量法进行解耦，因此采用相线解耦法对其进行解耦，并将相电流分解为12个独立的序电流分量，解决了同塔四回线中的互感耦合问题。线路发生故障时，利用故障边界条件得到序分量之间的关系。在不同回线上发生故障时，穿越序分量与环流序分量的序电流相位分别呈现出同相或反相的特征；同一回线发生不同类型故障时，序分量电流之间满足固定的幅值关系；同一类型的不同相序故障时，序分量相位差满足特定关系。考虑故障点分布系数对保护测量装置的影响，提出适于不对称参数同塔四回线发生单回线故障时的故障识别方法，并构造了相应的选相判据，给出了选相流程和方法。PSCAD/EMTDC仿真结果表明，此选相方法具有良好的选择性，不受故障类型，故障点的位置以及过渡电阻的影响。

关键词：不对称参数 同塔四回线 选线 选相 序分量 单端电气量

国家自然科学基金资助项目（51177066、51377104）。

Fault Phase Selection Scheme for Quadruple-Circuit Transmission Lines with Asymmetrical Parameter Based on Single-Ended Electrical Quantities

Liu Qi1Tai Nengling1Fan Chunju1Yu Zhongan2Shang Jin1
（1. School of Electronic Information and Electrical Engineering Shanghai Jiaotong University Shanghai 200240 China 2. School of Electrical Engineering and Automation Jiangxi University of Science and Technology Ganzhou 341000 China）

Abstract The asymmetrical quadruple-circuit lines have different self-inductances, which cannot be decoupled by the twelve-sequence-component method. Phase-Line decouple method is adopted to eliminate the mutual inductance, and convert the original phase currents into 12 different independent current components. When a line fault occurs, the boundary conditions help to find out the relationship between the current components. If a fault occurs on different lines, the across components and loop components are in the same or inverse phase. The amplitudes of the components are the same while the phases are shifted a special angle during the same kind of fault on the different phase of same line. Considering the influence of the distributed factors, a fault phase selection method for asymmetrical quadruple-circuit lines is presented, flow chart for fault phase is also provided. The PSCAD/EMTDC simulation results show that this method is suitable for fault phase selection, and the fault location and fault resistance has little influence on this method.

Keywords：Asymmetrical parameter, quadruple line on the same tower, line selection, phase selection, sequence component, single terminal electric quantities

0 引言

随着我国的经济发展与改革深化，土地资源日益紧张，土地占用成本在输电线路总成本的比例越来越高。为了节省用地，经济建设输电线路，国内已大量采用了双回输电线路，而采用同塔四回线输电不仅能更有效地解决输电走廊面临的土地资源问题，而且能显著提升输电容量[1]。同塔四回线在节省土地并提高供电可靠性的同时，也给继电保护相关技术带来很大的挑战。

国内外对于同塔双回线和同塔四回线的研究已有大量的文献报道[2-7]，对于多回线的故障分析，通过矩阵变换消去互感对故障分析的影响得到了广泛的认同。文献[8, 9]通过矩阵变换对四回线的互感进行解耦，得到了适于四回线解耦的12序分量法。文献[10]对12序分量法进行改进，提出了12序分量扩展法。这两种方法为同塔四回线的故障计算、故障测距和故障选线等方向奠定了坚实的基础。文献[11]基于12序分量法，提出了适于同塔四回线的故障选线方法。文献[12,13]利用12序分量法得到的环流量，实现了故障选线和故障选相。文献[14,15]利用序分量构建了同塔多回线的故障测距方法。文献[16]研究了非同程同塔四回线的故障选线。

不对称参数同塔四回线无法采用上述两种解耦分析方法。不对称参数同塔四回线中的杆塔结构在空间上具有一定的左右对称性。对于六层塔的四回线路，顶层两回线的回线内自感与互感相同，底层两回线的回线内自感与互感相同，但顶层两回线与底层两回线的自感与互感不相同。采用上述两种解耦分析方法解耦，零序分量将无法被完全解耦，不能得到相互独立的序分量，之后的故障分析会出现错误。文献[17,18]为同塔四回线的解耦提供了新方法，但仍无法解决不对称参数同塔四回线的解耦问题。本文采用相线解耦法对其解耦，并将相电流分解为12个独立的序电流分量，解决了同塔四回线中的互感耦合问题。

通过对不对称参数四回线发生各种故障时，各个序分量所表现出的特征进行大量研究，本文发现两个特点：①线路发生单回线故障的情况下，在不同回线上发生故障时，序分量电流之间存在固定的相位关系；②同一回线发生不同类型故障时，序分量电流之间存在固定的幅值和相位关系。结合上述两点，本文提出一种四回线路发生单回线故障时的完整选线、选相方法。这种方法消除了四回线互感的影响，能够准确地对四回线故障进行故障选线和选相。

1 不同参数四回线的解耦方法

在不对称同塔四回线中，每回线的自阻抗和互阻抗与其他回线的自阻抗和互阻抗不完全对应一致。当使用传统解耦方法，如12序分量法，对阻抗矩阵解耦时，将无法完全解耦。文献[10]对12序分量扩展法进行了进一步推广，推导了适于不对称四回线的特征值和特征向量。本文在此基础上，利用特征值与特征向量的关系，最终构建出如式（1）所示的解耦矩阵M，实现不对称同塔四回线的阻抗解耦。

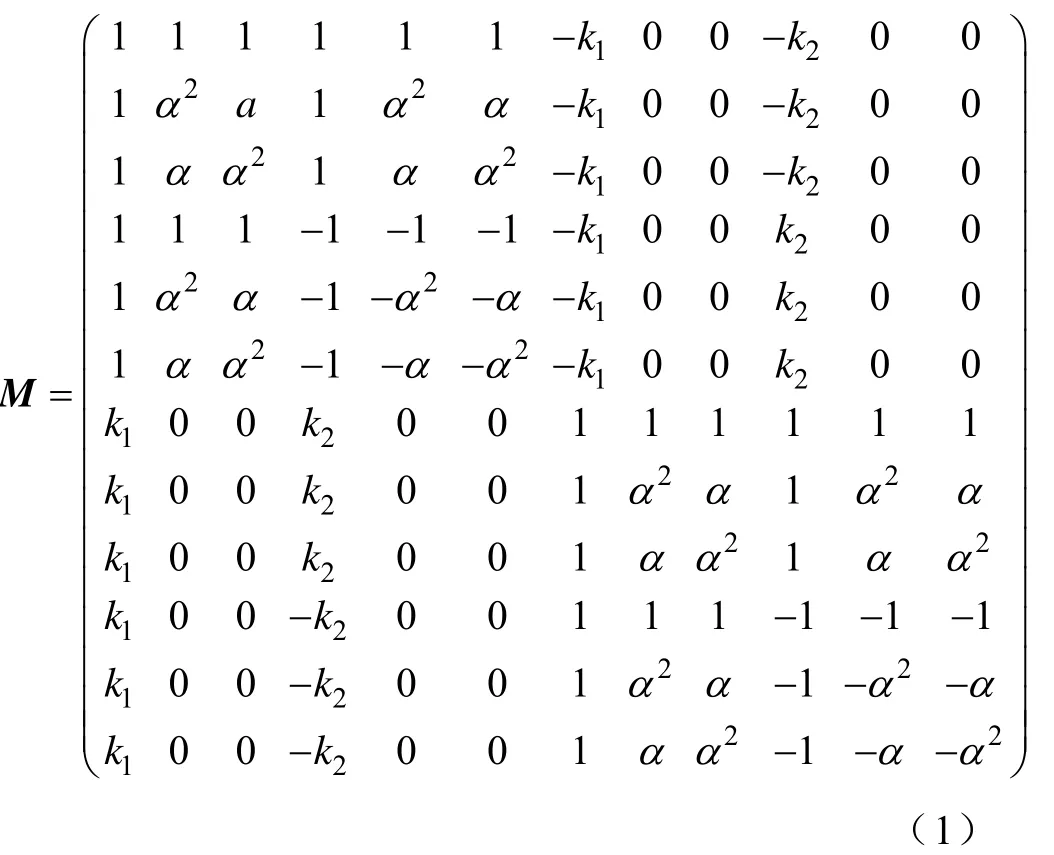
式中，k1、k2为不对称补偿系数，主要用于补偿线路自感与互感的不对称，其计算式为

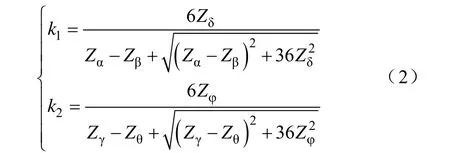
式中

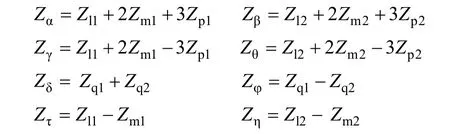
经相线解耦法对矩阵解耦后，可得到12个独立的序电流。正序分量包含e1、f1、g1和h1；负序分量包含e2、f2、g2和h2；零序分量包含e0、f0、g0和h0。其中，e序分量和g序分量在四回线内、外均存在，称为穿越序分量；而f序分量和h序分量仅在四回线内部存在，称为环流序分量。

由相线解耦法可得到电流序分量与各相电流之间的关系为

由式（2）可看出，不对称补偿系数k1和k2是关于线路自身参数的表达式，因此当线路参数固定时，不对称补偿系数也随之确定。在进行计算时，不对称系数可视为一个常数，结合式（3）可知，序分量电流是相电流的常系数的线性组合，与系统运行状态无关。

2 故障选线原理及方法

输电线路发生故障时，各相序电流在不同的故障类型时呈现不同的特征。由于序电流分量为相电流的线性组合，因此序电流分量也会因故障的不同而呈现不同的约束条件。通过对不同故障下的序电流分量特征进行识别，可判断故障类型与故障相。

2.1 单回线故障时的序分量特征

同塔四回线发生单回线故障时，其余三回线路仍处于正常状态，因此在含有故障线路的双回线分组中，一定含有一条非故障线路。通过该线路的故障边界条件，可推导部分序电流分量之间的关系。当Ⅰ回线发生故障时，Ⅱ回线未发生故障，因此有式（4）的约束条件。所有序电流分量均用相量形式表示。

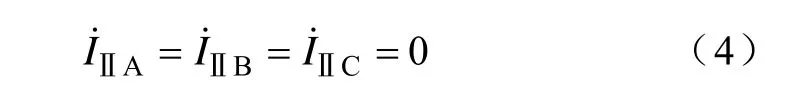
由于序分量电流为相电流的线性组合，因此将式（4）中的相电流替换为序电流分量，可得到I˙e1=I˙f1且I˙e2=I˙f2。即Ⅰ回线发生故障时，不论发生任何类型的故障，在故障点处，e序分量和f序分量的正、负序幅值和相位均对应相等。

当Ⅱ回线故障发生时，相对于Ⅰ回线发生故障，各序电流分量的幅值关系保持不变，仅序电流的相位关系发生变化，即I˙e1=-I˙f1且I˙e2=-I˙f2。

当Ⅲ回线发生故障时，根据边界条件得到I˙g1=I˙h1且I˙g2=I˙h2。当Ⅳ回线故障时，上述各序电流分量的幅值关系保持不变，仅相位关系发生变化。不同回线故障时的典型故障特征见表1。

由表1可看出，发生单回线故障时，正、负序分量中，两组分量e序分量、f序分量和g序分量、h序分量，能分别正确反映出不对称同塔四回线的故障特征。且特征序分量具有良好的幅值和相位关系，因此可通过序电流分量的存在性和幅值、相位关系，确定故障回线。

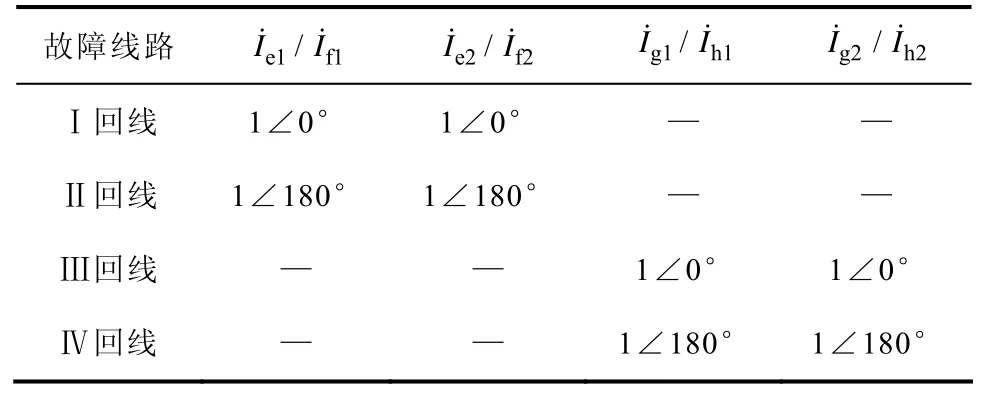
表1 不同回线故障的序分量特征Tab.1 Faulted sequence characteristics of different faulted lines

2.2 故障电流分布系数

线路的保护装置能测量到的电流值通常位于线路的首端或末端，而表1分析的结论为故障点处的电流约束关系，因此需要将故障点处的电流约束关系转变至线路保护装置安装处的电流约束关系，才能根据保护装置所采集的数据进行故障分析。

由线路结构可知，故障点处的故障电流会分解成左、右两支电流分量，分别流向线路首端和末端。由故障序网的结构特点可知，线路首末两端的电流相对于故障点电流，存在一个分布系数，可通过分布系数确定流经保护处的故障电流。而线路两端的分布系数将会影响保护处测量到的序电流分量的幅值和相位，因此必须确定故障分布系数对保护动作、故障选线的影响。

对总长为L的线路，线路单位长度的阻抗为Z'，系统左侧M端的电源阻抗为ZGM，系统右侧N端的电源阻抗为ZGN，故障点距离线路左侧的距离为D，则相对线路左侧的故障位置百分比S=D/ L。对于环流序分量，其故障点左侧的分布系数为

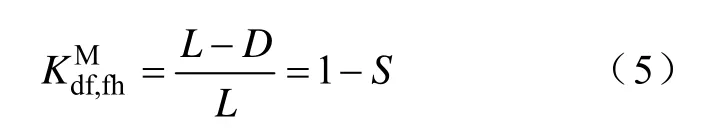
对于穿越序分量，其故障点左侧的分布系数为

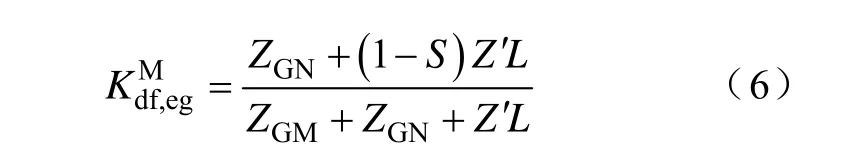
由表1可知，序分量电流以比值关系为主，且同类型序分量间的比值关系会抵消分布系数带来的影响，不同类型序分量间的比值关系为

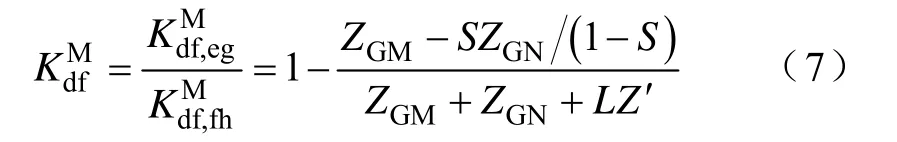
由式（5）可知，环流序分量的分布系数仅受故障点位置的影响且恒为实数，即分布系数只会影响环流序分量的幅值。由式（6）可知，穿越序分量不仅受到故障点位置的影响，同时与系统电源阻抗有关。由式（7）可知，序分量比值不仅受到故障点位置的影响，同时也与系统电源阻抗有关。因此如果将各阻抗作为复数代入穿越序分量的分布系数表达式，则分布系数也为复数，此时分布系数不仅会影响保护处测量的序分量电流的幅值，也会影响序分量电流的相位。

对式（6）和式（7）进行分析可知，当故障分别发生在临近首端与末端时，穿越序分量的分布系数与比值的幅值变化均较大，不利于保护的整定与判断。由于在实际的多回线路中，解耦后线路序阻抗的阻抗角通常大于80°，系统电源的电抗部分也比电阻部分大。即各类阻抗的阻抗角相差不大，因此分布系数对相位的影响较小。

令线路全长的序阻抗为3.437 2+j56.341 6Ω，此时线路阻抗角为86.5°。左、右侧电源的全阻抗幅值分别为80Ω和60Ω。对系统阻抗角为50°和90°两种情况进行仿真，如图1所示，点线表示系统阻抗角为90°的穿越分布系数曲线，实线表示系统阻抗角为50°时的穿越分布系数曲线。

图1 穿越分布系数的相位曲线Fig.1 Phase angle of distribution coefficient

由图1可知，当线路与系统阻抗相位差不大时，穿越分布系数的相位在不同故障位置时变化不大；当线路与系统阻抗角相差较大时，在临近线路首末端发生故障时，穿越分布系数相位发生明显的偏移，但最大偏移角度小于12°。

因此可通过比较保护测量处各序分量电流的相位关系来确定故障线路。为保证保护装置动作的正确性，应设定保护动作的相位阈值，考虑相位偏差，可设定相位整定阈值ΔAng=30°。

2.3 故障选线方法

发生单回线故障时，采用表1中的电流序分量的比值进行故障选线，流程如图2所示，图中采用负序分量进行说明。其中，ΔIF为判定电流序分量是否存在的阈值，用于回避正常运行时的不平衡电流对判定的影响。采用其他序分量的选线流程与图2一致。

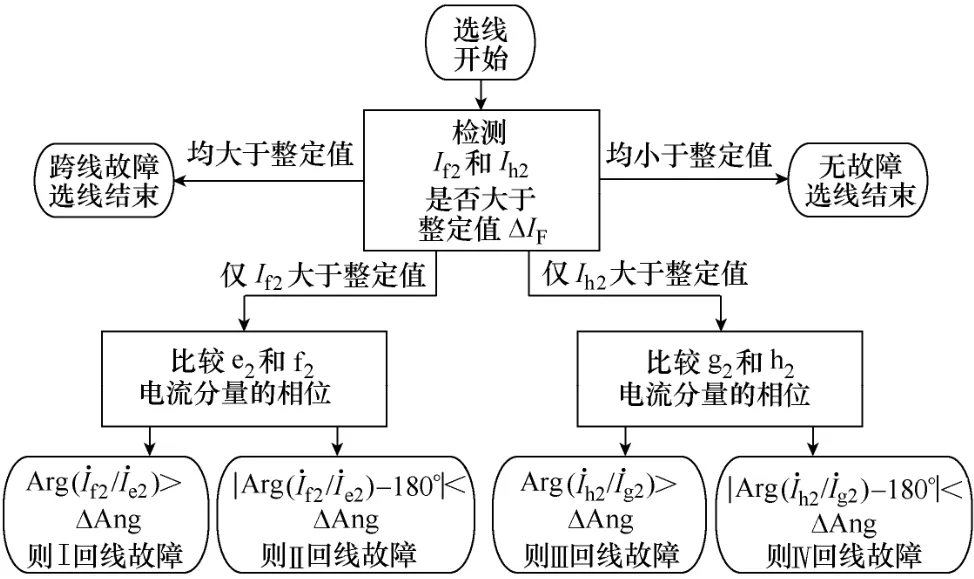
图2 故障选线流程Fig.2 Flow chart of faulted line selection

如图2所示，当检测到故障序分量后，判断f序还是h序分量存在故障电流，进而判断故障存在于Ⅰ、Ⅱ回线还是Ⅲ、Ⅳ回线；再通过穿越序分量与环流序分量比值的相位判断故障发生在哪一回线。当发生故障时，首先判断If2、Ih2与整定值的关系。如果If2越限，则故障出现在Ⅰ、Ⅱ回线上。此时比较Ie2与If2的相位，若相位差约0°，则Ⅰ回线故障；若两者相位差约180°，则Ⅱ回线故障。同理可推出Ih2越限的情况。

3 故障选相原理及方法

3.1 序分量的故障类型特征

在单回线故障时，如Ⅰ回线故障时，列出其余三回线的故障边界条件，则

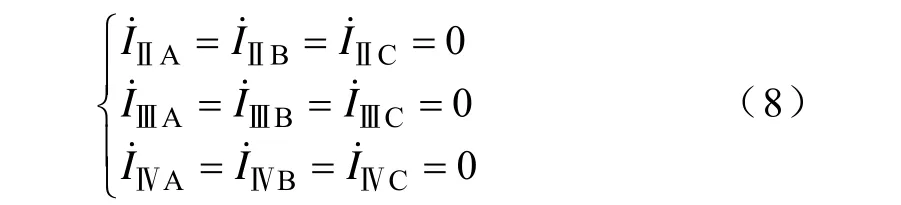
将序分量代入则可得

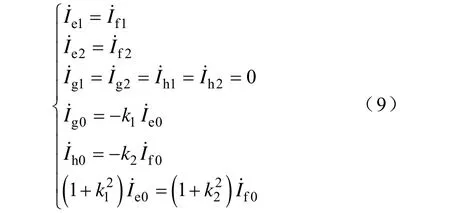
由表1和式（9）可知，正、负和零序分量之间并无明显的约束关系。因此可通过式（10）设定正、负和零序分量的序电流基准值，再根据不同故障类型下，通过基准电流之间的幅值相位关系，推导序电流分量间的关系。以下均以Ⅰ回线故障对各电流序分量进行分析。

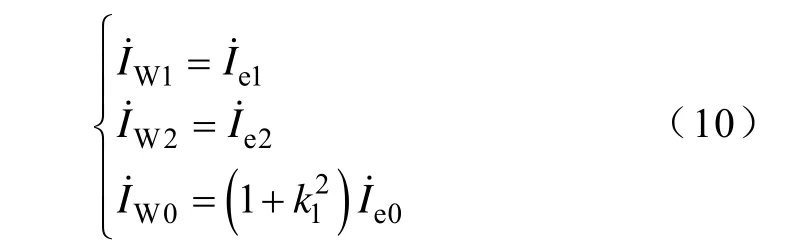
3.2 基于电流幅值的故障识别方法

前文分析得到不同类型故障时，序分量之间的特点。考虑实际运行时的不平衡电流，可得到表2列出的故障类型判据，表中所有数据均为幅值。其中，。

表2 不同故障类型的序分量特征Tab.2 Faulted sequence characteristic of different faulted types

除线路发生三相对称故障外，发生其他类型故障时，故障所在分组的穿越序分量的负序分量一定存在，且数值较大。可通过零序分量鉴别接地故障与相间故障，再通过环流序分量的正、负序电流的幅值，判断单相接地故障与两相接地故障。因此可得到如图3所示的故障类型识别流程。

3.3 基于电流相位的选相方法

由前文可看出，发生单回线故障时，各类序分量中，环流序分量的正序和负序分量有显著的幅值和相位关系。由于故障分布系数对环流量的比值关系无影响，同时为保证故障选相的通用性，因此采用环流序分量的正序和负序的相位关系进行故障选相。当Ⅰ回线发生单回线故障时，不同故障相序与电流序分量之间的关系见表3。

当Ⅱ回线发生故障时，同样可得到表3所列的序电流相位关系。当Ⅲ回线或Ⅳ回线发生故障时，利用Arg（I˙h2I˙h1）进行判断，也能得到类似表3中的结果。发生单回线故障时，故障选相流程如图4所示，其中n为整数。以Ⅱ回线单相接地故障为例，当故障发生时，先利用选线方法判定是Ⅱ回线故障，然后利用故障类型识别方法判定是单相故障，再用f1序与f2序电流相位进行判断，从而得出具体故障相。同理可得到其他回线故障时的判断流程。

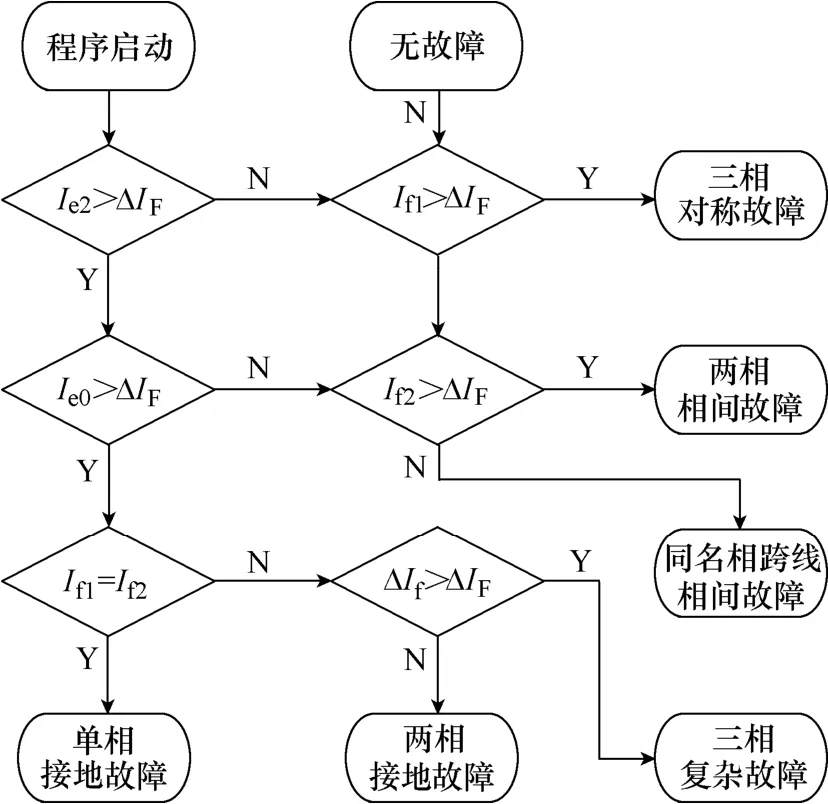
图3 故障类型识别流程Fig.3 Flow chart of faulted type identification

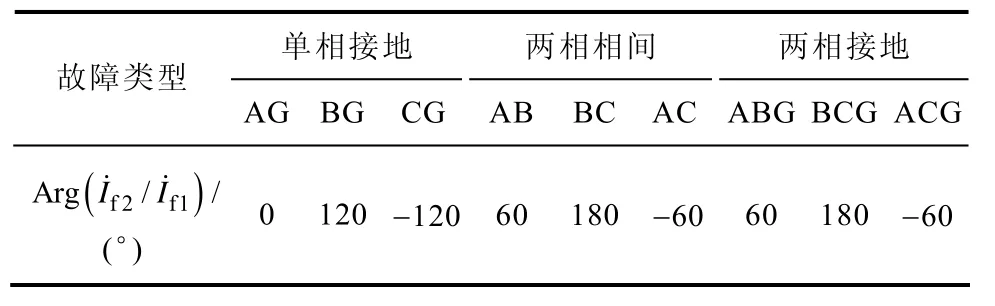
表3 不同故障相的序电流相位关系Tab.3 Angle characteristic of faulted sequence current in different faults

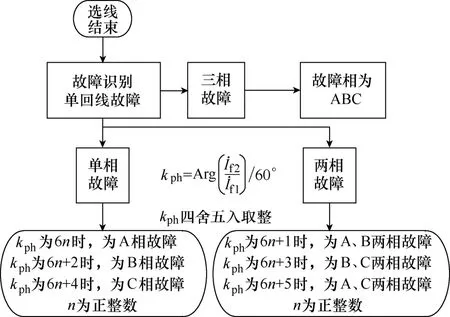
图4 故障选相流程Fig.4 Flow chart of faulted phase selection

4 仿真验证

4.1 仿真线路模型

为验证理论推导得到的故障时各序分量间的关系，采用PSCAD/EMTDP对同塔四回线的各种单回线故障进行仿真。线路模型采用仿真软件的TLine模型，并使用Frequency Dependent （Phase） Model进行仿真。线路换相方式采用仅回线内换相，回线间不换相，其他参数见附录。

4.2 共母线不对称四回线模型仿真

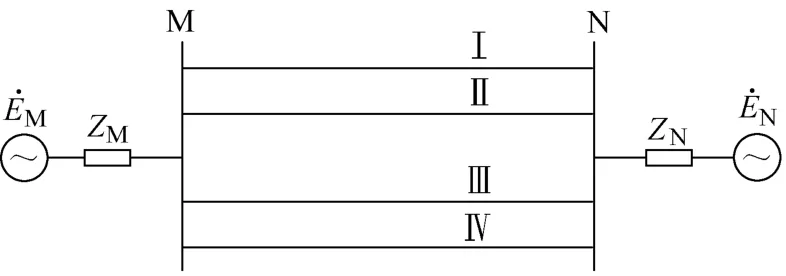
图5 不对称四回线仿真系统结构Fig. 5 System structure of asymmetrical quadruple-circuit transmission lines

线路总长为100km，电压等级为220kV，电源参数与线路参数见附录，仿真系统结构如图5所示。为验证分布系数对测量准确性的影响，仿真选取不同的故障点对故障进行仿真，并设置不同的故障过渡电阻，以验证故障选线、选相的准确性，M侧母线处的仿真结果见表4。

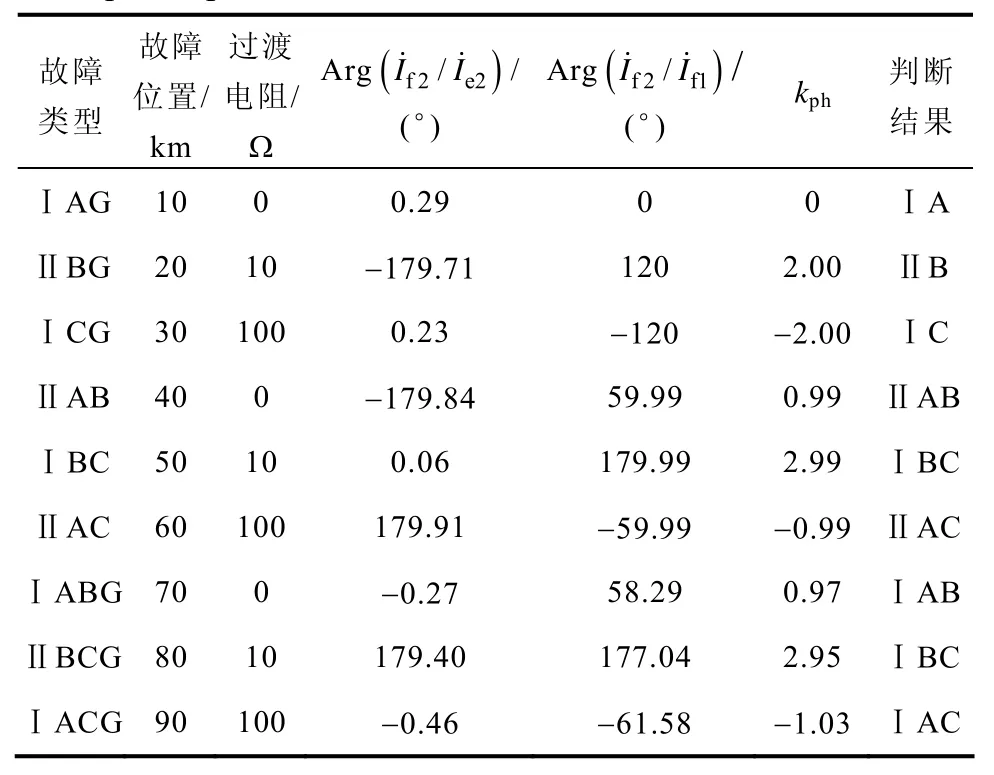
表4 共母线不对称参数四回线仿真结果Tab.4 Simulation results for asymmetrical quadruple-circuit lines connected to the same bus

由表4可看出，故障选线的仿真相位数据非常接近0°或180°，最大误差不超过1°。故障点位置与故障过渡电阻对故障选线方法不会产生影响，具有良好的抗过渡电阻能力和全区间选线能力。

故障选相的仿真数据中，除两相接地故障外，误差都非常小。两相接地故障时，最大误差角度不超过3°，仍能准确进行故障选相。该选线、选相方法可准确地判断故障回线与故障相，能很好地适用于不对称参数的同塔四回线。

4.3 异母线不对称四回线模型仿真

线路总长为100km，电压等级均为220kV，电源参数与线路参数见附录，仿真系统结构如图6所示。

图6 异母线四回线仿真系统结构Fig.6 System structure of asymmetrical quadruple-circuit transmission lines connected to different buses

为验证分布系数对测量准确性的影响，仿真选取不同的故障点对故障进行仿真，并设置不同的故障过渡电阻，来验证故障选线、选相的准确性，M侧母线处的仿真结果见表5。

表5 异母线不对称参数四回线仿真结果Tab.5 Simulation results for asymmetrical quadruple-circuit lines connected to different buses

由表5可看出，故障选线的仿真相位数据非常接近0°或180°，最大误差不超过1°。故障点位置与故障过渡电阻对故障选线方法几乎无影响，具有良好的抗过渡电阻能力和全区间选线能力。

故障选相的仿真数据中，除两相接地故障外，异母线相位计算的各类误差与共母线的误差相近，即误差非常小。两相接地故障时，最大误差角度仍未超过3°，能准确地进行故障选相。该选线、选相方法可准确地判断故障回线与故障相，能很好地适用于跨电压等级的同塔四回线。

4.4 跨线故障仿真

跨线故障仿真的各模型参数与4.2节的各类参数一致，为验证分布系数对测量准确性的影响，仿真选取不同的故障点对故障进行仿真，仿真结果见表6。

当发生跨线对称故障时，会检测出f序或h序电流很小，e序或g序数值较大。此时宜采用e序和g序进行相位验证，由于相位差很小，为统一表示仍使用f序与h序的相位。

表6 共母线不对称参数四回线跨线故障仿真结果Tab.6 Simulation results for asymmetrical quadruple-circuit lines connected to the same bus

由表6的仿真结果可看出，当发生不对称跨线故障时，选线元件测量的相位差接近90°或270°，可判断故障为跨线故障，能准确地识别跨线故障。当发生对称跨线故障时，则需要利用序分量的故障特征鉴别出此类型故障，再利用选相元件进行故障相别的判定。故障点位置对故障选线方法几乎不产生影响，仍具有良好的全区间选线能力。

对于选相元件，当发生跨线两相故障时，按照单回线选相流程选出的为非故障相，即剩余两相发生跨线故障，相序顺序由选线功能测量的相位所决定。即选线测量角为90°时，Ⅰ回线故障相相位滞后Ⅱ回线的故障相，如Ⅰ回线B相存在故障，则判断故障类型为ⅠBⅡA；反之选线测量角为-90°或270°时，Ⅰ回线故障相相位超前Ⅱ回线的故障相，判断故障类型为ⅠBⅡC。

发生跨线故障时，该选线、选相方法需要先对故障类型进行识别，识别后仍能较好地实现不对称参数的同塔四回线的选线、选相功能。

5 结论

1）本文引入相线解耦法对不对称参数的同塔四回线进行解耦，将相电流分解为12个独立的序电流分量，解决了同塔四回线中的解耦问题。

2）本文提出了一种利用单端电气量进行不对称同塔四回线的故障选线、选相方法。先利用故障边界条件和序电流与相电流的关系，得到序电流分量的约束关系方程。然后通过识别f序电流分量和h序电流分量是否越限，来判断故障出现在Ⅰ、Ⅱ回线还是Ⅲ、Ⅳ回线；再利用e序分量、f序分量和g序分量、h序分量的序电流相位特征来判断具体的故障回线，从而实现故障选线。

3）考虑同一回线发生不同类型故障时，序分量电流之间满足固定的幅值关系；同一类型的不同相序故障时，序分量相位差满足特定关系。因而在选线的基础上，先利用幅值关系判断故障类型，再利用相位关系计算kph值，最终判断具体的故障相。

4）论文对不对称同塔四回线的共母线结构与异母线结构进行了仿真验证，仿真结果表明该方法对单回线故障的选线、选相准确，能够很好地适用于不同结构的线路。

5）本文利用故障边界条件推导各序电流的幅值、相位关系，从而进行选线、选相。发生跨线故障时，根据故障类型不同，各序电流的幅值、相位同样存在一定的关系。类比单回线故障，同样可根据故障时序电流幅值、相位的关系进行故障选线、选相。合理地识别跨线故障并完善故障选相方法是本文后续开展的研究工作。

附 录

PSCAD的杆塔结构如附图1所示，其中C1～C3为第一回线，C4～C6为第二回线，C7～C9为第三回线，C10～C12为第四回线。

杆塔的导线使用PSCAD自带的chukar模型进行仿真。通过设置杆塔的空间参数生成线路的阻抗矩阵，其线间自感与互感关系如附图2所示。由附图2可知，顶层两回线的回线内自感与互感相同，底层两回线的回线内自感与互感相同，但顶层两回线与底层两回线的自感与互感不同。仿真系统均采用此杆塔结构进行仿真。

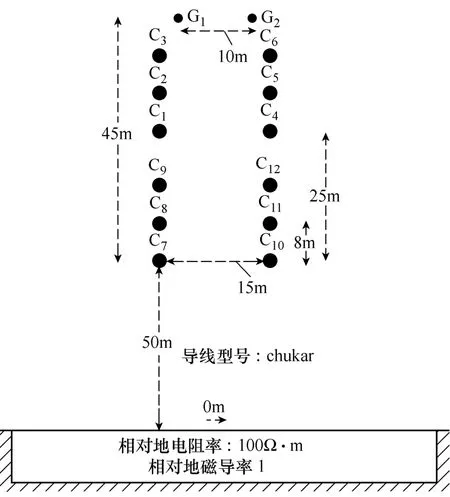
附图1 PSCAD输电线路杆塔模型App. Fig.1 Tower model in PSCAD simulation

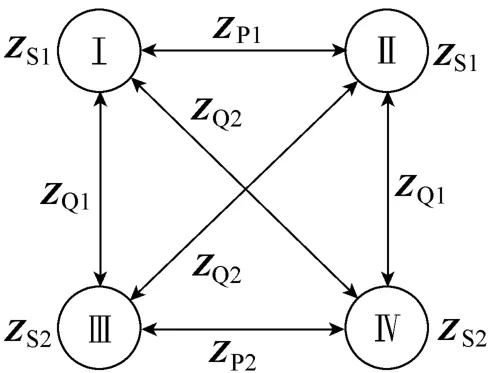
附图2 不对称参数同塔四回线的线间互阻抗App. Fig.2 Mutual impedance between asymmetrical quadruple-circuit transmission lines

不对称四回线模型仿真中，PSCAD电源阻抗部分使用集中参数模型，电源电压为230kV，M端电源的正序阻抗为j6Ω，零序阻抗为0.139 6+j7.998 8Ω，N端电源的正序阻抗为j5Ω，零序阻抗为0.104 7+j5.999 1Ω。线路参数见附表1。

附表1 仿真系统线路阻抗App. Tab.1 Impedance for transmission line

不对称四回线模型仿真中，PSCAD电源阻抗部分使用集中参数模型，电源电压为230kV，M端电源的正序阻抗为j10Ω，零序阻抗为0.209 4+j11.998 2Ω，N端电源的正序阻抗为j8Ω，零序阻抗为0.174 5+j9.998 5Ω。线路参数见附表2。

附表2 仿真系统线路阻抗App. Tab.2 Impedance for transmission line

参考文献

[1] 田羽, 范春菊, 龚振东. 同杆四回线十二序分量法研究[J]. 电力系统自动化, 2007, 31(21): 35-39, 105.

Tian Yu, Fan Chunju, Gong Zhendong. Twelve sequence component method of four-parallel lines on same towers[J]. Automation of Electric Power Systems, 2007, 31(21): 35-39, 105.

[2] 李伟, 毕天姝, 杨奇逊. 基于相关分析的同杆双回线突变量选相新方法[J]. 电力系统自动化, 2011, 35(8): 58-62.

Li Wei, Bi Tianshu, Yang Qixun. Fault phase selection with fault component in same-tower doublecircuit lines based on correlation analysis[J]. Automation of Electric Power Systems, 2011, 35(8): 58-62.

[3] 田羽, 范春菊, 龚震东. 带同杆双回线的T型线路故障分支判定算法[J]. 电力系统自动化, 2006, 30(21): 71-76.

Tian Yu, Fan Chunju, Gong Zhendong. Faulted line selecting method of T circuit of parallel transmission lines[J]. Automation of Electric Power Systems, 2006, 30(21): 71-76.

[4] 陈福锋, 钱国明. 基于同杆双回线跨线故障识别的选相方案[J]. 电力系统自动化, 2008, 32(6): 66-70.

Chen Fufeng, Qian Guoming. Research on fault phase selector of protective relay for double circuit lines based on crossing-line fault identifying[J]. Automation of Electric Power Systems, 2008, 32(6): 66-70.

[5] 葛耀中. 新型继电保护与故障测距原理与技术[M].西安: 西安交通大学出版社, 1996.

[6] 张海, 黄少锋. 利用电压辅助电流选相的同杆双回线单端电气量选相原理[J]. 中国电机工程学报, 2013, 33(7): 139-148.

Zhang Hai, Huang Shaofeng. A fault phase selection scheme of currents with assistant voltages for common-tower double-circuit transmission lines using oneterminal electrical quantities [J]. Proceedings of the CSEE, 2013, 33(7): 139-148.

[7] 王安宁, 陈青, 周占平, 等. 改进的相分量法求解同杆双回线故障新算法[J]. 电力系统自动化, 2009, 33(13): 58-62.

Wang Anning, Chen Qing, Zhou Zhanping, et al. An improved phase component method for calculating faults on the double-circuit transmission lines on same tower[J]. Automation of Electric Power Systems, 2009, 33(13): 58-62.

[8] 田羽, 范春菊, 龚震东. 同杆4回线12序分量法[J].电力系统自动化, 2007, 31(21): 35-39.

Tian Yu, Fan Chunju, Gong Zhendong. Twelve sequence component method of four-parallel lines on same towers[J]. Automation of Electric Power System, 2007, 31(21): 35-39.

[9] Fan Chunju, Liu Ling, Tian Yu. A fault-location method for 12-phase transmission lines based on twelve-sequence-component method[J]. IEEE Transactions on Power Delivery, 2011, 26(1):135-142.

[10] 张琦兵, 邰能灵, 袁成, 等. 同塔四回输电线的相模变换[J]. 中国电机工程学报, 2009, 29(34): 57-62.

Zhang Qibing, Tai Nengling, Yuan Cheng, et al. Phasemode of four-parallel lines on the same tower[J]. Proceedings of the CSEE, 2009, 29(34): 57-62.

[11] 邓孟华, 范春菊, 舒巧俊, 等. 同杆4回线故障选线方法[J]. 电力系统自动化, 2008, 32(15): 57-60.

Deng Menghua, Fan Chunju, Shu Qiaojun, et al. Method for fault line selection of four jointed parallel lines on the same tower[J]. Automation of Electric Power Systems, 2008, 32(15): 57-60.

[12] 邓孟华, 范春菊, 宗明, 等. 基于环流分量的同杆四回线选相方法[J]. 电力系统保护与控制, 2012, 40(1): 138-144.

Deng Menghua, Fan Chunju, Zong Ming, et al. New faulted phase selecting method for four transmission lines on the same tower based on loop flow component[J]. Power System Protection and Control, 2012, 40(1): 138-144.

[13] 徐鹏, 王钢, 李海峰, 等. 基于环流量的同杆四回输电线路故障选线[J]. 电力系统保护与控制, 2011, 38(19): 78-83.

Xu Peng, Wang Gang, Li Haifeng, et al. Fault line selection for four-parallel lines on same tower based on circulation currents[J]. Power System Protection and Control, 2011, 38(19): 78-83.

[14] 龚震东, 范春菊, 田羽. 一种适合于同杆4 回线的故障测距方法[J]. 电力系统自动化, 2007, 31(23): 70-73.

Gong Zhendong, Fan Chunju, Tian Yu. A fault location algorithm suitable for jointed four transmission lines[J]. Automation of Electric Power Systems, 2007, 31(23): 70-73.

[15] 任明珠, 吴文宣, 陈金祥, 等. 基于负序电流的同塔多回线故障测距方法[J]. 电力系统及其自动化学报, 2010, 22(1): 71-75.

Ren Mingzhu, Wu Wenxuan, Chen Jinxiang, et al. New fault location algorithm for muti-loop transmission lines based on negative-sequence current[J]. Proceedings of the CSU-EPSA, 2010, 22(1): 71-75.

[16] 舒巧俊, 陈松石, 范春菊, 等. 非全程同杆四回线故障选线新方法[J]. 电力系统保护与控制, 2010, 38(19): 131-136.

Shu Qiaojun, Chen Songshi, Fan Chunju, et al. A new method of fault line selection for incomplete-journey four-jointed parallel line on the same tower[J]. Power System Protection and Control, 2010, 38(19): 131-136.

[17] 李博通, 李永丽, 陈莉, 等. 同塔四回线参数解耦及故障分析方法[J]. 电力系统保护与控制, 2010, 38(19): 2-9.

Li Botong, Li Yongli, Chen Li, et al. Method for parameter decoupling and fault analysis of fourcircuit transmission lines on the same tower[J]. Power System Protection and Control, 2010, 38(19): 2-9.

[18] 宋国兵, 李森. 一种新相模变换矩阵[J]. 电力系统自动化, 2007, 31(14): 57-60.

Song Guobing, Li Sen. A novel phase-mode transformation matrix[J]. Automation of Electric Power System, 2007, 31(14): 57-60.

刘 琦 男，1987年生，博士研究生，研究方向为电力系统保护与控制。

E-mail: LiuQi8165@163.com（通信作者）

邰能灵 男，1972年生，教授，博士生导师，主要从事电力系统保护与控制及电力市场方向的教学与研究。

E-mail: nltai@sjtu.edu.cn

作者简介

收稿日期2014-01-16 改稿日期 2014-09-09

中图分类号：TM773