扩展卡尔曼滤波的目标跟踪优化算法

宁倩慧，张艳兵，刘　莉，陆　真，郭冰陶

(1.中北大学电子测试技术重点实验室，山西 太原 030051；

2.中北大学仪器科学与动态测试教育部重点实验室，山西 太原 030051)



扩展卡尔曼滤波的目标跟踪优化算法

宁倩慧1,2，张艳兵1,2，刘莉1,2，陆真1,2，郭冰陶1,2

(1.中北大学电子测试技术重点实验室，山西 太原 030051；

2.中北大学仪器科学与动态测试教育部重点实验室，山西 太原 030051)

摘要:针对传统扩展卡尔曼滤波算法在多普勒量测目标跟踪情况下估计精度低的问题，提出了扩展卡尔曼滤波目标跟踪优化算法。该算法对传统的扩展卡尔曼滤波算法进行了改进，将仅考虑位置量测的扩展卡尔曼滤波算法推广到包含多普勒量测的算法以提高目标跟踪精度。仿真结果表明，该算法具有较小的均方根位置误差和均方根速度误差，可以很好地提高目标跟踪过程中的精度，可有效应用于机动目标跟踪场合。

关键词:扩展卡尔曼滤波；目标跟踪；多普勒量测；跟踪精度

0引言

目标跟踪是雷达数据处理的关键部分，随着新型雷达和新概念雷达的不断出现，信号处理能力迈上了一个新的台阶[1-2]，使得雷达数据处理的信息量越来越大，对目标跟踪算法提出了更高的要求[3-4]。

很多情况下，观测数据和目标动态参数间的关系是非线性的[5]，常用的非线性滤波方法有扩展卡尔曼滤波、不敏卡尔曼滤波[6]、粒子滤波[7]。在这三种跟踪算法中，扩展卡尔曼滤波速度最快，不敏卡尔曼滤波次之，最慢的是粒子滤波[8-9]。扩展卡尔曼滤波不仅具有计算量小的优点，也具有统计有效的优点[4]。但在雷达提供多普勒量测时，扩展卡尔曼滤波的效果就会变差，大大降低了目标的跟踪精度[10]。而实践结果表明，充分利用雷达的多普勒量测信息可以有效提高目标的跟踪精度[11]。针对以上问题，本文提出了扩展卡尔曼滤波的优化算法。在斜距误差和多普勒误差相关的情况下[12]将扩展卡尔曼滤波推广到包含多普勒量测的情况。

1传统的扩展卡尔曼滤波

扩展卡尔曼滤波是利用泰勒级数展开方法将非线性滤波问题转化成近似的线性滤波问题，利用线性滤波的理论求解非线性滤波问题的次优滤波算法。其系统的状态方程和量测方程分别如式(1)、式(2)所示：

X(k+1)=f(k,x(k))+v(k)

(1)

Z(k)=h(k,X(k))+W(k)

(2)

式中，X(k)为n维的随机状态向量序列，Z(k)为n维的随机量测向量序列，f(k,x(k))为空气阻力，v(k)、w(k)为零均值的正态(高斯)白噪声序列，其方差分别满足：

(3)

(4)

协方差的一步预测为：

(5)

量测预测值为：

(6)

相应的协方差为：

S(k+1)=

(7)

增益为：

(8)

状态更新方程为：

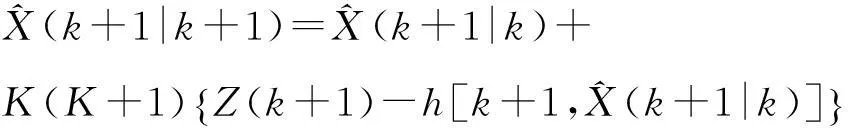
(9)

协方差更新方程为：

p(k+1|k+1)=

[I-K(k+1)hx(k+1)]p(k+1|k)·

[I+K(k+1)hx(k+1)]′-

K(k+1)R(k+1)K′(k+1)

(10)

式中，I为与协方差同维的单位矩阵。

二阶扩展卡尔曼滤波的泰勒展开保留到二阶项，其状态的一步预测为：

(11)

协方差的一步预测为：

量测预测值为：

(12)

相应的协方差为：

S(k+1)=hx(k+1)p(k+1|k)·

(13)

增益为：

(14)

状态更新方程为：

(15)

协方差更新方程为：

p(k+1|k+1)=[I-K(k+1)hx(k+1)]·

p(k+1|k)[I+K(k+1)hx(k+1)]′-

K(k+1)R(k+1)K′(k+1)

(16)

式中，I为与协方差同维的单位矩阵。

2扩展卡尔曼滤波优化算法

研究表明，在很多情况下，斜距和多普勒量测误差是统计相关的，为充分利用雷达的多普勒量测信息，本文提出扩展卡尔曼滤波的优化算法，在考虑斜距误差和多普勒误差相关性的情况下将多普勒量测包含进去。该算法的状态方程可表示为：

(17)

由于位置转换量测是目标运动状态的线性函数，所以采用序贯滤波估计线性函数，去除位置和估计量测之间的相关性。将协方差阵Ra(k)按位置和估计量测两部分分块可表示为：

(18)

令

(19)

由矩阵的Cholesky分解可得

(20)

式中，

(21)

利用式(17)、式(20)，可以完成对目标运动状态的滤波估计，主要包括以下四个步骤：

步骤一：时间更新滤波估计

(22)

步骤二：位置量测更新滤波估计

(23)

步骤三：伪量测更新滤波估计

(24)

步骤四：最终滤波估计：

(25)

算法的仿真流程如图1所示。

3仿真结果及分析

3.1仿真条件

3.2仿真结果

采用两点差分法对滤波器进行初始化，评价指标分别是均方根位置误差和均方根速度误差，将传统扩展卡尔曼滤波算法与优化算法进行对比，在步长30的情况下仿真500次，实验在MATLAB7.6.0上进行，仿真结果如图2-图5所示。

3.3仿真结果分析

从图2可以看出，优化算法对目标的跟踪性能明显高于传统算法。传统算法在前几个仿真步长里位置均方根误差较大，后来快速收敛，优化算法的目标均方根位置误差和均方根速度误差均小于传统算法。

图1　优化算法的仿真流程图Fig.1　The simulation flow chart of optimization algorithm

序号初始状态X(0)/(m,m/s,m,m/s)测距误差σp/m测角误差σθ/mrad测速误差σp·/(m/s)1(10000,30,10000,30)150512(100000,30,100000,30)150513(10000,30,10000,30)50514(100000,30,100000,30)150401

图2　序号1情况下仿真图Fig.2　The simulation map of No.1

从图3对比可以发现，当目标距离远时，优化算法较传统算法的位置误差和均方根较小，且在15步长以后两种算法的速度误差相差无几。结合图2的结果可以发现当测距误差、测角误差和测速误差一样的情况下，距离越远，跟踪精度越低。

图3　序号2情况下仿真图Fig.3　The simulation map of No.2

从图4可以看出，在目标测距精度高的情况下，优化算法的跟踪精度明显优于传统算法，结合图3的结果可以发现测速精度与测距精度的比例关系也影响着跟踪精度，且比例越大，精度越高。

图4　序号3情况下仿真图Fig.4　The simulation map of No.3

从图5的结果可以看出，在距离较远，测角误差较大的情况下，优化算法的跟踪精度明显优于传统算法，说明，利用测速信息并不能改善跟踪精度。结合图3的结果可知测角误差和测距误差的比例影响着跟踪精度，且该比例越大，跟踪精度越高。结合图2的结果可知，在目标距离、测距误差和测速误差一样的情况下，测角误差越大，跟踪效果越好。

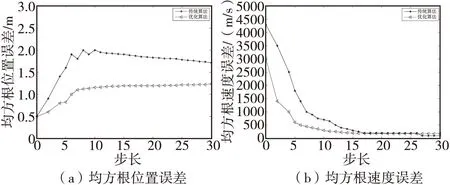
图5　序号4情况下仿真图Fig.5　The simulation map of No.4

综上所述，在包含多普勒量测的情况下，优化算法优于传统扩展卡尔曼滤波算法。

4结论

本文提出了扩展卡尔曼滤波在目标跟踪方面的优化算法，该算法对传统的扩展卡尔曼滤波算法进行了改进，将仅考虑位置量测的扩展卡尔曼滤波算法推广到包含多普勒量测的算法以提高目标跟踪精度。仿真结果表明，提出算法具有较小的均方根位置误差和均方根速度误差，可以很好地提高目标跟踪过程中的精度，可有效应用于机动目标跟踪场合，具有广阔的应用前景。

参考文献:

[1]毛二可,龙腾,韩月秋.频率步进雷达数字信号处理[J].航空学报，2001,22(6)：16-20.

[2]刘兴钊.数字信号处理[M].北京：电子工业出版社,1992.

[3]强勇,张冠杰,李斌.MIMO雷达进展及其应用研究[J].火控雷达技术,2010,39(1):1-10.

[4]何友,修建娟,关欣.雷达数据处理及应用[M].北京：电子工业出版社，2013.

[5]陈咏梅,潘泉,张洪才，等.基于推广卡尔曼滤波的多站被动式融合跟踪[J].系统仿真学报，2003,15(4)：521-524.

[6]刘德春,谭信.非线性滤波算法性能对比[J].电子设计工程,2011,19(13):49-51.

[7]胡士强,敬忠良.粒子滤波算法综述[J].控制与决策,2005,20(4)361-366.

[8]潘勃,冯金富,李骞.毫米波/红外多传感器融合跟踪算法研究[J].红外与毫米波学报,2012，29(3):230-235.

[9]杨永健,樊晓光,王晟达，等.基于修正卡尔曼滤波的目标跟踪[J].系统工程与电子技术，2014,36(5):846-851.

[10]曹洁,文如泉.IMM-UPF算法在机动目标跟踪中的研究[J].计算机工程与应用,2010,46(28):240-243.

[11]Hall D L.Mathematical Techniques in Multi-sensor Data Fusion[M].Artech House,Boston,London,1992.

[12]Bar-Shalom Y, Negative Y.Correlation and Optical Tracking with Doppler Measurement[J].IEEE Transaction on Aerospace and Electronic System,2001，37(3):1117-1120.

Optimization Algorithm for Target Tracking Based on Extended Kalman Filtering

Ning Qianhui1,2，Zhang Yanbing1,2，Liu Li1,2，Lu Zhen1,2，Guo Bingtao1,2

(1.Science and Technology on Electronic Test&Measurement Laboratory, North University of China,Taiyuan ,030051, China;2.Key Laboratory of Instrumentation Science & Dynamic Measurement of Ministry of Education,North University of China,Taiyuan ,030051,China)

Abstract:Aiming at the problem that the estimation precision of traditional extended kalman filter algorithm in target tracking with doppler measurement is low , this paper puts forward an optimization algorithm for target tracking based on extended kalman filtering. To realize the target tracking accuracy, the algorithm makes some improvements on the traditional extended kalman filtering,and extended the traditional algorithm only consider the positon measurement to doppler measurement. Simulation results indicate that the proposed algorithm has smaller root mean square position error and root mean square velocity error,and can well enhance the target tracking accuracy. So it can be effectively applied to maneuver target tracking.

Key words:extended Kalman filter; target tracking; Doppler measurement; tracking accuracy

中图分类号:TP802.2

文献标志码:A

文章编号：1008-1194(2016)01-0090-05

作者简介:宁倩慧(1990—)，女，山西运城人，硕士研究生，研究方向：动态测试与智能仪器，信号与信息处理。E-mail：qian5_6@163.com。

*收稿日期:2015-09-28