平面曲折槽机构参数与结构阻尼系数关系模型

唐志成，席占稳，聂伟荣，周织建，张星星

(南京理工大学机械工程学院，江苏 南京 210094)



平面曲折槽机构参数与结构阻尼系数关系模型

唐志成，席占稳，聂伟荣，周织建，张星星

(南京理工大学机械工程学院，江苏 南京 210094)

摘要:针对传统曲折槽研究过分依靠仿真的问题，提出了曲折槽机构参数与结构阻尼系数关系模型。该模型建立了弹簧-质量-阻尼系统，分析了结构阻尼系数与载荷区分性能的关系，并根据结构阻尼系数与上升时间的关系推导出了曲折槽参数对于结构阻尼系数的影响趋势。通过ANSYS仿真与MATLAB曲线拟合，验证了以上推导的正确性。结果表明，当曲折槽倾角或锚槽间隙较小时(槽倾角2α<82.5°，锚槽间隙h<0.02 mm)，结构阻尼系数c随槽倾角、锚槽间隙增大呈递减趋势；当2α趋近于90°、h趋近于0.05时，阻尼系数c随着参数的增大而逐渐递增；当槽倾角或锚槽间隙进一步增大时，阻尼系数c随着参数的增大而持续减小。

关键词:平面曲折槽；结构阻尼系数；弹簧-质量-阻尼系统；槽倾角；锚槽间隙

0引言

曲折槽机构作为一种常见时间延迟机构，被广泛运用在各种引信的解除保险机构上[1-3]。其工作原理是通过开有导槽的惯性筒与锚销相碰撞来实现延时功能[4]。平面曲折槽机构是在传统曲折槽机构的基础上结合MEMS技术设计而成的。文献[5]对仿真结果进行分析得出，在一定范围内增大惯性筒上曲折槽宽度、曲折槽拐角处圆角及曲折槽深度均有利于曲折槽机构解除保险，反之则有利于勤务处理安全性。文献[6]着重研究了平面微曲折槽，分析了曲折槽段数、曲折槽倾角、锚槽间隙等参数对于机构识别勤务跌落与正常发射环境性能的影响。以上文献是基于对仿真结果的分析来阐述曲折槽参数对于机构环境响应性能的影响，并未从二阶系统的角度来分析。本文针对此问题，提出了平面曲折槽机构参数与结构阻尼系数关系模型。

1平面曲折槽机构工作原理

图1所示是一种带平面曲折槽机构的惯性响应系统的初始状态。开始时固定锚销处在质量块第一个齿内，质量块通过弹簧与固定体连接，在受向上的加速度时会沿敏感方向运动并与固定锚销碰撞。碰撞过程会改变质量块的速度，造成动能损耗的同时延缓了质量块的运动，当所受载荷为小脉宽高幅值信号时，由于载荷作用时间较小，质量块不能完全运动到位，当所受载荷为大脉宽低幅值信号时，质量块可以最终运动到位并解除保险。

图1　平面曲折槽机构Fig.1　Planar Tortuous Groove Agency

2关系模型建立与分析

对于图1所示的平面曲折槽机构，其物理模型可以用图2所示的弹簧-质量-阻尼系统来表示。其数学模型为：

(1)

其中m为质量，k为弹簧刚度，c为系统综合阻尼，u为质量块位移，F为系统所受外力。包括结构阻尼和摩擦阻尼。为简化设计，本文只考虑结构阻尼。

这是一个典型的二阶系统，对该二阶欠阻尼系统施加一个单位阶跃激励信号，可以得到响应信号，响应曲线从零时刻开始，首次到达稳态的时间与阻尼相关，称为上升时间，可以表示为[7]：

(2)

从式(2)可知，响应曲线的上升时间t与结构阻尼系数c呈正相关，结构阻尼系数c越大，响应曲线的上升时间t越长。这在载荷为一般阶跃信号时仍旧适用。

图2　质量-弹簧-阻尼系统的理论模型Fig.2　The Theoretical Model of Mass-spring-damper System

该平面曲折槽机构在受到一个阶跃载荷时，质量块先沿着载荷方向加速运动，在T0时刻发生第一次碰撞，经过t1时间发生第二次碰撞，以此类推，随着碰撞次数的增多，质量块运动距离随之增大，在T时刻曲折槽全部通过固定锚销，最终质量块的位移为ma/k，将此时质量块所处位置称为稳定位移位置。为简化研究，将运动质量块与固定锚销的碰撞简化成运动锚销与固定质量块的碰撞；曲折槽如图3所示，其中R为锚销直径，S为曲折槽齿面斜边长，h为锚槽间隙，2α为曲折槽倾角。碰撞过程中的能量损失用速度的改变量表示，碰撞后的速度大小为碰撞前的β倍，0<β<1 。忽略碰撞中因摩擦造成的速度方向的不规则变化，碰撞前后速度方向的变化遵循反射规律。

通过研究质量块与锚销的碰撞过程，按碰撞顺序关系将碰撞过程分为以下三类：对边碰撞，邻边碰撞，跳跃碰撞。这三类碰撞过程分别如图4—图6所示。

图4　对边碰撞过程图 Fig.4　Opposite Side Collision Diagram

图5　邻边碰撞过程图Fig.5　Adjacent Side Collision Diagram

图6　跳跃碰撞过程图Fig.6　Jump Collision Diagram

本文研究只考虑质量块与锚销三种碰撞都发生的情形，建立一个与碰撞面1相关的坐标系，如图4，与碰撞面1平行的方向向量为p和与碰撞面1垂直的方向向量为q。未碰撞前速度为V1，在T1+δ时刻碰撞结束，此时的速度为V1+δ,对速度进行分解，可以得到：

(3)

从T0时刻开始，经过t1时间，锚销与曲折槽壁碰撞面2发生碰撞,碰撞间隔时间t1为：

(4)

式(4)中a为加速度，从式(4)可以知道，当倾角或者锚槽间隙增大时，t1增大。平行于碰撞面1的位移为：

(5)

当曲折槽齿面斜边长为定值时，运动完一个斜面所需对边碰撞次数η为：

η=S/φL

(6)

式(6)中，φ为速度修正系数，由式(5)、(6)可知，对边碰撞的次数η与时间t1的二次函数呈负相关，当倾角或者锚槽间隙与锚销直径比值很小时，对边碰撞的次数远大于邻边碰撞和跳跃碰撞。

建立一个与碰撞面2相关的坐标系，如图5，与碰撞面2平行的方向向量为k，与碰撞面2垂直的方向向量为j。在T2时刻即将发生碰撞，此时的速度为V2，根据之前的假设，碰撞过后的速度为：

(7)

两次碰撞的间隔时间为：

(8)

从式(8)可知，t2随倾角增大而增大。

图6中第一次碰撞后的速度V1+δ在X-Y垂直坐标系内的速度为：

V1+δ=-βV1sin2α·x-βV1cos2α·y

(9)

图中两次碰撞间隔时间为t3，其竖直位移随锚槽间隙增大而增大，时间t3为：

(10)

从式(10)可知，当倾角增大时，时间t3减小，当锚槽间隙增大时，时间t3增大。

通过观察仿真运动过程，对比三种碰撞类型可知，对边碰撞时位移最小，邻边碰撞次之，跳跃碰撞时位移最大。

质量块运动距离第一次到达稳态位移位置时间为t，这段时间内对边碰撞，邻边碰撞及跳跃碰撞的次数为η1,η2,η3。

t=t0+η1φ1t1+η2φ2t2+η3φ3t3

(11)

式(11)中，φ1，φ2，φ3为速度修正系数,因为每次碰撞初速不相同，需对速度修正。

当倾角小于2α1或者锚槽间隙与锚销直径小于h1/R时，对边碰撞的次数远大于邻边碰撞和跳跃碰撞，此时的上升时间变化主要由对边碰撞决定。式(11)可以简化为：

t=t0′+η1φ1t1

(12)

式(12)中，t0′为其余碰撞过程时间的总和，可看成恒定值，当倾角或者锚槽间隙增大时，t1增大，又因η1与时间的二次函数呈负相关，所以η1减小，上升时间t减小。因结构阻尼系数与上升时间呈正相关，所以结构阻尼系数也减小。

当倾角大于2α1或锚槽间隙与锚销直径比大于h1/R时，对边碰撞次数不再远大于邻边碰撞和跳跃碰撞，此时对边碰撞次数与时间都很小，对上升时间的影响不大，邻边碰撞次数大于跳跃碰撞，上升时间的改变由邻边碰撞和跳跃碰撞决定。式(11)可以简化为：

t=t″0+η2φ2t2+η3φ3t3

(13)

式(13)中t0″为其余碰撞过程时间的总和，可看成一个恒定值，倾角增大时，t2增大，t3减小，由于φ2大于φ3，所以总的上升时间t依旧增大，结构阻尼系数增大。当锚槽间隙增大时，t2不变，t3增大，所以总的上升时间t增大，结构阻尼系数增大。

当倾角大于2α2或锚槽间隙与锚销直径比值大于h2/R后，对边碰撞的次数减小。此时，随着倾角或锚槽间隙的增大，邻边碰撞次数减小，跳跃碰撞次数缓慢增大。上升时间的改变由三个碰撞过程共同决定，上升时间表达式如式(11)所示。随着倾角或锚槽间隙增大，η1，η2逐渐减小，η3逐渐增大，因为每增加一次跳跃碰撞，至少减小一次对边碰撞和邻边碰撞。所以跳跃碰撞增加的次数少于对边碰撞和领边碰撞减小的次数，而单次跳跃碰撞时间一定小于对边碰撞和邻边碰撞时间之和，所以此时不论t3如何变化，总的上升时间t减小，结构阻尼系数减小。

综上所述，结构阻尼系数和曲折槽参数的关系可以通过图7来表示。

3仿真验证与曲线拟合

为验证理论分析的正确性，需对该平面曲折槽机构进行ANSYS瞬态动力学仿真。机构的整体结构如图1所示，其中弹簧的参数如表1所示，曲折槽及质量块的参数如表2所示。

图7　结构阻尼系数和曲折槽参数的关系Fig.7　The Relation Curve between the Structural Damping Coefficient and the damping characteristics

位移的稳态值是由弹簧刚度、质量块质量及加载载荷共同决定。为保证最终稳态值不在曲折槽段，给系统施加一个20 000的阶跃载荷，由二阶系统瞬态响应可知，最终系统趋于稳定时的位移量为：

1.199×10-3m，该稳定值大于曲折槽段的长度，满足要求。

表1　弹簧的结构参数

表2　曲折槽及质量块结构参数

将模型导入ANSYS中进行瞬态动力学仿真，加载曲线如图8所示。最终得出质量块在载荷敏感方向的仿真位移曲线如图9所示。

把仿真得到的时间与位移的数据导入到MATLAB中，设定该二阶响应函数的其他参数值，即质量m与弹簧刚度k的值，使用MATLAB软件对曲线进行step函数多次拟合，将仿真值与拟合值的误差取绝对值后累加，最终得出绝对误差最小时的结构阻尼系数c。拟合的曲线与仿真曲线对比图如图10所示。

图8　仿真加载曲线Fig.8　Simulation Loading Curve

图9　仿真位移曲线Fig.9　Simulation Displacement Curve

图10　仿真位移曲线与拟合曲线图Fig.10　The Simulation DisplacementCurve and the Fitting Curve Graph

该二阶系统的结构阻尼系数为：0.076 5。二阶系统的传递函数为：

对系统施加如图11所示的两个不同载荷，载荷一为高幅值小脉宽载荷，载荷二为低幅值大脉宽载荷。使用MATLAB软件可以得出系统的位移响应曲线如图12所示。

由图12可知，二阶系统对于小脉宽高幅值载荷的位移响应曲线最大值小于系统对于大脉宽低幅值载荷的位移响应曲线最大值。

将曲折槽机构的其他参数固定，分别仿真不同槽倾角时的情形，最终拟合出的结构阻尼系数结果如表3所示。

图13为表3中结构阻尼系数与槽倾角的关系曲线。

图11　两种不同的加载曲线Fig.11　Two Different Loading Curve

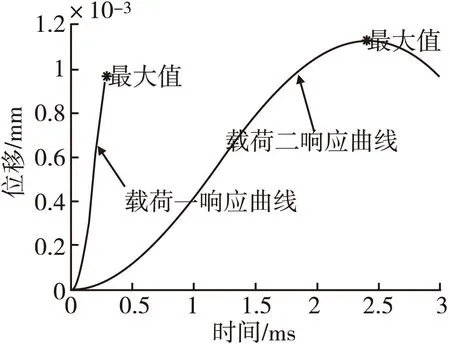
图12　系统对于不同载荷的响应曲线Fig.12　System Response Curves for Different Loads

图13　结构阻尼系数与槽倾角的关系曲线Fig.13　The Relation Curve between the Structural Damping Coefficient and Groove Inclination

由图13可知，随着槽倾角2α的增大，结构阻尼系数c快速减小，当槽倾角增大到82.5°时，阻尼系数达到一个局部极小值0.0384；之后随着倾角增大，阻尼系数随之增大，当倾角达到85°时，阻尼系数为0.0664；之后随着倾角增大，阻尼系数逐渐减小。

将曲折槽其他参数固定，分别仿真不同锚槽间隙时的位移曲线，最终拟合出的结构阻尼系数结果如表4所示。

表3　不同倾角时的结构阻尼系数

表4　不同h/R时的结构阻尼系数

图14为表4中结构阻尼系数与锚槽间隙与锚销直径之比的关系曲线。

图14　锚槽间隙与结构阻尼系数的关系曲线Fig.14　The Relation Curve between the Structural Damping Coefficient and Anchor Groove Gap

由图14可知：当其他参数固定时，结构阻尼系数随锚槽间隙与锚销直径之比的增大急剧减小，当锚槽间隙与锚销直径之比为0.1时，结构阻尼系数达到局部极小值0.025 6；之后随着锚槽间隙与锚销直径之比增大，阻尼系数逐渐增大，当锚槽间隙与锚销直径之比为0.25时，结构阻尼系数达到局部极大值为0.058 8；之后，随着锚槽间隙与锚销直径之比的增大，结构阻尼机构的结构阻尼系数慢慢减小。

4结论

本文把曲折槽机构转化成一个二阶系统，提出了一种曲折槽机构参数与结构阻尼系数关系模型，该模型分析了曲折槽结构阻尼系数与载荷区分性能的关系，推导出曲折槽不同参数对于曲折槽机构阻尼系数的影响，再通过建模仿真及曲线拟合加以验证。结果表明，当曲折槽倾角或锚槽间隙较小时(槽倾角2α<82.5°，锚槽间隙h<0.02mm)，结构阻尼系数c随槽倾角、锚槽间隙增大呈递减趋势；当2α

趋近于90°、h趋近于0.05时，阻尼系数c随着参数的增大而逐渐递增；当槽倾角或锚槽间隙进一步增大时，阻尼系数c随着参数的增大而持续减小。拟合出的阻尼系数曲线能够很好地验证曲折槽倾角及锚槽间隙对于系统阻尼系数的影响趋势，对曲折槽机构载荷识别区分的研究具有重要的指导意义。

参考文献:

[1]檀永杰.引信曲折槽后坐保险机构理论研究[D].南京：南京理工大学,2008.

[2]梁医，张明宏，陈荷娟，引信曲折槽机构摩擦系数检测模型及其求解[J].南京理工大学学报，2005，29(6)：666-668.

[3]谭惠民，齐杏林．曲折槽机构的灵敏度分析[J]．兵工学报，1994，(4)：66-69.

[4]王辉，陈荷娟. 复合式惯性制动保险机构及性能分析[J]．探测与控制学报，2007，29(1)：32-35.

[5]程君，闻泉，王雨时，等.引信曲折槽机构设计参数灵敏度[J].探测与控制学报，2014，36(4)：9-13.

[6]薛维清.引信用微机电惯性接电开关设计[D].南京：南京理工大学,2013.

[7]董景新，赵长德，郭美凤.控制工程基础[M].北京：清华大学出版社，2009.

Coefficient Model of the Parameters of Planar Tortuous Groove and Damping

TANG Zhicheng, XI Zhanwen , NIE Weirong, ZHOU Zhijian, ZHANG Xingxing

(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

Abstract:For the previous research of tortuous groove relying too much on simulation, a relational model between the parameters of planar tortuous groove and damping coefficient was proposed. A spring-damper-mass system was built and the relationship between damping coefficient and distinguishing performance of the loading was analyzed. According to the relationship between damping coefficient and transient response rise time, the impact of the tortuous groove inclination and anchor groove gap to damping coefficient was derived and it has been well verified by ANSYS simulating and MATLAB curve fitting. The results showed that when tortuous groove inclination and the anchor groove gap increases, damping coefficient was first decreased then increased and decreased after reaching the maximum.

Key words:planar tortuous groove; spring-damper-mass system; groove inclination; anchor groove gap; damping coefficient

中图分类号:TJ430

文献标志码:A

文章编号：1008-1194(2016)01-0047-05

作者简介:唐志成(1991—)，男，安徽当涂人，硕士研究生，研究方向：微机电系统设计。E-mail:tangjurry@163.com。

*收稿日期:2015-08-27