一道高考试题结论的引申与探究
一道高考试题结论的引申与探究
湖南省浏阳市第一中学1309班(410300)罗邯
1.考题再现
2014年四川省高考数学卷理科第20题

(1)求椭圆C的标准方程;
(2)设F为椭圆C的左焦点,T为直线x=-3上任意一点,过F作TF的垂线交椭圆C于点P,Q.
(ⅰ)证明:OT平分线段PQ(其中O为坐标原点);

对于第(1)问,易求得椭圆C的标准方程为
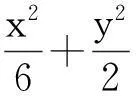
2.引申与探究
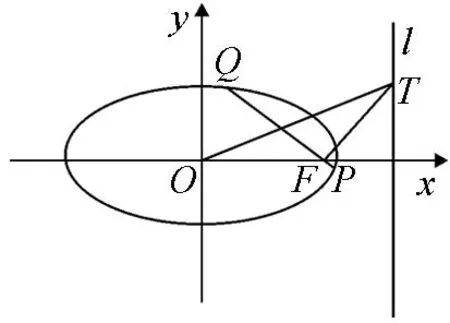
图1

(1)若y0=0,则线段PQ垂直于x轴,显然OT平分线段PQ.
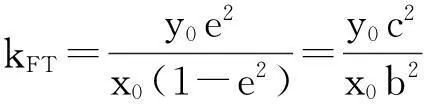


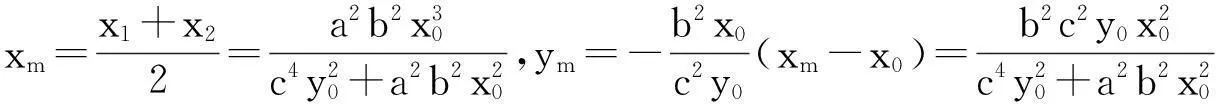
综合(1)、(2)可得结论成立.
显然,若x0=c(或-c),则定点F和定直线l分别是椭圆的焦点和准线.
上述结论能否类比到双曲线上呢?答案是肯定的.于是就有如下的结论:

图2
证明方法与结论1的类似,本文不再赘述.
同样,若x0=c(或-c),则定点F和定直线l分别是双曲线的焦点和准线.
椭圆和双曲线称为有心圆锥曲线,而抛物线则称为无心圆锥曲线.经过研究,对于抛物线有如下的结论:
结论3如图3,已知抛物线y2=2px,F(x0,0)是x轴上一定点,直线l:x=x0-p是相应于定点F的定直线,T为直线l上任意一点,过定点F作TF的垂线交抛物线于P、Q两点,则过点T且与y轴垂直的直线平分线段PQ.

图3
证明:设T(x0-p,t),
(1)若t=0,则线段PQ的中点即为F,结论显然成立.

综合(1)、(2)可得结论成立.
在解决一个问题后,思考此问题相应的逆命题是否成立.通过探究可以得出如下结论.
证明:因为M与定点F不重合,所以弦PQ所在直线的斜率存在且不为零(因x0≠0).
设PQ:y=k(x-x0)(k≠0),
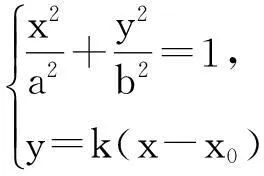
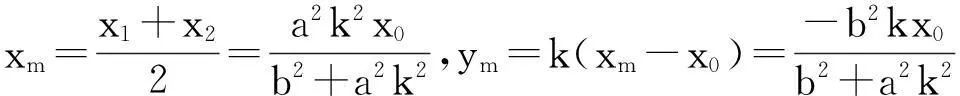
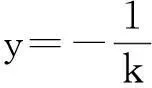
结论6设M是抛物线y2=2px的过定点F(x0,0)的弦PQ的中点,且M与定点F不重合,则过M和y轴垂直的直线与过点F垂直于弦PQ的直线的交点落在定直线l:x=x0-p上.
结论5和结论6的证明过程与结论4的证明过程类似,在此不再再赘述.
(注:本文得到朱保仓老师指导,特此致谢!)

