S变换熵理论及其在电力系统故障检测中的应用研究

陶维青，夏　熠，陆鼎堃（合肥工业大学电气与自动化工程学院，安徽合肥　230009）



S变换熵理论及其在电力系统故障检测中的应用研究

陶维青，夏熠，陆鼎堃
（合肥工业大学电气与自动化工程学院，安徽合肥230009）

摘要：S变换作为新兴的信号处理方法，在电力系统中得到越来越广泛的应用。信号经S变换处理后数据众多，有效地利用该数据并从中挖掘和提取出相应的特征量来检测电力系统故障或判别其稳定性至关重要。文章利用S变换具有的高分辨率时频特性和信息熵对系统状态进行表征，将两者相结合来定义S变换奇异熵和S变换能量熵，并给出其算法，揭示了2种S变换熵对系统故障的表征机理。对理论信号和基于PSCAD/EMTDC软件仿真的电力线路故障信号的分析表明，2种S变换熵对系统变化敏感度高，且不受噪声干扰，能够有效地检测出电力系统故障。

关键词：电力系统；S变换熵；故障检测

0　引　言

现代电力系统越来越进入大规模与智能化的时代，人们在享受着大电网所带来的巨大利益的同时，不能忽略其潜在的危险，局部电网的某些问题可能诱发恶性连锁反应，最终酿成大面积停电的系统事故［1］。因此，及时检测电力系统的各种故障，准确快速地分类故障，建立一套高效的电力系统故障信息在线检测与分类系统，对于电力系统故障诊断及预防都是十分重要的。

随着智能电力自动化设备的发展，准确、实时地获取电力系统各种故障实时信息成为现实，有关利用这些信息数据实现故障信息的特征提取与分类，国内外研究者已做了大量的研究工作。文献［2］将熵的概念引入电力系统中，预见性地提出熵原理在未来电力系统研究中必将具有极大的应用潜力。小波变换分析的引入，在电力系统暂态信号分析领域发挥了重要作用［3-4］。文献［5］将小波分析技术与信息熵理论相结合，用于医学上对脑电波信号的分析研究，取得了较好的效果。文献［6-7］将小波熵理论引入电力系统信号分析与故障特征提取，开拓了电力系统故障诊断新思路。随后，众多研究者对于小波熵理论在电力系统中的应用已进行深入研究，并取得了一定的成果，如高压线路故障选相［8］、自适应重合闸［9］及暂态保护［10-11］等。

S变换作为新兴的信号处理方法，其在电力系统中的应用效果得到了广大研究者的认可。文献［12］选取故障后各馈线零序电流的短窗数据，利用S变换对于频率的高分辨率来确定配网故障零序电流的主导特征频率，并比较该主导特征频率上各馈线零序电流的S变换能量来实现故障选线。文献［13］采用S变换提取信号的幅频特性与相频特性，利用各频率点的模值和相角信息，制定一系列投票规则，定义投票信心度。通过对多个采样点的投票机制，形成投票统计图，最终实现故障选线。文献［14］提出了一种新的电压闪变计算方法，利用S变换的“幅值-时间”与“频率-时间”信息来追踪闪变过程，能够揭示出电压在每个频率上的闪变过程，能够迅速、准确地识别闪变元件，取得了很好的效果。

本文将S变换理论和信息熵原理相结合，充分利用各自优点，给出了2种S变换熵的定义及其计算方法，并对概念及其机理进行了研究，旨在提出一种新的特征提取方法，探讨S变换熵在电力系统故障检测领域应用的可能性。

1　S变换与Shannon信息熵

1.1S变换

S变换［15］是连续小波变换（以Morlet小波为基本小波）的扩展。通过S变换可以将信号通过三维时频矩阵清晰地表达结果。与连续小波变换相比，S变换在高频段的分辨率更高更细致，变换结果直观且易于理解；与短时傅里叶变换相比，S变换窗口宽度及高度随频率的变化，而短时傅里叶变换是固定的。

定义信号h（t）的S变换为：

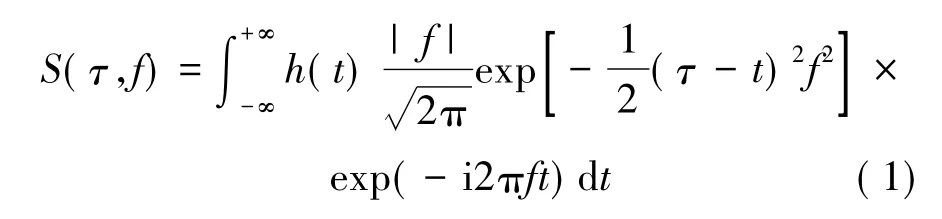
S变换频率域的表达式为：

（2）式中，f≠0，从而S变换可以实现使用快速傅式变换（fast Fourier transformation，FFT）的快速计算。S变换的离散化为：

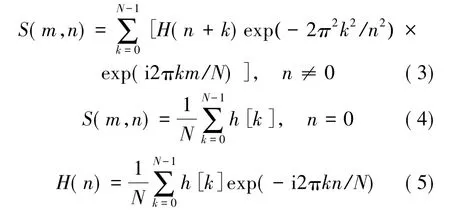
对采集到的N个离散信号点h［i］（i＝0，1，2，…，N-1）采用S变换，变换得到（n＋1）×m复时频矩阵，即为S矩阵，采样时间点以列表示，频率对应着每行。第1行为信号的直流成分，间隔的频率差和第n行的频率差分别为：

其中，N和fs分别为采样点数和频率。

S模时频矩阵是对S矩阵的元素求模后得到的，其行向量对应频率分量，列向量为采样时刻的信号幅值特性。基于S变换的过程，可以得出线性、局部性、多分辨率及无损可逆性等几个重要特征。

1.2Shannon信息熵

Shannon熵由Shannon于1948年提出，是度量分析数据不确定度的一个重要理论，其定义如下：假设一个由n个离散随机变量组成的样本空间集X＝{ x1，x2，…，xn}，其中每个状态xi对应一个概率Pi＝P（xi），有0≤Pi≤1，∑Pi＝1。状态xi的不确定信息量定义为：

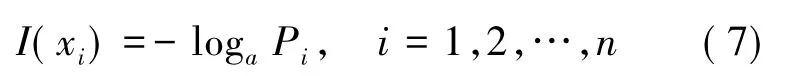
其中，对数底a决定熵的单位，当a＝2、e、10时，熵的单位分别为bit、nat、Hartley，本文选择以e作为对数底。输出I称为自信息量，无法表征整个信息源的信息度量。因此，定义自信息量的数学期望作为信息源的平均自信息量，即熵，记为H （X），其表达式为：

2　S变换熵的定义

基于现有奇异值分解、信息熵、能量熵理论，以及小波奇异熵、能量熵理论，本文将S变换与信息熵相结合，提出了基于S变换的能量熵、奇异熵。

2.1S变换能量熵

S变换具有良好的时频局部化能力，将S变换后得到的模时频矩阵处理成一个概率分布序列，由这些模值计算得到的熵值反映了该模值矩阵的稀疏程度，即信号概率分布的有序程度。假设给定一个离散信号x含有n个采样点数。S能量熵的求解步骤如下：

（1）信号x经S变换得到一个复时频矩阵，记为S矩阵。将S矩阵各个元素求模，得到一个新的矩阵，记为模时频矩阵D。

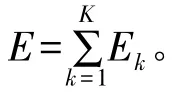
随着时间窗的滑动，可以得到S熵随时间变化的规律。（9）式中定义的S熵能反映电压或电流在时域和频域上的能量分布信息。

2.2S变换奇异熵

假设信号经S变换得到的模时频矩阵构成一个m×n的矩阵D，根据奇异值分解理论，对于矩阵D，必然存在一个m×r的矩阵U、一个r×n矩阵V和一个r×r矩阵Λ，使得矩阵D分解为：

其中，Λ为对角线矩阵，其主对角线元素λi（i＝1，2，…，r）是非负的，且按降序排列。这些对角线元素即为时频模矩阵D的奇异值。为了定量描述信号的频率成分及分布特征，定义S奇异熵SSE为：

参照信号的奇异分解理论，S奇异熵直接反映了被分析信号在时频空间中能量分布的不确定性。信号越简单，能量越集中，S奇异熵越小；信号越复杂，能量越分散，S奇异熵越大。故S奇异熵能够在宏观上衡量信号的复杂程度。

3　故障检测分析

3.12种S熵对故障揭示原理分析

对于信号的变化可分为动态幅值上的变换和频率上的变化。

（1）信号幅值变化，频率固定。假设给定信号S1（t）如下：

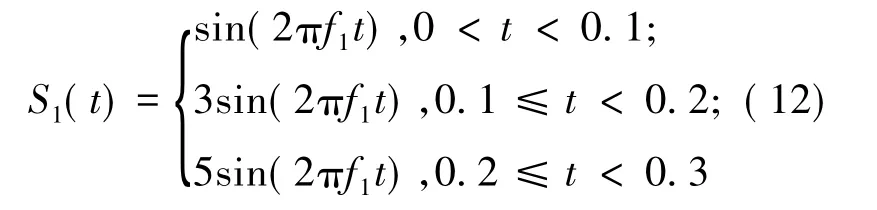
其中，频率f1＝50 Hz，保持不变，幅值变化。设置采样频率为4 kHz，并设置一个长度为10个采样点的滑动时间窗，时间窗的滑动步长为10个采样点，根据SEE和SSE的定义，可以计算得到S（t）在不同分解尺度下S变换奇异熵和能量熵。所谓分解尺度是指当信号被S变换后形成模时频矩阵，对不同频段进行划分，分解尺度越高则划分越细，整合后矩阵行数越多，分析效果越明显；反之，分解尺度越低则矩阵行数越少，分析效果可能会受到不同程度的影响。

本文采用L（低分解度）、M（中分解度）、H（高分解度）3种分解尺度，其中高低是相对而言的，分别相应得到信号的S变换能量熵（SLEE、SMEE、SHEE）以及S变换奇异熵（SLSE、SMSE、SHSE）值。所得结果如图1所示。

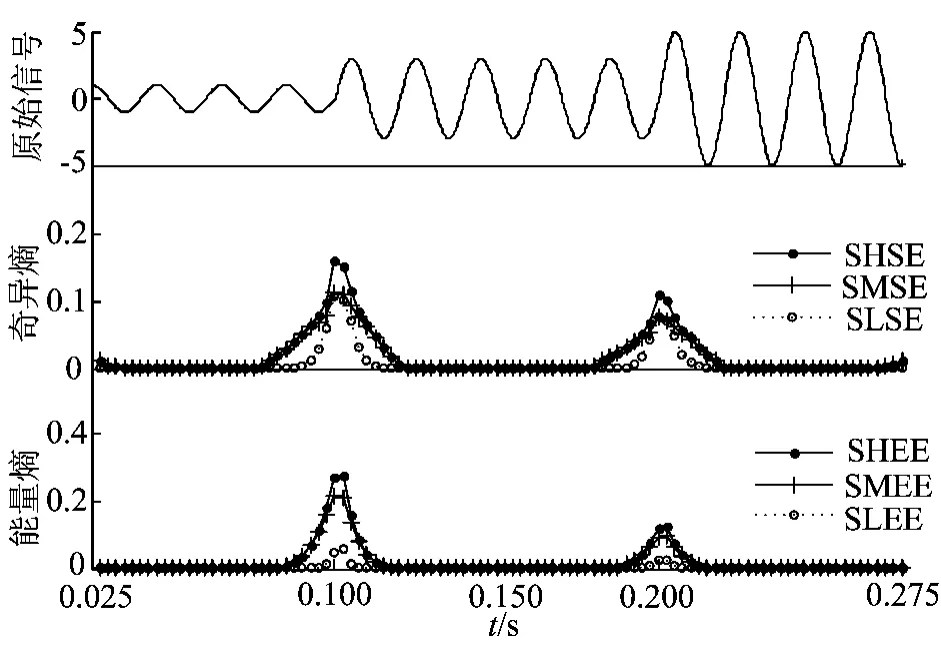
图1　幅变系统下2种S-熵变化规律

由1可以看出，2种小波熵在暂态幅值突变过程中均增大，而在信号稳态时，2种小波熵值均很小。由此可以判定小波熵检测信号幅值突变具有较好的能力，且熵值的大小与信号幅值大小无关。同时，熵值的大小与最大分解尺度具有一定的相关性。对于能量熵来说，当信号所含频率成分固定时，在一定范围内分解尺度越大，能量熵值越大，其检测突变暂态过程越明显。

（2）信号频率变化，幅值固定。假设给定信号S2（t）如下：

其中，fi＝50＋（i-1）×200。

按照该方法，设置采样频率为4 kHz，设置一个长度为10个采样点的时间窗，将时间窗以10个采样点为步长沿时间轴滑动，按低、中、高3种尺度分解，结果如图2所示。

图2　频变系统下2种S变换熵变化规律

由图2可以看出，2种S变换熵在暂态幅值、频率突变过程中均显著增大，而在信号稳态时，2 种S变换熵值均很平稳。由此可以判定S变换熵在检测信号突变中具有较好的能力，同时在一定范围内，分解尺度越大，检测暂态突变过程越明显。

3.2输电线路故障检测分析

由以上分析可看出，S变换熵对动态系统参数的变化或信号频率分布的改变具有独特的敏感性。在电力系统中，当电网或电力设备发生故障时，其系统参数将发生改变，相应的电流、电压、功率等将发生变化，出现暂态变化并逐渐过渡到稳态。另一方面，以基波为主的电流、电压信号将突变为以基波为主，并叠加一系列高次谐波和较宽频带的暂态分量。基于以上分析，S变换熵对电力系统故障具有良好的检测能力。

以一条10 kV的输电线路为例，线路总长为5 km。在工频情况下，正序参数R1＝0.45 Ω/km、L1＝0.933 7 mH/km、C1＝0.070 7 μF/km，零序参数R0＝0.72 Ω/km、L0＝4.126 4 mH/km、C0＝0.047 8 μF/km。本文建立PSCAD/EMTDC仿真模型，分析线路在3.5 km处发生两相接地短路故障，选取采样频率4 kHz，得到故障前后的三相电流IA、IB、IC和零序暂态电流I0。简化线路如图3所示。

图3　简化10 kV线路模型

采用较高分解尺度，在0.2 s时刻处发生AB两相金属性短路接地故障，仿真获取故障时刻前4个周期与后4个周期的三相电流电压及零序电流数据，分别求取其S奇异熵和S能量熵，结果如图4～图6所示。

图4～图6以线路发生AB两相短路故障时的电流、电压及零序电流为研究对象，仿真发现2 种S变换熵均在故障发生时显著增加，由此可作为判断故障发生的特征量，且具有极好的故障时刻定位能力。

经分析发现，故障发生后，无论是相电流、相电压还是零序电流，其S变换熵均在0～1之间显著增大，与其他故障检测特征量相比，其显著特点是不受被分析电流、电压幅值的影响。

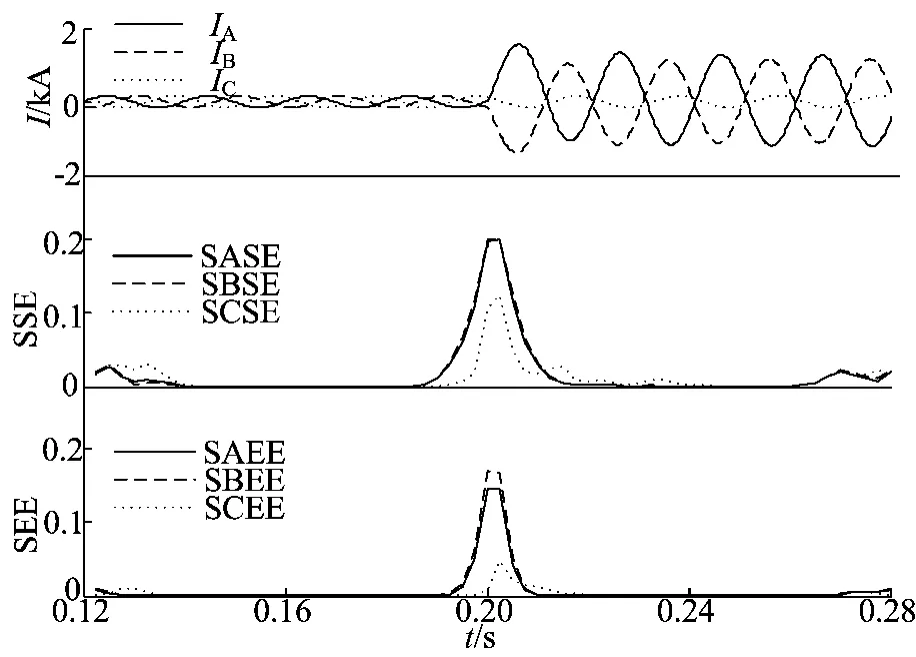
图4　AB两相接地故障三相电流及其SSE和SEE

图5　AB两相接地故障三相电压及其SSE和SEE

图6　AB两相接地故障零序电流I0及其SSE和SEE

3.3S变换熵抗噪声能力分析

由于S变换作为时频域的一种信号处理方法，其本身具有一定的去噪能力，为了探讨S变换熵的抗噪声能力，同样采用图3的配网仿真模型，中性点经消弧线圈接地，进行A相单相金属性接地故障仿真，故障时间为0.15 s，获取故障相电流及零序电流数据，并加入一定的高斯白噪声，信噪比为SNR＝25，分别求取其S变换奇异熵与能量熵，结果如图7、图8所示。

图7　A相接地短路故障加噪的IA及其SSE和SEE

图8　A相接地短路故障加噪零序的I0及其SSE和SEE

分析发现，2种S变换熵均有一定的抗噪声能力，均可以在故障发生时准确体现出电流的突变，说明S变换熵对噪声干扰不敏感，因此，S变换熵在电力系统故障检测中具有较好的实际应用价值。

3.4S变换熵对单相高阻接地故障的识别

在中性点非有效性接地的配电网系统中，单相高阻接地故障的识别一直以来都是电力系统研究中的一大难题，由于接地电阻较大，故障电流小，电压降小，三相电流几乎对称，无明显的过流现象，也不影响负荷正常工作，故增加了高阻接地检测的难度［16-22］。为了探讨S变换熵对高阻接地故障的识别能力，进行了A相经高阻接地故障的仿真，配网模型采用中性点不接地系统，接地电阻为1 000 Ω，故障时刻为0.15 s，结果如图9所示。

图9　A相高阻接地短路故障时三相电流及其SSE、SEE

经过分析，S变换熵对于高阻接地故障仍有较好的识别效果，故障相A相的SSE和SEE的幅值均发生突变，且幅度明显高于其他两相。这说明S变换熵对于故障发生时的微小暂态扰动有较精确的识别和分辨能力。

总体来说，2种S变换熵都能够准确检测线路故障，指示故障时刻，具有较好的实时性，是输电线路故障检测的一种新颖的方法，对于电力系统故障检测具有一定的实用价值。基于2种S变换熵对电力系统暂态信号的分析机理、暂态信号分类方法还有待于进一步研究。

4　结束语

本文结合S变换理论和Shannon信息熵定义，提出了基于S变换奇异熵和能量熵2种S变换熵的概念，并给出了其计算方法，验证了S变换熵对系统信号特征提取的机理，仿真分析了2种S变换熵对2种理论信号变化的特征识别能力。

本文研究了S变换熵对电力系统暂态信号特征提取的机理，应用2种S变换熵对线路常见故障信号进行了仿真分析，分析表明，2种S变换熵均能很好地检测线路故障，对噪声敏感程度低，且对微弱暂态过程有着较强的识别能力，具有计算简单、实时性好的特点，在电力系统故障检测领域具有较好的应用前景。

［参考文献］

［1］杨卫东.熵原理在电力系统中的应用前景［J］.电工技术，2000，21（4）：4-6.

［2］李志民，李卫星，李勃龙.熵原理及其在电力系统可靠性中的应用［J］.电力系统及其自动化学报，2001，13（3）：37-39，53.

［3］牛敬芳，肖本贤.基于GHM多小波和神经网络的小电流接地故障选线［J］.合肥工业大学学报：自然科学版，2014，37 （2）：159-163.

［4］陈祥训.采用小波技术的几种电能质量扰动的测量与分类方法［J］.中国电机工程学报，2002，22（10）：1-6.

［5］Rosso O A，Blanco S，Yordanova J，et al.Wavelet entropy：a new tool for analysis of short duration brain electrical signals ［J］.Journal of Neuroscience Methods，2001，105（1）：65-75.

［6］何正友，刘志刚，钱清泉.小波熵理论及其在电力系统中应用的可行性探讨［J］.电网技术，2004，28（21）：17-21.

［7］何正友，蔡玉梅，钱清泉.小波熵理论及其在电力系统故障检测中的应用研究［J］.中国电机工程学报，2005，25（5）：38-43.

［8］何正友符玲麦瑞坤等小波奇异熵及其在高压输电线路故障选相中的应用［J］.中国电机工程学报，2007，27（1）：31-36.

［9］张园园，龚庆武，陈道君，等.基于小波包能量熵判别的高压输电线路单相自适应重合闸［J］.电力自动化设备，2009，29 （9）：11-16.

［10］刘青，王增平，郑振华.小波奇异熵在线路暂态保护和全线相继速动保护中的应用［J］.电力系统自动化，2009，33 （22）：79-83.

［11］陈继开，周志宇，李浩昱.快速小波熵输电系统暂态信号特征提取研究［J］.电工技术学报，2012，27（12）：219-225.

［12］束洪春，彭仕欣.基于短窗数据S变换能量的缆-线混合配电网络故障选线方法［J］.电工技术学报，2009，24（10）：152-159.

［13］张钧，何正友，贾勇.基于S变换的故障选线新方法［J］.中国电机工程学报，2011，31（10）：109-115.

［14］Eghtedarpour N，Farjah E，Khayatian A.Effective voltage flicker calculation based on multiresolution S-transform［J］.IEEE Transactions on Power Delivery，2012，27（2）：521 -530.

［15］Stockwell R G，Mansinha L，Lowe R P.Localization of the complex spectrum：the S-transform［J］.IEEE Transactions on Signal Processing，1996，44（4）：998-1001.

［16］葛乃成，刘艳敏，倪腊琴.电力系统高阻接地故障保护综述［J］.华东电力，2011，39（5）：753-756.

［17］许庆强，许扬，周栋骥，等.小电阻接地配电网线路保护单相高阻接地分析［J］.电力系统自动化，2010，34（9）：91-94.

［18］耿建昭，王宾，董新洲，等.中性点有效接地配电网高阻接地故障特征分析及检测［J］.电力系统自动化，2013，37 （16）：85-91.

［19］高鹏，马宏忠，张惠峰，等.分接开关振动信号EMD熵和小波熵的比较［J］.电力系统及其自动化学报，2012，24 （4）：48-53.

［20］杜林，戴斌，陆国俊，等.基于S变换局部奇异值分解的过电压特征提取［J］.电工技术学报，2010，25（12）：147-153.

［21］赵妍，高磊，王永，等.基于S变换奇异值能量熵的单相自适应重合闸故障符号识别法［J］.电网技术，2010，34（12）：209-213.

［22］Moukadem A，Dieterlen A，Brandt C.Shannon entropy based on the S-transform spectrogram applied on the classification of heart sounds［C］//2013 IEEE International Conference on A-coustics，Speech and Signal Processing（ICASSP）.IEEE，2013：704-708.

（责任编辑闫杏丽）

Study of S-transform entropy theory and its application in fault detection of electric power system

TAO Wei-qing，XIA Yi，LU Ding-kun

（School of Electric Engineering and Automation，Hefei University of Technology，Hefei 230009，China）

Abstract：As a new method of signal processing，S-transform has been increasingly used in power system.The S-transform result data are abundant，and how to make good use of these data and extracted feature quantities to detect system fault and stability is essential.Combining S-transform analysis with entropy theory by exploiting the high resolution ability of time-frequency characteristics of S-transform and the ability of entropy to indicate system state，two S-transform entropy concepts，i.e.S-transform singularity entropy（SSE）and S-transform energy entropy（SEE）are defined，and the corresponding algorithms are put forward.The mechanism that these two kinds of S-transform entropy can represent system fault is revealed.The simulation results of theoretical signals and power line fault signal based on PSCAD/EMTDC simulation show that the two kinds of S-transform entropy are highly sensitive to system changes，and they can eliminate the disturbance of noise and be effectively applied to fault detection of power system.

Key words：power system；S-transform entropy；fault detection

作者简介：陶维青（1964-），男，安徽六安人，合肥工业大学副教授，硕士生导师.

基金项目：国家863高技术研究发展计划资助项目（2011AA05A107）

收稿日期：2014-12-02；修回日期：2015-03-02

Doi：10.3969/j.issn.1003-5060.2016.01.008

中图分类号：TM712

文献标识码：A

文章编号：1003-5060（2016）01-0040-06