叉车底盘神经网络逆系统解耦控制

夏　光，唐希雯，胡金芳，赵林峰（.合肥工业大学汽车工程技术研究院，安徽合肥　30009；.电子工程学院雷抗系，安徽合肥　30037）



叉车底盘神经网络逆系统解耦控制

夏光1，唐希雯2，胡金芳1，赵林峰1
（1.合肥工业大学汽车工程技术研究院，安徽合肥230009；2.电子工程学院雷抗系，安徽合肥230037）

摘要：针对叉车底盘各子系统间的干涉和耦合特性，文章利用非线性系统的神经网络逆系统方法进行叉车主动后轮转向（active rear steering，ARS）与直接横摆力矩控制（direct yaw moment control，DYC）的解耦控制。在分析底盘系统可逆性的基础上，确定解耦变量配对关系，建立BP神经网络逆系统模型并串联到原底盘系统前，使叉车底盘系统解耦成2个独立的伪线性系统；设计PD闭环控制器并与神经网络逆系统组成复合控制器，并进行仿真验证。仿真结果表明，神经网络逆系统解耦控制策略能够消除底盘各子系统间的干涉和耦合，提升叉车的状态跟踪和操纵稳定性。

关键词：叉车底盘；主动后轮转向；直接横摆力矩控制；解耦控制；神经网络逆系统

近年来，对车辆底盘各子系统进行集成控制以发掘子系统功能潜力成为车辆动力学的一个研究热点［1-2］。随着汽车上电控系统的成熟应用，工程车辆的主动安全也逐步成为研究的热点，目前，占叉车总产量75%以上的平衡重式叉车由于行驶工况复杂、工作环境恶劣、侧翻事故高发，也开始装备主动转向和主动制动系统来提升叉车的主动安全性［3］。

车辆底盘各子系统以实现某些局部功能为目标，如主动后轮转向（active rear steering，ARS）和直接横摆力矩控制（direct yaw moment control，DYC）均能提升车辆的侧向稳定性［4-5］，但存在控制功能的交叉，也不可避免地存在干涉耦合作用，使整车系统功能下降、可靠性降低。若设计控制系统时，能对各通道相互耦合的底盘集成系统进行解耦，切断对象各回路间的耦合联系，使之转化为若干个单输入、单输出系统，消除动力学子系统间的相互作用，则可发挥出各独立子系统不能提供的额外功用，提升车辆的综合性能。文献［6］采用多变量频域控制方法消除了主动前轮转向系统（AFS）和电子稳定系统（ESC）间的干涉和耦合；文献［7］采用非线性解耦控制理论设计解耦控制器，消除了主动悬架（ASS）和电动助力转向（EPS）间的耦合及路面不平度干扰对整车性能的影响；文献［8］通过抑制底盘其他控制输入的影响来实现控制目标，实现了四轮转向（4WS）、车辆动力学控制（VDC）和ASS间的解耦；文献［9］通过拟线性的方法重构了车辆3自由度仿射非线性模型，应用解耦控制方法实现了该3自由度非线性系统的解耦。

本文主要针对轮胎非线性特性导致的车辆非线性动力学特性，利用非线性系统的神经网络逆系统方法［10］进行叉车ARS与DYC的解耦控制，并利用Matlab/Simulink对控制系统进行仿真分析，验证底盘系统的解耦控制效果。

1　控制系统参考模型

本文所研究的叉车底盘系统基本上没有传统汽车底盘系统中的悬架系统和橡胶衬套连接副，因而轮胎的非线性特性是导致叉车整车非线性动力学特性的主要因素，且平衡重式叉车为“后轮转向＋前轮驱动”的底盘布置模式，所以本文主要考虑轮胎的非线性特性进行叉车底盘ARS与DYC的解耦控制，故采用具有侧向和横摆2个自由度的非线性车辆模型。

控制系统参考模型为非线性2自由度动力学模型，ARS与DYC分别从侧向和纵向对整车的横摆和操纵稳定性进行控制，采用包含侧向和横摆2自由度的车辆模型作为两者共用的控制参考模型，如图1所示。控制系统是一个由前后4个非线性特性轮胎支撑于地面的、具有侧向和横摆2自由度运动的车辆模型，该模型能够反映驾驶员的转向输入和车辆质心侧偏角与横摆角速度之间的非线性关系。

图1中，v、β和ωr分别为车辆的纵向速度、质心侧偏角和横摆角速度；m为整车质量；a、b分别为前、后轴距；Iz为横摆转动惯量；Caf、Car分别为前、后轮侧偏刚度；δr、δc和T分别为驾驶员施加的后轮转角、后轮转向补偿角和横摆控制力矩。

图1　控制系统参考模型

定义系统的状态变量x＝（β ωr）T，控制输入变量为u＝（δcT）T，控制输出变量为y＝（β ωr）T，车辆系统的状态方程可描述为：

显然，得到的车辆系统参考模型（1）式是一个典型的2输入、2输出的多变量系统，由于轮胎的耦合和运动关系的耦合作用，导致底盘各子系统存在相互作用，轮胎的纵向力和侧向力之间存在彼此关联，车辆的质心侧偏角和横摆角速度通过轮胎力作用产生耦合，车辆的横摆和侧向运动之间也存在耦合，因此ARS和DYC之间存在较强的耦合作用，2个控制回路之间具有较强的关联性。

为了使多变量集成控制系统的设计得以简化，需要对以上2个控制回路相互耦合的车辆多变量集成系统进行解耦。

2　解耦控制系统设计

2.1系统的可逆性分析

对（1）式状态方程描述的多输入、多输出底盘集成控制系统，其可逆性证明一般采用Interactor算法［10］，即计算输出变量y对时间的各阶导数，直到输出的导数方程中显含输入变量u，由（1）式可得：

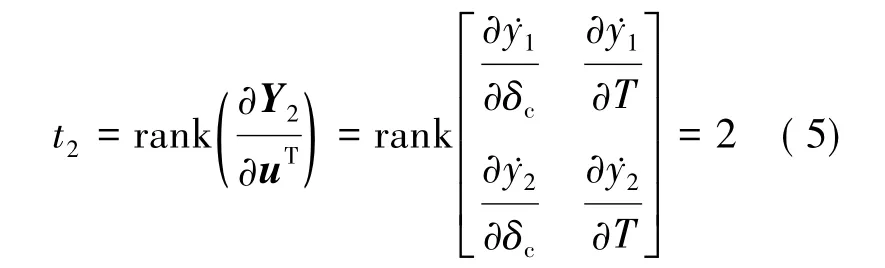
由于存在非负整数α1＝1，α2＝1，使得t2等于系统（1）式输出的个数，则系统的向量相对阶为：

由（7）式可以看出，将逆系统串联在原系统（1）式前组成的伪线性系统，相当于2个一阶积分线性子系统，这样对于包含ARS和DYC的强耦合多变量（1）式系统的控制就转化为对2个一阶积分线性子系统的控制，即可实现系统的解耦，如图2所示。

图2　解耦后的等效结构图

2.2系统解耦变量配对关系

为确定多变量控制系统输入和输出的映射关系，采用Bristol-Shinskey方法［11］，通过计算系统的相对增益矩阵来确定系统输入后轮转角与横摆力矩对系统输出质心侧偏角与横摆角速度的对应关系。

对车辆系统分别进行以下2种单输入工况激励：①横摆力矩输入为正弦曲线，方向盘转角输入为0；②方向盘转角输入为正弦曲线，横摆力矩输入为0。测量这2种单输入工况激励下的系统响应，得到该系统稳态时的第1放大系数为：

其中，φij的静态值为系统第1放大系数。

根据第2放大系数的定义，设为1/φij，则有：

综合（8）式和（9）式，分别令Δωr＝0，Δβ≠0和Δωr≠0，Δβ＝0，可得：

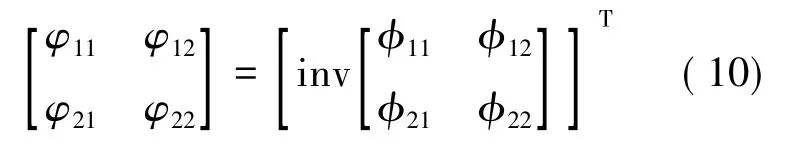
则车辆系统相对增益矩阵计算公式为：

根据相对增益矩阵的特性，当相对增益接近1时，系统可以通过这一对变量配对关系进行解耦设计，由于车辆后轮转角对质心侧偏角的相对增益和横摆力矩对横摆角速度的相对增益均在1.0～1.2之间，因而分别选择后轮转角控制质心侧偏角、横摆力矩控制横摆角速度的配对关系。

2.3神经网络逆系统的构造及训练

底盘集成系统的解析逆系统的表达式（7）式仅在原系统的参数准确、已知并保持恒定时，伪线性系统的解耦特性才能实现。为提高控制系统对参数变化的自适应能力和负载扰动的鲁棒性，应用静态神经网络和积分器来构造（7）式逆系统。

图3　逆系统BP神经网络结构

设定车速为10 km/h，驾驶员施加的后轮转角为变幅值正弦曲线，对后轮转向补偿角δc和横摆控制力矩T输入的激励信号如图4所示。

图4　神经网络逆系统训练激励信号

设定横摆角速度ωr和质心侧偏角β的响应采样周期为5 ms，根据5点数值求导算法［8］计算β和ωr的一阶数值微分和，重组以上数据得到1 000组训练数据集利用Matlab神经网络工具箱中的premnmx函数对网络输入、输出数据进行归一化处理，网络仿真测试时使用的新数据利用tramnmx接受相同的预处理，最后使用函数postmnmx来还原归一化数据。利用newff函数建立BP神经网络，选取Levenberg-Marquardt算法的trainlm作为训练函数，应用train函数对建立的BP网络进行训练，设置训练次数为500，学习效率为0.05，网络目标误差为10-4，经过61次训练后，达到所要求的训练精度。

2.4闭环控制器设计

系统解耦后，（1）式集成系统转化成互不干扰的2个单输入、单输出系统，即一阶ARS子系统和一阶DYC子系统。为改善集成系统的响应品质，设计了闭环控制器与神经网络逆系统组成复合控制器对集成系统进行控制，如图5所示。

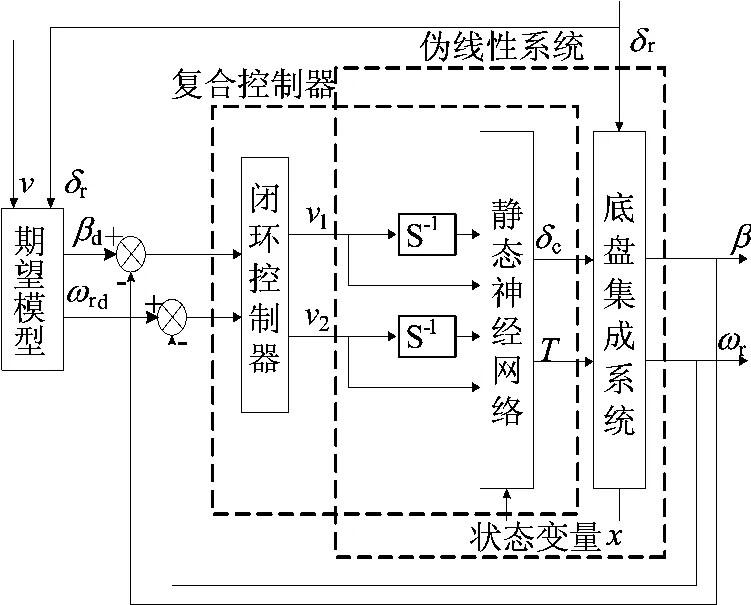
图5　底盘集成系统解耦控制结构图

解耦得到的伪线性系统的输出与输入之间具有一一对应的线性关系，可采用针对单变量线性系统理论中的PID控制、极点配置或二次型指标最优控制等方法来设计闭环控制器。在系统解耦的基础上，设计的PD闭环控制器为：

其中，e、e'为系统输出信号的偏差和偏差变化率；Kp、Kd为比例和微分系数。

另外考虑车辆的侧向力不能超过附着力，需要满足ωrd≤μg/v，其中μ为路面附着系数，因此车辆期望模型中的横摆角速度为：

车辆转向时的稳态横摆误差为：

车辆稳态侧偏角β＝-e2-ss，车辆稳态侧偏角既可以通过车速和道路半径计算得到，也可以根据稳态转角表达，将2个表达式联立可求得车辆期望模型中的质心侧偏角为：

则得到质心侧偏角和横摆角速度的期望值分别为：

3　仿真与结果分析

为验证基于神经网络逆系统方法的叉车底盘解耦控制的有效性，基于Matlab/Simulink对所设计的底盘解耦控制系统进行仿真分析。仿真车辆参数为：m＝4 639 kg；a＝1.00 m，b＝0.97 m，Iz＝8 428 kg·m2，Caf＝154.86 kN/rad，Car＝150.45 kN/rad。经反复调整，设定PD闭环控制器参数为Kp＝diag{ 16 45}，Kd＝diag{ 4.0 3.5}。设置初始车速v＝10 m/h，路面附着系数μ＝0.85，分别对没有进行系统解耦的PD控制（简称“PD控制”）和基于神经网络逆方法的解耦PD控制（简称“解耦PD控制”）进行单移线和阶跃转向2种典型工况［13］仿真，将仿真结果与理想期望值进行对比。

（1）单移线工况。设置驾驶员施加后轮转角幅值为0.08 rad、频率为0.5 Hz的单移线进行仿真，得到单移线工况下车辆的横摆角速度和质心侧偏角响应曲线如图6所示。

由图6可知，与单纯的PD控制相比，解耦PD控制的车辆横摆角速度能较好地跟踪期望值，且超调量较小，质心侧偏角也被控制在较小的范围内，利于车辆的稳定行驶。

图6　单移线工况下横摆角速度和质心侧偏角响应曲线

在单移线工况中，不同控制方式下车辆横摆角速度和质心侧偏角的峰值比较见表1所列。

表1　单移线工况仿真数据峰值比较

由表1可知，与单纯的PD控制相比，解耦PD控制下的车辆横摆角速度峰值减小了11.1%，质心侧偏角峰值减小了25.8%。

（2）阶跃转向工况。设置驾驶员施加后轮转角幅值为0.07 rad的阶跃转向进行仿真，得到阶跃转向工况下车辆的横摆角速度和质心侧偏角响应曲线如图7所示。

由图7可知，解耦PD控制可使车辆横摆角速度较好地接近期望值，且其质心侧偏角也在可控范围内。而单纯的PD控制没有考虑控制回路间的耦合影响，控制某一目标时不可避免地对其他控制目标产生不利影响，导致车辆的横摆角速度和质心侧偏角都偏离了期望值。

图7　阶跃转向工况下横摆角速度和质心侧偏角响应曲线

在阶跃转向工况中，不同控制方式下车辆横摆角速度和质心侧偏角的峰值比较见表2所列。

表2　阶跃转向工况仿真数据峰值比较

由表2可知，与单纯的PD控制相比，解耦PD控制下的车辆横摆角速度峰值减小了19.8%，质心侧偏角峰值减小了7.1%。

4　结　论

（1）采用神经网络逆系统控制方法对叉车ARS与DYC进行解耦控制，分析了集成系统的可逆性，确定了解耦变量配对关系，构造了BP神经网络逆系统。

（2）神经网络逆系统与集成系统串联得到输入输出一一对应的伪线性系统，使具有强耦合特性的叉车底盘系统解耦成2个独立的伪线性系统，实现了各控制回路间的解耦。

（3）仿真结果表明，基于神经网络逆系统控制方法的底盘解耦控制可有效提升车辆的状态跟踪和稳定性，改善极限工况下车辆的操纵稳定性。

［参考文献］

［1］Trachtler A.Integrated vehicle dynamics control using active brake，steering and suspension systems［J］.International Journal of Vehicle Design，2004，36（1）：1-12.

［2］Karbalaei R，Ghaffari A，Kazemi R，et al.A new intelligent strategy to integrated control of AFS/DYC based on fuzzy logic ［J］.International Journal of Mathematical，Physical and Engineering Sciences，2008，1（1）：47-52.

［3］司俊德，王国强，闫振华，等.翻车保护结构及其吸能构件设计与性能仿真［J］.农业机械学报，2010，41（8）：20-24.

［4］余卓平，赵治国，陈慧.主动前轮转向对车辆操纵稳定性能的影响［J］.中国机械工程，2005，16（7）：652-657.

［5］张思奇，张天侠，周淑文.基于横摆力矩分配的车辆稳定控制研究［J］.中国机械工程，2012，23（6）：751-754.

［6］朱冰，李幼德，赵健，等.基于多变量频域控制方法的车辆底盘集成控制［J］.农业机械学报，2010，41（1）：14-17.

［7］陈无畏，徐娟，胡芳，等.整车非线性系统的输入输出解耦及解耦比例微分控制［J］.机械工程学报，2007，43（2）：64-70.

［8］Kitajima K，Peng H.H∞control for integrated side-slip，roll and yaw controls for ground vehicles［C］//Intrnationgal Symposium on Advanced Vehicle Control，Ann Arbor，Michigan，USA，2000：22-24.

［9］Chen Changfang，Jia Yingmin.Nonlinear decoupling control of four-wheel-steering vehicles with an observer［J］.International Journal of Control，Automation，and Systems，2012，10（4）：697 -702.

［10］戴先中.多变量非线性系统的神经网络逆控制方法［M］.北京：科学出版社，2005：51-60.

［11］刘晨晖.多变量过程控制系统解耦理论［M］.北京：水力电力出版社，1984：74-90.

［12］Zhang Jinzhu，Zhang Hongtian.Vehicle stability control based on adaptive PID control with single neuron network［C］//International Asia Conference on Informatics in Control，Automation and Robotics，Wuhan，China 2010：434-437.

［13］夏光，唐希雯，汪韶杰，等.内燃平衡重叉车横向稳定性控制系统设计［J］.合肥工业大学学报：自然科学版，2014，37（4）：385-389.

（责任编辑胡亚敏）

Decoupling control of forklift truck chassis based on neural network inverse system

XIA Guang1，TANG Xi-wen2，HU Jin-fang1，ZHAO Lin-feng1

（1.Institute of Automobile Engineering Technology，Hefei University of Technology，Hefei 230009，China；2.Dept.of Radar Confrontation，Electronic Engineering Institute，Hefei 230037，China）

Abstract：In view of the interference and coupling characteristics among forklift truck chassis subsystems，the decoupling control of forklift truck active rear steering（ARS）and direct yaw moment control（DYC）is studied by using the neural network inverse method of nonlinear systems.On the basis of the analysis of the reversibility of chassis system，the paired relationship of decoupling variables is determined，and a BP neural network inverse system model is obtained and connected in series before the original chassis system，so the forklift truck chassis system is decoupled into two independent pseudolinear systems.A closed-loop PD controller is designed and combined with neural network inverse system into a compound controller，and the simulation verification is conducted.The simulation results show that the neural network inverse system decoupling control approach can eliminate the interference and coupling among chassis subsystems，improve the vehicle status tracking and handling stability performance.

Key words：forklift truck chassis；active rear steering（ARS）；direct yaw moment control（DYC）；decoupling control；neural network inverse system

作者简介：夏光（1983-），男，安徽萧县人，博士，合肥工业大学助理研究员.

基金项目：国家自然科学基金资助项目（51205101）；中央高校基本科研业务费专项资金资助项目（JZ2014HGBZ0054；2013bh2X0055）

收稿日期：2014-12-15；修回日期：2015-01-16

Doi：10.3969/j.issn.1003-5060.2016.01.003

中图分类号：U270.1

文献标识码：A

文章编号：1003-5060（2016）01-0014-06