RDWKCPSO-PCA-BPNN的汽车燃油消耗预测
姜 平,祖春胜,李晓勇(合肥工业大学机械与汽车工程学院,安徽合肥 230009)
RDWKCPSO-PCA-BPNN的汽车燃油消耗预测
姜平,祖春胜,李晓勇
(合肥工业大学机械与汽车工程学院,安徽合肥230009)
摘要:针对不同乘用车综合工况下理论百公里燃油消耗数据,文章提出了一种基于主成分分析(principal component analysis,PCA)和BP神经网络(back propagation neural network,BPNN)的燃油消耗预测模型;通过PCA方法对选取影响理论燃油消耗的24个因素进行压缩,简化模型结构,再利用BPNN算法,构建燃油消耗预测模型;由于神经网络中的权值和阈值对预测模型效果影响较大,采用基于随机动态惯性权重和Kent映射的混沌粒子群算法(RDWKCPSO)优化PCA-BPNN模型中的权值和阈值。对3种标准函数的寻优测试结果表明,RDWKCPSO优化算法更容易跳出局部最优实现全局寻优,提高了模型适应能力及预测精度。
关键词:BP神经网络;权值和阈值;混沌粒子群算法;主成分分析;燃油消耗预测;Kent映射
0 引 言
交通运输节能减排是我国三大重点领域之一,交通运输行业消耗了1/3以上的石油[1]。2011年石油进口量占据总需求量的1/2左右,并在随后2 a中逐年攀升[2];预计2020年左右石油进口率将超过70%[3]。汽车数量的不断增多导致我国对石油的需求量不断增大,故而在汽车研发过程中,汽车燃油消耗的理论预测至关重要。在燃油消耗预测的问题上,国外一些学者通过神经网络的方法,针对发动机参数、车型参数等因素建立汽车燃油消耗预测模型[4-5];而国内一些研究者通过碳平衡法计算燃油消耗[6]或者建立基于行驶工况特征的燃油消耗预测模型[7]。
BP神经网络(back propagation neural network,BPNN)中的权值和阈值通常是沿着网络误差变化的负梯度方向进行调节的,最终使网络误差达到极小值。由于梯度下降算法的固有缺陷,标准的BPNN通常具有收敛速度慢且容易陷入局部极小值的缺点[8-9],为此一些学者采用遗传算法[10](genetic algorithm,GA)、粒子群算法[11](particle swarm optimization,PSO)等群智能算法对参数进行寻优,使BP算法不依赖于梯度下降思想,从根本上克服BPNN的本质缺陷,改善模型的学习能力和预测精度。标准PSO算法在求解高维复杂地形的函数时,容易陷入局部最优或过早收敛[12],而实际应用中许多优化函数往往具有高维、多峰、地形复杂等特点,表现为全局最优点附近分布着许多局部最优点,对这类函数优化问题,PSO算法易早熟收敛到局部解,优化精度难以提高。
针对上述问题,本文提出基于随机动态惯性权重和Kent映射的混沌粒子群算法(RDWKCPSO)优化BPNN的权值和阈值,通过主成分分析(principal component analysis,PCA)将燃油消耗的影响因素压缩成的7个主成分得分变量作为模型的输入变量,综合工况下理论百公里燃油消耗量作为输出变量,利用RDWKCPSO-PCA-BPNN构建燃油消耗的预测模型。该模型具有很高的预测精度,能为汽车制造厂商提供汽车燃油消耗预测的参考。
1 理论分析
1.1BP神经网络和PSO算法
BPNN算法是人工神经网络中应用最为广泛的算法之一。在BPNN中,包含多个隐含层的网络,具备处理线性不可分问题的能力。BPNN由输入层、隐含层和输出层组成,数据从输入层经隐含层逐层向后传播,训练网络权值时,则沿着减少误差的方向从输出层经过中间各层逐层向前修正网络的连接权值,随着学习的不断进行,最终的误差越来越小[13]。
3层BPNN示意图如图1所示。
PSO算法是一种基于简单的社会模型的智能算法,可以具体描述为总数N个粒子在D维的搜索空间中飞行。其数学表示如下:设zi=(zi1,zi2,…,ziD)为第i(i=1,2,…,N)个粒子的D维位置矢量,根据事先设定的适应度函数计算zi当前的适应度,即可衡量粒子位置的优劣;vi=(vi1,vi2,…,viD)为粒子i的飞行速度;pi=(pi1,pi2,…,piD)为粒子迄今为止搜索到的最优位置;pg=(pg1,pg2,…,pgD)为整个粒子群迄今为止搜索到的最优位置。

图1 3层BPNN示意图
在每次迭代中,粒子根据(1)式更新速度和位置,即

其中,ω为惯性权重,通常取[0,4]之间的常数;c1、c2为学习因子,通常取[0,2]之间的常数;r1、r2为2个服从均匀分布的随机数,取值范围为(0,1)。
1.2RDWKCPSO算法
1.2.1随机动态惯性权重
由(1)式可知,惯性权重ω对PSO算法优化性能有很大的影响。较大的ω值,粒子飞行速度也大,粒子将以较大的步长进行全局探测,而较小的ω值在一定程度上会影响算法的全局收敛性能[14]。混沌粒子群算法(chaos particle swarm optimization,CPSO)采用线性递减惯性权重(linearly decreasing inertia weight,LDW),这种调节惯性权重的方法依赖于算法的迭代次数;在前期阶段算法的收敛速度较快,在后期的收敛速度缓慢且局部搜索能力较弱。本文采用随机动态惯性权重(random dynamic inertia weight,RDW)来达到优化目的。LDW和RDW 2种惯性权重的表达式分别为:

其中,ωmax为惯性权重最大值;ωmin为惯性权重最小值;max_gen为总的迭代次数;n为当前迭代次数;rand为(0,1)之间的随机数。
LDW和RDW 2种惯性权重随进化次数变化的对比如图2所示。

图2 LDW和RDW的对比图
1.2.2混沌映射
混沌是由确定性方程得到的具有随机性的运动状态。在一定范围内混沌变量的变化具有随机性、遍历性和规律性,利用混沌变量的这些特征优化搜索,能使算法跳出局部最优,保持群体多样性,改善算法的全局搜优性能。CPSO采用的混沌系统是Logistic映射,其表达式为:

其中,μ为混沌因子;n为迭代次数。
当μ=3.571 448时,Logistic方程开始进入混沌状态;当3.571 448<μ≤4时,该混沌方程变化周期变为无穷大,从而每次迭代方程的解都是不确定的,此时该方程成为一个混沌系统[15];故在此取μ=4,系统处于满映射混沌状态,其混沌映射的遍历性如图3a所示。而RDWKCPSO算法采用Kent映射产生混沌序列;Kent映射是一个具有代表性的、形式简单的离散混沌系统,其序列具有类随机性、遍历性以及均匀分布的特性[16],其遍历性如图3b所示,数学表达式为:

其中,a为常数,取值范围(0,1)。当a∈(0,1)和Ln∈[0,1]时,Kent映射处于混沌状态,根据文献[17],当a=0.499 7时,Kent映射产生的混沌序列最佳。


图3 Logistic映射和Kent映射的遍历性
由2种映射的遍历性对比可知,Logistic映射的均匀性较差,映射点在边缘处密度较高,这种分布不均性将直接影响整个迭代搜索的收敛速度,降低了整个算法的求解效率;而Kent映射分布均匀性较好,提高了算法优化搜索能力。
1.2.3RDWKCPSO算法流程
RDWKCPSO优化算法中将粒子群按适应值大小作递增排序,前20%的粒子进行Kent映射产生混沌序列优化,剩余80%的粒子按(3)式和(1)式更新粒子的速度和位置,反复循环迭代。RDWKCPSO的流程图如图4所示。
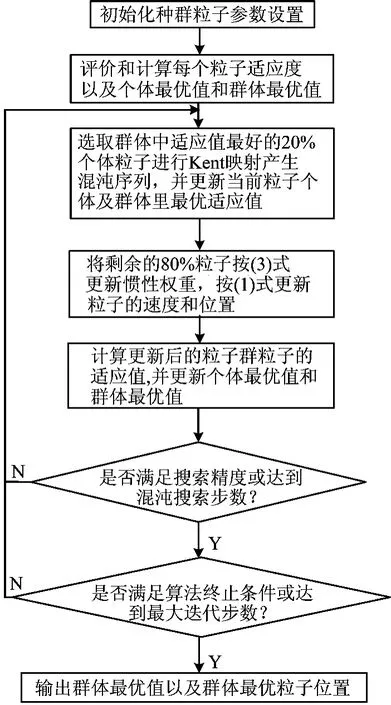
图4 RDWKCPSO流程图
2 燃油消耗预测
2.1数据采集
综合工况下百公里燃油消耗是厂家在标准工况下针对汽车怠速、匀速、加速及减速4种工况,并分别对城市道路、高速公路及郊区3种不同路况测得的百公里燃油消耗,取其平均值即为综合工况下百公里燃油消耗量。通过实验和数据采集(工业和信息化部中国汽车燃料消耗量网站)共收集包含综合工况下理论百公里燃油消耗Qs和24个参数变量的130组数据,涵盖了国产、合资及进口车型共20个品牌。其中110组数据为训练数据,20组数据为测试数据,其燃油消耗如图5所示。
经过量化处理后的部分样本数据见表1所列。其中参数变量主要包括:①国产/合资/进口来源M;②变速器参数(档位数N、传动类型G);③整车参数(车型Cm、车长X、车宽Y、车高Z、最小离地间隙H、整车整备质量Mm、满载质量MT、空气阻力系数CD);④发动机参数(排量V、气缸数NC、压缩比ε、进气形式I、最大功率Pe及其对应的发动机转速np、最大扭矩Ttq及其对应的发动机转速ntq);⑤轮胎参数(轮胎气压Pi、载重系数Li、轮毂直径Dw、轮胎扁平率Bi、轮胎宽度Bw)。
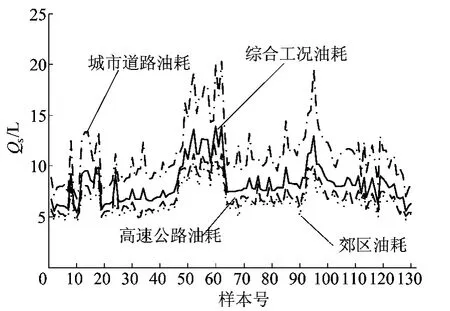
图5 样本燃油消耗数据

表1 样本数据
2.2主成分分析
为简化模型结构,缩短模型训练时间,将样本中的24个变量采用SPSS主成分分析(PCA),根据累计贡献率达到85%以上选取主成分的个数。其中前7个主成分得分变量见表2所列。
表2中,7个主成分累计贡献率达87.370%,作为BPNN模型的输入变量;百公里燃油消耗量作为输出变量。

表2 主成分得分变量
2.3优化算法性能分析
为了检验RDWKCPSO算法的寻优性能,本文采用3种代表性的标准测试函数Rosenbrock函数、Griewank函数和Schaffer函数,分别对线性递减惯性权重和Logistic映射的标准混沌粒子群优化算法(LDWCPSO)、随机动态惯性权重和Logistic映射的混沌粒子群优化算法(RDWCPSO)、随机动态惯性权重和Kent映射的混沌粒子群优化算法(RDWKCPSO)进行仿真对比。粒子群参数设置如下:学习因子c1=2.5,c2=2.0;惯性权重ωmax=0.9,ωmin=0.4;种群规模取50,进化次数为300;混沌搜索步数取30。每种算法对每个测试函数运算20次,取结果的平均值作为参考量,测试结果见表3所列。

表3 3种算法的平均最优值测试结果
Rosenbrock函数、Griewank函数和Schaffer函数的平均寻优曲线如图6所示。

图6 3种函数的平均寻优曲线
测试函数描述如下:
(1)f1即Rosenbrock函数,理论最优值为0。它是很复杂的函数,当其维数小于4时为1个单峰函数,其全局最优解被狭长的“山谷”所包围;当其维数大于4维时,则转变为1个多峰函数。其表达式为:
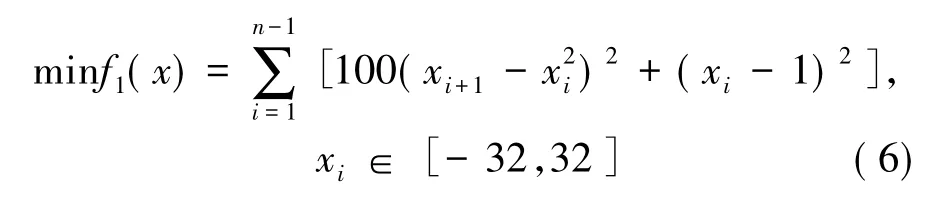
(2)f2即Griewank函数,理论最优值为0。它是多峰函数,随着维数的增加,其局部极小点的数量将减少。其表达式为:

(3)f3即Schaffer函数,理论最优值为0。它是具有强烈震荡的多峰函数。其表达式为:

由图6可知,对于多维度、多极值函数的寻优,LDWCPSO算法已不能体现出任何优越性;而RDWKCPSO算法在寻优初期保持较快的收敛速度,在粒子群进化后期寻优结果达到稳定后,更容易跳出局部最优解、实现全局寻优,提高了寻优精度。此外,由表3的的测试结果对比可知,3种函数的平均寻优值中,RDWKCPSO算法的平均寻优精度均明显高于另外2种算法。
2.4模型构建
PCA-BPNN模型中的隐含层数目是根据Komogorov定理的经验公式确定为15。由于网络模型中的权值和阈值对其预测效果影响较大,故而在构建综合工况下理论百公里燃油消耗的预测模型之前,采用寻优效果更好的RDWKCPSO算法确定PCA-BPNN模型中的权值和阈值。在参数寻优过程中设置110组训练样本的平均相对误差作为PSO算法的适应度评价标准,其适应度函数曲线如图7所示,最优适应值为0.002 4;输入层与隐含层的权值和阈值见表4所列;隐含层与输出层的权值见表5所列,阈值为-1.251 4。

图7 RDWKCPSO的适应度曲线
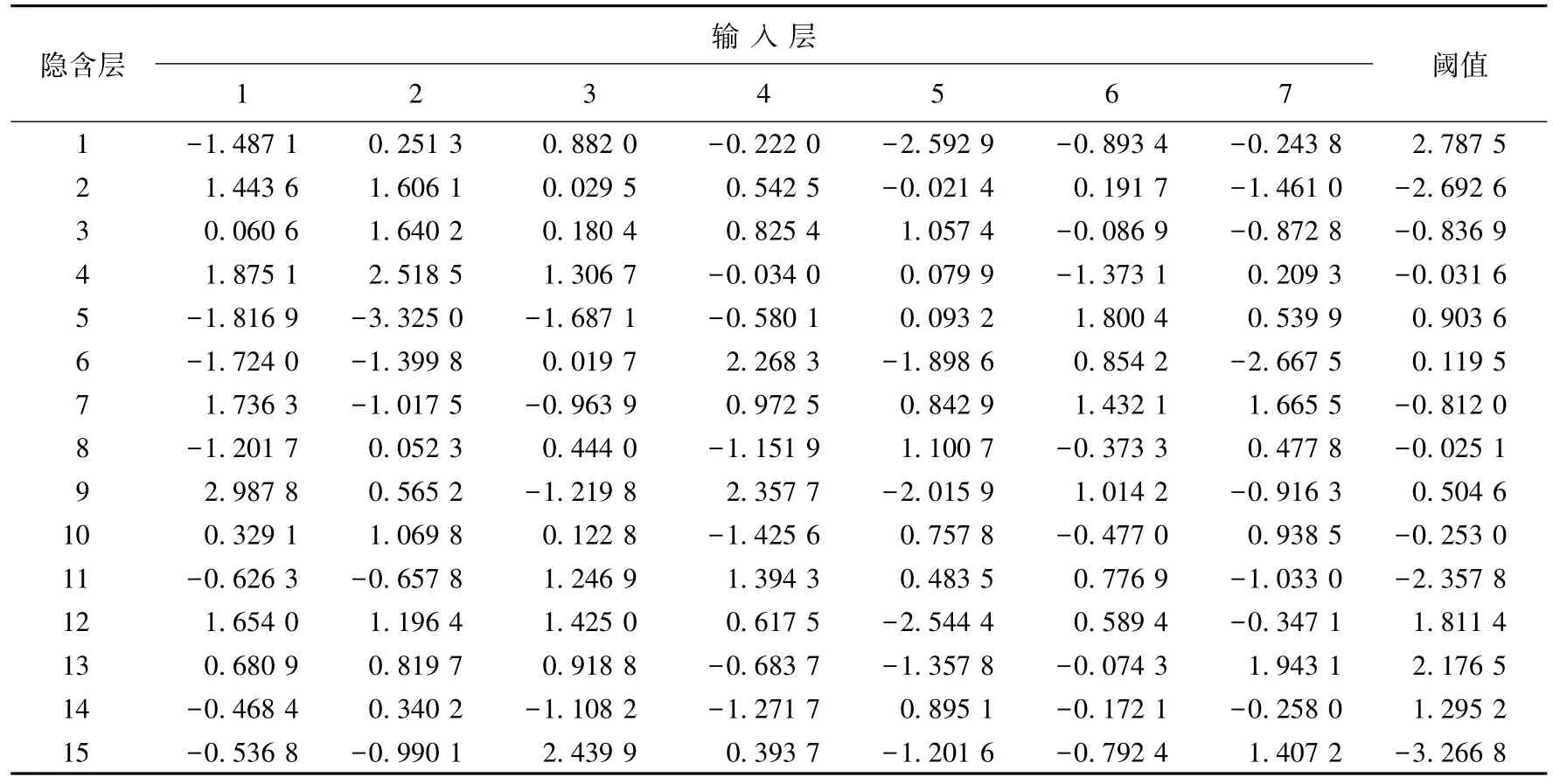
表4 输入层与隐含层的权值和阈值

表5 隐含层与输出层的权值
3 结果分析
由RDWKCPSO寻优算法确定的权值和阈值构建PCA-BPNN的百公里燃油消耗预测模型,其训练数据和测试数据的结果曲线如图8所示,20组测试样本的百公里燃油消耗原始数据与预测数据的对比结果见表6所列。

图8 样本原始数据与预测数据对比图
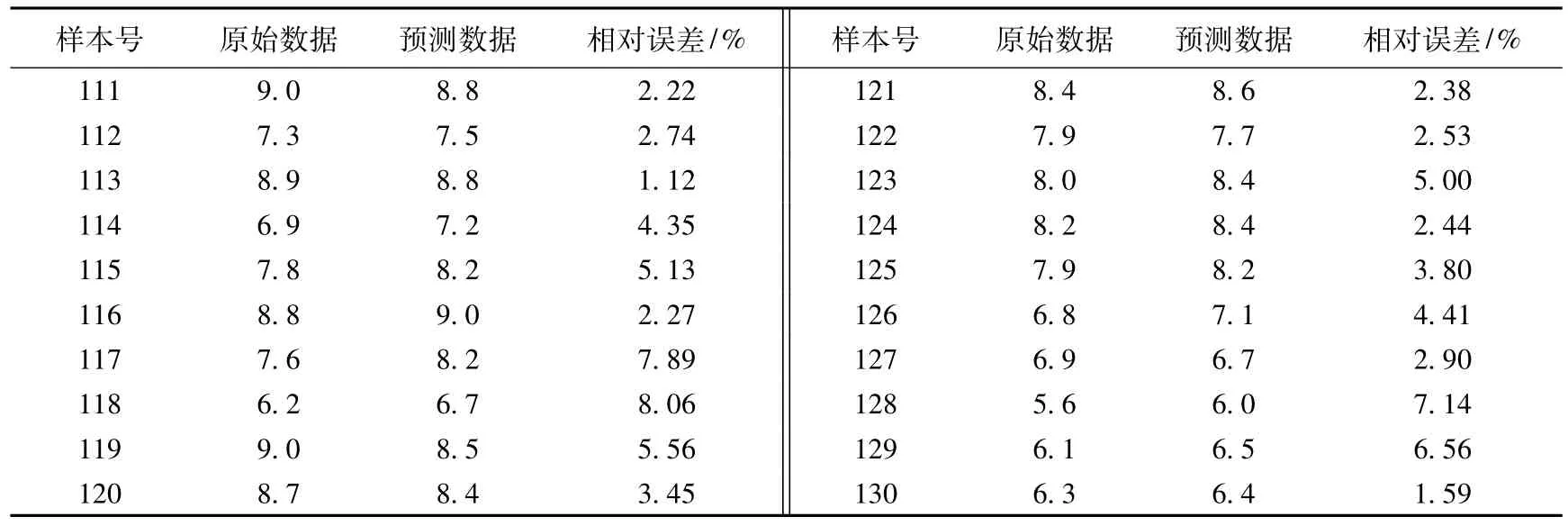
表6 测试样本百公里燃油消耗原始数据与预测数据对比 L
由图8可以看出,样本原始数据曲线与模型预测数据曲线相当接近,前110组训练样本中2条曲线几乎重合。由表6测试样本的预测结果对比可知,20组测试样本的平均相对误差为4.08%,最大相对误差为8.06%,测试样本相对误差的均方根值为4.56%,而所有样本的平均相对误差为0.83%,所有样本相对误差的均方根值为2.24%。由这些数据可以看出,RDWKCPSO算法优化的PCA-BPNN模型不仅可以精确地预测燃油消耗量,而且改善了模型的适应能力。
4 结 论
(1)本文通过3种典型的标准测试函数即Rosenbrock函数、Griewank函数和Schaffer函数,经过20次寻优的平均结果对比,得出RDWKCPSO算法比LDWCPSO和RDWCPSO算法的寻优精度平均高出1~2个数量级,更接近于函数的理论最优值;且在寻优后期,3种函数寻优曲线的对比表明了RDWKCPSO算法突破局部最优、寻找全局最优的能力比另外2种算法强。故而在PCA-BPNN模型预测过程中,选取了寻优算法能力强的RDWKCPSO算法来确定PCA-BPNN模型中的网络权值和阈值。
(2)采用RDWKCPSO算法优化的PCABPNN模型针对汽车综合工况下理论百公里燃油消耗进行预测,测试样本预测结果的平均相对误差仅为4.08%,相对误差的均方根值只有4.56%,由此可见该模型能够为汽车制造商提供一种有效、可靠的百公里燃油预测方法,减小了汽车研发的成本和时间。此外,该模型具有较高的预测精度和适应能力,因而提高了模型的实用性和可靠性。
[参考文献]
[1]Zhou Xiaohua,Huang Jian,Lv Weifeng,et al.Fuel consumption estimates based on driving pattern recognition[C]//International Conference on Green Computing,Communications and IEEE Cyber,Physical and Social Computing.IEEE,2013:496-503.
[2]杨志平.关于我国汽车节能减排的思考[J].交通世界,2014,30(5):120-121.
[3]史重九.必须高度重视汽车节能减排[J].交通与运输,2011,27(4):6-8.
[4]Wu Jianda,Liu Junching.Development of a predictive system for car fuel consumption using an artificial neural network[J].Expert Systems with Application,2011,38(5):4967-4971.
[5]Wu Jianda,Liu Junching.A forecasting system for car fuel consumption using a radial basis function neural network[J].Expert Systems with Applications,2012,39(2):1883-1888.
[6]Liu Jun,Wang Yun.Development on automobile fuel consumption intelligent and rapid testing system[C]//International Conference on Electric Information and Control Engineering.IEEE,2011:4942-4945.
[7]姜平,石琴.基于行驶工况特征的汽车燃油消耗的预测[J].汽车工程,2014,36(6):643-647.
[8]万定生,胡玉婷,任翔.带反馈输入BP神经网络的应用研究[J].计算机工程与设计,2010,31(2):398-400.
[9]韩基超.基于粒子群优化的神经网络及其集成算法研究[D].大连:大连海事大学,2011.
[10]李宏伟,杨国为,王晓艳.基于改进遗传算法的BP网络在降雨量预测中的应用[J].青岛大学学报:工程技术版,2010,25 (1):10-14.
[11]孙湘,周大为,张希望.一种混沌粒子群算法[J].计算机工程与科学,2010,32(12):85-88.
[12]韩月娇.粒子群算法的改进及其在BP神经网络中的应用[D].南昌:南昌航空大学,2013.
[13]陈明.MATLAB神经网络原理与实例精解[M].北京:清华大学出版社,2013:156-191.
[14]张丹,韩胜菊,李建,等.基于改进粒子群算法的BP算法的研究[J].计算机仿真,2011,28(2):147-150.
[15]唐新来,李春贵,王萌,等.基于混沌粒子群算法的神经网络短时交通流预测[J].计算机测量与控制,2010,18(8):1893-1895.
[16]陈增强,周茜,袁著祉.基于Kent映射的数字喷泉编解码方法研究[J].系统科学与数学,2011,31(6):731-741.
[17]张勇,单承赣.Kent混沌伪随机码的性能研究[J].合肥工业大学学报:自然科学版,2003,26(2):227-231.
(责任编辑胡亚敏)
·信息与动态·
Automobile fuel consumption prediction based on RDWKCPSO-PCA-BPNN
JIANG Ping,ZU Chun-sheng,LI Xiao-yong
(School of Machinery and Automobile Engineering,Hefei University of Technology,Hefei 230009,China)
Abstract:On the basis of the theoretical one-hundred-kilometer fuel consumption data under comprehensive conditions of different passenger car,the fuel consumption prediction model based on principal component analysis(PCA)and back propagation neural network(BPNN)is proposed.In order to simplify the model structure,the 24 factors that affect the theoretical fuel consumption are compressed by PCA,then the fuel consumption prediction model is established by using BPNN algorithm.Because the weight and threshold of neural network have a greater impact on the model prediction effect,the weight and threshold of PCA-BPNN model is optimized by applying the chaotic particle swarm optimization algorithm based on random dynamic inertia weight and Kent map(RDWKCPSO).The optimization test results of three kinds of standard function show that the RDWKCPSO optimization algorithm is more likely to jump out of local optimization to find the global optimization and the model adaptability and prediction precision are improved.
Key words:back propagation neural network(BPNN);weight and threshold;chaotic particle swarm optimization;principal component analysis(PCA);fuel consumption prediction;Kent map
作者简介:姜平(1974-),女,山东烟台人,博士,合肥工业大学副教授,硕士生导师.
基金项目:国家自然科学基金资助项目(51178158);安徽省自然科学基金资助项目(1508085ME94)
收稿日期:2014-11-28;修回日期:2015-03-06
doi:10.3969/j.issn.1003-5060.2016.01.002
中图分类号:TP301.6;U462.34
文献标识码:A
文章编号:1003-5060(2016)01-0007-07

