圆型纤维过滤流场数值计算与压降分析
李梦迪
(桂林航天工业学院 能源与建筑环境学院,广西 桂林 541004)
圆型纤维过滤流场数值计算与压降分析
李梦迪*
(桂林航天工业学院 能源与建筑环境学院,广西 桂林 541004)
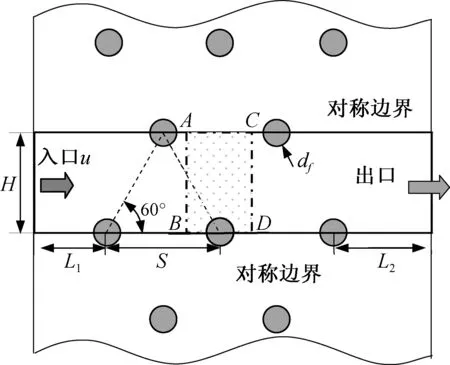
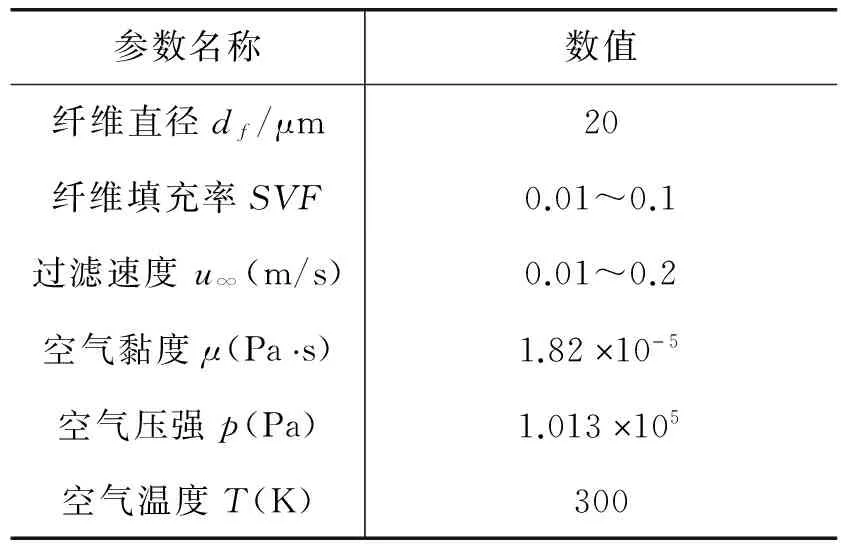
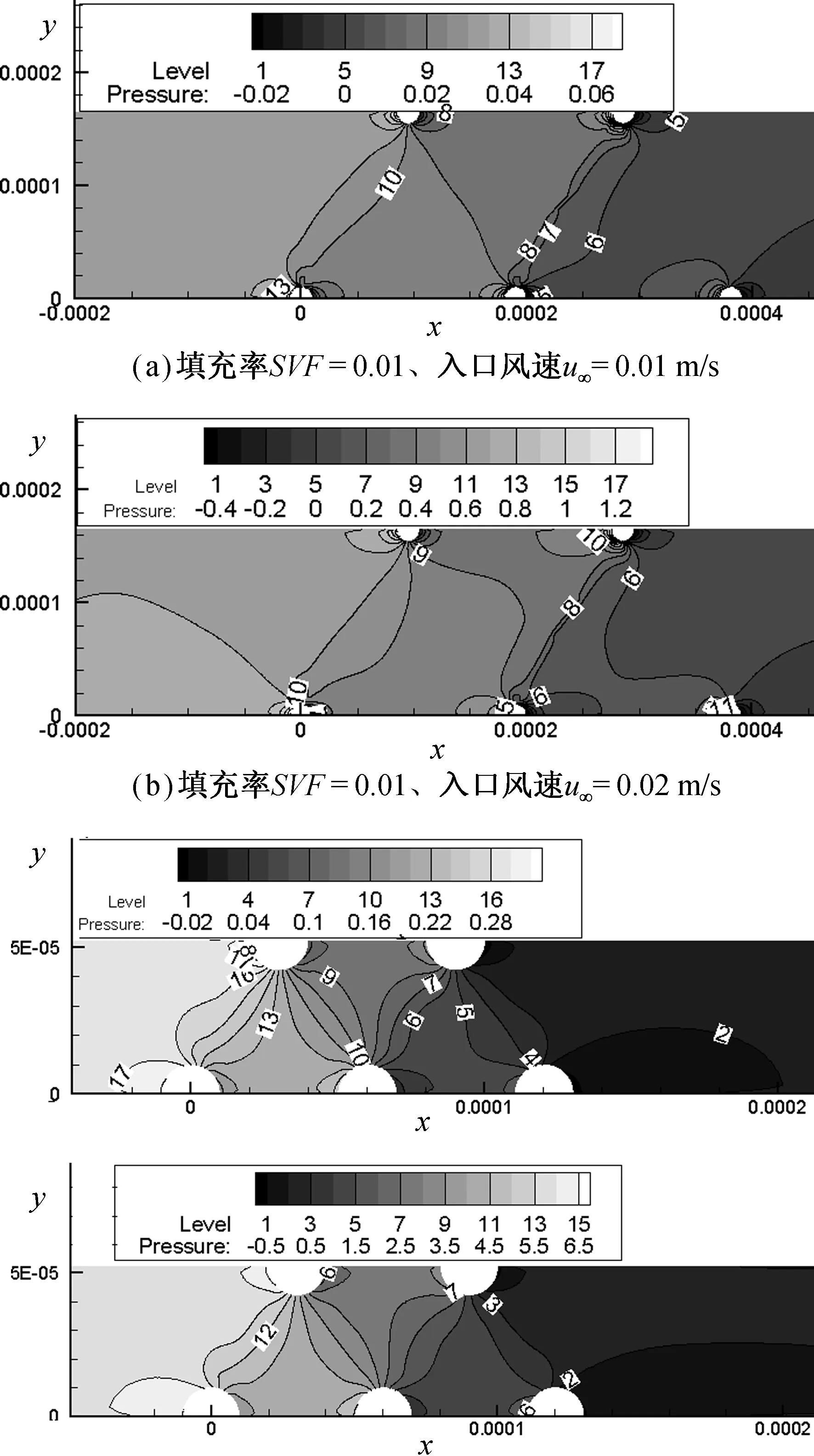
通过采用计算流体力学方法求解描述交错排列纤维模型过滤器绕流特征的Navier-Stokes方程,并计算分析了纤维附近流场分布和单纤维过滤阻力。保持纤维直径df=20 μm,重点分析过滤风速u、填充率SVF对纤维外流场分布及过滤阻力的影响。研究结果表明:当纤维直径保持不变时,单纤维稳态过滤阻力损失随过滤风速u∞、填充率SVF增大而增大;当过滤风速0.01 m/s 纤维过滤;过滤风速;填充率;过滤阻力 随着我国建筑行业、冶金矿业、火力发电等重工业的迅速发展,大量气溶胶颗粒物的排放综合导致了雾霾天气、酸雨和气候剧变等重大环境问题频繁发生[1-3]。对于小于10 μm的微粒,旋风除尘器满足不了环境保护的要求。目前,最经济也是最有效的方法之一是纤维过滤技术,该技术已广泛应用于各类工业废气净化的袋式除尘器、医院等洁净室的末端高效空气过滤器及公共建筑通风过滤器等,因此纤维过滤理论及技术的研究是一个重要研究课题[4]。从描述过滤器过滤性能的宏观模型看[5-7],对纤维上气溶胶粒子捕集过程和阻力特征的严格描述是准确估计和优化过滤器性能的前提。 显而易见,纤维过滤器的过滤效率主要取决于单纤维的颗粒捕集能力,探究单纤维的颗粒捕集机理之前必须理解单纤维外流场特性,因此单纤维过滤流场分布是研究纤维过滤理论及技术中的主要内容之一,对纤维过滤理论的发展起着至关重要的作用。已有很多文献讨论了单纤维绕流特征[8-10],Kuwabara[8]从任意排列布置的圆柱体中选取一根圆柱,求解其的二维黏性绕流流场分布,相似的结果同样由Happel[9]计算得出。从此,Kwwabara和happel关于单根二维圆柱体绕流外流场的理论求解结果就成了研究纤维过滤器的理论基础。然而,Kuwabara在求解流场时,忽略了流体的惯性作用,仅考虑了流体的粘性效应,因此,该流场仅适用于对纤维壁面附近区域粘性边界层内流场特征的描述。 针对上述现象及问题,为获得全流域流场的精确信息,从纤维过滤器中截取单纤维,本文主要模拟分析单纤维过滤,并分别与Kuwabara和Happel的理论结果进行对比验证。二维单纤维的流场求解是基于N.S.方程,采用层流模型计算单纤维绕流流场,参考了Wang[11]等提出的随机模拟方法,创建了相同纤维直径(df=20 μm)情况下不同填充率的模型。模拟分析稳态层流情况下单纤维对气溶胶颗粒的惯性捕集效率,重点分析过滤风速u、填充率SVF对纤维外流场分布及过滤阻力的影响,为纤维过滤器宏观过滤性能的预测与优化提供理论参考依据。 1.1 纤维几何模型 通过计算流体力学软件对圆型纤维过滤器进行模拟研究,如图1所示,模型是从叉排多纤维过滤器中截取的一小块对称区域,即较传统理论加入了单纤维周围环境的影响。两根纤维水平间距和竖直间距(即流域高度)分别为S和H,保持任意最近三根纤维中心连线为等边三角形,即sin(π/3)=H/S,纤维填充率SVF=πdf2/(4S×H)=(0.01、0.05、0.08、0.1),保持纤维直径df=20 μm不变,通过改变S和H(S和H相互关联)来改变填充率。为保证入口边界和出口边界处流动的充分发展,设定第一排纤维距离流体入口L1为10倍纤维直径,最后一排纤维到流体出口边界距离L2为10倍纤维直径,可保证气流在过滤器管道内充分发展。边界条件设置如下:流域入口采用速度入口(velocity-inlet);设置流域出口为压力出口(pressure-outlet);流域上下边界取对称边界(summary);纤维表面设置为无滑移壁面(wall)。并且对纤维表面进行了网格加密处理。 图1 圆型纤维数值模型 1.2 数值方法 本文考虑了相邻纤维对目标纤维流场分布的影响,并假设该纤维扰流问题稳定、不可压缩、层流,流场分布及纤维特性稳定不变,忽略热泳力等。假设沿着流动方向,流场分布呈周期变化,因此,我们可以从叉排纤维中选取一根具有代表性的单纤维进行分析,含尘气体对纤维的绕流可简化为二维情形,如图1中的区域ABCD。此外,本文研究的是低雷诺数下的纤维流动问题,流场分布完全对称,故模型上下方均可取一半纤维进行研究,以简化计算模型,节省计算时间。 对于普遍纤维过滤的情形,滤料内部流动为低雷诺数(Re<1)流动,故本文考虑的纤维绕流可视为二维不可压缩粘性定常层流流动,其连续性方程和动量方程的无量纲形式可表示为[12]: (1) (2a) (2b) 对微米级直径的纤维,其表面空气分子的滑移效应可忽略[26],故纤维表面流体满足无滑移边界条件,即 u*=0,υ*=0 (3) 应用Fluent在图1所示的区域内数值求解上述流体运动方程。在数值计算中,采用非结构网格划分计算空间域,为捕捉到纤维近壁区域精细的流场结构,对近壁区域作局部网格加密处理,经过网格独立性测试后,纤维附近最细网格为0.12m,模拟区域网格总数为40~70万。 现利用上述分析给出的数值模型,讨论相关参量对单纤维过滤阻力和惯性捕集效率的影响。如前所述,本文讨论室内环境中空气净化用纤维过滤情形,纤维填充率及过滤风速的取值范围依据通常情况下的实际运行参数选取[13-14],具体计算参数值列于表1中。 表1 数值模型计算所用主要参数 2.1 速度场分布 在所有模拟计算结果中,选择填充率SVF=0.01和SVF=0.1下两种模拟结果进行分析,即速度u∞=0.01 m/s和u∞=0.2 m/s,如图2所示,我们可以看出有一个很明显的规律:由于叉排纤维的阻碍作用,纤维间的流速大小也呈交替分布形式,纤维前后流场对称分布,速度梯度大、速度小;单纤维周围的流场受其他纤维影响出现速度极高点,两排纤维之间速度的最大值,分别出现在纤维的顶端,空气流经纤维时,纤维附近的速度越来越小,壁面处为零;在入口速度为u∞=0.01 m/s和u∞=0.2 m/s的情况下,雷诺数Re均小于1,流场为层流,且前后对称,随着入口速度的增加纤维周围的流速变化很大,流场的变化是影响粒子迹线和捕集行为的重要因素。 图2 不同填充率和过滤风速下速度云图 2.2 静压场分布 如图3所示,为分析不同填充率和过滤风速下的静压分布,本节取填充率SVF=0.01和SVF=0.1以及速度u∞=0.01 m/s和u∞=0.2 m/s四种代表性模拟结果进行分析。显而易见,叉排纤维对含尘气流有明显阻碍作用,静压场分布规律与速度场类似,呈周期性变化。此外,沿着气流流动方向,就宏观而言,流域内静压先升高,而后在纤维区域迅速降至最低,而后逐渐回升。来流绕流目标纤维时四种代表性模拟结果静压变化分别为:0.06Pa~-0.02Pa(SVF=0.01、u∞=0.01 m/s)、1.2pa~-0.4Pa(SVF=0.01、u∞=0.2 m/s)、0.28Pa~-0.02 Pa(SVF=0.1、u∞=0.01 m/s)、6.5Pa~-0.5Pa(SVF=0.1、u∞=0.2 m/s),由此可知,纤维外静压场分布受纤维填充率和过滤风速的综合影响。 图3 不同填充率和过滤风速下静压云图 2.3 纤维压力损失 Liu和Wang的研究[20]表明:对于多排纤维(叉排或顺排),气流穿过第一排纤维之后,流场呈周期性分布。然而显而易见的是,由于压力沿着流动方向逐渐降低,压力场分布不可能像流场那样呈周期性分布。单纤维的压力损失与一系列变量相关量,如空气流量Q、空气流通面积A、单纤维过滤单元长度d(如图1中虚线部分AB和CD间距,即前后压降计算面间距)、空气动力粘度μ、空气密度ρ、空气分子自由平均程λ、纤维水平间距和竖直间距S和H、纤维平均半径Rf(Rf=df/2)。尽管部分变量不是独立参数,我们仍然可以给出如下方程式: (4) 其中U代表方程。方程中的8项参数涉及三个基本量纲,白金汉定理将方程(4)整理成关于5个无量纲变量的方程: (5) 其中V代表方程。 单纤维的压力损失Δp可表述为垂直于单纤维流动方向的单位长度的阻力的表达式: (6) 其中SVF为单纤维填充率,定义如下: (7) (8) 式(8)中u∞为过滤速度。 对不可压缩流动,根据Darcy定理,当雷诺数很小时,纤维压力损失与空气流量成比例关系。然而,随着雷诺数增大到一定数值时,纤维的压力损失与空气流量之比不再是常数,而是随着空气流量增大而增大,原因在于尾波的产生以及存在附加能量的耗散。保持纤维直径不变,如图4所示,为四种不同填充率下,单纤维压力损失与速度的关系曲线,速度分布u∞=0.01-0.2 m/s,此时雷诺数Re<1,符合达西定理。当纤维直径和填充率保持不变时,单纤维压力损失随风速增大而线性增加;此外,当纤维排列方式和过滤风速保持不变时,单纤维压力损失随纤维填充率增大而增大。 图4 不同填充率下单纤维压力损失与过滤速度关系曲线 需要说明的是Kuwabara的理论解仅适用于H/S=1时的顺排和叉排圆柱体,而不是对任意排列的圆柱体都适用。事实上,Kuwabara的预测解的准确性要高于Happel的公式。此外,还需要注意的是Kuwabara和Happel的理论预测结果对顺排纤维并不十分适用,实际上,无量纲阻力应该是纤维排列结构(如顺排、叉排)、纤维填充率、H/S比值等一系列参数的综合反映,即该单纤维无量纲阻力并非无限制适用于任意排列组合的纤维结构。 图5 单纤维无量纲阻力与填充率关系验证 本文数值求解了交错平行排列模型下纤维过滤器的绕纤维流场,在此基础上保持纤维直径df=20 μm,重点分析过滤风速u、填充率SVF对纤维外流场分布及过滤阻力的影响,主要结论如下:在低Re数(Re<1)情形下,单纤维无量纲过滤阻力与Re数几乎无关,仅取决于纤维填充率SVF;采用数值模拟得到的流场计算出的单纤维无量纲过滤阻力值介于采用简化的理想粘性流场Happle模型和Kuwabara模型得到的估计值之间,在C<0.045时,数值给出的阻力估计值更接近于Happel阻力模型;当C>0.08时数值结果与Kuwabara阻力模型接近。 [1] 周敏,陈长虹,乔利平等. 2013年1月中国中东部大气重污染期间上海颗粒物的污染特征[J]. 环境科学学报, 2013, 33(11): 3118-3126. [2] 赵艳霞,侯青. 1993-2006 年中国区域酸雨变化特征及成因分析[J].气象学报, 2008, 66(6): 1032-1042. [3] 师华定,高庆先,张时煌,等. 空气污染对气候变化影响与反馈的研究评述[J].环境科学研究, 2012,25(9): 974-980. [4] 付海明,沈恒根. 纤维过滤器过滤理论的研究进展[J].中国粉体技术,2003,9(1):1008-5548. [5] Song C B, Park H S. Analytic solutions for filtration of polydisperse aerosols in fibrous filter [J]. Powder technology, 2006, 170(2): 64-70. [6] Li W, Shen S, Li H. Study and optimization of the filtration performance of multi-fiber filter [J]. Advanced Powder Technology, 2016, 2(27): 638-645. [7] Saleh A M, Tafreshi H V, Pourdeyhimi B. An analytical approach to predict pressure drop and collection efficiency of dust-load pleated filters [J]. Separation and Purification Technology, 2016, 161: 80-87. [8] Kuwabara S. The forces experienced by randomly distributed parallel circular cylinders or spheres in a viscous flow at small Reynolds numbers [J]. Journal of the physical society of Japan, 1959, 14(4): 527-532. [9] Happel J. Viscous flow relative to arrays of cylinders [J]. AIChE Journal, 1959, 5(2): 174-177. [10]Li Y, Park C W. Effective medium approximation and deposition of colloidal particles in fibrous and granular media [J]. Advances in colloid and interface science, 2000, 87(1): 1-74. [11]Wang C S, Beizaie M, Tien C. Deposition of solid particles on a collector: Formulation of a new theory[J]. Joumal of American Institute of Chemical Engineers, 1977, 23(6):879-889. [12]陈懋章. 粘性流体力学基础 [M]. 北京: 高等教育出版社, 2004: 111-112. [13]钟麟. 空气洁净技术原理[M]. 北京: 科学出版社, 2003: 125-126. [14]Tekasakul S, Suwanwong P, Otani Y, et al. Pressure drop evolution of a medium-performance fibrous filter during loading of mist aerosol particles[J]. Aerosol and Air Quality Research, 2008, 8(3): 348-365. (责任编辑 陈葵晞) 李梦迪,女,湖北荆门人。助教,硕士。研究方向:洁净燃烧技术。 杨会 TQ021; TU834; X701.2 A 2095-4859(2016)04-0476-051 模拟描述
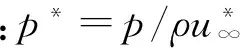
2 结果与讨论



3 结论

