倒装芯片键合头模态特性研究与实验分析

宫文峰，黄美发，张美玲

(1.桂林电子科技大学海洋信息工程学院，广西北海536000; 2.桂林电子科技大学广西先进设计与制造技术重点实验室，广西桂林541004)

倒装芯片键合头模态特性研究与实验分析

宫文峰1，黄美发2，张美玲1

(1.桂林电子科技大学海洋信息工程学院，广西北海536000; 2.桂林电子科技大学广西先进设计与制造技术重点实验室，广西桂林541004)

键合头是全自动倒装芯片键合机重要的功能运动部件，其主要功能是完成芯片的拾取、点胶和键合。键合头在高频高加速的往复多自由度运动中产生的振动和共振量直接影响芯片的键合精度，因此要求键合头应具有足够的刚度、强度和较好的动态特性。掌握键合头的模态特性及其影响因素之间的关系是自主研发高性能倒装芯片键合头的关键问题。为此，建立键合头模态特性研究系统模型，采用理论计算与实验测试相结合的方法研究键合头在安装工况下的模态特性，将ANSYS有限元仿真的结果与锤击模态试验的结果作一致性对比和分析，得到键合头准确的模态参数、刚度分布情况和影响因素。研究结果为多功能高密度芯片键合头的进一步结构优化和精度控制以及整机的防振、抑振等提供理论支撑和实验依据。

倒装芯片键合机;模态分析;锺击测试;有限元法

0 引言

倒装芯片键合机(flip chip bonder，FCB)是基于倒装焊工艺而设计的微电子后封装新设备［1－2］。它采用固晶的方式将芯片通过拾取、翻转、传送、识别、点胶和键合等过程与芯片载体固结在一起［3］。目前，我国的高性能倒装芯片键合设备基本上依赖于进口，研发具有自主知识产权的高密度倒装键合机尤为重要。

键合头是倒装芯片键合机中精度要求最高的功能运动部件之一，其主要功能是完成芯片的拾取、点胶和键合。键合头在高频高加速的多自由度往复运动中常因其结构刚度不足导致准停后而产生残余附加振动;当伺服电机或外部环境等工作频率与键合头的某阶固有频率相近或相同时将会产生共振现象［3－4］，直接影响芯片的键合精度和效率。为有效保证芯片的键合精度，有必要对键合头的动态特性和相关实验等关键技术进行研究，为自主研发高性能芯片键合头提供理论支撑和实验参考。

目前关于模态测试的研究主要集中在模态参数辨识方面［4－5］，比较有代表性的有Massa［6］提出了模糊模态分析的新概念和实验行为的预测;Kromulski J等［7］对工作变形(ODS)测定中的实验模态分析方法的应用进行了介绍;Pintelon等［8］对模态分析中的不确定性计算进行了研究;应怀樵等成功的用锤击法和变时基技术进行了铁路桥的模态试验分析［9］;巨丽等［10］对击式液压锤进行了模态研究;蔡力钢等［5］对五轴联动重载摆角铣头进行了模态分析与实验研究;宫文峰等［4］采用Polytec激光测振仪对复杂钣金件进行了模态测试。本文以国内某企业试制的某高密度倒装键合头为研究对象，对其进行了模态特性理论计算和模态试验研究。文中以振动理论、模态辨识理论及机械动力学等为理论基础，对键合头进行了三维数字建模、ANSYS有限元模态计算、LMS Test.Lab锤击法模态测试、模态参数辩识和提取，得到键合头准确的模态特性，并给出了键合头的改进措施，研究结果和方法已为某自主研发的倒装芯片键合头结构优化和精度控制提供参考。

1 倒装芯片键合头的三维数字建模

根据倒装键合头的实体结构，运用Solidworks三维设计软件建立了键合头的三维数字模型，如图1所示。键合头具有4个自由度，可以实现上下、左右、前后3个方向的线运动和拾取头绕Z轴作±90°的转动，用来完成芯片的拾取、传送和键合等往复快速动作。前后和左右方向的运动由直线电机驱动，上下方向的运动由伺服电机配合丝杠驱动，拾取头旋转由微调电机驱动，定位精度由光栅尺实时监测并反馈给控制系统，形成闭环精确控制。为确保键合头的工作精度和效率，通常要求其应具有足够的强度、刚度和良好的动态特性。

图1 键合头结构图

2 研究方法

模态分析是研究振动特性的基础，每一阶模态具有特定的固有频率、阻尼和振型［3］。本文建立了键合头模态特性研究系统模型，该模型采用理论计算与实验测试相结合的方法，并综合考虑了键合头在自由悬挂和原装固定两种状态，并将仿真与实测结果做一致性比较，试图得到键合头准确的模态参数、刚度分布情况和影响因素。本模型先以计算结果为参考指导模态实验，再以测试结果验证仿真的有效性，最后将两者结果作一致性比较，当两者结果偏差较大时，以实测结果为参考对仿真模型进行修正，使仿真模型能较好地反映实际键合头的结构特性，修正后的仿真模型再进行后续的结构优化和多物理场耦合等分析所得到的结果将具有较高的可信性，所以不必再进行大量的重复性试验验证，从而缩短了产品的研发周期，降低了研发成本。研究方法框图如图2所示。

3 键合头理论模态研究

3.1 键合头有限元建模

为提高有限元建模的效率和可移植性，本文采用了联合建模的方法。根据键合头的实际结构，文中运用Solidworks建立其三维数字模型，并另存为Parasolid(*.x_t)格式，运用接口技术将其导入ANSYS Workbench中建立有限元模型。键合头属于三维对称组合实体结构，为保证计算效率和收敛性，对规则形体划分为20结点的六面体网格(SOLID186)，对不规则形体划分为10结点的四面体网格(SOLID187)，薄壳体划分为4节点的四边形壳单元(SHELL181)。未经简化的键合头实体模型如图3(a)所示，为提高计算效率，对键合头上小尺寸的倒角、倒圆、工艺孔、螺栓孔等进行简化，简化后的模型如图3(b)所示，有限元网格划分模型如图4所示。有限元网格数据如表1所示，共包含有218178个结点和79098个单元。

图2 键合头模态特性研究系统模型

图3 键合头三维模型

图4 键合头网格划分

表1 键合头有限元网格参数

3.2 理论模态计算求解方程

键合头是一个具有无限多自由度的振动系统，理论上存在无限多阶次的模态固有频率［4］。有限元求解即是将连续系统离散为有限单元和节点，分别计算每个单元的质量矩阵［M］和刚度矩阵［K］，最后集合叠加成统一总质量和总刚度矩阵，其系统运动微分方程可表示为

{X}——节点位移向量;

{F(t)}——载荷向量。

有限元模态计算中通常不考虑外载荷，且阻尼因素对固有频率的影响较小，因此，将式(1)简化为无阻尼自由振动微分方程:

设式(2)解的形式为

式中:{A}——振幅列阵;

ω——振幅{A}的振动频率;

φ——初相位。

将式(3)代入式(2)得

频率特征方程即为

求解式(5)的行列式即可得到n个特征值，对特征值开平方即可得到系统的固有频率ω，第i阶模态圆频率为，将ωi代入式(4)求得非零解{A(i)}，即为第i阶模态振型。

3.3 理论模态计算结果与分析

根据键合头的实际安装工况，文中进行了约束模态理论计算，将键合头底座下底板固定约束，仿真的边界条件设置与实验测试相对应，以便于根据仿真结果指导模态试验。为提高计算效率和解的收敛性，在ANSYS中选用Frequency Finder模态求解器进行求解，计算得到键合头前6阶主振型如图5所示，前6阶固有频率和相应的振型描述如表2所示。

表2 键合头前6阶固有频率和振型描述

从振型图和振型动画上可以看出，键合头前3阶振型中变形最为活跃的位置发生在拾取臂末端处，尤其是第3阶模态呈现为拾取臂的局部弯曲变形，此结果与键合头实际工作时采用高速相机测取的结果相吻合，这与拾取臂的长悬臂结构有很大关系，建议对此处改为短悬壁结构或增加肋板尺寸和数量来提高拾取臂结构刚度;2阶模态振型图中还显示了键合头底座光栅尺连接板的局部摆动变形，此变形将直接影响键合头的监测控制精度，此处应添加肋板提高刚度;后3阶振型为组合变形，也显示出拾取臂为最薄弱环节。计算得到键合头1阶固有频率为347.26 Hz，而与键合头所接近的驱动伺服电机转速为0～10 000 r/min，远高于此工作范围所对应的激振频率，因此键合头不会与周围激振源发生共振现象。

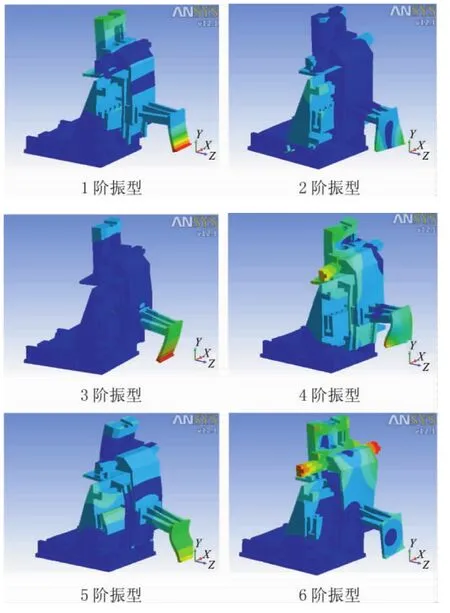
图5 键合头前6阶振型图

4 键合头试验模态研究

4.1 实验模态测试方法

为获取键合头准确的模态特性，在理论模态计算结果的指导下再进行试验模态研究，并以测试结果验证理论计算的正确性，从而得到键合头完整的模态参数、薄弱环节和影响因素。本模态试验采用了业内最先进的模态测试系统，主要包括:比利时LMS数据采集仪、德国Polytec单点式激光测振仪、LMS Test.Lab锤击测试软件、LMS冲击力锤、PCB－356A16型压电式三向加速度传感器、力传感器等测试器材。

本模态实验为提高测试效率和准确性采用了联合测试的方法，以冲击力锤作为激振工具，在数据采集上结合使用了接触式加速度传感器和非接触的激光测振仪，并对两种数采手段进行一致性对比，得到两者获取的数据基本一致的结论。根据键合头的结构特点和实验条件，采用单点激振多点拾振(SIMO)的方法，使用力锤敲击键合头拾取臂末端左测点(图7的B5∶13号点)，将4个三向加速度传感器作为一组移步测试键合头主要部件、将3个单向加速度传感器作为一组测试键合头次要部件、激光测振仪用于采集不易贴装传感器的测点，并在测试软件中设置各传感器的灵敏度。本模态实验的测试系统图如图6所示。

图6 实验模态测试系统框图

图7 键合头测点框线图

在LMS Test.Lab－Impact Testing界面中根据键合头的实际尺寸定义每个测点的位置，并建立键合头测试框线图如图7所示。测点的布置原则为:采用尽可能少的测点获得尽可能形象的振型特征，重要位置多布点，一般位置少布点。

为避免测试信号发生频率混叠，根据香农采样定理，信号的采样频率不得低于欲分析最高频率的2倍。实验时的采样频率根据仿真计算前6阶最高固频的2倍取整设置，仿真中最高分段频率为0～2 000Hz，本试验采样频率为4 096Hz。对响应信号添加指数窗函数，对力信号添加力－指数窗函数。测试过程中采用4次平均处理，由测试系统自动检查并拒绝过载和连击现象，锤击过程可实时监测相干曲线，考察测试的可靠性，如图8所示。

图8 锤击测试相干曲线图

4.2 实验模态测试结果与分析

通过对键合头在安装工况下进行模态测试，最终提取了键合头的前6阶模态。图9为测试得到的模态识别状态图，表3给出了图9中的字母代表的5种状态，在状态图中根据经验识别出较优的频率波峰。表4为本试验模态提取的键合头前6阶固有频率、阻尼比和振型描述，相对应的前6阶模态振型如图10所示。本测试所得到的各阶固有频率所对应的阻尼比均在4%以下，说明所提取的各阶次模态准确性较好。

图9 键合头模态识别状态图

表3 模态状态识别图符号含义

表4 键合头试验模态识别参数和振型描述

图10 键合头试验模态前6阶振型图

从以上实测所得的振型图和动画可以看出，实验所得到的振型图基本上能反映每阶模态的变动趋势，其中前4阶振型的变动规律性较好;键合头整机也存在一定的变形，主要变化表现为拾取臂的摆动、弯曲、扭转等组合变形。总体上看本试验所定义的测点和建立的框线图可以较好地反映键合头的振动型态，基本符合实验要求。

5 理论模态与试验模态结果对比分析

本研究采用有限元仿真和实验测试相结合的方法获取了键合头在安装工况状态下的模态特性。通常有限元计算中，所有的模型元件都参与计算且装配体结合面特性难以有效仿真，因此仿真得到的固有频率往往与真值有一定的偏差量，结构阻尼参数很难获取，但得到的模态振型较为准确;试验模态中可以根据要求在所关心的结构件上布置传感器获取精度相对较高的固有频率值，且可获取结构的阻尼参数，但是振型动画常因测点数量和位置限制而易失真，因此采用仿真与试验相结合的方法可以更好地获取键合头准确的模态特性。本研究分别得到了仿真与试验下键合头的前6阶模态参数。表5统计对比了仿真与测试获得的键合头前6阶固有频率数据。

表5 键合头仿真与试验的固有频率对比

从表5可以看出，试验测得的前6阶固有频率与仿真计算得到的前6阶固有频率比较接近。试验所得频率与理论计算频率误差在9.5%以内，尤其最为关心的1阶固有频率误差仅为6.53%。误差主要由于仿真模型简化了部分小特征，且结合面的设置存在一定的假设，但是误差值在允许的范围内，因此可以认为本研究的前6阶固有频率是可信的［4］。从仿真与试验所得到的振型图看，由图5和图10对比可知，实验测试得到的前6阶振型与仿真计算得到的振型相似度很高，尤其前4阶实测振型与仿真振型变动趋势基本吻合，后两阶振型变动规律不是很明显，但变动趋势基本相同。以上结果说明本研究的仿真模型能较好地反映键合头实际的动态特性，可作为后续的结构优化和改进的理论支撑。

6 结束语

本研究采用理论计算与实验测试相结合的方法研究了国内某研究所研发的某倒装芯片键合机的键合头的模态特性，联合使用了ANSYS软件、LMS Test.Lab模态测试系统和Polytec激光测振仪等研究工具，先对键合头进行有限元建模和计算，再以仿真数据指导实验测试，通过将仿真与试验的结果对比分析，得到了该键合头在安装工况下准确的模态参数和影响因素，得到的主要结论如下:

1)从固有频率方面看，键合头的1阶固有频率高于340Hz，而与键合头相接近的驱动伺服电机转速为0～10 000 r/min，远高于此工作范围所对应的激振频率，因此键合头不会与周围激振源发生共振现象。

2)从仿真计算与实验测试的结果对比方面看，两者吻合性较好，理论计算和实验测试的固有频率误差在9.5%以内，尤其1阶固有频率误差仅为6.53%;仿真计算和试验所得前6阶振型图的相似度很高，尤其前4阶实测振型与仿真振型变动趋势基本吻合，因此可以认为本研究的结果是可信的，仿真模型可作为后续结构优化和改进的依据开展工程研究。

3)从振型云图和刚度分布方面看，首先键合头拾取臂的长悬臂结构刚度最为薄弱，振动趋势较明显，建议将此处改为短悬壁结构或增加肋板尺寸和数量来提高拾取臂结构刚度;其次，键合头底座光栅尺的“工字型”连接板的刚度也不足，将直接影响键合头的控制精度，建议此处添加肋板提高刚度。本研究可为键合头进一步结构优化、多物理场耦合和精度控制以及整机的防振、抑振等提供了理论支撑和实验依据。

［1］REZA A.Semiconductor backend flip chip processing，inspection requirements and challenges［J］.SEMI IEEE: IEMT，2002，(4):18－22.

［2］RILEY G A.Flip chip advantage for complex electronics in micro－systems［C］//Proceedings of the SPIE Conference on Micro－robotics and Micro－assembly，1999.

［3］GONG W F，HUANG M F，CHEN L L，et al.Dynamic characteristics analysis of the flip chip bonding head based on multiple working conditions［C］//International Conference on Electronic Packaging Technology.IEEE，2013:732－737.

［4］宫文峰，黄美发.倒装键合机支撑板模态参数提取与实验验证［J］.中国测试，2014，40(5):145－148，152.

［5］蔡力钢，马仕明，赵永胜，等.重载摆角铣头模态分析与实验研究［J］.振动与冲击，2011，30(7):250－255.

［6］MASSA F，TISON T，LALLEMAND B.Fuzzy modal analysis:prediction of experimental behaviors［J］.Journal of Sound and Vibration，2009，322:135－154.

［7］KROMULSKI J，HOJAN E.An application of two experimental modal analysis methods for the determination of operational deflection shapes［J］.Journal of Sound and Vibration，1996，196(4):429－438.

［8］PINTELON R，GUILLAUME P，SCHOUKEN J.Uncertainty calculation in(operational)modal analysis［J］.Mechanical Systems and Signal Processing，2007(21): 2359－2373.

［9］YING H Q，LIU J M，AO Q B，et al.Small rockets exciting Qian Tang great bridge for modal analysis［C］//17th IMAC，1999:2015－2060.

［10］巨丽，李永堂.对击式液压锤理论与试验模态分析［J］.机械工程学报，2009，45(1):273－281.

(编辑:李妮)

Modal characteristic research and experimental analysis of flip chip bonding head

GONG Wenfeng1，HUANG Meifa2，ZHANG Meiling1
(1.School of Marine Information Engineering，Guilin University of Electronic and Technology，Beihai 536000，China;2.ADMT Key Laboratory of Guangxi，Guilin University of Electronic and Technology，Guilin 541004，China)

Bonding head in FCB is one of the most important functional components used to deal with the process of chip picking，dispensing，and bonding.Since both resonance and additional vibration in bonding head directly affect the working precision，therefore，it is very meaningful to investigate its vibration characteristics.In order to develop high performance chip bonder，the modality characteristics of bonding head under the assembly condition are investigated by simulation calculation and experiment test.In this paper，the modal characteristic system model is established，and the theory of calculate modality and experimental modality are introduced.Experimental and theoretical analysis results were compared and discussed.Exact modal characteristics，weak link and its influential factors of bonding head are obtained.This research result provides a theoretical support and experiment reference for optimizing structure，preventing resonance and reduces vibration of bonding head.

flip chip bonder;modal analysis;harmmering test;finite element method

A

1674－5124(2016)11－0119－07

10.11857/j.issn.1674－5124.2016.11.024

2015－12－27;

2016－02－18

国家自然科学基金(51365009，50865003);十一五国家重大专项02专项(2012ZX02601)

宫文峰(1987－)，男，山东泰安市人，工程师，硕士，研究方向为机械振动与CAE技术、微电子封装与组装技术、先进制造与精密测量技术。

黄美发(1962－)，男，广西蒙山县人，教授，博士生导师，研究方向为机电系统精度设计和智能测量方法等。