轨道梁特性对磁浮车轨相互作用研究

杜振军，李奕璠，林建辉

(1.神华准能集团公司，内蒙古鄂尔多斯010300;2.西南交通大学机械工程学院，四川峨眉山614202; 3.西南交通大学牵引动力国家重点实验室，四川成都610031)

轨道梁特性对磁浮车轨相互作用研究

杜振军1，李奕璠2，林建辉3

(1.神华准能集团公司，内蒙古鄂尔多斯010300;2.西南交通大学机械工程学院，四川峨眉山614202; 3.西南交通大学牵引动力国家重点实验室，四川成都610031)

为缓解磁浮系统车轨耦合振动，目前往往采用增大轨道梁质量的方法来降低车轨系统耦合所带来的不利影响，但在研究过程中却忽略轨道梁刚度及车辆运行速度的变化对车桥振动的影响。为此，该文首先介绍磁浮轨道梁结构、特性要求以及车轨相互作用方式;然后采用车辆轨道垂向耦合动力学模型，仿真分析轨道梁刚度和车辆运行速度对磁浮车辆与轨道之间相互作用的影响。研究表明:轨道梁刚度对车轨振动响应影响较大，同时车速的影响也不能忽略。为以后轨道梁设计、安装及分析磁浮车轨相互作用提供一定的参考价值。

磁浮车辆;轨道梁;车轨相互作用;振动响应

0 引言

磁浮列车是一种无接触运行的新型轨道交通工具，车辆通过电磁悬浮系统与轨道梁相互作用实现车辆的悬浮。轨道梁是磁浮系统的主要承重和传力结构，是磁浮系统最关键的技术之一，是分析车轨相互作用不可避免的重点内容。

为缓解磁浮车轨耦合振动，在实际工程应用中往往增大轨道梁质量及安装刚度来缓解车轨系统耦合所带来的问题，但这必将导致建设成本的大幅提高，国内外已发生多起因轨道梁弹性不足而引发车/轨耦合振动事故［1－2］。早期学者对轨道梁特性影响车轨耦合作用进行了研究。文献［3］介绍了磁浮交通轨道梁的一般结构特性，探讨了影响轨道梁设计的轨道不平顺及轨道梁刚度特性，为轨道梁的设计提供参考。文献［4］分析了磁浮列车过桥时车桥动力作用规律，研究了轨道梁刚度对列车走行性的影响，对轨道梁刚度设计提出建议。文献［5］以德国Transrapid磁浮列车系统为基础，建立轨道梁有限元模型、磁浮车轨垂向耦合系统模型，分析了轨道梁型式、支承刚度等对磁浮车/轨耦合系统动力响应的影响，并得到相关结论。但对于磁浮列车车轨作用方式、轨道梁刚度及车辆运行速度对车桥振动的影响鲜见报道。

本文首先介绍磁浮轨道梁结构、特性要求以及车轨相互作用方式，采用耦合动力学思想，结合车轨垂向耦合模型，仿真分析轨道梁刚度及车辆运行速度对磁浮车辆与轨道之间相互作用的影响。

1 轨道梁概述

1.1 轨道梁结构及车轨作用方式

磁浮轨道结构分为低置轨道结构和高架轨道结构，两种轨道结构均由轨道梁、轨道功能件及下部支承结构组成［6］。高架轨道结构下部支承有桥墩结构，轨道梁通过轨枕架设在高架桥梁结构上。为满足轨道梁刚度要求及降低工程造价，轨道梁一般采用混凝土简支梁或多跨连续梁。

磁浮车辆通过悬浮电磁铁与轨道F轨相互吸引将车辆向上吸起，并通过控制系统的线圈电流保证稳定的悬浮间隙，电磁铁与轨道的悬浮间隙一般控制在10mm［7］。车辆通过悬浮控制系统实现车辆－悬浮系统－轨道梁的相互作用。

1.2 轨道梁特性要求

轨道梁刚度动力特性要求:1)简支轨道梁的竖向挠跨比＜L/4 800;且横向挠跨比＜L/18 000。另一方面要求轨道梁一阶自振频率f必须大于1.1倍的列车运行速度与轨道梁跨度之比［1］，以减小轨道结构在磁浮列车运行时的动力反应，即:

式中:v——车辆运行速度，m/s;

L——轨道梁1阶固有频率单波距离，m。

为减小轨道梁的长波误差及因安装等造成的周期性激扰对车轨相互作用产生的影响，对轨道梁的安装及加工还提出了其他具体要求［8］。例如，简支轨道梁长波误差≤1 mm，相邻轨道梁梁端定子铁心的坡度变化≤0.75 mm/m，相邻轨道梁梁端定子铁心的垂向错位≤0.6 mm。

2 车轨相互作用模型

研究轨道梁特性对磁浮车轨相互作用影响，采用耦合动力学思想，将车辆、悬浮控制、轨道梁系统作为一个整体系统加以研究。根据文献［2］建立磁浮车/轨垂向耦合模型。轨道梁模型采用跨长24m的Euler－Bernoulli简支梁，如图1所示。

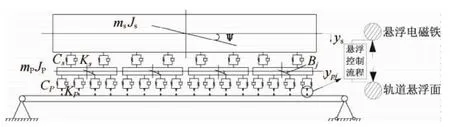
图1 磁浮车辆－悬浮控制－桥梁相互作用模型

2.1 车辆模型

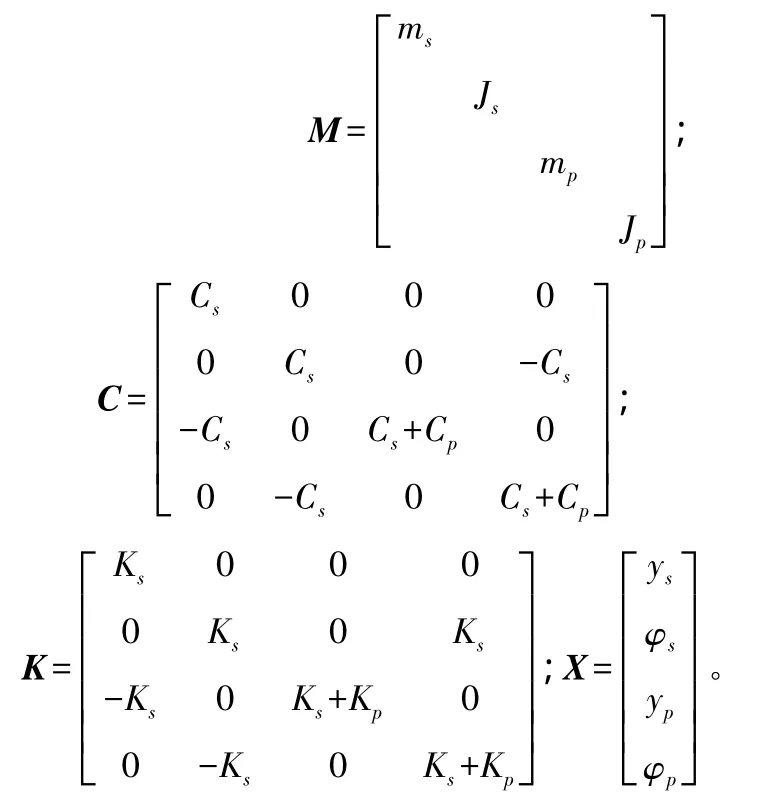
对于车辆模型，考虑车体和悬浮架的点头、沉浮两个自由度，建立车辆动力学方程:

式中:M、C、K——车辆质量、悬挂阻尼、悬挂刚度矩阵;

分别为车体、悬浮架的点头、垂向沉浮位移;

F——作用于车辆系统的电磁悬浮力。

其中:

2.2 轨道梁模型

轨道梁弹性振动及挠度弯曲，均会对车/轨相互作用产生影响。将轨道梁的重力平衡位置视为其初始位置，采用Bernoulli－Euler简支梁模型［7］，其动力学方程为:

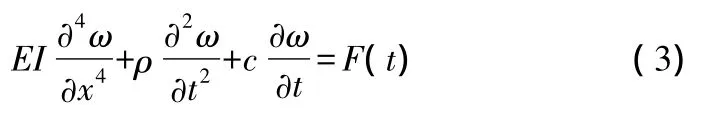
式中:EI——桥梁抗弯刚度;

c——结构阻尼;

ρ——每延米质量;

F(t)——作用在桥上的外力，对于磁浮车桥系统而言，

F(t)为悬浮系统的电磁悬浮力。

3 轨道梁载荷方式

磁浮列车车轨相互作用的竖向荷载基本为均布载荷，车辆编组运行时可以视为多个集中的、可以移动的均布荷载来模拟磁浮列车的动荷载作用。列车在运行过程中，轨道梁的接头、错位等都会对轨道梁产生很大冲击。英国Birmingham机场磁浮系统设计，规定轨道梁承受最大冲击力工况为磁浮车辆从悬浮3 mm处突然落到轨道梁上［9］。

在实际过程中，轨道梁变形［10］主要由两部分组成:1)轨道梁的静挠度，轨道梁建造过程中产生的安装误差、沉降等; 2)车辆荷载在运行过程中轨道梁产生的挠度。因此，轨道梁变形可表示为

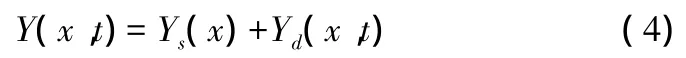
式中:Y(x，t)——轨道梁的总弯曲挠度;

Ys(x)——轨道梁的静挠度;

Yd(x，t)——车辆行驶在轨道上时的动挠度。

磁浮车辆以一定速度通过桥梁时，可以认为车体质量以一定速度依次通过桥梁跨中处。车速不同，跨中处受到外力时间间隔(频率)不同。此外，根据弹性梁的挠度特性［4］，车辆通过桥梁时，质量点作用于跨中处外力的大小总是从小到大，其变化规律类似于一个简谐函数。设车辆以速度v行驶在跨长为L的轨道梁上，则轨道梁的挠度可表示为

4 仿真计算分析

4.1 轨道刚度对车桥振动影响

首先选用两种不同参数的轨道梁，如表1所示，通过改变抗弯刚度以改变轨道梁弹性。

表1 两种轨道梁参数

仿真计算车辆以50km/h的速度通过桥梁，不同刚度对轨道梁及车辆悬浮电磁铁的影响，如图2～图5所示。

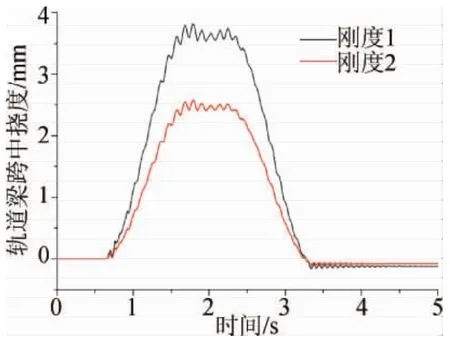
图2 轨道梁的跨中挠度

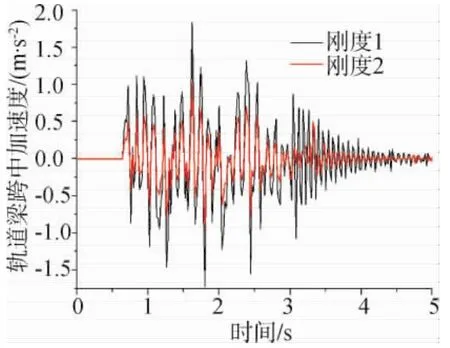
图3 轨道梁跨中振动加速度

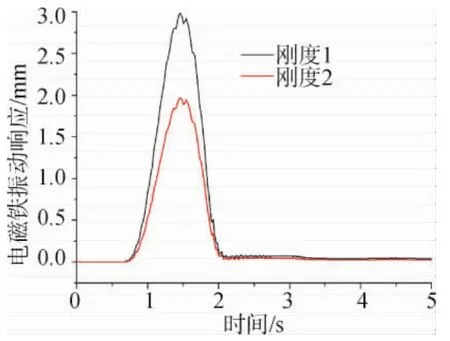
图4 电磁铁振动响应

通过分析发现，轨道梁刚度对车轨相互作用有重要影响，车辆运行在刚度1的轨道梁上时，轨道梁跨中挠度大约在3.75mm，最大跨中振动加速度约为1.5km/s2，此时电磁铁振动响应和加最大速度分别约为3mm和1.5km/s2，当车辆运行在刚度2的轨道梁上时，轨道梁跨中挠度和最大跨中振动加速度分别约为2.3mm和1km/s2，而电磁铁振动响应和最大加速度分别约为2mm和0.75km/s2。可见，与车辆相互作用时，轨道梁刚度越大，则跨中振动挠度和悬浮电磁铁振动响应越大，但是轨道梁刚度对轨道梁的振动加速度影响却不明显。电磁铁受其悬挂刚度的影响，振动加速度也略有减小。

4.2 车辆运行速度对车桥振动影响

车桥相互作用时间即为车辆在桥梁上运行时间，因此车速对车桥作用有一定的影响，车速越大，车桥作用时间越小，车桥相互作用频率越大［7］，因此，车速变化对车桥相互作用响应将有所变化。现仿真分析车速以50，100，150，200，250，300 km/h运行时，车桥振动响应的变化规律，如图6、图7所示。

图5 电磁铁振动加速度

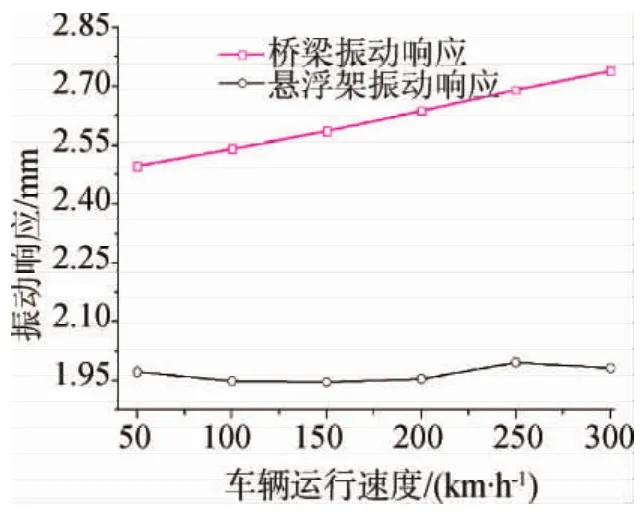
图6 速度对振动响应的影响

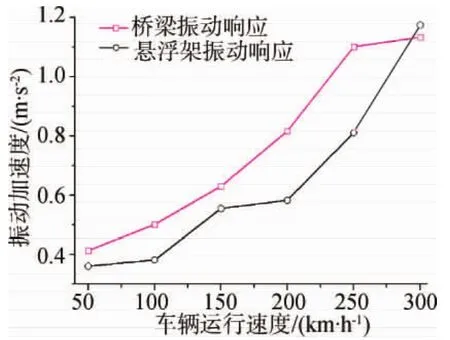
图7 速度对振动加速度的影响

通过分析发现，车速对轨道梁、电磁铁的振动响应影响较小，车速50km/h时，轨道梁振动响应约为2.48mm，车速增至300km/h时，轨道梁响应增至2.78mm，变化增值仅为0.3mm。而电磁铁振动基本保持不变，其响应基本维持在2mm。这主要是由于电磁铁悬挂刚度的影响。就振动加速度而言，车速对两者的振动加速度影响较大，车速50km/h时，轨道梁和电磁铁的振动加速度约为0.41km/s2和0.38km/s2，当车速增至300km/h时，加速度变为1.18km/s2和1.2km/ s2，由此可见车辆运行速度对振动加速度却有较大的影响。

5 结束语

通过对磁浮轨道梁结构、轨道梁特性要求及车轨作用方式的阐述，分析了磁浮轨道的载荷方式，采用耦合动力学思想，结合车轨垂向耦合模型，仿真分析了轨道梁刚度及车辆运行速度对车轨相互作用的影响规律发现:

1)磁浮车辆是以均布荷载的方式作用于轨道梁。当车辆通过桥梁时，可视为一系列均布荷载以一定速度通过桥梁，其对轨道梁跨中的影响规律类似于一个简谐函数。

2)轨道梁刚度对车轨振动响应有较大影响，尤其对车辆、轨道梁的振动振幅作用更为明显，对其两者振动加速度影响较小。

3)车辆运行速度对车辆、轨道梁振动也有所影响，但是车速对两者振动振幅影响较小，特别是对电磁铁振动基本没有影响，而对两者振动加速度均有较大影响。

［1］梁鑫.磁浮列车车轨耦合振动分析及试验研究［D］.成都:西南交通大学，2015.

［2］ZHOU D Z，LI J，ZHANG K.Amplitude control of the trackinduced self－excited vibration for a maglev system［J］.ISA Transactions，2014，53(5):1463－1469.

［3］余华，吴定俊.磁浮交通线的轨道梁结构及动力特性［J］.城市轨道交通研究，2006，(9):38－40.

［4］余华.磁悬浮轨道梁刚度对列车走行性影响研究［J］.铁道标准设计，2005，(1):65－68.

［5］吴范玉，高亮，魏庆朝.高架轨道梁结构特性对磁浮系统的动力影响［J］.工程力学，2004，(4):144－149.

［6］HAN J，KIM J，SONG S.Fatigue strengthevaluation of a bogie frame for urban maglev train with fatigue test on full－scale test rig［J］.Engineering Failure Analysis，2013，(31):412－420.

［7］邓亚士，魏庆朝，时瑾.高速磁浮桥上轨道梁振动特性初步研究［J］.振动工程学报，2008，21(3):248－254.

［8］熊文，祝兵.磁悬浮轨道梁的动力响应分析［J］.四川建筑，2005，(4):65－67.

［9］沈锐利.高速铁路简支梁竖向振动响应研究［J］.中国铁道科学，1996，(3):24－34.

［10］CAI Y，CHEN S S.Vehicle/Guideway Dynamic Interaction in Maglev Systems［J］.Transactions of the ASME，1996，(118): 526－530.

(编辑:李妮)

Analysis of track beam characteristics on the maglev vehicle－track interaction

DU Zhenjun1，LI Yifan2，LIN Jianhui3
(1.Shenhua Group Zhungeer Energy Co.，Ltd.，Ordos 010300，China; 2.School of Mechanical Engineering，Southwest Jiaotong University，E'meishan 614202，China; 3.State Key Laboratory of Traction Power，Southwest Jiaotong University，Chengdu 610031，China)

In order to relieve the coupled vibration between vehicle and track system，increasing of the quality of guideway is often used nowadays to decrease the adverse influence caused by vehicle－track coupled vibration.However，the effect of guideway stiffness and operation speed on vehicle and track vibration is neglected in the researches.In this paper，the maglev guideway’s structure，characteristics required and the mode of interaction were introduced firstly.And then，vehicle－track coupled dynamics model was developed to analysis the influence of track beam stiffness and vehicle speed on maglev vehicle－track interaction.The study results showed that the stiffness of track beam impacted the vehicle－track vibration greatly，at the same time the influence of speed also could not be ignored.These conclusions can provide a certain reference value for guideway design，installation as well as analyzing the maglev vehicle－track interaction.

maglev vehicles;guideway;vehicle－track interaction;vibration response

A

1674－5124(2016)11－0131－04

10.11857/j.issn.1674－5124.2016.11.026

2015－12－10;

2016－02－03

中央高校基本科研业务专项资金资助项目(SWJTU2682014BR001EM)国家自然科学基金重点项目(61134002)

杜振军(1972－)，男，内蒙古赤峰市人，高级工程师，硕士，主要从事车辆动力学研究。