机器视觉空间目标姿态自动测量方法研究

游江，唐力伟，邓士杰

(军械工程学院火炮工程系，河北石家庄050003)

机器视觉空间目标姿态自动测量方法研究

游江，唐力伟，邓士杰

(军械工程学院火炮工程系，河北石家庄050003)

针对空间目标姿态测量问题，提出基于机器视觉的空间目标姿态自动测量方法，并对其中较为关键的目标靶自动分割及特征点自动排序问题进行研究。首先改进圆形目标靶的设计，通过设置区域面积及矩形度阈值，实现目标靶的自动分割，并提出基于向量夹角的圆心点阵顺序排序法，实现特征点准确快速地自动排序，最终基于张正友标定法，完成相机标定，获取目标靶在相机坐标系下的旋转矩阵，进而计算目标靶的空间姿态变化。实验结果验证:姿态解算的最大相对误差≤3%，整个姿态解算过程自动化程度较高，平均耗时2.026 s，能够满足工程测试需要。关键词:机器视觉;自动分割;自动排序;向量夹角;姿态测试;

0 引言

随着科技的发展进步，常需要测量空间目标的姿态变化。目前在工程测试领域，按照测试性质主要分为机械测量法［1］、电测量法［2］和光学测量法［3］。其中机械测量法和电测量法较为简单方便，但均为接触式测量，测量效率低，精度较差［4］，特别是在冲击较大的场合，测量结果存在较大误差，并且传统的姿态测量设备和技术在精度、效率及自动化程度上存在局限性［5］。

随着机器视觉技术的发展，由于其具有高精度、非接触、响应快、稳定性好、操作方便灵活等优点，被广泛应用于航空航天、汽车制造，精密测量等领域［6］。机器视觉是通过获取目标不同姿态下的图像信息，基于成像原理，利用特征点坐标关系，恢复目标的三维信息，进而完成测量［7－8］。

为了实现自动化测量，本文提出了一种基于机器视觉的空间目标姿态自动测量方法。首先改进传统目标靶的设计，通过CCD拍摄目标靶的图像信息，设置区域面积和矩形度阈值自动分割目标靶，再利用canny算子检测特征圆边缘，并采用最小二乘法拟合圆心，提出基于向量夹角的特征点顺序排序法，完成圆心点阵的自动排序，最终基于张正友标定法，标定相机，获取目标靶相对相机坐标系的变换矩阵，进而计算目标靶的空间姿态变化。通过CZJC_ 01转角仪，进行实验验证，最大相对误差≤3%，整个姿态解算过程平均耗时2.026 s，具有较高的测量精度和效率，能够满足工程测试要求。

1 目标靶改进设计

目前常用的目标靶多为黑白棋盘格［9］，这种目标靶对图像质量要求较高，并且在畸变较大的场合，角点提取精度较差，不适合工程应用。相反，由于圆形靶标，形状独特，易于提取，因此本文采用实心圆阵目标靶［10－11］。然而传统的圆形目标靶，不便于在复杂背景下的自动提取，且需要人工确定边界点。因此为了实现整个目标靶空间姿态测试的自动化，基于以下准则改进了圆形目标靶。

1)合适的尺寸:保证相机成像时，目标靶尽可能覆盖整个成像区域［12］，从而提高特征点提取精度;

2)目标靶便于和背景分离:目标靶与背景存在颜色、形状等较大差别，便于快速准确的自动分割目标靶;

3)特征点易于提取和排序:保证快速准确获取特征点坐标，且实现目标靶特征点与其投影点的对应;

4)特征点采用合适的算法，便于实现稳定且高精度提取。

相比传统圆形目标靶做了两点改进:

1)增加了10 mm的矩形边框，便于通过检测连通区域的面积及矩形度，设定阈值，实现目标靶自动分割提取;

2)3个边界圆半径按照左上角，左下角，右上角依次为4，12，15 mm，其余圆半径为8 mm，以此可以通过检测特征圆面积，确定边界点;而且可以将边界点作为方位基准，实现圆心点阵的自动排序，最终实现目标靶空间姿态的自动测量。

最终设计的圆形目标靶如图1所示。

图1 目标靶结构

2 目标靶分割及特征圆圆心提取

2.1 目标靶自动分割

为了实现自动化的测量目标空间姿态，首要的就是快速准确的从背景中自动分割提取出目标靶。本文采用基于边缘的图像分割技术，设定区域面积和矩形度阈值，从而实现目标靶的自动分割。

1)区域面积。对标定图像边缘提取后填充，通过设定合适阈值，去除部分非目标靶的封闭区域。

2)矩形度。由于背景中可能存在与目标靶面积相当的连通区域，因此需要进一步通过计算封闭区域的矩形度，将其剔除。通过检测目标靶封闭区域信息，获取包围连通区域所需最小矩形信息以及连通区域总像素数，计算其矩形度r。

其中，narea为连通区域所占像素总数，a、b分别为包围连通区域所需最小矩形的长和宽。通过设定合适的阈值，即可从复杂背景中分割出目标靶。

目标靶分割前后如图2所示。

图2 目标靶自动分割前后对比

2.2 特征圆圆心提取

为了完成相机标定以及空间姿态的测量，必须快速准确的提取特征圆圆心坐标。由3.1节得到的目标靶，通过检测连通区域，可以获取目标靶的特征圆，进而获取圆心坐标。

目前圆心获取常用的两种方法:

1)区域检测，获取特征圆区域，求取区域质心，进而找到椭圆中心。计算简单，实时性较强，但容易受到外界因素干扰，精度和稳定性不高;

2)检测边缘，拟合获取圆心。实时性不高，但对于外界因素的影响具有较高的鲁棒性和提取精度，并可以达到亚像素精度。

为了保证标定精度，本文采用第2种方法，采用canny算子，检测特征圆边缘，最后采用最小二乘法拟合边缘，获取特征圆圆心。

3 基于向量夹角的特征点顺序排序

特征点的正确匹配是实现摄像机自动标定及空间姿态自动测量的关键［13］，直接决定了相机标定以及姿态测量的准确性，因此必须快速且准确的完成目标靶上特征点的自动排序。

3.1 边界点确定

在第2节可以获得目标靶内所有特征圆所占像素数，由目标靶的物理结构可知，3个边界圆与其余特征圆具有不同的尺寸，因此不论目标靶处于何种姿态，以及相机畸变，光照不均等因素影响，均可以根据特征圆所占像素数，确定边界点，记为A、B和C。

3.2 特征点排序

由于镜头畸变，光照不均等问题，实际提取的圆心点阵像素坐标，不具有相同的间隔。由相机畸变模型可知，外围的点间距畸变较大。因此传统的基于交比不变原理设置阈值法，不能满足要求，在畸变较大的场合，会存在排序错乱的情况。

因此提出基于向量夹角的顺序排序法。如图3所示，首先根据边界点，利用边界向量夹角阈值准则，查找边界AB及AC上的特征点，并按照距点A的欧式距离排序，实现边界线上特征点排序;进而依次以AC以及AB对应位置点为基准，基于基准向量夹角阈值准则，查找对应位置特征点，并及时将已匹配点从点阵中去除，提高搜索效率，直到完成所有点的排序。具体步骤如下所示:

图3 特征点排序示意图

1)确定边界点A、B和C，并计算向量AB与AC夹角θ;

2)查找边界线AB及AC上特征点，并排序

①取圆心点阵中任意一点(A、B、C除外)，设为点P，分别计算向量AP与AB、AC夹角，记为θ1、θ2;

②判断，若θ1≤α且，则为边界线AB上点，如点P1，记入L1;

若θ2≤α且，则为边界线AC上点，如点P2，记入H;

否则，即为非边界点，如点P3，记入M;

③分别计算L1及H点与A的欧式距离，并将特征点坐标按照其距离从小到大排列;

④将点A坐标，记入H中，并位于首位;

3)依次以边界线AC上特征点为基准，查找该列上特征点，并排序;

①分别取点Hi及Hi+1(i=1);

②取Li作为基准列，取点，记为Bj(即第i列第j+1行点);

④计算向量HiBj与Hi+1Qk夹角，记为β;

⑤直到j=7，即找到第i+1列中所有行位置点，即Li+1;

⑥将未排序点阵中，去除Li+1对应点;令i=i+1，重复步骤①;

4)最终排序:将H中所有点，对应记入矩阵L每一列的首元素;

目标靶特征点排序前后如图4所示。

图4 特征点阵排序前后示意图

4 相机标定及姿态解算

4.1 相机标定

如图5所示，以目标靶AC边为X轴，以AB边为Y轴，以垂直目标靶平面向外为Z轴，建立随体坐标系(即目标靶坐标系)。

图5 建立随体坐标系示意图

将由排序后的特征点阵像素坐标，及特征点在随体坐标系中的物理坐标，作为Zhang算法标定工具箱［14］的输入，优化相机参数，获取目标靶相对相机坐标系的变换矩阵。

4.2 姿态解算

设随体坐标系X轴与转角仪横轴平行时为初始姿态0，记为C0，由C0绕转角仪横轴(即随体坐标系X轴)旋转α1，再绕Z轴旋转β1，到姿态1，记为C1，由欧拉角空间旋转矩阵变换理论(详见文献［15］)，可知两个姿态间的变换关系为

即初始姿态0到姿态1的真实旋转矩阵为

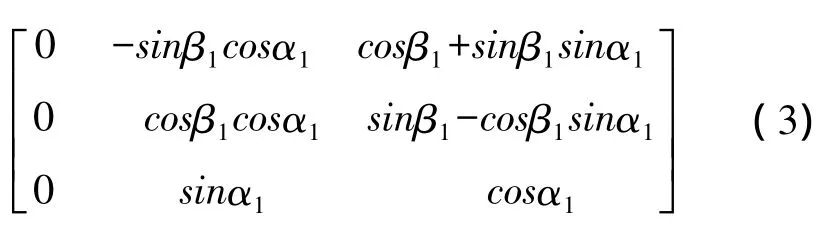
由4.1节相机标定可以获取相机坐标系相对随体坐标系的旋转矩阵和平移向量，设姿态0和姿态1，相对相机坐标系的旋转矩阵分别为Rc0、Rc1。则两个姿态间的变换关系为

即初始姿态0到姿态1的测量获得的旋转矩阵为

则可以求出α1及β1:

5 实验测试

5.1 实验组成

实验系统主要由计算机、面阵CCD，图像采集设备Core，8×8实心圆阵列目标靶，CZJC_01转角测量仪。CCD像元尺寸为5.5μm×5.5μm，像素数为2048×2048;镜头焦距为65～80 mm;相机通过26pins相机接口线与记录采集设备Core进行传输;Core通过e－SATA接口与计算机进行数据交换。测试系统图6所示。

图6 测试系统图

5.2 实验步骤

1)将计算机、采集设备Core及相机，按照正确方式连接，将目标靶固定于CZJC_01转角测量仪;

2)打开计算机，运行CoreView记录软件，对相机初始参数进行设置，使目标靶图像清晰;

3)控制转角测量仪分别沿着X轴、Z轴方向转动，带动靶标转动，同时采集目标靶图像;

4)按照以下流程处理目标靶图像，解算目标靶的空间姿态变化。

流程如图7所示。

图7 目标靶的空间姿态自动解算流程

5.3 实验结果

5.3.1 自动排序算法性能测试

本文改进设计的目标靶，以及提出的排序算法，原理上具有旋转排序适应性。在0°～360°内场景，拍摄不同角度、不同方向和不同光照条件下的目标靶，任意选取25张标定图像进行测试，均未出现排序错乱情况。排序过程的消耗时间如图8所示

图8 自动排序算法用时

由上图可以看出，最大排序时间为0.070 8 s，平均排序时间为0.066 2 s。因此本文的基于向量夹角的顺序排序法，具有较高的运行效率和准确性。

5.3.2 姿态自动测量算法时效性测试

任意选取25张处于不同空间姿态的目标靶图像，按照图7所示的后期姿态自动解算流程处理，计算任两张目标靶间的姿态变化，其涉及的处理步骤、耗时以及需要操作的次数如表1所示(以下各处理环节耗时，除相机标定外，均为平均时间)。

表1 空间姿态变化解算各操作步骤、耗时及次数

由上表可以看出，任意两张目标靶间空间姿态变化解算，平均耗时约为2.026 s，具有较好的时效性，能够满足工程应用。

5.3.3 姿态自动测量算法精度测试

在实验室CZJC_01转角测量仪上，分别绕X、Z轴转动，并分别进行了单方向轴和双方向测试，结果如表2和图9所示(参考值是由转角仪显示结果，测量精度为0.001°)。

表2 转角测试结果

图9 转角测量结果

从测量结果看，随着转角的增大，相对误差越来越小，最大相对误差≤3%。在X(或Z)轴转动时，Z (或X)轴也会有较小的角度变化，主要是由目标靶的安装误差，非绝对平面等因素造成，但附加误差均较小。另外，相比绕X轴转动，绕Z轴转动测量误差较小，特别是在转角较大时，误差相对较大;主要由于绕X轴转动时，目标靶平面与相机成像平面夹角随着X转角增大而变大，致使目标靶在图像占有率较低，特征圆所占像素数较少，圆心提取精度较差，导致相机标定误差较大，进而影响了姿态的解算。

6 结束语

本文基于机器视觉技术，建立了空间目标姿态自动测量系统，改进了目标靶的设计，并通过设置区域面积和矩形度阈值，实现了目标靶的自动分割，并提出基于向量夹角的特征点顺序排序算法，完成圆心点阵的快速准确的自动排序，最终标定相机，计算目标靶姿态变化。实验结果表明:提出的基于向量夹角的特征点顺序排序算法，效率高，稳定性好;最终的姿态解算结果接近真实值，最大误差≤3%，整个姿态解算平均耗时约2.026s，满足工程需要，具有较好的实用价值。

［1］韩冬，何闻.超低频标准振动系统基础设计技术［J］.振动与冲击，2008，27(9):20－22。

［2］滑广军，李强，杨益民，等.某大型超静定框架的动态应力测试与有限元分析［J］.振动与冲击，2008，27(8): 170－172

［3］CHUNG H，LIANG J，KUSHIYAMA S，et al.Digital image processing for non－linear system identification［J］.International Journal of Non－linear Mechanics，2004，39 (5):691－707.

［4］歹英杰，汪伟，邓士杰，等.基于立体机器视觉的动目标空间位姿测试研究［J］.振动与冲击，2015，34(16):188－212.

［5］朱晓林，高诚辉，何炳蔚，等.基于机器视觉的机械零件图像尺寸自动标注方法［J］.中国工程机械学报，2010，8(3):324－328.

［6］张梁，徐锦法，夏青元.双目立体视觉的无人机位姿估计算法及验证［J］.哈尔滨工业大学学报，2014，46(5): 66－72.

［7］陈爱华，高诚辉，何炳蔚.立体视觉中的图像立体匹配算法［J］.中国工程机械学报，2014，12(3):194－198.

［8］郭继平，李阿蒙，于冀平，等.双目立体视觉动态角度测量方法［J］.中国测试，2015，41(7):21－23，36.

［9］SHI X F，HONG N，CAI T F.An automatic and robust chessboard corner extraction［J］.Transaction on Edutainment VI，2011(6758):49－56.

［10］夏仁波，刘伟军，赵吉宾，等.基于圆形标志点的全自动相机标定方法［J］.仪器仪表学报，2009，30(2):368－373.

［11］徐鹏，汪建业，王燕儒.摄像机标定中靶标圆心像点坐标的精确计算［J］.红外与激光工程，2011，40(7):1342－1346.

［12］张春燕，邹伟.一种鱼眼镜头标定板的设计、检测与排序方法［J］.计算机工程与应用，2015，51(15):188－192.

［13］梁力，尹东斐，王川.高精度摄像机标定模板的设计及设别算法［J］.西安交通大学学报，2011，45(4):82－85.

［14］BOUGUET J.Visual methods for three－dimensional modeling［D］.Pasadena:California Institute of Technology，1999.

［15］胡茂林.空间和变换［M］.北京:科学出版社，2007:123－124.

(编辑:刘杨)

Research of automatic measurement method of space target’s posture based on machine vision

YOU Jiang，TANG Liwei，DENG Shijie
(Department of Guns Engineering，Ordnance Engineering College，Shijiazhuang 050003，China)

Aiming at the problem of the measurement of target’s posture，a non－contact automatic measurement system of space posture based on the machine vision was established，and the key steps of automatic division of the target and ranking of the points have been researched.Firstly the design of target was improved，and then the automatic division of the target was realized by setting the area and rectangularity threshold.Then the ranking arithmetic based on vector angle was proposed to realize the fast and exactly automatic ranking of the points.Finally the camera was calibrated by Zhang’s method，and the conversion of the target’s posture was calculated.The experiment result shows that:the largest relative error of the measurement of the posture is no more than 3%，and the automatic testing method is of high automaticity，and the average time of posture testing is about 2.026 s.Therefore the proposed method meets the engineering test requirement.

machine vision;automatic division;automatic ranking;vector angle;posture measurement

A

1674－5124(2016)11－0107－06

10.11857/j.issn.1674－5124.2016.11.022

2016－05－10;

2016－07－15

游江(1992－)，男，河南南阳市人，硕士，主要从事机器视觉及性能测试方面研究。

唐力伟(1961－)，男，天津市人，教授，博导，主要从事兵器性能检测、故障诊断等研究。