无人机两轴云台建模及其自适应容错控制

林　峰，王晓晓，曲晓光

(沈阳航空航天大学 自动化学院，沈阳 110136)



无人机两轴云台建模及其自适应容错控制

林峰，王晓晓，曲晓光

(沈阳航空航天大学 自动化学院，沈阳 110136)

摘要：根据两轴云台框架的运动学和动力学特性推导出它的动力学方程，通过对其进行简化并在平衡点线性化，得到适用于容错控制器设计的数学模型；采用自适应容错控制方法设计两轴框架云台容错控制器，该算法能够实时估计执行器故障，自适应率可进行自动更新用以补偿故障对系统造成的影响。该控制器的闭环扰动容许能力比传统的固定增益控制器的闭环扰动容许能力高，特别是在执行器饱和且有故障的状态下。该算法以线性矩阵不等式的形式得出，利用MATLAB的LMI工具箱计算仿真得出结果。结果表明该容错控制器算法的扰动容许能力强，能够满足无人机载系统稳定安全控制的需要。

关键词：两轴云台；建模；线性矩阵不等式；自适应控制；饱和及故障

无人机云台机载稳定系统在无人机低空遥感技术中发挥着重要的作用，该系统必须消除机载扰动影响和执行器故障等问题才能获得高质量的低空遥感图像，对系统的容错和抗干扰能力有较高的要求。目前国内外对于机载云台的建模和稳定控制得到了较完善的研究，目前已有很多方案。例如，经典控制方法、现代控制方法、智能控制方法[1]。总体来看这些方法都是针对云台的正常工作时的优化稳定，但是机载云台系统对于容错和抗干扰性能的要求却没有得到深入的研究发展。通常为了降低成本，提高组件的使用效率，低空遥感技术大多采用两轴云台系统，而两轴云台系统对稳定和容错技术有较为苛刻的要求。建模问题是云台稳定控制的基础，综合前人三轴云台数学建模的基础上，对两轴云台的动力学和运动学方程平衡点处的线性化得到适用于自适应容错控制的数学模型[2]。为了提高系统的可靠性和安全性，利用从设计角度同时考虑执行器饱和故障问题的自适应H∞容错控制算法，该算法较传统容错算法开放稳定，相对于固定增益控制器设计有更高的抗扰动容许水平和H∞性能。

1两轴云台结构简介

两轴云台有两个转动自由度，在低空遥感中一般选用直角坐标式结构，两轴直角结构从内到外依次是横滚环和俯仰环。滚转框与俯仰框相连，滚转框可以绕俯仰框转动。俯仰框是最外面的框与基座相连，基座固定在无人机上。

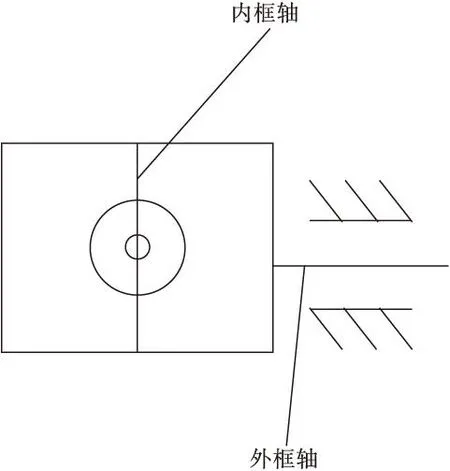
图1　两轴云台框架结构图

2两轴云台数学模型的建立

云台的数学模型是根据云台框架的受力和空间转动工作情况得到运动学和动力学方程。实际框架的运动是空间定点转动和平动的叠加，涵盖了空间的两个转动自由度，若考虑框架的弹性变形就更复杂了，因此为了简化数学模型的推导做如下假设[2]：

(1)忽略弹性形变，假设各框架为刚体。

(2)假设各框架的转轴共点且相邻两轴严格正交。在以上假设的基础上先分析框架的运动关系并建立相应坐标系。

云台安装在无人机的基座上，基座同无人机机体一起相对惯性系平动和转动。定义惯性系坐标为O-XaYaZa；基座固连运动坐标系：O-XbYbZb；俯仰框架固定动坐标系：O-XpYpZp；横滚框架固定动坐标系：O-XrYrZr；其中Xp与Xb重合。p系可以相对于b系转动角度为α；r系可以相对于p系转动角度为θ。

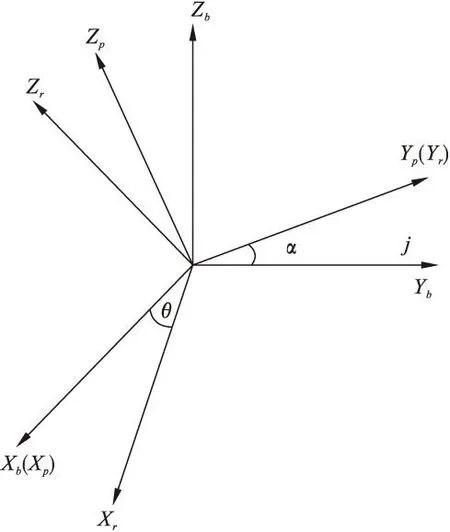
图2　框架坐标图

基坐标系到外框坐标系的变换矩阵:

外框坐标系到内框坐标系的变换

得到在外框坐标系内的外框角速度向量如下：

=[ωpxωpyωpz]T

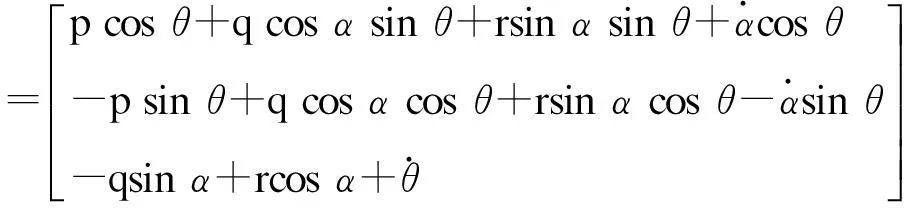
=[ωrxωryωrz]T

Mp=[MpxMpyMpz]T

内外框都为正方形转动惯量为：

Jpx=Jpy=Jpz=0.012 5·N·m/s2/rad

Jrx=Jry=Jrz=0.017 1·N·m/s2/rad

得内框动力学方程：

Mr=[MrxMryMrz]T

2.1框架动力学方程建立

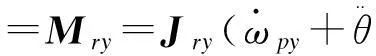
所以得到内外框动力学方程为：

2.2两轴云台框架模型简化及平衡点线性化

由于以上得到的数学模型过于复杂且是非线性的，不便于控制器的设计和仿真，需要进行简化和线性化处理。写成矩阵形式：

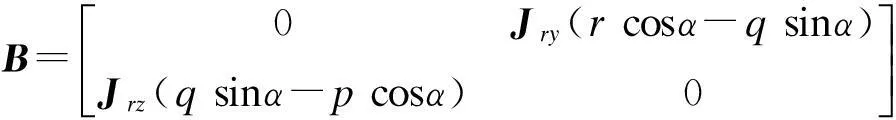
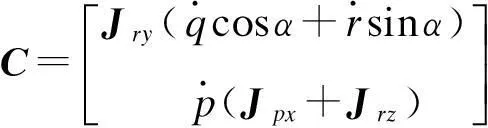
(1)

其中，

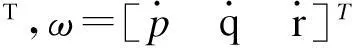
3两轴云台自适应容错控制器设计

3.1执行器饱和与扰动下容错控制的理论知识

无人机云台稳定框架系统是无人机获得高质量的低空遥感影像的关键，云台框架和伺服电机的物理特性会产生一定的调节范围，执行器会存在饱和现象。在无人机姿态改变时会产生一定的干扰和故障，因此云台系统对稳定容错控制技术有较为苛刻的要求。

将两轴云台框架系统的状态方程化成一般的系统状态方程：

Z(t)=Cx(t)+Dσ(u)

(2)

其中，x(t)是云台稳定系统的状态，σ(u)∈Rm是带有饱和现象的云台框架系统的控制输入，ω(t)是系统产生的扰动L2[0,∞]输入。将云台系统(1)的系数矩阵一一对应到(2)的参数矩阵中。

两轴云台系统的饱和非线性化的过程以如下的形式给出[3]：

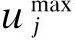
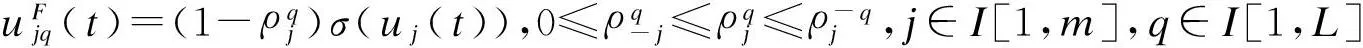
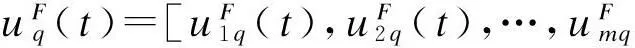
为了本文的表述方便，需要将系统的执行器故障模型进行简化，下式为简化的模型：

uF(t)=(I-ρ)σ(u(t)),ρ∈[ρ1…ρL]，其中，ρ可以表示为ρ=diag[ρ1…ρm]。

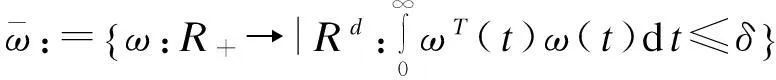
3.2两轴云台控制系统的设计

两轴云台系统可以转化成带有执行器故障和执行器饱和现象的系统：

z(t)=Cx(t)+D(1-ρ)σ(u(t))

控制器可以设成带有自适应参数调节的结构，如下：

(3)

故系统在带有饱和的状态下的线性反馈可以描述成如下等式[3]：

(4)

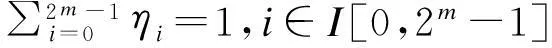
(5)

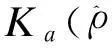
(6)

(7)

对∀x(t)∈ε*(P,δ*)⊂系统模型和系统控制器所组成的闭环系统：

(8)

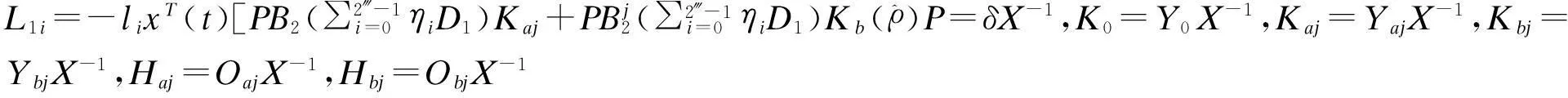
(9)

注：γn表示两轴云台系统无故障下的自适应H∞性能水平。γf为两轴云台系统有故障模式下的自适应H∞性能指标。δ为系统的容许扰动水平。这样，求解γn和γf以及δ即可。

通过如下算最优化过程来得到最小化指标γf和γn，最大化的δ：

minη=αηn+βηf+γηδ

s.t.(a)

(10)

(b)ε*(P,δ*)⊂,

(11)

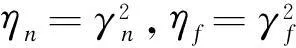
其中α，β,γ是加权系数。

算法：(1)求解最优化问题：minη=αηn+βηf+γηδs.t.(a)(8),b(2)最优解得到ηn，ηf，ηδ，X，Y0，Yaj，Ybj，O0，Oaj以及Obj其中j∈I[1,m]，继续式(2)。

(2)控制器的相关参数K0,Kaj,Kbj，j∈I[1,m],通过式(9)确定。

(3)确定系统的自适应律式(8)。可以发现自适应容错H∞控制器的设计与固定增益H∞控制的设计条件更自由。

表1　两轴云台参数表

3.3控制算法在两轴云台系统中的应用

对于某两轴云台系统取：p=0.087 5rad/s，r=0.052 5rad/s；将参数带入得到两轴云台容错控制状态矩阵为：

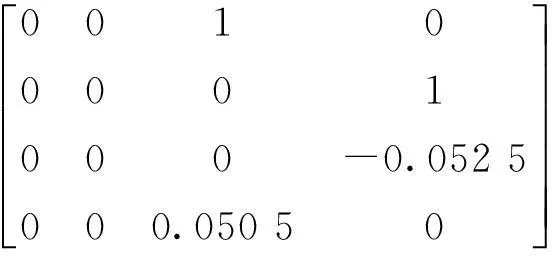
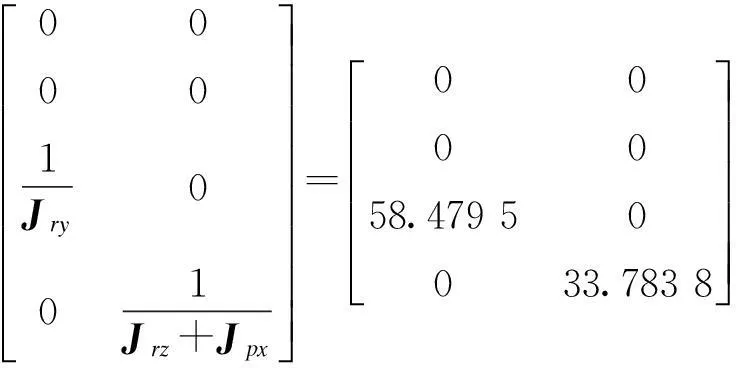
云台稳定系统的执行器存在两种模式：正常模式和故障模式。

设定加权参数为α=0.5，β=0.01，γ=0.5,调用Matlab中的LMI工具箱来求解，固定增益控制器设计方法得到ηn=16.3668,ηf=490.4561,ηδ=26.1502；而在自适应H∞的控制算法中得到ηn=11.3668,ηf=100.6399,ηδ=1.4438；这一现象说明本文给出的自适应H∞控制器设计方法比较固定H∞控制器设计方法有更高的优越性。

为了表明提出方法的有效性，首先给出系统状态反馈情况仿真。在以下仿真中考虑如下故障模式：在0秒，其中一个执行器中断，此处我们选择l1=l2=100。首先我们考虑系统的H∞性能。给出如下形式的扰动：

图3与图 4 分别是系统的第一个状态在自适应H∞控制器及增益H∞控制器下正常模式和故障模式下的状态轨迹；图 5 与图 6 分别是系统的第二个状态在自适应H∞控制器及增益H∞控制器下正常模式和故障模式下的状态轨迹。

显然，自适应H∞控制器的状态曲线比固定增益H∞控制器下云台系统的状态响应曲线有更好的效果，这也验证了本文自适应H∞控制器理论结果的优越性。

考虑扰动容许问题，在以下仿真中选择如下扰动:

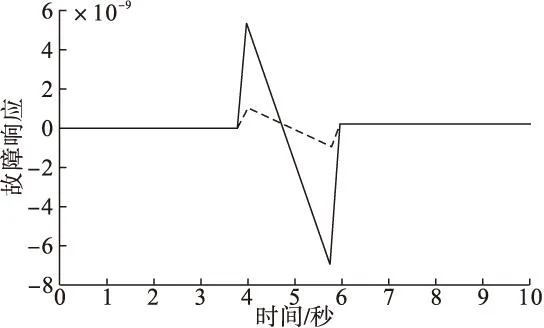
图3　第一个状态在正常模式下的响应曲线(虚线为

图4　第一个状态在故障模式下的响应曲线(虚线为

图5　第二个状态在正常模式下的响应曲线(虚线为

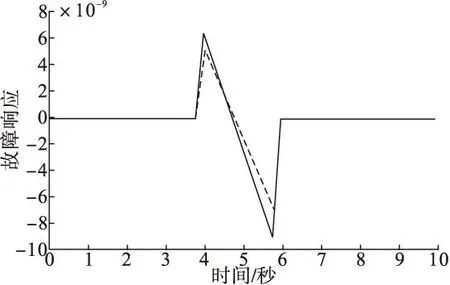
图6　第二个状态在故障模式下的响应曲线(虚线为

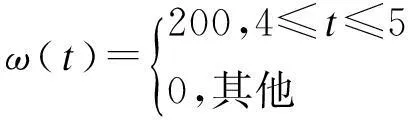
(12)

图 7 给出了闭环系统在自适应H∞控制器正常模式下的状态曲线。图8给出了闭环系统在固定增益H∞控制器正常模式下的状态曲线。显然，在扰动(12)下，在自适应H∞控制器的作用下闭环系统仍然是渐进稳定的，但是在固定增益H∞控制器下的闭环系统却发散了。这一现象说明本文中的自适应设计方法有更好的效果。

图7　正常模式下，系统在自适应控制器作用下的状态

通过以上仿真结果可以看出，本文在状态反馈条件下提出的自适应设计方法较已有的固定增益控制器设计方法有一定的优越性。首先，综合考虑执行器故障和饱和两种情况，然后得到了比固定增益控制器设计方法更好的性能和扰动水平。

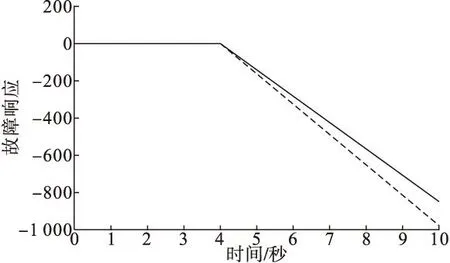
图8正常模式下，系统在固定增益控制器作用下的状态响应曲线(实线为第一个状态，虚线为第二个状态)

4结论

根据两自由度云台框架稳定平台动力学特性，建立了适用于容错控制器设计的线性化模型。在线性矩阵不等式的理论框架下利用自适应容错控制器设计方法，该方法可以保证云台系统在执行器饱和及执行器故障情况下的扰动容许水平及自适应性能。本文的仿真结果表明自适应容错控制器方法相对于固定增益控制器方法更能保证云台系统的稳定。

参考文献(References)：

[1]张平.机载/弹载视觉导引稳定平台的建模与控制[M].北京:国防工业出版社,2011.

[2]刘珊中,孙隆和,车宏,等.机载光电跟瞄平台建模及其H∞稳定控制[J].系统仿真学报，2008,20(6):1518-1521.

[3]关威.基于LMI技术的受限系统稳定性分析与容错控制[D].沈阳：东北大学,2008.

[4]MAYBECK P S.Multiple model adaptive algorithm for detecting and compensating sensor and actuator/surface failures in aircraft flight control systems[J].International Journal of Robust and Nonlinear Control,1999,9(14):1051-1070.

[5]曾庆双,王茂,刘升才.三轴转台框架间动力学耦合及解耦研究[J].中国惯性技术学报,1997,5(3):44-49.

[6]辛哲奎,方勇纯,张雪波.小型无人机地面目标跟踪系统机载云台自适应跟踪控制[J].控制理论与应用，2010,27(8):1001-1006.

[7]孟恭.无人机视觉稳定云台系统设计[D]哈尔滨：哈尔滨工程大学，2011.

[8]郑翔,黄一,吕俊芳.机载光电跟瞄平台三轴环架模型的建[J].飞行设计,2003(4):41-45.

[9]REGINA,NIKI,ZANZI,et al.Camera pan-tilt gimbals robust control law for target tracking with fixed wing UAV,AIAA-2013-3816[R].Reston:AIAA,2013.

[10]KOLEV L,PETRAKIEVA S,MLADENOV V.Interval criterion for stability analysis of discrete-time neural networks with partial state saturation nonlinearities[C].Proceeding of the 7th Seminar on Neural Network Applications in Electrical Engineering,2004,2:11-16.

[11]SHIMEMURA E,FUJITA M.A design method for linear state feedback systems possessing integrity based on a solution of a Riccati-type equation[J].Int.J.Control,1985,42(4):887-899.

[12]YANG G H,WANG J L,YENG C S.Reliable guaranteed cost control for uncertain nonlinear systems[J].IEEE Trans.Automatic Control,2000,45(11):2188-2192.

[13]SINGH V.Improved criterion for global asymptotic stability of 2-D discrete systems with state saturation[J].IEEE Signal Processing Letters,2007,14(10):719-722.

[14]PATTON R J.Fault-tolerant control:the 1997 Situation[C].Proceedings of IFAC/IMACs Symposium on Fault Detection and Safety for Technical Process,Hull,England,1997,1033-1055.

[15]KAR H,SINGH V.Stability analysis of 2-D digital filters with saturation arithmetic:an LMI approach[J].IEEE Transactions on Signal Processing,2005,53(16):2267-2271.

(责任编辑：刘划英文审校：隋华)

UAV two-axis pan-title modeling and its adaptive fault-tolerant control

LIN Feng,WANG Xiao-xiao,QU Xiao-guang

(College of Automation,Shenyang Aerospace University,Shenyang 110136,China)

Abstract：Based on the kinematics and dynamics characteristics of UAV Two-axis Pan-title,the dynamic equations of two-axis platform were built.Moreover,the math model applicable to fault-tolerant controller design was built by predigesting and linearizing the model in the balance point.The adaptive fault-tolerant control method was used to design Two-axis Pan-title fault-tolerant controller,which could provide real time estimation of actuator faults.The adaptive fault-tolerant controller parameters could update automatically to compensate for the effects of fault on systems.The disturbance tolerance ability of the adaptive controller was higher than the fixed gain controller′s,especially in the case of actuator saturation and actuator failures.The proposed algorithm was calculated and simulated in the form of linear matrix inequalities with the aid of MATLAB LMI Control Toolbox.Results show that the controller has high disturbance tolerance ability,thus meeting the needs of stability and security control on UAV airborne system.

Key words：two-axis pan-title;modeling;linear matrix inequalities;adaptive control;saturation and failures

doi:10.3969/j.issn.2095-1248.2016.01.010

中图分类号：TP13

文献标志码：A

文章编号：2095-1248(2016)01-0047-07

作者简介：林峰(1963-)，男，辽宁沈阳人，教授，主要研究方向：控制理论与控制方向，E-mail:lfshenyang163@163.com。

收稿日期：2015-08-20