高中数学开放题编制的几点思考



高中数学开放题编制的几点思考

邵丽霞

(江苏省宜兴市和桥高级中学，214211)

开放题是一种十分重要的题目类型,它在高中数学教学中具有很好的教学功能．开放题之所以一直受到广大教师与命题者的青睐,是因为开放题当中包含了对学习效果的和能力的多方位考查．相比于传统形式的数学练习来讲,开放题从形式到内容都是相当灵活的,对其的解答需要从具体知识内容当中提炼出思想方法,以数学能力的方式加以运用．因此,能否巧妙应对开放题,可以作为评价学生数学能力的一个重要指标．如何恰到好处地编制开放题,也就成了每一个高中数学教师需要思考的重要问题．

一、由基础知识编制开放题

虽然开放题的解答对学生们的数学思维能力提出了较高的要求,但是,能力的产生与提升必然是从基础知识出发的．所以,教师在编制开放题时,绝不能一蹴而就,将注意力茫然地集中在思维能力上,而是要以公式定理等基础知识内容为依据,为学生提供一个思维能力不断提升的过程空间．

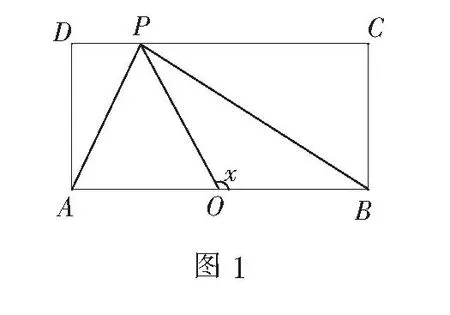
例如,在高三复习阶段,笔者以函数为主要内容,编制了这样一道开放题:如图1,长方形ABCD的边长BC长为1,AB长为2,点O 是AB边的中点．现有一动点P沿BC,CD,DA的顺序运动,设∠POB为x,以关于x的函数f(x)来表示点P到A、B两点的距离之和,则f(x)图象的大致形态是下列哪种?

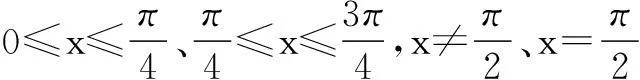
对基础知识的关注,为学生的思维提升搭建了一个方便上升的阶梯．基础知识的出现,让学生明确了解题所需思想方法的出处,无形当中为思考方向的确定提供了启示．另外,对基础知识的研究掌握,也是对接下来知识的深入研究提供的前提,只有具备了熟练的数学基础知识,才能在开放题思考中游刃有余．

二、以封闭试题为依据,引申编制开放题

对于高中教师来讲,开放题的编制不一定都是需要从零开始的,很多既有的封闭式题目都是极佳的基础素材,只要对之进行一定程度的巧妙改变,就可以得到十分理想的开放题．在很多情况下,看似与开放题毫无交集的封闭试题,恰好是开放题编制中十分重要的一个依据材料．当然,并不是每一种封闭性试题都可以被有效改变为开放试题的,这需要教师的仔细甄别与创新改变．

封闭性试题在高中数学当中的数量是很多的.对于很多基础性内容进行巩固离不开封闭试题的方式，而这也为开放题的编制提出了更多可能性．在实际教学过程当中,教师可以考虑将试题从封闭向开放转化的过程完整展现出来,先请学生们对知识本身进行封闭性思考,再随着一系列开放性问题的提出,将学生们的思维逐步打开,在循序渐进的思想阶梯当中实现数学能力的提升,这也就是我们所说的试题从封闭向开放的引申．

三、以思想方法为依据,提炼编制开放题

开放性试题对于很多高中学生来讲具有很大的挑战性.大家认为解答开放题的难度很大,不知道该如何寻找思维入口,感到解题思路总是处于变化当中,难以把握．这反映出了学生们在高中数学知识学习当中的一个共性的不足,即过于关注具体知识内容的学习,而缺乏对思想方法的整体性总结，这对于高中数学学习是十分不利的．因此,对于思想方法的强调,应当成为开放题编制的一个重要任务,将之进行提炼,并通过题目予以呈现．

例如,为了让学生们能够深刻体会数形结合的思想方法,我请学生们尝试解答这样一个问题:某个几何体的主视图、侧视图与俯视图如图2所示,能否求出该几何体的体积?这种提问方式,对于做惯了常规几何题型的学生来讲十分新颖．从题干当中并未明确给出太多已知条件,几乎全部需要学生通过观察来构造,开放性很强．想要顺利解答这个问题,数形结合思想的灵活运用必不可少,这也是我将这个问题呈现给学生的原因．在这道题的讲解中,我不仅引导学生运用空间想象能力还原几何体,还启发学生通过图中各边长度之间的关系来推测图形之间的相邻关系,数形结合,大大推进了题目解答．

思想方法的提炼,为开放题的解答提供了一个有效工具,也体现了开放题编制的一个重大价值．教师在编制开放题时,可以选择以所要应用到的思想方法来分类,让学生们在解答开放性问题时,对其中所包含的数学思想方法获得真切的感知,从而体会和掌握方法,站在一个更高的视角来理解知识,在开放题的推动下向更好的知识学习效果迈进．

四、以实际问题为依据,结合应用编制开放题

数学知识来源于生活,也应用于生活．因此,应用性是数学学科当中相当显著的一个特征,应当成为教师开展教学活动的一个重要侧重．与此同时,应用性的体现,也可以让学生们得到学以致用的知识学习体验,对激发学生学习热情很有好处．因此,教师在编制开放题时,加入实际应用的内容也就显得十分必要了．

例如,我曾经根据学生们在使用计算机时经常遇到的程序问题为依据,编制了这样一道开放题:某个计算机计算程序是依照我国古代数学名著《九章算术》当中所书的“更相减损术”设计出来的,其规则可以概括为如图3所示的框图．现输入a,b分别为14,18,则输出的a的值是多少?学生们在实际操作电脑时,经常会遇到输入某个数据,由电脑即时计算出相应结果的程序．这道开放题的背景,正好让学生们了解到了电脑背后的程序秘密,研究热情大增．以实际问题为依据所编制出的开放题,学生们非常乐于接受,相应的接受难度也降低了很多．

经过对多次实际教学过程的观察,笔者发现,以实际应用元素为内容的开放题,总能够更为顺利地激发学生们的探究热情．在这样的问题背景中,学生们找到了自身实际生活的影子,复杂灵活的数学问题对于学生来讲,自然没有那么陌生了．同时,在问题思考的过程中,学生们常常可以借助生活经验来启发思维,对于降低解题难度也具有一定帮助．这样的开放题编制方式,受到了学生们的普遍欢迎．

上述几种开放题的编制方法,比较全面地涵盖了高中数学教学的内容方向．虽然开放题对学生们提出了较高的能力要求,但这个能力的形成始终是要从基础出发建立的，因此,基本的概念、定理等内容必须成为开放题编制的出发点．这个坚实的基础夯实之后,方能对思想方法的抽象提炼,将学生们的数学思维引领到一个更高的层次水平．当然,在这过程中也要兼顾对数学应用特征的关注,它既是高中数学的重要属性,也是在开放题氛围当中非常容易实现的．有了明确的思路,相信高中数学教师在开放题编制过程中一定更为高效自如．