钢—混组合桁架节点处PBL剪力键群受力性能研究

王海波，杜元涛

(中南大学 土木工程学院， 湖南 长沙　410075)

近年来我国高速铁路、城市轨道交通快速发展，下承式钢—混组合桁架桥梁被广泛应用，西安—平凉铁路货运专线的太峪大桥、马屋泾河特大桥、后河村特大桥均采用了此类桥型。混凝土弦杆与钢腹杆的连接是该桥型的设计难点，连接的节点形式主要有整体耳板式、分离耳板式和外接式3种，且均采用PBL剪力键群传递内力。国内外学者已针对不同的实际工程进行了不同类型节点的模型试验[1-4]，系统研究其受力性能、破坏模式以及极限承载力，但由于结合段的剪力键分布密集且受力复杂，试验中对剪力键负载测试困难，导致对节点处PBL剪力键群受力性能的研究有所欠缺。

本文以广州至佛山城际铁路的1座50 m长钢—混组合桁架桥为背景，利用有限元分析软件ABAQUS建立3种类型节点的有限元模型，计算3级荷载作用下各剪力键的滑移量，通过单根PBL剪力键荷载—滑移关系反推其负载，进而分析节点处PBL剪力键群的负载分布规律及受力性能，并对其设计方法进行讨论。

1　单根PBL剪力键荷载—滑移关系的建立

PBL剪力键由混凝土榫、贯穿钢筋、开孔钢板组成。3种类型节点均采用Twin-PBL剪力键，即单根贯穿钢筋穿过2块开孔钢板。单向荷载作用下剪力键的变形如图1所示。已有理论和试验研究成果表明[5]，PBL剪力键通过钢构件与混凝土构件的相对滑移传递荷载。因此，较为准确地获得剪力键的滑移量是建立PBL剪力键荷载—滑移关系及研究剪力键群负载分布规律的关键，本文按下式计算滑移量

u=0.5(d端1-d孔1)+0.5(d端2-d孔2)

(1)

式中：u为PBL剪力键中心处钢构件相对于混凝土构件的滑移量；d端1，d端2，d孔1和d孔2分别为贯穿钢筋指定截面的绝对位移。

采用如下2种方法建立单根PBL剪力键的荷载—滑移关系。

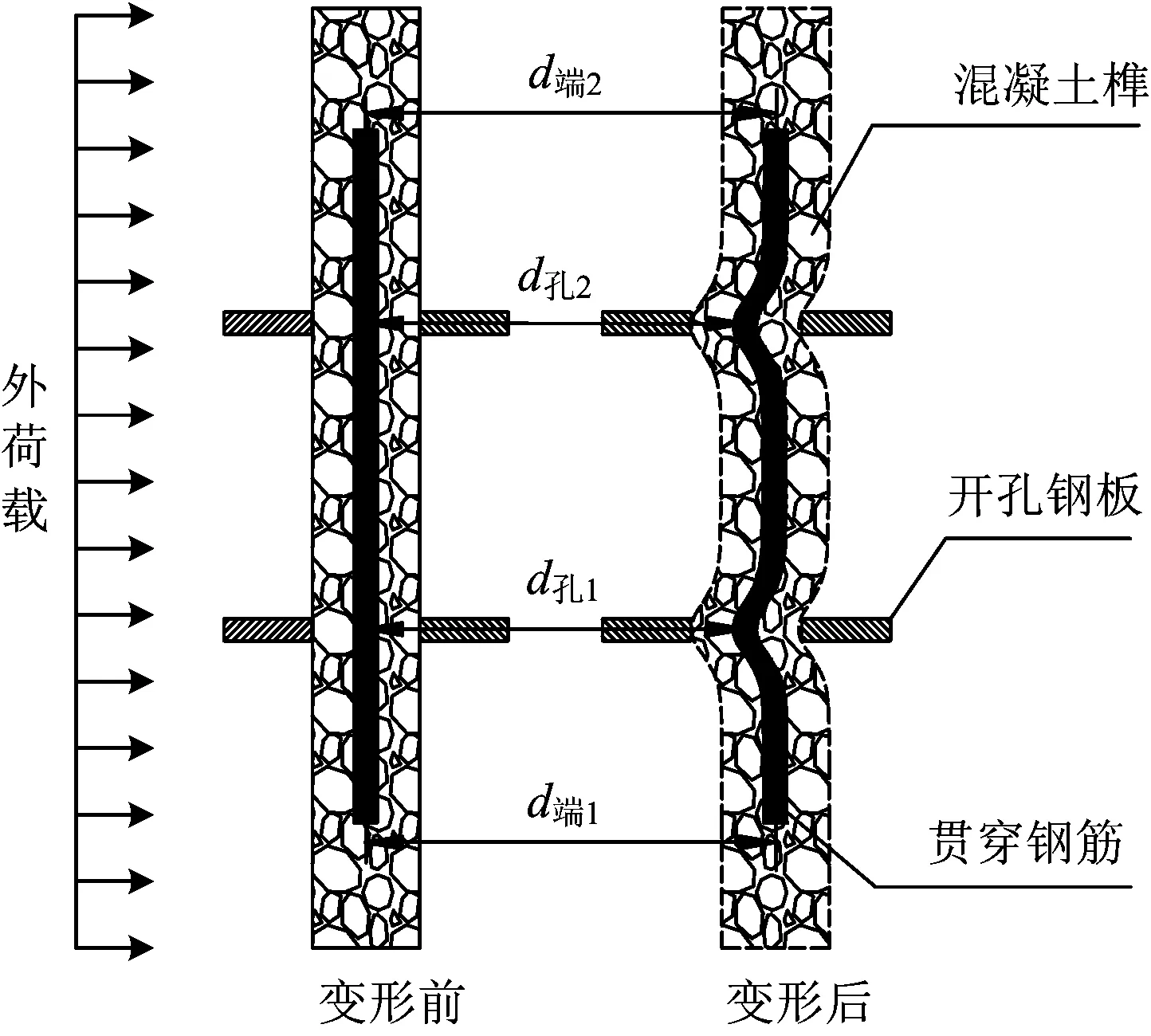
图1　单根PBL剪力键受力变形

1.1　公式法

试验研究表明[6-9]，单根PBL剪力键在加载初期，其荷载与滑移量大致呈线性关系；随荷载增加，曲线斜率缓慢变小，PBL剪力键表现出明显的非线性；继续加载，曲线斜率明显变小，极限荷载作用下剪力键的负载趋于极限承载力Pu。

学者汪维安等[9]借鉴学者Buttry[10]提出的栓钉荷载—滑移曲线，以南京长江三桥和四桥的12组42个试件试验数据为依据，经回归分析得到单根PBL剪力键的极限承载力计算式(2)，并给出了加载全过程的荷载—滑移关系式(3)，用单个函数表达式描述单根PBL剪力键加载的全过程。

(2)

(3)

式中：Ac为混凝土榫的截面面积；fc为混凝土抗压强度；Ad为贯穿钢筋截面面积；fy为贯穿钢筋屈服强度；Atr为箍筋截面面积；fs为箍筋屈服强度；D为钢板开孔孔径。

学者王振海[11]同样以南京长江三桥和四桥埋入式PBL剪力键的试验为基础得到了剪力键加载过程中各个阶段的荷载—滑移关系，其中弹性阶段计算式为

(4)

为弥补式(3)对剪力键弹性工作阶段描述的不足，本文对剪力键荷载—滑移关系的弹性工作阶段采用式(4)，塑性和强化阶段采用式(3)，弹性阶段的极限荷载Pk由式(3)与式(4)的交点得到，如图2所示。3种类型节点剪力键开孔孔径及贯穿钢筋直径以及依据上述方法计算得到的弹性极限荷载Pk、极限承载力Pu见表1。

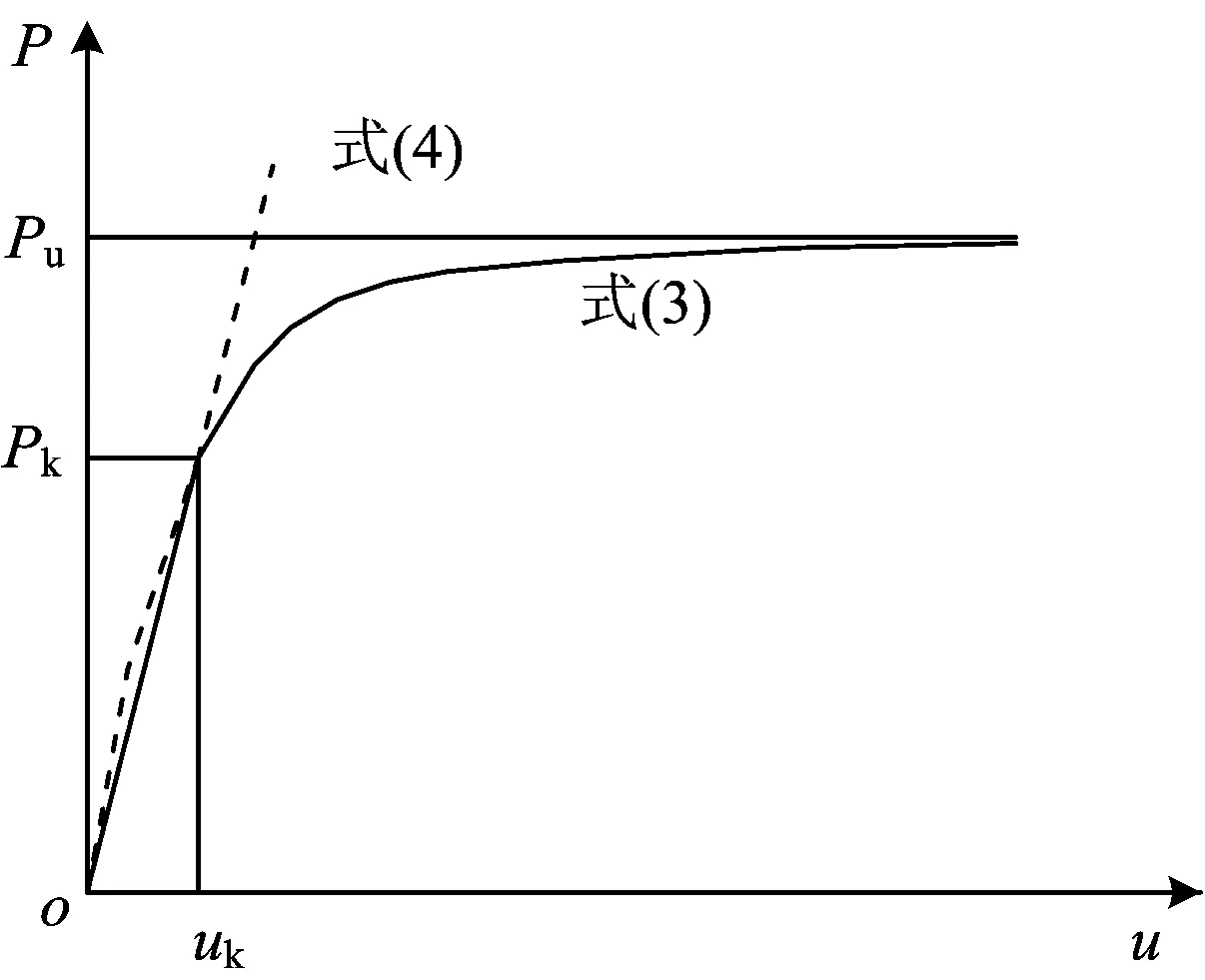
图2　3种类型单根PBL剪力键荷载—滑移曲线

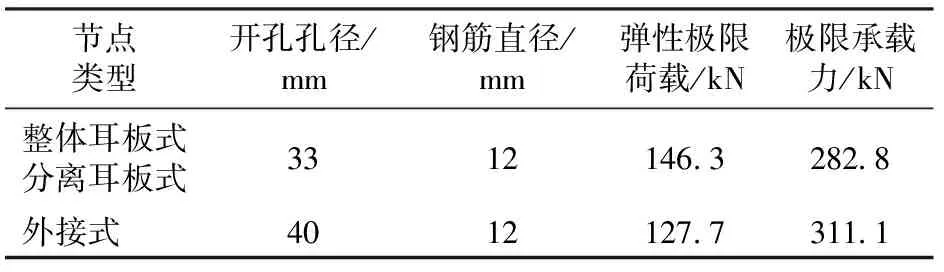
表1　剪力键的弹性极限荷载、极限承载力

1.2　有限元法

在计算参数取值合理的情况下，有限元仿真分析法能较为准确地模拟PBL剪力键在弹性、塑性阶段的力学行为。本文采用ABAQUS软件进行三维有限元分析，以获得单根PBL剪力键荷载—滑移关系。在建模过程中，将混凝土榫作为单独构件，既能突出混凝土榫对剪力键承载力提高的重要作用，又能方便局部网格增密；定义构件间相互作用时，开孔钢板圆孔与混凝土榫的接触面采用绑定约束，贯穿钢筋内置于混凝土榫中。

2　PBL剪力键负载的计算

2.1　组合桁架节点有限元模型建立

节点有限元模型依据文献[4]中试件尺寸建立，节点构造如图3所示，模型的力学计算简图如图4所示。钢—混结合段节点区视为刚性连接，A，B点为腹杆的反弯点，外荷载为节点两侧下弦杆轴力的差值。模型施加的荷载分为3个等级：1倍设计荷载(905 kN)、2倍设计荷载(1 810 kN)、3倍设计荷载(2 715 kN)。整体耳板式节点区域的三维模型、单行剪力键变形如图5所示。有限元模型中，混凝土采用实体单元模拟，其本构关系采用ABAQUS中提供的塑性损伤模型，混凝土的等效单轴应力—应变关系采用Hongestad公式计算，混凝土的强度等级为C55；贯通钢筋、钢板同样采用实体单元模拟，且均采用双折线本构模型，其初始弹性模量为210 GPa，屈服后弹性模量为21 GPa，钢板的屈服强度为335 MPa，钢筋的屈服强度为400 MPa。节点模型建立过程中同样引入混凝土榫，但建立相互作用时未将钢节点板内置在混凝土中，即水平力全部由PBL剪力键承担，各个剪力键承担的水平力之和应等于所施加的水平荷载，这种简化对于剪力键群的设计是偏于安全的。

图3　3种类型节点构造图(单位：mm)

图4　力学计算简图(单位：mm)

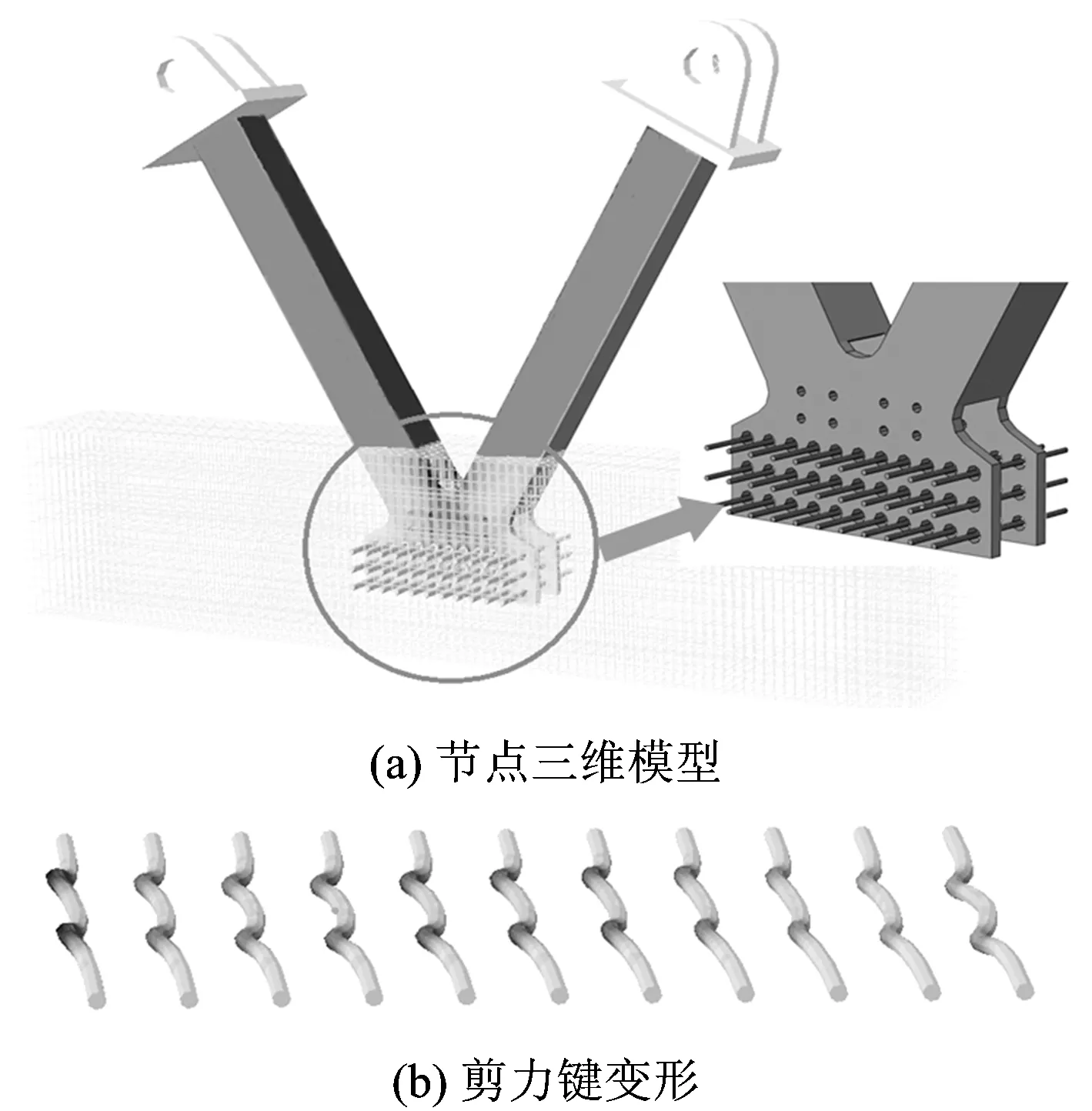
图5　整体耳板式节点的三维模型及PBL剪力键变形图

2.2　方法验证

以整体耳板式节点为例，分别采用上述2种方法计算剪力键的负载以验证计算方法的正确性。将PBL剪力键编号记为x-y，x为行编号，y为加载方向的列编号。运用有限元软件ABAQUS分别计算3级荷载作用下式(1)中各贯穿钢筋指定截面的绝对位移，进而得到剪力键的相对滑移，结果见表2。通过有限元法和公式法反推剪力键的负载结果见表3。

表2　3级荷载作用下PBL剪力键滑移计算结果　μm

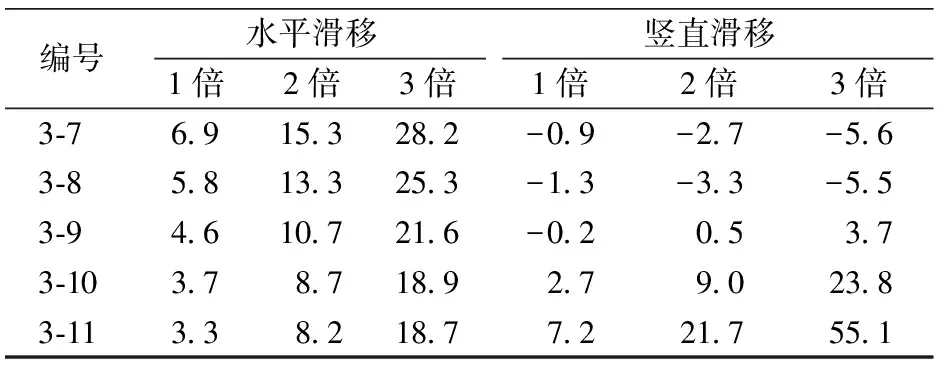
续表2

注：负号表示方向向下。

表4给出了有限元法与公式法计算结果的比值，可以看出有限元法与公式法计算的结果较为接近。 3个等级荷载作用下，水平向有限元方法计算的负载之和分别为1 036.0，1 869.1和2 777.5 kN，公式法计算的负载之和分别为915.7，1 915.7和2 879.4 kN，且2种方法计算的水平负载和与3个等级外荷载(905，1 810和2 715 kN)相近；竖向有限元方法计算的负载正值之和及负载负值之和分别为153.2和-169.9 kN，349.1和-374.1 kN，601.4和-616.3 kN，公式法计算的结果分别为120.0和-134.3 kN，296.5和-324.2 kN，612.4和-575.1 kN，负载的正值之和与负值之和相近，满足力学平衡条件。上述对比分析验证了2种方法的正确性。

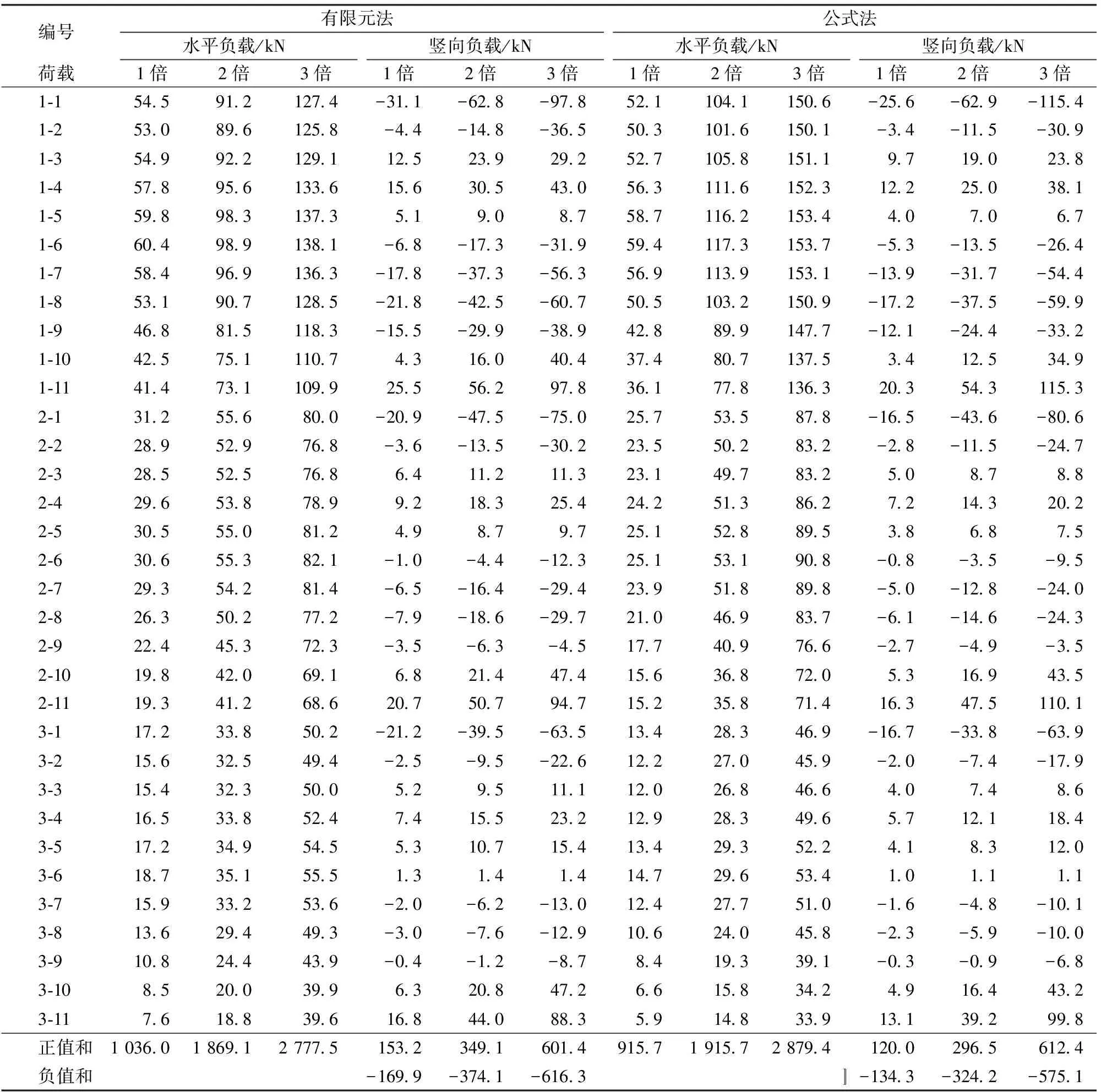
表3　3级荷载作用下PBL剪力键负载计算结果

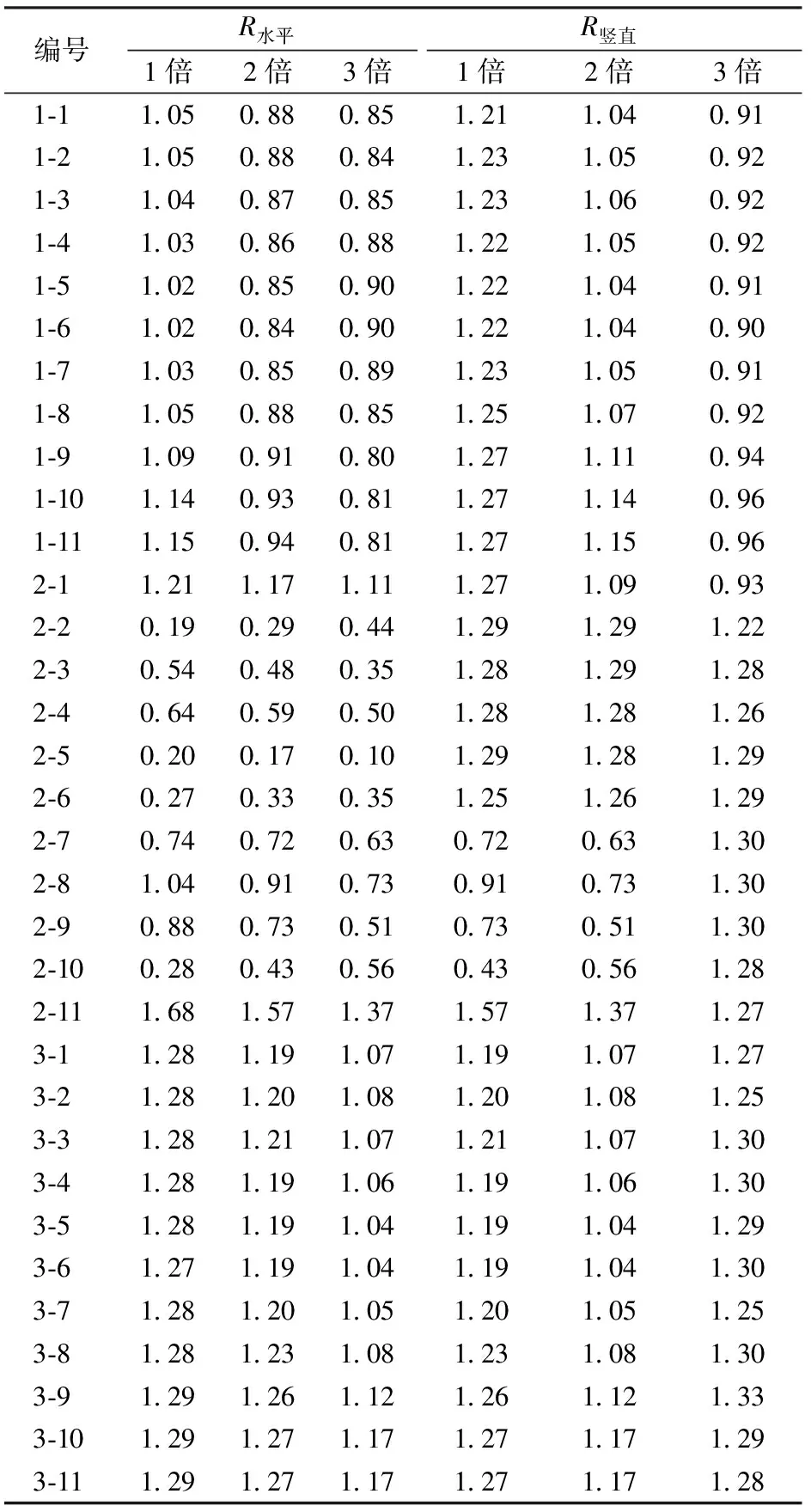
表4　有限元法与公式法计算的负载结果比值

2.3　PBL剪力键的负载分布

图6—图8给出了3种类型节点在3级荷载作用下的水平和竖向负载分布。各图的图(a)中各曲线上方的数字为各行剪力键负载的标准差，用于表征同行单侧剪力键水平负载的均匀程度。

可以看出：3种类型节点PBL剪力键的负载分布存在明显的共性。水平负载分布曲线呈“不平衡对称”模式，即靠近剪力键群竖向中心线附近的剪力键负载最大，向两侧呈递减趋势，近加载端一侧的负载总量高于远端；同列各行剪力键的负载由上而下逐渐减小；与荷载中心线最近或重合的一行剪力键的水平负载总量最大；整体耳板式节点和分离耳板式节点的均匀程度好于外接式节点；“不平衡对称”分布模式及荷载相对于剪力键群的偏心是导致剪力键群中各剪力键水平负载不均匀程度增加的主要原因，且后者影响显著；另外随荷载的增加，部分剪力键屈服后，荷载在剩余剪力键中进行了重分配，其最终结果为剪力键的负载趋于相对均匀，各剪力键的承载力利用更为充分，表现出良好的位移延性。

图6　整体耳板式节点PBL剪力键负载分布

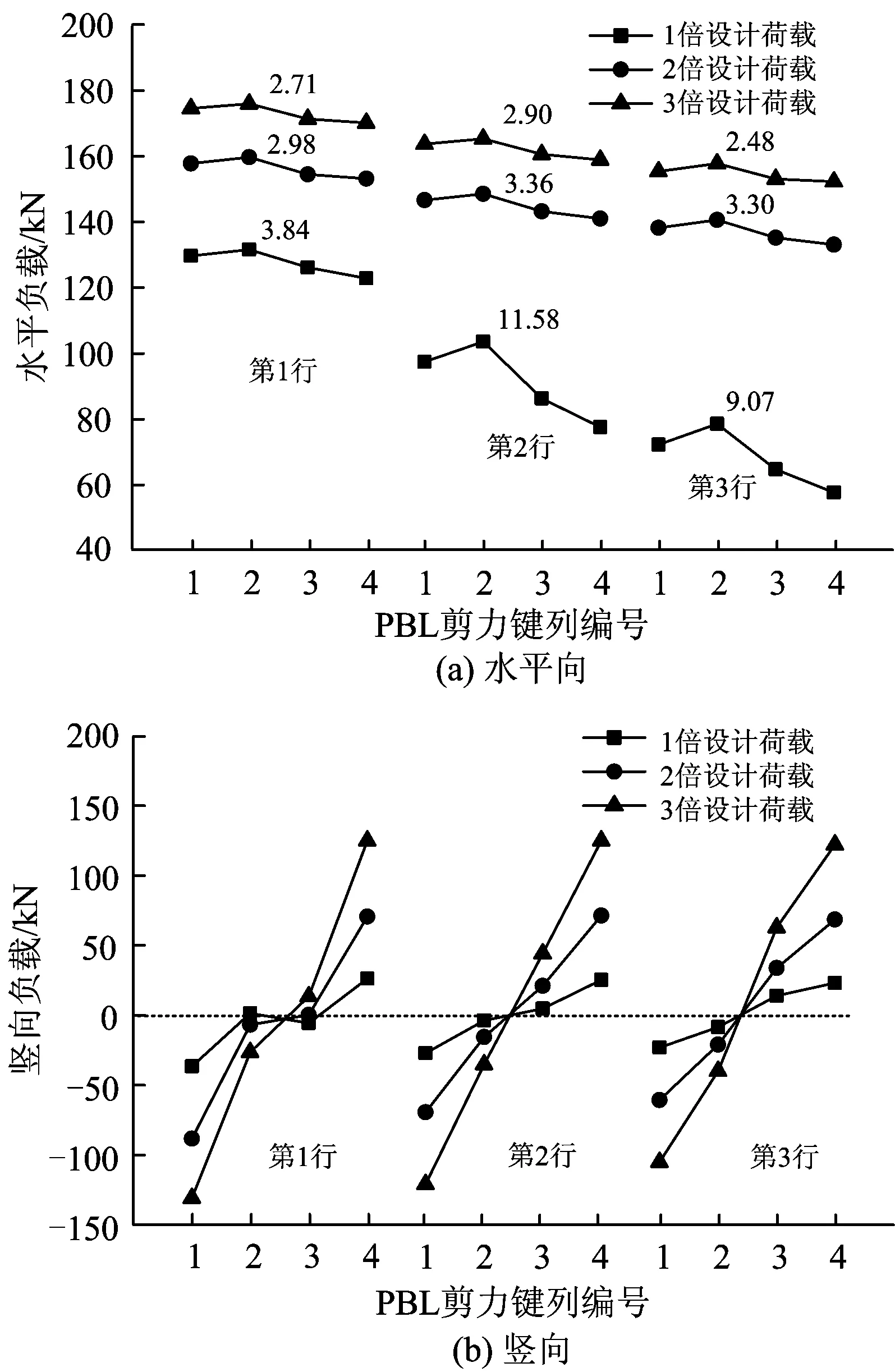
图7　分离耳板式节点PBL剪力键负载分布

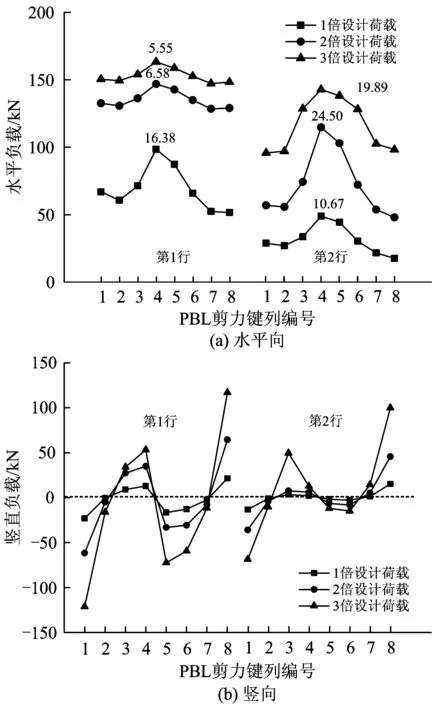
图8　外接式节点PBL剪力键负载分布

与水平负载相比，剪力键竖向负载较小，其分布曲线呈“反对称”模式，即以剪力键群的竖向中心线为对称轴呈反对称分布，宏观上表现为负载正值与负载负值总量相当；整体耳板式节点和分离耳板式节点中的剪力键群受拉压腹杆轴力的影响存在“异号影响区”，即受拉腹杆一侧剪力键竖向负载由正值过渡到负值，受压腹杆一侧由负值过渡到正值，分离耳板式节点由于剪力键布置向两侧分散，同侧竖向负载方向基本不发生改变；随荷载的增加，剪力键竖向负载分布的不均匀程度增加，但剪力键的负载方向基本保持不变。由图4计算得到的3级荷载作用下拉压腹杆轴力的竖向分量即剪力键群竖向荷载分别为814.5，1 629.1和2 443.6 kN，与计算的剪力键竖向负载总和相差较大，原因是拉压竖向载荷能够在剪力键上平衡，约占荷载总量的80%，未能在单根剪力键上平衡的荷载最终在剪力群中得到平衡。

3　节点处PBL剪力键群强度、疲劳性能校核方法讨论

列车进入桥跨结构时将引起其响应，节点处PBL剪力键承受的荷载方向、大小与列车在桥上行驶到的位置有关。在设计荷载作用下，剪力键群中各剪力键负载处于哪个工作阶段将影响其疲劳性能。本文基于剪力键的工作性质，提出组合桁架节点处PBL剪力键群强度和疲劳性能的校核方法。

1) 强度校核

剪力键群中单根剪力键负载最大值均应在极限承载力Pu以内。

2)疲劳性能校核

4　结　论

(1)本文基于有限元仿真分析方法计算得到钢—混组合桁架节点处PBL剪力键2个方向上的滑移分量，进而通过荷载—滑移曲线反推剪力键的负载量，并进行对比分析验证了方法的正确性。此方法同样适用于分析复杂荷载、复杂边界条件下组合结构PBL连接键群的负载分布、受力性能，弥补了现有试验方法对于复杂条件下PBL剪力键非单一方向负载测试的欠缺。

(2)钢—混组合桁架节点处PBL剪力键群的负载以水平方向为主，剪力键竖向负载较小，80%的竖向负载由单根剪力键的变形平衡承担，剩余部分以“反对称”模式分布在剪力键群中。随荷载增加，水平方向上，部分剪力键进入塑性阶段，荷载在各剪力键间重新分配，水平向负载最终趋于相对均匀，竖直方向上，剪力键负载较小，未进入塑性阶段，负载分布不均匀程度无明显变化。

(3)水平方向上，与荷载中心线最近或重合的一行剪力键负载总量最大，同行剪力键负载以加载侧总量最大，分布呈“不平衡对称”模式。在相同的荷载作用下，荷载中心线与PBL剪力键群中心线不重合是影响剪力键群水平向负载均匀程度的主要因素，在工程设计中，尽可能地将PBL剪力键群对称布置在弦杆中心线两侧，荷载中心线上不宜布置。

(4)依据工程要求，提出了组合桁架节点处PBL剪力键群强度和疲劳性能校核方法，并以此校核3种类型节点处PBL剪力键群的强度和疲劳性能，结果表明，3种节点方案的PBL剪力键群均能满足强度以及200万次以上疲劳寿命要求，强度储备方面，整体耳板式节点>外接式节点>分离耳板式节点。

(5)将混凝土榫作为一种构件应用在有限元模型的建立过程中，对于构件间相互作用定义更加准确，基本符合构件在实际结构中的工作状态。在网格划分时，便于对贯穿钢筋、混凝土榫等关键构件增密网格，避免了盲目减小网格尺寸导致的计算效率降低，计算结果更加精确。

[1]TAKASHI,KEISUKE F,YOUHEI.Development of a Panel Joint Structure for a Steel/Concrete Composite Truss Bridge-Test of Panel Joint Structure(the Steel Box Structure) on a Full-Sale Model[J].Annual Report of Kajima Institute,2002,50:25-32.

[2]TOSHIO N,SATORU O,TOSHIAKI K.Study on Strengthening Performance of Joints in PC Hybrid Truss Bridges (Part 2):Static Loading Test with 1/2-Scale Model Specimen[J].Obayashi Corporation Technical Research Report,2005,69:1-6.

[3]周凌宇,张花,贺桂超.耳板式钢—混凝土组合桁架节点力学性能试验研究[J].中国铁道科学,2011,32(6):41-47.

(ZHOU Lingyu,ZHANG Hua,HE Guichao.Experimental Research on the Mechanical Properties of the Steel-Concrete Composite Truss Joint with Ear Plate[J].China Railway Science,2011,32(6):41-47.in Chinese)

[4]王海波,尹国安,李一竹,等.外接式钢桁—槽型梁组合桁架节点模型试验研究[J].铁道科学与工程学报,2015, 12(2):323-329.

(WANG Haibo,YIN Guoan,LI Yizhu,et al.Experiment Study on External Steel Truss-Trough Girder Composite Truss Joints[J].Journal of Railway Science and Engineering,2015,12(2):323-329.in Chinese)

[5]汪维安,李乔,赵灿晖,等. 混合结构PBL剪力键群承载力试验研究[J]. 土木工程学报,2014,47(6):109-117.

(WANG Weian,LI Qiao,ZHAO Canhui,et al.Experimental Study on Bearing Capacity of PBL Shear Connector Group in Hybrid Structures[J].China Civil Engineering Journal,2014,47(6):109-117.in Chinese)

[6]LEONHARDT E F,ANDRAE W,ANDRAE H P,et al.Neues,Vorteilhaftes Verbundmittel fur Stahlverbundtragwerke Mithoher Dauerfestirkeit[J].Beton und Stahlbetonbau,1987,82(12):325-331.

[7]VELDANDA M R,HOSAIN M U.Behavior of Perfobond Rib Shear Connectors:Push-Out Tests[J] .Canadian Journal of Civil Engineering,1992,19(1):1-10.

[8]OGUEJIOFOR E C,HOSAIN M U.Numerical Analysis of Push-Out Specimens with Perfobond Rib Connectors[J].Computers & Structures,1997,62(4):617-624.

[9]王振海,赵灿晖,李乔. PBL剪力键荷载—滑移关系试验研究[J]. 西南交通大学学报, 2011, 46(4):547-552.

(WANG Zhenhai, ZHAO Canhui, LI Qiao. Experimental Investigation on Load-Slip Relationship of Perfobond Rib Shear Connectors [J]. Journal of Southwest Jiaotong University, 2011, 46(4):547-552.in Chinese)

[10]OLLGARRD J G, SLUTTER R G,FISHER J W.Shear Strength of Stud Connectors in Lightweight and Normal-Weight Concrete [J] ASIC Engineering Journal,1971,8(2):55-64.

[11]王振海. 埋入式PBL剪力连接件力学特性及承载机理研究[D].成都：西南交通大学,2012.

(WANG Zhenhai.Study on Mechanical Property and Load-Bearing Mechanism of Embedded Perfobond Rib Shear Connectors [D].Chengdu: Southwest Jiaotong University,2012.in Chinese)

[12]卫星,肖林,邵柯夫,等.钢—混组合结构PBL剪力键疲劳寿命试验[J].中国公路学报, 2013, 26(6):96-102.

(WEI Xing,XIAO Lin,SHAO Kefu,et al.Fatigue Performance of Perfobond Shear Connector in Steel-Concrete Composite Structure[J]. China Journal of Highway and Transport,2013,26(6):96-102.in Chinese)