飞机简化模型水上迫降入水的数值研究

王丑丑，吴宗成

(北京航空航天大学 航空科学与工程学院，北京　100191)



飞机简化模型水上迫降入水的数值研究

王丑丑，吴宗成

(北京航空航天大学 航空科学与工程学院，北京100191)

摘要：在飞机水上迫降过程中，其尾部吸力对姿态角的变化具有重要影响。基于Fluent软件，利用动网格技术、用户自定义函数(UDF)、六自由度(6DOF)模型、流体体积(VOF)模型，首先对二维圆柱、三维椭圆抛物体垂直入水以及三维平板水平划水进行数值模拟，并与试验结果对比验证模拟方法的可靠性；然后对NACA TN 2929简化飞机模型进行水上迫降数值模拟。研究发现：尾部吸力使飞机俯仰姿态角发生剧烈变化，入水初期尾部吸力产生的抬头力矩使飞机姿态角快速增加，当姿态角达到最大时，尾部吸力产生的抬头力矩很小，在重力作用下飞机姿态角快速减小。本文所采用的三维数值模拟方法能够较好地模拟飞机水上迫降过程中的吸力和姿态角变化。

关键词：飞机简化模型；水上迫降；数值模拟；动网格；吸力；姿态角

0引言

随着经济全球化的发展，跨海航线逐渐增多，飞机发生水上迫降的几率也逐渐增大。飞机一旦发生水上迫降事故，可能会造成机毁人亡的严重后果，因此，世界各国在制定民用运输机适航条例时，把水上迫降性能验证作为适航认证的一个重要方面。我国民用飞机适航条例CCAR-25部，就民用飞机的水上迫降合格审定作了明文规定[1]，要求必须通过模型试验，或与已知水上迫降性能构型相似的飞机进行比较，以检查飞机的水上迫降性能。

理论研究方面，最早可追溯到1929年Von Karman Th[2]根据动量守恒原理和附加质量法对水上飞机降落时浮筒冲击载荷的研究。1932年，H.Wagner[3]将Von Karman Th的方法理论化，并考虑了冲击时水面的抬升现象。基于上述理论，许多学者相继提出了一些改进。然而，水上迫降过程的理论分析涉及水表面边界形状的改变，是一个高度非线性的问题[4]，对物理模型进行理论分析难度很大，进展缓慢。

试验研究方面，美国已经进行了数十种机型的动力模型水上迫降试验，积累了大量研究成果。波音公司在多种型号喷气式民航飞机的水上迫降适航鉴定时，主要依托积累的试验结果，来外推评估其系列飞机的水上迫降性能。麦道公司在DC-9和DC-10的研制初期，进行了模型水上迫降试验，以研究其水上迫降性能。空中客车公司在A300的研制初期也曾进行模型试验，现已改用分析法确定飞机的水上迫降性能[4]。20世纪90年代，我国进行了新舟60的水上迫降试验。中国商用飞机有限责任公司研制生产的ARJ21-700飞机模型也进行过拖拽水池试验及开阔水面模型试验[5]。系统地进行重点型号飞机的水上迫降模型试验，对我国原始数据的积累很有必要。

与水上迫降缩比模型试验相比，数值模拟方法的成本更低廉，且灵活方便，该方法不仅可以给出相关的冲击载荷，还可以详细地展示流场结构，为深入分析问题提供参考。入水冲击问题的数值模拟方法主要包括边界元法、有限元法、光滑粒子水动力学法和有限体积法等[6]。在水上迫降过程中，尾部吸力的作用是研究的难点之一[7]，有限元法和光滑粒子水动力学法可以较好地模拟冲击特征，但对吸力及其相关力学行为的模拟有所欠缺；有限体积法结合流体体积(VOF)模型通常可以较好地模拟上述问题。

目前，我国ARJ21-700飞机正在进行适航取证，C919飞机即将进行首飞，未来还会研制宽体客机。为了加快适航取证进程，在型号设计中必须考虑相关适航要求，水上迫降作为适航取证的重要组成部分，对其数值模拟方法进行研究十分重要。

本文基于有限体积法，利用 Fluent 15.0流体计算软件，使用动网格技术、用户自定义函数、六自由度模型、流体体积模型，首先对二维圆柱自由及定速入水进行数值模拟，对其冲击力系数、压强分布以及水气交界面形状等进行对比分析；然后对三维椭圆抛物体定速入水、三维平板划水进行模拟，并和相关试验结果进行对比，以验证三维模拟方法的可靠性；最后对NACA TN 2929飞机模型进行模拟，将计算结果和相关试验结果进行对比分析。

1数值方法

使用ICEM CFD 15.0建立计算模型并进行网格划分，将计算域分为动网格区和变形网格区，使用动网格技术模拟物体相对水面的运动，采用VOF模型捕捉自由液面的变形。物体假定为刚体，忽略表面张力，考虑重力影响。控制方程为非定常雷诺时均Navier-Stokes方程，湍流模型为标准k-ε湍流模型。对于二维模拟，压力与速度耦合采用PISO算法，水气体积分数采用Geo-Reconstruct格式；对于三维模拟，压力与速度耦合采用SIMPLEC算法，水气体积分数采用Modified-HRIC格式。对于定速入水或划水运动，使用Profile文件控制运动轨迹；对于自由落水或水上迫降运动，使用UDF和6DOF控制其运动状态。本文所述压强均为相对压强，正压表示压强值高于大气压强，负压表示压强值低于大气压强。

2圆柱入水数值模拟

2.1圆柱自由入水数值模拟

参考M.C.Lin等[8]的几何数据，使用ICEM CFD 15.0建立计算模型，进行二维圆柱自由落水数值研究。圆柱直径为0.2 m，计算过程中对圆心角θ分别为 0°、7.5°、15°和30°位置的压强变化进行监测，如图1所示。初始时圆柱底部位于水面以上0.03 m处，理论入水速度为0.766 8 m/s，试验模型厚度为0.2 m，质量为12.5 kg，则单位长度试验模型质量为62.5 kg。

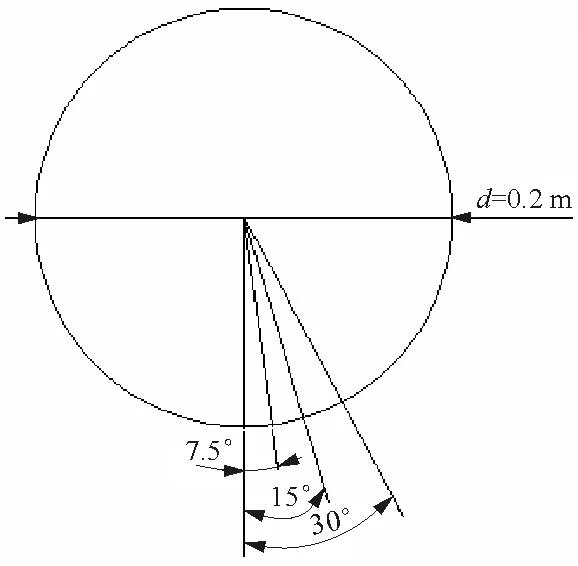
图1　压力计位置

计算域高2.5 m，宽2.0 m，初始时圆柱中心距离计算域顶部1.0 m，如图2所示。两圆之间的环形区域为动网格区，动网格区外为变形网格区，为了保证计算过程中圆柱附近的网格质量，使动网格区随圆柱一起运动，变形网格区进行网格重构。为了更好地模拟圆柱运动过程中的受力、压强分布以及水气交界面形状等，在圆柱壁面外厚度约0.018 m的圆环区域内划分结构网格，计算域中其他区域划分非结构网格。将计算域上方设置为压力出口边界条件，左右两侧及下方设置为固壁边界条件。计算过程中，通过UDF和6DOF控制圆柱运动，计算开始后，圆柱将由静止开始自由下落。

图2　计算域示意图(圆柱自由入水)

为了确定网格尺寸对数值模拟结果的影响，选取三种不同尺寸的网格进行对比研究，壁面处首层网格高度分别为0.000 4、0.000 2和0.000 1 m，结构网格区厚度约为0.018 m，动网格区最大网格尺寸分别为0.016、0.008和0.004 m，全局最大网格尺寸分别为0.08、0.04和0.02 m，时间步长均为0.000 05 s。网格尺寸如表1所示。

表1　网格尺寸

圆柱自由入水的冲击力系数(Cf)计算公式为

Cf=F/ρv2R

(1)

式中：F为圆柱入水过程中受到水的冲击力；ρ为水密度；v为圆柱底部初始触水时的入水速度；R为圆柱半径。

圆柱自由入水的冲击力系数随相对入水深度(Vt/R)的变化曲线如图3所示。

(a) 冲击力系数

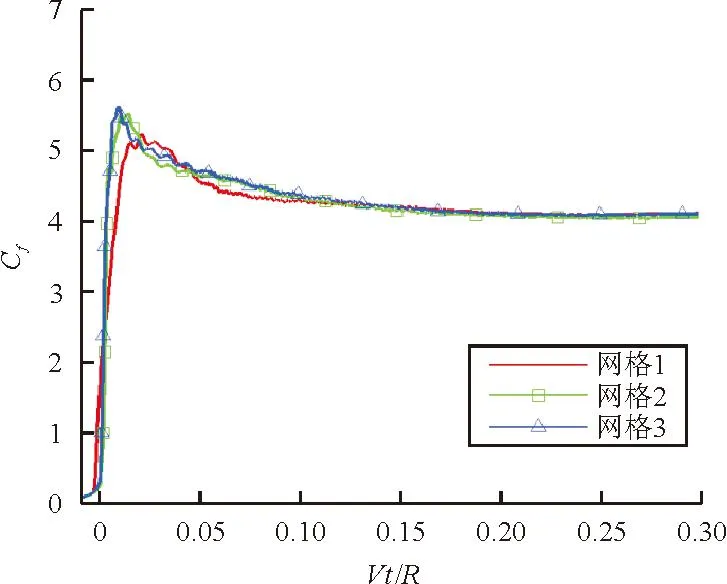
(b) 冲击力系数光顺图

从图3(a)可以看出：冲击力系数在峰值附近波动较大；对图3(a)进行光顺处理，得到图3(b)，从图3(b)可以看出：入水后冲击力系数快速达到最大值，然后开始缓慢下降，网格2、网格3的模拟冲击力系数变化趋势基本相同，在峰值之后略有不同，网格1与网格2、网格3的模拟结果相比，在峰值附近差异略大。

压强系数(Cp)的计算公式为

Cp=(p-pref)/(0.5ρv2)

(2)

式中：p为静压；pref为参考压强。

三种不同网格尺寸模拟压强系数随时间的变化曲线与试验结果的对比如图4所示。

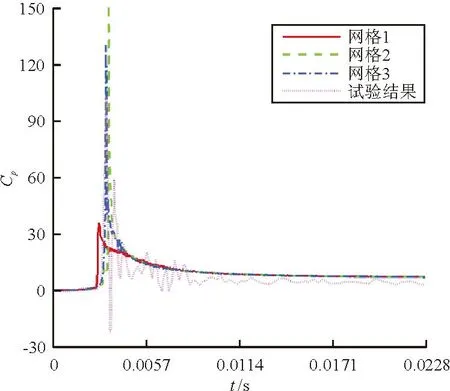
(a) 0°位置

(b) 7.5°位置

(c) 15°位置

(d) 30°位置

从图4可以看出：随着圆心角的增大，冲击力压强系数峰值逐渐减小；网格2、网格3的模拟压强系数在四个压强监测点处均比较接近，只在0°位置处最大压强系数略有不同；网格1的模拟压强系数，在0°位置的变化趋势以及0°和7.5°位置的最大压强系数与网格2、网格3差别较大；在0°和7.5°位置，三种网格模拟压强系数峰值均在试验压强系数峰值附近波动，15°和30°位置的模拟压强系数峰值和试验结果十分接近；网格2、网格3的模拟结果变化趋势与试验结果吻合较好，表明网格2的模拟结果已经能够满足精度要求。

当Vt/R=0.18时，三种不同网格模拟的圆柱附近水气交界面形状如图5所示。

(a) 网格1

(b) 网格2

(c) 网格3

从图5可以看出：三种网格模拟的水气交界面形状比较接近，但沿圆柱两侧表面向上流动的贴体流分离情况略有不同，网格2、网格3对贴体流的流动分离情况模拟得比较清晰。

当时间分别为0.011 4、0.022 8、0.034 2、0.045 6 s时，网格2模拟的水气交界面形状如图6所示。

(a) t =0.011 4 s

(b) t =0.022 8 s

(c) t =0.034 2 s

(d) t =0.045 6 s

从图6可以看出：当圆柱底部刚接触水面时，圆柱底部流体由于受到圆柱挤压沿着圆柱底部表面向两侧流动，随着圆柱继续向下运动，受到挤压的流体继续沿着圆柱表面进行贴体流动，随着圆柱入水深度的进一步增加，沿圆柱表面运动的流体在运动到一定位置后开始发生分离，网格2较为明显地模拟出了分离和水面的抬升现象。

圆柱触水后网格2的模拟速度与试验速度的对比如图7所示。

图7　模拟速度和试验速度对比

从图7可以看出：模拟速度和试验速度吻合较好。由于圆柱初始下落高度较小，初始触水速度较小，当圆柱触水后，冲击力小于重力，速度继续增加。

2.2圆柱定速入水数值模拟

选取半径R1=0.104 8 m的圆柱为研究对象，使用ICEM CFD 15.0建立计算模型，进行二维圆柱定速入水数值研究。计算域中，除模型半径R1不同外，其他均与图2相同。网格划分也与圆柱自由入水类似，将壁面附近划分为结构网格，其余部分均划分为非结构网格，网格总数为95 768。将计算域上方设置为压力出口边界条件，左右两侧及下方设置为固壁边界条件。通过profile文件控制物体运动，初始时，圆柱最低点位于水面以上0.023 3 m，然后以2.33 m/s的速度做垂直向下的定速运动。

圆柱入水过程中冲击力系数随相对入水深度的变化曲线如图8所示。

图8　冲击力系数对比图(圆柱定速入水)

从图 8可以看出：模拟结果与R.Cointe[9]v=2.33 m/s的试验结果吻合较好，只在峰值附近略有不同，高于Mei Xiaoming等[10]附加质量的理论分析结果。

通过对二维圆柱自由以及定速入水进行数值模拟可知，该二维数值模拟方法能够对圆柱入水过程中的冲击力系数、压强以及水面变化等进行较好的模拟。网格2对四个压强监测点处压强系数随时间变化总体趋势模拟较好，模拟压强系数大小和试验结果比较接近，能够满足精度要求。小圆心角压强与试验差异略大，此时当地抬升角很小，压强很大，对模拟和试验要求都很高。

3椭圆抛物体垂直入水数值模拟

参考A.Tassin等[11]的几何数据，使用ICEM CFD 15.0建立椭圆抛物体计算模型(如图9所示)，进行椭圆抛物体定速入水数值研究。模型上表面为椭圆，其长轴为0.53 m，短轴为0.32 m，面积为0.133 m2，柱体部分高0.03 m；下表面为椭圆抛物面，其曲面方程为

f(x,y)=a×x2+b×y2

(3)

式中：a=1.418；b=0.517。坐标原点位于椭圆抛物面最低点。

计算域的长、宽、高分别为3.0、3.0和3.5 m，如图10所示，椭球内为动网格区，椭球外为变形网格区。为了保证壁面附近的网格质量，在物体表面附近设置密度核；为了更好地模拟物体入水过程中的受力情况，在壁面附近设置prism边界层网格，其他均采用非结构网格，网格总数为848万。将计算域上方设置为压力出口边界条件，前后左右及下方设置为固壁边界条件。通过profile文件控制物体运动，初始时，计算模型最低点位于水面以上0.05 m处，然后以10 m/s的速度做垂直向下的定速运动。

图9　椭圆抛物体计算模型

图10　计算域示意图(椭圆抛物体垂直入水)

椭圆抛物体垂直入水的冲击力系数(Cs)计算公式为

Cs=2F/ρv2Smax

(4)

式中：F为垂直方向受到水的冲击力；v为垂直向下运动的速度；Smax为椭圆抛物体在垂直方向投影面积的最大值，其值为0.133 m2。

椭圆抛物体垂直入水的冲击力系数与试验结果的对比如图11所示。

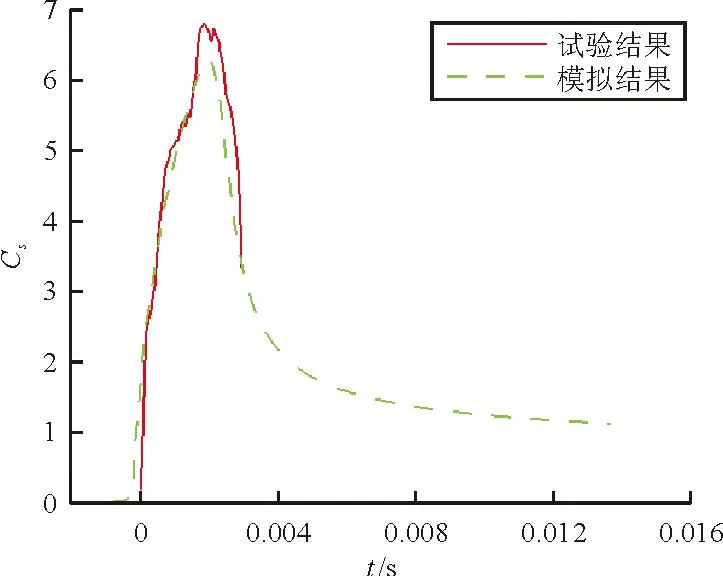
图11　试验和模拟冲击力系数对比

从图11可以看出：椭圆抛物体底部刚触水时，冲击力系数几乎为0，随着入水深度的增加，冲击力系数快速增加，达到最大值后开始快速下降；模拟冲击力系数与试验结果变化趋势吻合较好，数值也十分接近，模拟最大冲击力系数比试验结果略小。

入水时间分别为0.000 5、0.001 5、0.002 5和0.003 0 s时，椭圆抛物体纵向对称截面压强系数对比如图12所示，图中纵坐标x/L表示纵向对称截面相对坐标。

图12　纵向对称截面压强系数对比

从图12可以看出：随着入水深度的增加，压强系数逐渐减小，压强系数峰值同时减小；在入水0.002 5 s时，物体入水0.025 m，在静水中对称截面底部两侧仍未触水，而对称截面底部两侧已受到较大的冲击压强作用，这是由于水面抬升喷溅造成的；在入水0.003 0 s时，物体已入水0.030 m，由于物体运动过程中水面发生抬升，此时椭圆抛物体底部已经全部入水，压强系数较为平缓。

4三维平板划水数值模拟

参考W.Sottorf[12]的8°攻角平板划水试验，使用ICEM CFD 15.0建立计算模型，进行三维平板划水数值模拟，平板纵向对称截面尺寸如图13所示，平板长度为0.525 m，厚度为0.010 m，宽度为0.300 m，与水平面的夹角为8°，当水面静止时，平板下表面浸水长度为0.175 m。

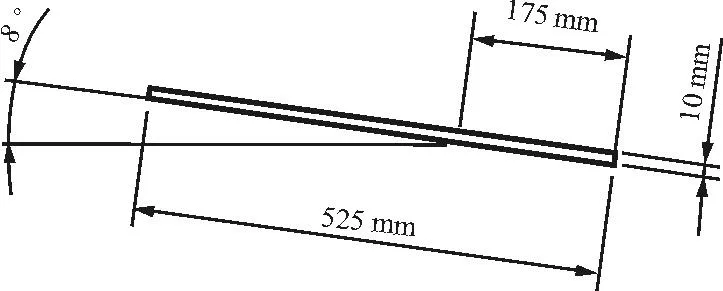
图13　平板纵向对称截面尺寸示意图

计算域的长、宽、高分别为3.5、2.0和1.0 m，动网格区长、宽、高分别为0.9、0.9和0.2 m，如图14所示，全部采用非结构网格，网格总数为940万。将计算域上方设置为压力出口边界条件，前后左右及下方设置为固壁边界条件。通过profile文件控制平板水平运动，水平向左划水速度为6 m/s。

图14　计算域示意图(三维平板划水)

平板纵向对称面上的压强分布与试验结果的对比如图15所示。

图15　模拟压强与试验结果对比

从图15可以看出：最大压强点及该点之后的压强变化，模拟结果与试验结果十分接近，而在最大压强点之前，试验压强结果上升更快。

平板下表面中线处以及距离中线不同距离处的压强分布对比如图16所示。

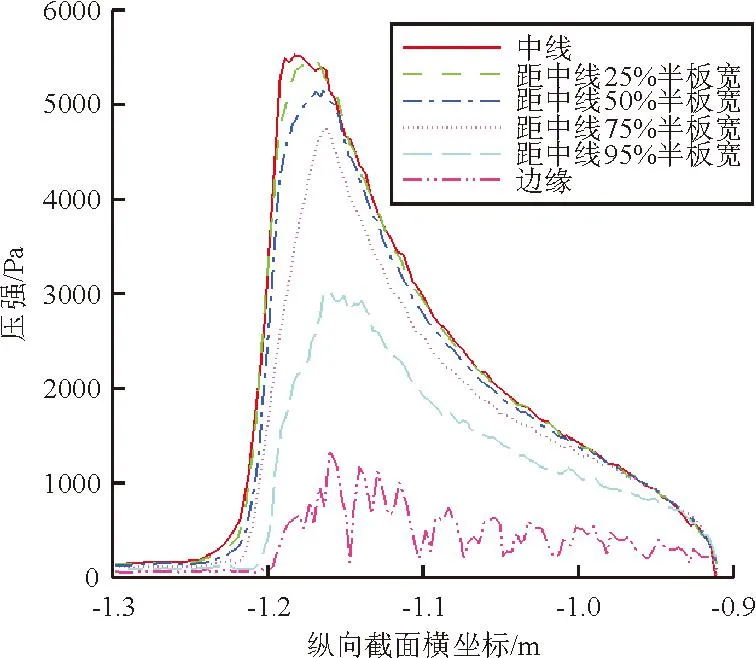
图16　不同纵向截面的压强对比

从图16可以看出：平板中线处压强最大，随着距离中线距离的增加，压强逐渐减小；图中每一条曲线的压强分布趋势基本相同，先快速增加，在最大压强点处之后逐渐减小，在平板末端基本减小为大气压强。

平板纵向对称面附近的水气交界面形状如图17所示，数值模拟中该位置板的浸湿长度为0.292 m，试验结果为0.245 m，模拟结果比试验结果偏大约19%。

图17　纵向对称面水气交界面形状

通过对三维椭圆抛物体垂直入水以及三维平板划水进行数值模拟可知，该三维数值模拟方法能够对三维物体运动过程中的冲击力系数、压强及水面变化进行较好的模拟，表明该方法是可靠的。

5飞机简化模型水上迫降数值模拟

参考E.E.Mcbride等[13]的NACA TN 2929飞机模型A，使用ICEM CFD 15.0建立飞机模型，如图18所示。试验模型尾部结构与机身连接较弱，受到水载荷作用时会脱落，因此在建模时不考虑平尾和立尾。机身中心线为直线，长为1.219 2 m，长细比为6，翼展为1.676 4 m，翼根处采用NACA 23015翼型，翼尖处采用NACA 23009翼型，梢根比为0.455，整个模型重5.67 kg。

图18　简化飞机模型

计算域的长、宽、高分别为13.0、9.0和6.5 m，球形动网格区半径为1.5 m，如图 19所示，全部采用非结构网格，网格总数为855万。将计算域上方设置为压力出口边界条件，前后左右及下方设置为固壁边界条件。使用UDF和6DOF控制飞机运动，限制其展向运动、偏航运动以及滚转运动。飞机初始运动时，机身中心线与水面的夹角为10°，机身最低点基本与水面接触，初始水平运动速度为9.144 m/s，垂直运动速度为0.2 m/s。飞机在重力、气动力、水载荷的共同作用下在纵向对称面内做三自由度平面运动。

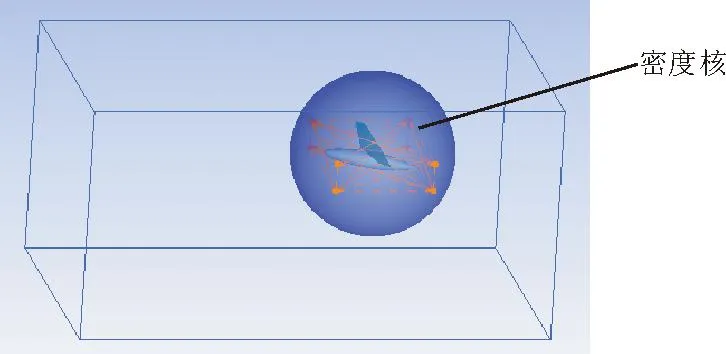
图19　计算域示意图(模型飞机水上迫降)

模拟姿态角与试验结果、H.Streckwall等[14]的模拟结果的对比如图20所示。

图20　姿态角对比

从图20可以看出：本文模拟结果低于试验结果，而与文献[14]的模拟结果相比，本文结果高于DITCH模拟结果、低于COMET模拟结果，介于二者之间。

当时间分别为0.038 4、0.073 4、0.183 4和0.343 4 s时，模型飞机机身底部的压强云图如图21所示。

(a) t=0.038 4 s

(b) t=0.073 4 s

(c) t=0.183 4 s

(d) t=0.343 4 s

从图21(a)可以看出：当机身后部刚接触水面时，由于受到水的冲击作用而产生低头力矩，飞机进行低头运动；随着飞机向下运动，飞机底部触水面积逐渐增加，机身底部同时存在正压区和负压区，飞机由于受到尾部负压作用，低头力矩减小，逐渐变为抬头力矩，低头速度逐渐减小。

从图21(b)可以看出：随着运动的继续，正压区和负压区均逐渐增大，且由于入水深度增加，正压区逐渐前移，抬头力矩继续增大，飞机已开始做抬头运动。

从图21(c)可以看出：随着姿态角不断增大，飞机最低点移至机身末端，负压区逐渐向机身尾部两侧移动，导致抬头力矩减小并逐渐变为低头力矩，抬头速度达到最大。

从图21(d)可以看出：在低头力矩作用下，飞机抬头速度逐渐减小为0，飞机此后将做低头运动。

综上所述，飞机刚触水时，水的冲击作用使飞机发生低头运动，随着运动的继续，机身尾部产生的吸力使其俯仰姿态角快速增加，当姿态角较大时，随着姿态角增加，吸力逐渐向机身尾部两侧移动，吸力产生的抬头力矩逐渐减小，当姿态角达到最大时，尾部吸力产生的抬头力矩已经很小，飞机在重力等作用下姿态角开始快速减小；本文采用的数值模拟方法能够对模型飞机水上迫降过程中的姿态角以及尾部吸力进行较好模拟。

6结论

(1) 对二维圆柱、三维椭圆抛物体垂直入水以及三维平板水平划水进行数值模拟，将模拟结果和试验结果进行对比可知两者吻合较好，表明本文采用的数值模拟方法是可靠且有效的。

(2) 尾部吸力使得飞机水上迫降过程中姿态角发生剧烈变化，在入水前期，尾部吸力的存在使飞机俯仰姿态角快速增加，当姿态角达到最大后，尾部吸力向机身尾部两侧移动，其产生的抬头力矩很小，在重力作用下飞机姿态角快速减小。

(3) 本文所采用的数值模拟方法能够对飞机水上迫降过程中的吸力以及姿态角变化进行较好的模拟。

参考文献

[1] 中国民用航空局. CCAR-25-R4运输类飞机适航标准[S]. 北京: 中国民用航空局, 2011.

Civil Aviation Administration of China. CCAR-25-R4 Airworthiness standards: transport category airplanes[S]. Beijing: CAAC, 2011.(in Chinese)

[2] Von Karman Th. The impact on seaplane floats during lan-ding[R]. Technical Report Archive & Image Library NACA TN 321, 1929.

[3] Wagner H. Phenomena associated with impacts and sliding on liquid surfaces[J]. Math Mech, 1932, 12(4): 193-215.

[4] 李斌, 杨智春. 大型运输机水上迫降研究进展[C]. 中国航空学会2007年学术年会, 2007.

Li Bin, Yang Zhichun. The ditching research progress of large transport[C]. 2007 Annual Academic Conference of Chinese Society of Aeronautics and Astronautics, 2007.(in Chinese)

[5] 郭保东. 民用运输机水上迫降力学性能数值研究[D]. 北京: 北京航空航天大学, 2013.

Guo Baodong. Numerical study on the hydrodynamic characteristics of civil transport in ditching[D]. Beijing: Beihang University, 2013.(in Chinese)

[6] 刘沛清, 屈秋林, 郭保东, 等. 数值计算技术在飞机水上迫降中的应用[J]. 力学与实践, 2014, 36(3): 278-284.

Liu Peiqing, Qu Qiulin, Guo Baodong, et al. Application of computational fluid dynamics in the planned ditching of a transport aircraft[J]. Mechanics in Engineering, 2014, 36(3): 278-284.(in Chinese)

[7] 张韬, 李书, 代恒超. 大型客机水上迫降尾部吸力效应分析[J]. 中国科学: 技术科学, 2012, 42(12): 1407-1415.

Zhang Tao, Li Shu, Dai Hengchao. The suction force effect analysis of large civil aircraft ditching[J]. Science China Technological Sciences, 2012, 42(12): 1407-1415.(in Chinese)

[8] Lin M C, Shieh L D. Flow visualization and pressure characteristics of a cylinder for water impact[J]. Applied Ocean Research, 1997, 19(2): 101-112.

[9] Cointe R. Hydrodynamic impact analysis of a cylinder[J]. Journal of Offshore Mechanics & Arctic Engineering, 1986, 109(3): 237-243.

[10] Mei Xiaoming, Liu Yuming, Dick K P Yue. On the water impact of general two-dimensional sections[J]. Applied Ocean Research, 1999, 21(1): 1-15.

[11] Tassin A, Jacques N, Alaoui A El Malki, et al. Hydrodynamic loads during water impact of three-dimensional solids: modelling and experiments[J]. Journal of Fluids and Structures, 2012, 28: 211-231.

[12] Sottorf W. Experiments with planing surfaces[R]. Technical Report Archive & Image Library NANC TM 661, 1932.

[13] Mcbride E E, Fisher L J. Experimental investigation of the effect of rear-fuselage shape on ditching behavior[R]. Technical Report Archive & Image Library NANC TN 2929, 1953.

[14] Streckwall H, Lindenau O, Bensch L. Aircraft ditching: a free surface/free motion problem[J]. Archives of Civil and Mechanical Engineering, 2007, 7(3): 177-190.

王丑丑(1989-)，男，硕士研究生。主要研究方向：飞机水上迫降及其漂浮特性。

吴宗成(1967-)，女，博士，副研究员，硕导。主要研究方向：飞行器气动布局设计、计算流体力学、飞行器工程估算、飞机水上迫降及其漂浮特性。

(编辑：马文静)

国内无人机市场风向标尽在“尖兵之翼”

国内无人机市场风向标“尖兵之翼——中国无人机大会暨展览会”自2006年首次举办至今已将近十年，据悉2016年尖兵之翼将组织三大展会。分别是2016法国里昂国际无人系统展、尖兵之翼——第七届中国无人机大会暨展览会、第二届高交会无人系统展分会场——中国(深圳)国际高新技术成果交易展览会。

“尖兵之翼——中国无人机大会暨展览会”已在北京成功举办五届，深圳成功举办一届，是集学术交流、展览展示、商业洽谈于一体的高层次、大规模的综合性专业活动，在中国无人机领域具有较高的影响力。中国航天科工集团公司、总参六十所、中国兵器工业计算机应用研究所、中国电子科技集团二十所、易瓦特、大疆创新、北斗星通等知名单位均积极参与了尖兵之翼展会。2016年5月，“尖兵之翼——第七届中国无人机大会暨展览会”将于北京举办，新一届展会在以往的基础上将进一步提升层次、扩大规模、丰富内容。

2015年11月17～20日，尖兵之翼首次移师深圳，“第十七届高交会无人系统展分会场——中国(深圳)国际无人系统技术成果交易展览会(CIUVS)”于深圳龙岗大运中心成功举办。110家来自航天、航空、兵器、电子等军工集团及全国参展企业参与了展会，展会取得了丰硕的成果。2016年，尖兵之翼将和高交会再次携手，共同主办第二届CIUVS展会。

在以往办展的基础上，尖兵之翼放眼国际，2016年4月，尖兵之翼将组织国内企业前往法国里昂参展欧洲无人遥感机系统博览会，第一届欧洲无人遥感机系统博览会将于2016年4月6日在法国里昂博览中心举行，展会面积超过6000平方米，将吸引来自全球顶尖的无人机专家和企业共襄盛举。

十年积累创无人机名牌会展，2016尖兵之翼展翅腾飞，2016法国里昂国际无人系统展、尖兵之翼——第七届中国无人机大会暨展览会、第二届高交会无人系统展分会场——中国(深圳)国际高新技术成果交易展览会值得期待！国内无人机市场风向标尽在“尖兵之翼”！

邮箱：gbt@gobetter.com.cn网址：http:∥www.auvsc.cn/

Water Entry Numerical Study of a Simplified Aircraft Model in Ditching

Wang Chouchou, Wu Zongcheng

(School of Aeronautic Science and Engineering, Beihang University, Beijing 100191, China)

Abstract:The rear fuselage suction force plays an important role in the change of attitude angle during aircraft ditching. Basing on Fluent software, using dynamic mesh method, user-defined function, six degrees of freedom model and volume of fluid model, on the beginning, the vertical water entry of 2D circular cylinder, 3D elliptic paraboloid and the horizontal planing of 3D flat plate are numerically studied in detail to validate the reliability of numerical simulation method by comparing with the test results; Then, the ditching of NACA TN 2929 simplified aircraft model is also simulated. The results of which show that the rear fuselage suction force makes the pitch attitude angle changed rapidly, the pitch-up moment of suction force makes the attitude angle increased quickly in water-entry early, when the attitude angle reaches the maximum, the pitch-up moment of suction force is very small, the gravity makes the attitude angle decreased quickly, and this method can be properly used to simulate the rear fuselage suction force and pitch attitude in ditching.

Key words:simplified aircraft model; ditching; numerical simulation; dynamic mesh; suction force; attit-ude angle

作者简介：

中图分类号：V271.9；V212

文献标识码：A

DOI：10.16615/j.cnki.1674-8190.2016.01.008

文章编号:1674-8190(2016)01-051-11

通信作者：王丑丑,buaa_wcc@163.com

收稿日期：2015-11-02；修回日期：2015-12-16