考虑工程约束的高可信度气动外形优化设计

雷国东，钟敏，郑遂

(中国航空研究院 飞行物理研究中心，北京　100012)



考虑工程约束的高可信度气动外形优化设计

雷国东，钟敏，郑遂

(中国航空研究院 飞行物理研究中心，北京100012)

摘要：实际气动设计中遇到的工程问题较为复杂，然而能够用于实际工程设计的高可信度气动外形优化设计工具较少。基于飞行器设计工程实际中的各种复杂气动约束和几何约束要求，集成高可信度非结构网格RANS方程求解器、弹簧比拟网格变形技术、FFD外形参数化、RBF代理模型、粒子群优化器，构建多设计点气动外形优化设计工具，并应用于先进低速层流翼型和高亚声速超临界机翼的气动外形优化设计中(包括单设计点和多设计点)，进行考虑/不考虑气动约束和几何约束的气动外形优化设计分析。结果表明：多设计点气动外形优化设计工具有效，约束条件和智能优化器自动有效地引导了层流翼型和亚声速机翼外形的有利改变。

关键词：气动约束；几何约束；FFD外形参数化；RBF代理模型；粒子群优化器

0引言

飞行器设计过程中使用高可信度的计算流体力学(CFD)方法逐渐普遍化，设计人员不仅希望有一个高可信度的流场分析工具(例如各种CFD软件)，更希望具有自动化功能的高可信度设计工具[1]。早期的气动优化设计大多基于低可信度的CFD模型(例如波音公司的TRANAIR软件)，无法覆盖整个飞行包线内的流动。而实际工程的气动优化设计通常是一个多设计点、关注细节(特别是民用飞机)并包括多种复杂的气动和几何限制的有约束优化过程，因此迫切需求基于N-S方程求解器的高可信度优化设计方法和工具，但是与高可信度的气动分析工具相比，目前高可信度的气动优化设计工具不够成熟，在国内的工程设计中应用并不普遍。

高可信度的气动优化技术包括高可信度的气动分析和高可信度的代理模型，例如Huang Likeng[2]利用Co-Kriging代理模型技术构建多层次可信度的气动优化技术。

目前高可信度气动外形优化设计研究主要有三类策略：①耦合高可信度CFD求解器的直接优化设计；②基于伴随方程的优化设计(Adjoint Based Optimization，简称ABO)，该方法由Antony Jameson等提出，典型文献见[3-4]，目前在NASA FUN3D、DLR TAU软件、商业CFD软件Fluent、Star CCM+等上均获得应用，国内陈颂等[5]在自主开发的气动设计软件也集成了该方法；③基于代理模型的优化设计(Surrogate Based Optimization，简称SBO)，典型的技术总结见文献[6]，具体的实现技术是采用了实数编码的遗传算法构建的气动外形优化技术[7-9]。

第①类策略对计算资源的要求极高，经费和时间消耗极大；第②类策略(SBO)型在三类策略中具有计算量居中，时间消耗最少，算法简单且鲁棒性高，可以采用梯度或者全局性寻优方法，易于扩展解决多设计点优化问题；第③类策略(ABO)型在三类策略中计算量最小，但是基于梯度的优化方法只能得到局部优化结果，推进式的优化并行效率不高，不能充分发挥大型计算集群的功能，算法复杂难以扩展解决多设计点优化设计问题。

由于实际气动设计中遇到的工程问题较为复杂，而工程问题需要完整性的解决方案，能用于实际工程设计的高可信度气动外形优化设计工具较少，目前国内设计人员改进飞行器的气动性能主要通过经验试凑和低可信度的方法，在研的一些高可信度气动优化设计工具通常是基于结构网格求解器，设计人员应用不方便。

本文从实际气动设计需求出发，阐述充分考虑多种工程实际气动约束和几何约束的气动外形优化设计技术，集成非结构网格RANS方程求解器、自由变形(Free Form Deformation，简称FFD)外形参数化、RBF代理模型、粒子群优化算法、多设计点优化设计等技术以提升高可信度气动优化设计技术在飞行器设计过程中的成熟度，推动其广泛应用。

1气动求解器

1.1控制方程

采用直角坐标系下的三维可压缩流动N-S方程，守恒型RANS方程可写成[10]：

(1)

(2)

(3)

(4)

(5)

μtot=μ+μtur

(6)

(7)

式中：Ω为求解域；t为时间；ρ为密度；p为静压；T为静温；vi为速度分量；H为焓；δij为克罗内克函数；S为其他源项；μ和μtur为粘性系数与湍流粘性系数；Prd和Prt为普朗特数与湍流普朗特数。

1.2湍流模型

采用Spalar-Allmaras湍流模型(简称SA湍流模型)[11]，通过求解与湍流粘性系数有关的单一场方程得到湍流粘性系数。SA湍流模型方程如下：

(8)

湍流粘性系数

(9)

1.3数值离散方法

采用基于格点的有限体积法离散守恒型控制方程，在非结构网格特别是全四面体网格中，格点的数量约为网格的1/5～1/6，围绕格点构建控制体(如图1所示)能够大幅地减少计算量，以节点为中心、连接接网格中心、网格面中心、网格棱边中点构成的小三角面片组成的多面体作为空间离散的控制体[11]。

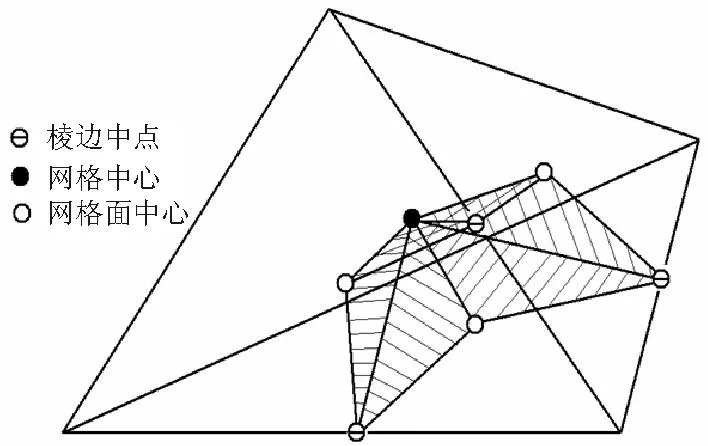
图1　对偶剖分及控制体的构建

积分型式的控制方程为

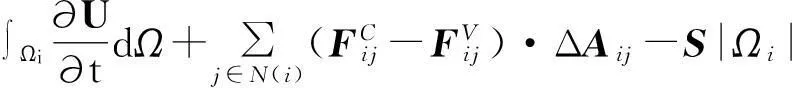
(10)

本文求解器的无粘通量算法有中心格式(JST格式)和迎风格式(ROE格式)，中心格式(JST格式)无粘通量计算方法如下：

(11)

(12)

(13)

(14)

λi=∑k∈N(i)λik

(15)

φij=4φi/(φi+φj)

(16)

φi=[λi/(4λij)]p

(17)

(18)

(19)

(20)

(21)

式中：N(i)为i点邻节点集合；pi为i点压力；S2和S4为延伸参数；Ni为i点邻节点数；κ(2)和κ(4)为延伸参数。

迎风格式(ROE格式)无粘通量计算方法如下：

(22)

粘性通量计算中的梯度项处理方法如下：

(n-αfs)

(23)

αf=s·n

(24)

式中：n为相邻控制体界面单位法向量；s为相邻控制体中心连线单位向量。

本文求解器采用时间推进方法求解稳态流场问题，时间项处理如下：

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

aij=(ai+aj)/2

(33)

(34)

式中：Vij为控制体网格面中心速度分量；NCFL为CFL数；Aij为i节点和j节点构成棱边网格面面积；μij为i节点和j节点构成棱边中点处粘性系数；nij为i节点和j节点构成棱边单位方向矢量；aij为i节点和j节点构成棱边中点处声速；ai为i节点处声速。

1.4网格变形方法

采用网格变形的方法批量自动化地生成样本计算网格，网格变形(包括边界层网格)采用弹簧比拟法，该方法对于全四面体网格稳健性较好，各向异性四面体网格边界层的生成相对三棱柱网格边界层较为容易，四面体是空间填充性最好的基本几何体，对于基于格点的求解器还具有计算量小的特点。基于Hook定律，对于每一个网格节点，受到的合力可写为

Fi=∑j∈N(i)Kij(Δxj-Δxi)

(35)

刚性系数定义为

(36)

根据节点受力平衡

(37)

(38)

(39)

式中：n为迭代次数；N(i)为节点i的邻节点集合；xi为i节点坐标。

1.5外形参数化方法

外形参数化方法是构建优化设计系统或方法的关键技术，工程实际的几何外形都是三维情形，尽管二维问题可扩展为三维问题统一处理，但是使用二维参数化方法可以使问题得到极大的简化，给出二维翼型的参数化处理方法，即Hicks-Henne参数化方法；对于三维几何外形，例如三维机翼，则采用通用性更强的FFD参数化方法。

Hicks-Henne参数化方法是一种扰动参数化方法，采用一系列凸包函数的叠加对原始翼型物面网格进行扰动以达到改变翼型几何外形的目的，参数化的翼型几何外形可描述为

(40)

(41)

(42)

FFD外形参数化方法是一种通用性较好，功能强大的外形参数化方法[12]，用于驱动物面网格变形，体网格变形则采用前面的弹簧比拟方法。用于处理几何约束的几何外形变形也采用FFD外形参数化方法。

x(u,v,w)=

(43)

对于二维翼型，初始坐标数据已知，变形方法也是确定的，因此样本翼型的坐标数据可以推算得到，参数化方法可以用于驱动体网格变形和几何约束的计算。由于两种参数化方法用到的基函数均是光滑函数，在初始几何外形具有良好光滑性的基础上，这两种几何外形参数化方法给出的优化几何外形也具有较好的光滑性；这两种参数化函数导致的几何外形变形是在初始几何外形基础上的光滑扰动，优化后的几何外形能否出现非物理的变形则是由智能优化算法和各种气动约束和几何约束所决定，通过后面的算例予以证明。

2智能优化器

2.1代理模型

对于工程数值仿真优化问题(包括气动外形优化设计)，由于高可信度的数值仿真计算量较大，直接将采用高可信度的数值仿真嵌入智能优化器，代价极大而且效率极低。代理模型是解决这一问题的较好技术，可以降低计算费用，提高优化效率。代理模型中的样本计算并行度极高，适宜应用计算机集群计算。代理模型的种类较多，包括二次多项式、Kriging函数、RBF函数(RadialBasisFunction)、人工神经网络ANN等。本文采用的基于RBF函数的代理模型是其中一种数学模型，简单、适应性广，是健壮性较好的代理模型[6]。

RBF函数插值原理：

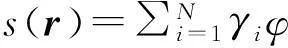
(44)

本文的RBF函数φ(ξ)采用WendlandC2函数：

(45)

ξ=‖r-ri‖/R

(46)

使用代理模型能够大幅减少计算时间的原因是：(1)替代优化器中对高可信度求解器的反复调用，样本目标函数和各种约束的高可信度计算是智能优化系统计算量的绝大部分，而代理模型与之相比是一个微小量，(2)多层次的并行性，各个样本计算之间没有信息交互，完全是独立的，由于每一个样本的高可信度计算本身可调用一定规模的并行计算，样本群的计算也可在更粗一级的粒度上实现并行计算，两个不同粒度的并行性为调用大批量计算资源减少计算时间提供了可能。

2.2粒子群算法

粒子群算法是一种群智能优化算法，粒子群优化算法是对鸟群捕食群体智能的模拟，如果多维空间有一块食物，模拟鸟群群体智能搜索的过程，单个鸟儿不仅依靠自身的认知能力搜索食物，同时也观察其他鸟儿搜索的情况(即社会认知)，以便随时调整自身的认知，从而更快找到食物的准确位置。与遗传算法[13-14]相比，粒子群优化算法没有选择、交叉、变异模块，适合实数建模，简单高效。粒子群算法的数学原理是以速度和位移模型给出的，一种任意单个粒子的运动速度模型如下：

Vid=wVid+c1r1(pid-xid)+c2r2(gd-xid)

(47)

位移更新模型：

xid=xid+Vid

(48)

式中：w为粒子运动速度的惯性权；Vid为粒子i的d维速度分量；pid为粒子i的d维自身最佳位置；xid为粒子i的d维位置分量；gd为粒子群的d维全局最佳位置；c1和c2为常数；r1，r2为0～1的随机数，模拟鸟群速度分布的多变性。

上述速度模型公式中，wVid为惯性速度项，描述每一个粒子上一秒速度对下一秒速度的影响；c1r1(pid-xid)为自身认知项，描述单个粒子对自身认为的最佳捕食位置的速度反应；c2r2(gd-xid)为社会认知项，描述单个粒子对粒子群公认的最佳捕食位置的速度反应。收敛情况下，自身认知和社会认知将趋于同一位置。

(1) 例1

为了形象阐述粒子群优化算法的全局搜索性能，采用函数y=xsinx，x∈[0,4π](如图2所示)测试粒子群算法能否找到全局最小值，而不是局部最小值，此函数有两个极小值。

图2　曲线y=xsinx

均匀分布初始样本即粒子群的初始位置，如图3所示。优化迭代收敛情况如图4所示。

图3　粒子群初始位置分布

图4　优化迭代收敛情况

从图4可以看出：粒子群优化算法很快便收敛到全局最小值，并没有在非全局最小值附近停留。

(2) 例2

简单的二维问题可以显示粒子群算法的优化性能，对于二维函数：

可以看出该函数在x=-1.5，y=3.0时，z=0最小。

二维问题优化迭代收敛示意图如图5所示。

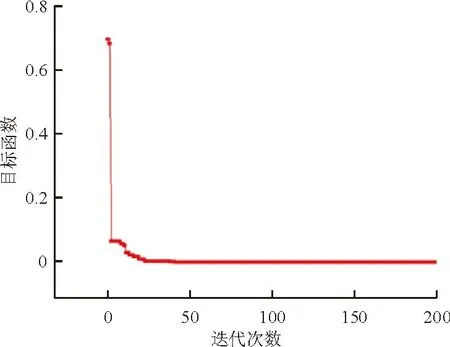
图5　二维问题优化迭代收敛示意图

从图5可以看出：采用均匀分布的初始样本即粒子群的初始位置，粒子群算法很快便找到了该测试函数的最小值。

2.3多目标方法

权系数的选取可以由经验获得(例如本文机翼双设计点优化设计时采用0.5和0.5)，该种处理简单有效。线性加权处理方法的主要问题是构造帕内托前沿时，即使权系数均匀分布，前沿点也很难均匀分布，因此需要采用其他技术处理，但是工程人员只需要一组有效的多目标优化值，线性加权即可做到。

2.4气动约束处理

在SBO型优化思路下，气动约束的处理也可用代理模型的方法处理，将各个样本的气动约束分别计算出来，构建代理模型。采用罚函数法将有约束优化转化为无约束优化。

气动约束：CA0≤CA≤CA1

目标函数：Fobj

转为无约束的目标函数：

max[0,-(CA1-CA)]}

(49)

式中：β为惩罚因子。

2.5几何约束处理

实际飞行器设计工程中几何外形不可能完全按照气动最优的几何设计，几何外形必须在一定的限制下设计，这些限制即几何约束，几何约束非常重要，例如机翼前后梁的高度影响机翼的结构强度和内部油箱的设计。几何约束处理类同于气动约束处理。

几何约束：GA0≤GA≤GA1

目标函数：Fobj

转为无约束的目标函数：

max[0,-(GA1-GA)]}

(50)

式中：β为惩罚因子。

对于三维机翼气动优化设计，各个控制剖面的翼型所有坐标点数据已知，FFD变形后的所有坐标点数据也可计算得到，并且计算量不大，因此各个剖面的最大相对厚度和某些弦向比例位置处的相对厚度等均可计算得到，形成样本数据集，构建代理模型，如图6所示，对于每个翼型剖面，约束前梁、后梁和最大厚度处的相对厚度。

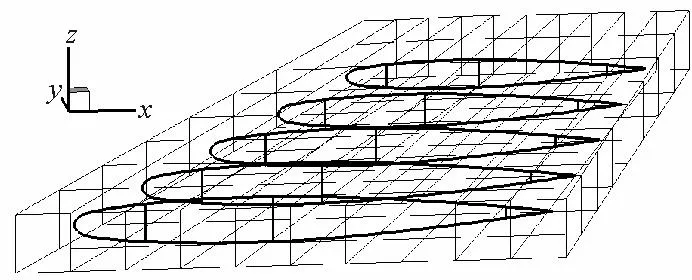
图6　用于几何约束处理的FFD框

2.6优化流程组织

优化流程采用C++语言和Linux-shell编程，批量计算作业任务采用OpenPBS软件，不同部件之间的交互采用数据文件，具体流程如下：

(1) 网格生成

根据初始几何外形，生成初始气动计算网格，生成施加几何约束的初始控制翼剖面，以散点数据形式给出。

(2) 文件配置

气动计算文件配置，Hicks-Henne控制点或FFD框控制点设置，采用拉丁-超立方方法生成设计变量样本集文件。

(3) 网格变形

根据设计变量样本集，参数化算法驱动初始表面网格变形，辅以弹簧比拟法驱动体网格变形，自动批量生成样本网格；参数化算法驱动初始控制翼剖面散点移动，生成样本控制翼剖面散点集。

(4) 批量计算

调用高可信度CFD程序计算各个样本气动力系数和样本控制翼剖面的几何约束。

(5) 数据收集

收集样本气动力系数和几何约束，形成气动力系数样本集和几何约束样本集。

(6) 代理模型

根据气动力系数样本集和几何约束样本集，构建气动力系数代理模型和几何约束代理模型。

(7) 智能优化

调用智能优化器进行单设计点或多设计点优化，得到优化设计变量。

(8) 几何重构

根据优化设计变量，采用网格变形程序得到优化网格并计算气动力系数，采用参数化方法得到优化后的控制翼剖面散点数据并计算几何约束。得到的优化气动力数据和几何约束用于检验优化流程的有效性，如果优化有效，根据优化后的表面网格重构优化后的几何外形。

3验证算例

3.1低速层流翼型优化设计

以GAW-1翼型为原始翼型，以Hicks-Henne参数化方法构建批量样本几何外形，考虑三个设计点(巡航、爬升和最小平飞状态)，并考虑翼型表面为部分层流状态。

巡航状态(如表1所示)：高度为3 000m，Ma=0.313，升力系数定为0.4。

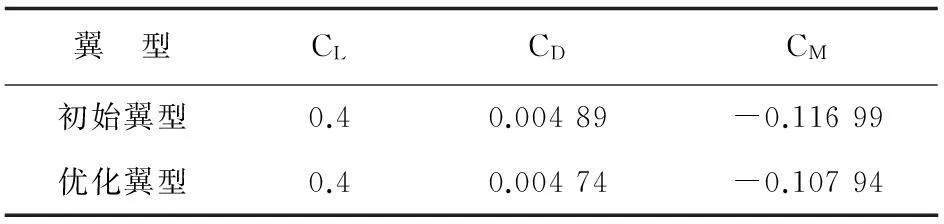
表1　巡航状态

爬升状态(如表2所示)：高度为海平面状态，Ma=0.189，升力系数定为0.88。

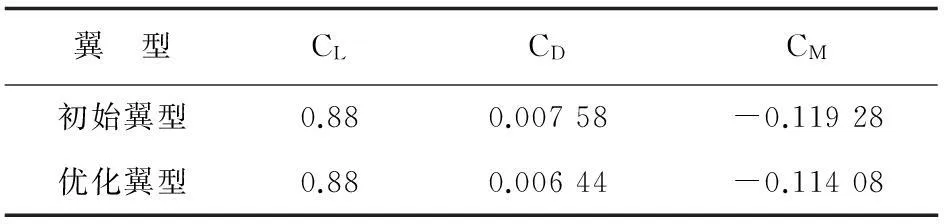
表2　爬升状态

最小平飞状态(如表3所示)：Ma=0.091，高度定为海平面状态。

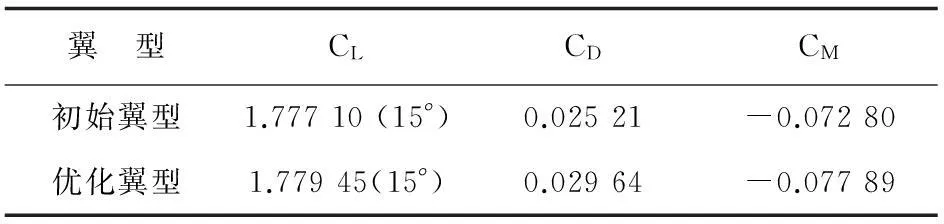
表3　最小平飞状态

从表1～表3可以看出：三个设计点在满足所设定的气动约束和几何约束的前提下，前两个设计点阻力系数小于GAW-1翼型，而第三个设计点设计攻角的升力系数大于GAW-1翼型。

前两个设计点的气动约束除了升力系数约束，还包括低头力矩系数不高于初始翼型，这两个设计点的设计目标为阻力系数；第三个设计点的目标为升力系数，要求α=15°时升力系数高于初始翼型，但是对阻力系数和俯仰力矩系数没有约束；三个设计点的几何约束为翼型最大相对厚度17%不变。以GAW-1翼型为原始翼型，优化前后的翼型形状如图7所示。

图7　优化前后对比(GAW-1翼型)

3.2高亚声速超临界机翼优化设计

以高亚声速超临界机翼CAE-AVM为初始机翼[15](如图8所示)，虽然此机翼巡航设计点Ma=0.85，但本文研究其在Ma为0.77和0.79时的气动性能。以FFD参数化方法构建批量化样本几何外形(如图9所示)，考虑两个设计点，第一个设计点Ma=0.77，α=1°，海拔高度为13 000m；第二个设计点Ma=0.79，α=1.92°，海拔高度为13 000m。两个设计点的优化目标函数均为阻力系数，气动约束为保证升力系数和俯仰力矩系数不变，几何约束为保持前梁、后梁和最大相对厚度处的相对厚度不变，前梁位置为20%当地弦长，后梁位置为70%当地弦长，最大相对厚度位置可以浮动。几何约束是施加在展向y=(1.275 23m，7.281 55m)区间均匀分布的7个翼剖面上。采用SA湍流模型计算粘性效应，采用各向异性四面体划分边界层。FFD框采用的xyz方向框条数目为(11，9，2)，设计变量为FFD框节点z坐标移动量，移动范围定为(-0.03m，0.03m)，采用拉丁超立方方法构造500个样本。

(a) 高亚声速超临界机翼外形

(b) 翼根部位各向异性四面体边界层表面网格

图9　高亚声速超临界机翼的FFD框

3.2.1单设计点优化

分别单独考虑第一和第二设计点，且仅考虑气动约束，气动约束是保持两个设计点各自的升力系数和俯仰力矩系数不变，从CFD程序验算后的优化结果如表4～表5所示。

表4　单独考虑第一设计点优化前后气动力/力矩系数

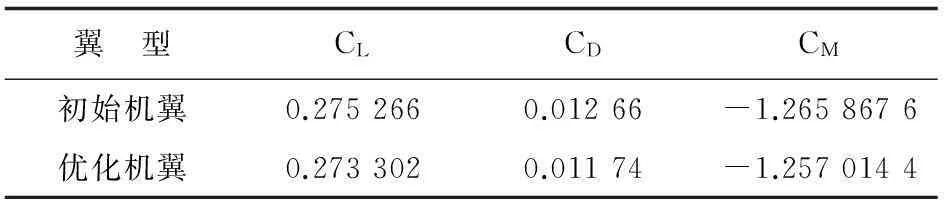
表5　单独考虑第二设计点优化前后气动力/力矩系数

从表4～表5可以看出：第一设计点阻力系数减小了6.8个单位，升力系数和俯仰力矩系数近似满足约束；第二设计点阻力系数减小了9.2个单位，升力系数和俯仰力矩系数近似满足约束，优化程序和代理模型较好地起到了引导气动外形优化的作用。

3.2.2双设计点优化

(1) 不考虑几何约束

采用上下两个设计点的样本数据，但是要求一套设计变量对两个设计点同时优化，目标函数仍是阻力系数，气动约束是保持两个设计点各自的升力系数和俯仰力矩系数不变，且不考虑几何约束，优化前后气动力系数如表6～表7所示。

表6　第一设计点气动力系数(共两个设计点)

表7　第二设计点气动力系数(共两个设计点)

从表6～表7可以看出：两个设计点的阻力系数分别降低了6.0个阻力单位和7.4个阻力单位，而升力系数和俯仰力矩系数基本保持不变。

60%展向位置的翼剖面变化如图10所示。

图10　优化前后机翼展向60%站位处翼型变化示意

(2) 考虑几何约束

同时考虑气动约束和几何约束的双设计点优化，气动约束是保持两个设计点各自的升力系数和俯仰力矩系数不变；几何约束是考虑前梁、后梁和最大相对厚度处相对厚度不变，共21个几何约束，样本几何约束通过FFD变形初始翼剖面坐标获得。采用前面两个设计点的气动力系数样本数据，两个设计点的优化结果如表8～表9所示。

表8　第一设计点气动力系数(共两个设计点　几何约束)

表9　第二设计点气动力系数(共两个设计点　几何约束)

从表8～表9可以看出：两个设计点的阻力系数分别降低了2.6个阻力单位和3.3个阻力单位，而升力系数和俯仰力矩系数基本保持不变。

60%展向位置的翼剖面变化如图11所示。

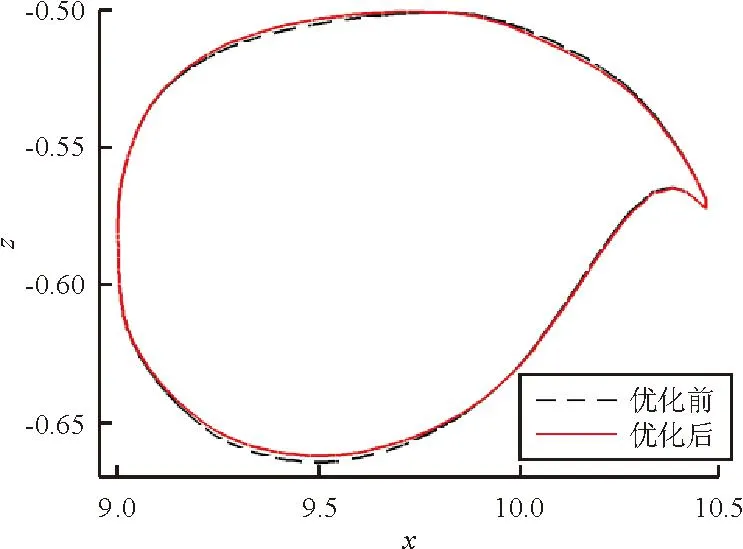
图11　优化前后机翼展向60%站位处翼型变化

(3) 不考虑/考虑几何约束对比

如果不施加几何约束，前梁和最大厚度位置处相对厚度减小，从而不利于机翼结构和油箱的设计。由于约束了前后梁处和最大相对厚度处的相对厚度，机翼前后梁和最大厚度处将只能同时上移、同时下移或者不变，从而维持三个位置的相对厚度不变，从给出的翼剖面形状可以看出，智能优化器自动化地引导了几何外形改变。几何约束施加处的相对厚度增量(优化后-优化前)分布曲线如图12所示。

图12　几何约束处优化前后相对厚度变化量

从图12可以看出：仅有最大不超过0.1%的的相对厚度增加(相对厚度增加有利于前后梁和油箱的设计)，优化器在使气动约束和几何约束满足的同时有效地减小了两个设计点的阻力系数。

4结束语

(1) 本文通过集成计算流体力学、参数化几何、多目标优化三个方面的技术构建了一套适合实际工程设计要求的飞行器气动外形优化设计工具，并应用该工具进行了低速层流翼型和高亚声速超临界机翼多设计点外形优化设计。

(2) 无论是低速翼型还是高亚声速机翼，在满足各种气动约束和几何约束的前提下，优化后的几何外形均具有与初始几何外形相当的光滑性，并且各个设计点气动性能的改善较为显著，从而验证了本文优化设计工具和方法的有效性。

(3) 本文后续将开展翼身组合体及全机构型的气动外形优化设计、多种代理模型技术、多重FFD框及网格大变形技术研究，以增强本文设计工具的工程实用性。

参考文献

[1]SergeyPeigin， 朱自强，BorisEpstein. 可用于民机空气动力设计中的数值优化方法[J]. 航空学报， 2014, 35(1): 58-68.

SergeyPeigin,ZhuZiqiang,BorisEpstein.Applicablenumericaloptimizationmethodsforaerodynamicdesignofcivilaircraft[J].ActaAeronauticaetAstronauticaSinica, 2014, 35(1): 58-68.(inChinese)

[2]HuangLikeng,GaoZhenghong,ZhangDehu.Researchonmulti-fidelityaerodynamicoptimizationmethods[J].ChineseJouralofAstronautics, 2013, 26(2): 279-286.

[3]AntonyJameson，ThomasVJones.Airplanedesignwithaerodynamicshapeoptimization[EB/OL].(2011-02-01)[2016-01-21].http:∥aero-comlab.stanford.edu/papers/stanford_optimization_20110201.pdf

[4]ReutherJ,JamesonA.Aerodynamicshapeoptimizationofwingandwing-bodyconfigurationsusingcontroltheory[R].AIAA-95-0123, 1995.

[5] 陈颂， 白俊强， 史亚云， 等. 民用客机机翼/机身/平尾构型气动外形优化设计方法研究[J]. 航空学报， 2015, 36(10): 3195-3207.

ChenSong,BaiJunqiang,ShiYayun,etal.Aerodynamicoptimizationdesignofciviljetwing-body-tailconfiguration[J].ActaAeronauticaetAstronauticaSinica, 2015, 36(10): 3195-3207.(inChinese)

[6]SlawomirKoziel,DavidEcheverríaCiaurri,LeifurLeifsson.Computeroptimization,methodsandalgorithm[M].Germany:Springer, 2011: 33-59.

[7]NorbertKroll.Numericalmethodsformultidisciplinaryanalysisandoptimization[C]∥NorbertKroll.CAE-DLRAerodynamicSeminar2011.Beijing:CAE-DLR, 2011: 78-96.

[8]NorbertKroll,BrezillonJ,Abu-ZuraykM,etal.Progressinnumericalshapeoptimization[C]∥NorbertKroll.DLR-CAEAerodynamicsSeminar2013,Beijing,P.R.China:CAE-DLR, 2013: 1-74.

[9]TerryLHolst,ThomasHPulliam.Aerodynamicshapeoptimizationusingareal-number-encodeedgeneticalgorithm[EB/OL].(2001-07-11)[2016-01-21].http:∥people.nas.nasa.gov/～pulliam/mypapers/AIAA-2001-2473.pdf

[10] 任玉新， 陈海昕. 计算流体力学基础[M]. 北京： 清华大学出版社， 2006： 7-13.

RenYuxin,ChenHaixin.Thebasiccomputationalfluiddynamics[M].Beijing:TsinghuaUniversityPress， 2006: 7-13.(inChinese)

[11]BlazekJ.Computationalfluiddynamics:principlesandapplications[M]. 2nded.Germany：Elsevier, 2005: 240-247.

[12]JamshidA.Samareh.Asurveyofshapeparameterizationtechniques[C]∥NasaLangleyCenter.Ceas/AIAA/Icase/NasaLangleyInternationalForumonAeroelasticityandStructuraldynamics.USA：NASA， 1999: 333-343.

[13]MarianNemec,DavidWZingg.Multi-pointandmulti-objectiveaerodynamicshapeoptimization[EB/OL].(2002-09-04)[2016-01-21].http:∥people.nas.nasa.gov/～pulliam/mypapers/aiaa-2002-5548.pdf.

[14] 潘峰， 李位星， 高琪. 粒子群优化算法与多目标优化[M]. 北京： 北京理工大学出版社， 2013： 137-146.

PanFeng,LiWeixing,GaoQi.Particleswarmoptimizerandmulti-objectoptimization[M].Beijing:BeijingInstituteofTechnologyPress, 2013: 137-146.(inChinese)

[15]JunHua,SuiZheng,MinZhong,etal.Designandverificationstudyofanaerodynamicvalidationmodel[R].APISAT-2015,Australia:RAeSAustralianDivision, 2015.

雷国东(1980-)，男，博士，高级工程师。主要研究方向：计算流体力学、飞行器气动设计。

钟敏(1987-)，女，硕士，工程师。主要研究方向：计算流体力学、飞行器气动设计。

郑遂(1959-)，男，博士，研究员。主要研究方向：飞机总体与气动设计。

(编辑：赵毓梅)

High-fidelity Aerodynamic Shape Optimization and Design with Engineering Constraints

Lei Guodong, Zhong Min, Zheng Sui

(Flight Physics Research Center, Chinese Aeronautical Establishment, Beijing 100012, China)

Abstract:Engineering problems is complex in actual aerodynamic design, but high-fidelity aerodynamic shape optimization and design tool is scarcity. Aimed at the complicated aerodynamic constraints and geometry constraints of the aircraft design engineering， the high-fidelity unstructured-grid RANS equation solver, the spring dynamic mesh method, the FFD geometry parameterization method, the RBF function surrogate model and the PSO optimizer are integratedto build an aerodynamic shape multi-point optimization and design tool. It is employed for the advanced low-speed laminar-flow airfoil shape design and the high subsonic supercritical wing shape design via the single-point and multi-point cases, with/without the aerodynamic and the geometry constraints. The results show that the tool works, and the constraints and the intelligence optimizer automatically and effectively guide the airfoil and wing shape to change with improved aerodynamic performances.

Key words:aerodynamic constraints; geometry constraints; FFD geometry parameterization; RBF function surrogate model; PSO optimizer

作者简介：

中图分类号：V211

文献标识码：A

DOI：10.16615/j.cnki.1674-8190.2016.01.018

文章编号:1674-8190(2016)01-124-11

通信作者：雷国东,leigd@cae.ac.cn

收稿日期：2015-12-14；修回日期：2016-01-21