基于粗糙集理论的翼型参数优选方法研究

刘卓，李自启，梁滨，杨波，魏斌斌，高永卫

(1.江西洪都航空工业集团有限责任公司 650所，南昌　330024)

(2.西北工业大学 航空学院，西安　710072)



基于粗糙集理论的翼型参数优选方法研究

刘卓1，李自启1，梁滨1，杨波2，魏斌斌2，高永卫2

(1.江西洪都航空工业集团有限责任公司 650所，南昌330024)

(2.西北工业大学 航空学院，西安710072)

摘要：在设计机翼时，通常需要进行多目标决策，而教练机机翼翼型选取的先验经验不足，需要进一步研究，从而得出翼型的选择规则。分析国内外已有教练机机翼翼型使用情况，运用粗糙集理论中基于重要度和条件信息熵结合的权重确定方法，提出在机翼方案设计阶段翼型的选择方法；对比分析三种分段方法在翼型性能指标离散化时的优缺点及其原因，并结合算例进行适用性验证。结果表明：在有限数据条件下，两断点方法是比较合适的属性离散化方法。所提出的方法具有使用价值，对飞机设计方案阶段翼型的选择以及机翼的气动设计具有参考意义。

关键词：翼型；教练机；粗糙集

0引言

粗糙集(Rough Set)理论是波兰数学家Z.Pawlak[1-2]在20世纪80年代初首先提出的一种可以分析模糊和不确定问题的数学理论，它的基本思想是通过案例库分类归纳出概念和规则。经过近三十年的发展，该理论已在机器学习、决策分析、模式识别、人工智能和数据挖掘等领域实现了成功的应用。粗糙集理论最大的优点是在进行数据处理的过程中不需要先验知识，不受外界主观因素的影响，仅利用现有数据样本进行分析处理，具有高度的客观性，特别适用于进行产品改型设计却又缺乏系统理论支持的情况。粗糙集的上述特点相比模糊理论等其他需要依赖专家系统的决策方法具有较大优势。

多目标决策中，在进行各目标或属性(备选方案的特征、品质或性能参数)的评判和决策过程中通常会使用权重的概念，用权重反映各个因素在评判和决策过程中所占有的地位和所起的作用。因而，能否准确地确定权重直接影响到最终的评判和决策结果。

常用的权重确定方法有专家评分法、二元对比排序法和模糊统计法等，同时，一些新的研究方法也被运用于确定权重，例如模糊判断矩阵法、组合赋权法、误差分析方法、灰色关联度法和熵权法等。上述方法中，无论是依据决策者主观判断和经验的主观赋权方法，还是基于数学理论和方法的客观赋权方法，都需要依赖先验知识。因此，粗糙集理论不需要先验知识的优点可以弥补传统权重确定方法的不足，使权重确定更具客观性。

目前，已有不少基于粗糙集理论来求取属性权重的研究方法，其中，基于正域重要度的权重确定方法和基于条件信息熵的权重确定方法应用得较为广泛[3-5]。然而，基于正域重要度的权重确定方法，由于其是冗余属性，且决策表分辨能力不足，导致个别属性权重为0；基于条件信息熵的权重确定方法，对冗余属性的赋权过重，导致最终的权重值中冗余属性大于非冗余属性，偏离实质。因此，结合上述两种权重确定方法提出了将重要度和条件信息熵相结合的权重确定方法，提高了粗糙集方法的适用性[6-9]。

机翼的空气动力特性影响飞机的性能，翼型的选取和设计是机翼设计的基础。翼型的外形参数主要包括：最大厚度和厚度分布、最大弯度和弯度分布、前后缘几何参数等。性能参数主要包括：最大升力系数CLmax、失速迎角αs、最小阻力系数CDmin、最大升阻比(L/D)max、升力线斜率CLα和零升力矩系数CM0等。在设计飞机的机翼时，需要综合考虑翼型的外形和性能参数，即需要进行多目标决策。

教练机与一般飞机的典型区别包括：①教练机的主要工况是机动飞行，而非巡航，然而由于缺乏先验经验，教练机方案设计阶段仍只能提出巡航设计要求；②飞机要有足够的安全边界，适合驾驶经验不足的操作者；③教练机要容易进入尾旋，同时也要容易改出等。

在公开的资料中，适合上述要求的机翼/翼型性能并无足够的信息，即关于教练机机翼翼型选取的先验经验不足，需要进一步研究以得出选择规则。

本文运用粗糙集理论中基于重要度和条件信息熵结合的权重确定方法，提出教练机机翼设计过程中，在机翼方案设计阶段翼型的选择方法，对比研究不同分段方法在翼型性能指标离散化时的优缺点及其原因，并采用风洞实验与CFD方法进行算例验证，以证明本文所用方法的适用性。

1教练机翼型参数的确定

1.1基于重要度和条件信息熵相结合的权重

想要利用粗糙集方法，首先需建立决策信息表S=(U,A,V,f)。

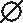
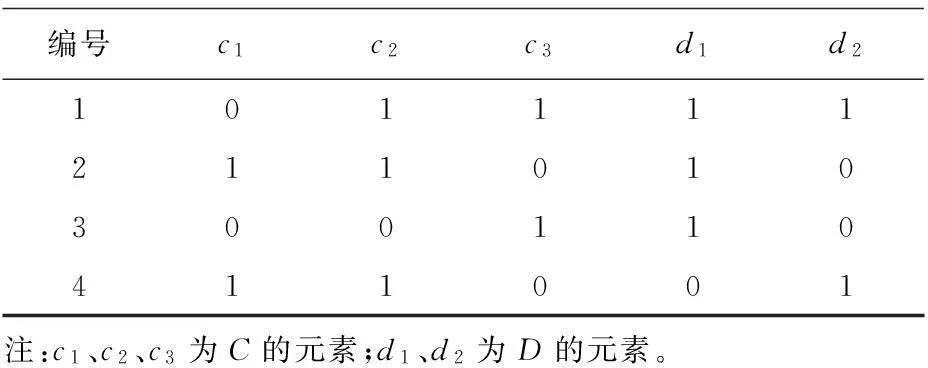
表1　决策信息表示例

基于重要度和条件信息熵相结合的权重计算公式为[8]

(1)

式中：sig(c)为基于信息表示的条件属性c的重要度；μ(c)为基于代数理论的条件属性c的优先级。

将sig(c)和μ(c)结合起来定义权重，一方面考虑到各属性权重不应为0，另一方面考虑原为“非冗余”属性指标的权重应高于原为“冗余”属性指标的权重，使得权重赋值更加合理。

运用基于重要度和条件信息熵结合的权重确定方法，得到在相应决策变量下各个条件属性的权重值，结果为一个权重向量：

W=(w1,w2,…,wm)

(2)

1.2效用函数及其规则化

初始决策信息表中所列条件属性和决策属性的值一般为具有一定意义的连续性数值，若要对其进行粗糙集处理，需要将其赋予数学上的意义。第一步是对各个属性规则化处理，即应用因素效用函数方法将每列属性值化为介于[0,1]的无量纲量，然后便可以使用统一的测度及加权来进行定量评价与比较。

若待评价的属性为m个，且每个属性对应的样本值有n个，则信息表可理解为一个m×n的属性矩阵：

C=(cij)m×n

(3)

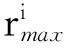
(4)

(5)

则有以下三种数值规则化的情况：

(1) 若属性cij要求越大越好，则采用的效用函数为

(6)

(2) 若属性cij要求越小越好，则采用的效用函数为

(7)

(3) 若属性cij要求应保持在[r1,r2]范围内时，则采用的效用函数为

(i=1,2,…,m)

(8)

第三种情况存在特例，即当属性cij要求尽量接近某一定值r时，可将式(8)作特例处理，得到效用函数：

(i=1,2,…,m)

(9)

从属性数值规则化的过程可以看出：决策对于各个属性的偏好信息已经体现在效用函数的规则化过程中，例如某些属性需要越大越好，某些属性需要趋近一个定值等。将偏好信息用于数值规则化进而完成粗糙集的权重分析，便可达到决策所要求的效用，即因素效用函数的内涵所在。完成各属性的规则化后，数据仍然是连续性的数值，需要进一步做离散化处理。

在分析得到关于方案各个条件属性(参数)的权重后，将方案各条件属性(参数)按照效用函数规则化，得到效用值矩阵

(10)

各个备选方案的相对量化权重值的计算公式为

(11)

比较各个方案的最终综合效用值，该值越大者即表明其所对应的方案越好。

1.3属性的离散化

要进行数字化处理，则必须对连续变量进行相应的离散化处理。

等距离散化方法是将每个属性无量纲化后的值区间用一个或多个断点等距分成多段，并将各段定义为不同等级，再用数字编码组合表示，每个属性的无量纲化值落在某分段内则编码为分段对应的数字。

在有限样本数量的情况下，本文重点研究一断点、两断点和三断点等距离散化方法的优缺点，并提出一种适用于翼型选型的最佳方法。

一断点、两断点和三断点等距离散化方法对应的离散等级分别为两个等级(好、差)、三个等级(好、一般和差)和四个等级(好、较好、一般和差)，分别用数字编码组合表示为(2、1)、(3、2、1)以及(4、3、2、1)。为了得到教练机机翼翼型性能的选择规则，搜集了20架相关教练机机翼翼根和翼梢的翼型作为初始数据样本，忽略先验经验，基于粗糙集理论进行归纳分析。根据设计状态为巡航状态的要求，确定翼型优选的决策变量为翼载和巡航马赫数。列出20种教练机型号相应的决策变量值，统计结果如表2所示。

将关于翼型的条件属性(参数)与决策变量结合可得决策信息表，分别建立关于翼根翼型和翼梢翼型的决策信息表，两者决策变量和对应数值一致。

运用效用函数进行条件属性无量纲化处理，翼型各项性能参数的效用分别为：最大升力系数(CLmax)、失速迎角(αs)及最大升阻比((L/D)max)要求越大越好，最小阻力系数(CDmin)、升力线斜率(CLα)及零升力矩的绝对值要求越小越好。两个决策变量中，翼载和巡航马赫数均要求接近定值，分别为165.65kgf/m2和0.36(针对PC-7飞机)。

首先，按照上述要求进行决策信息表各属性(参数)基于效用函数的无量纲化处理，然后，根据三种离散化方法分别建立离散决策信息表，其中两个决策变量按照各0.5的权重线性加权为一个综合评价指标。所列翼型性能参阅文献[10]。

三种不同离散化方法下翼根翼型的离散决策信息表分别如表3～表5所示，限于篇幅，本文仅列出翼根翼型的相关数据。

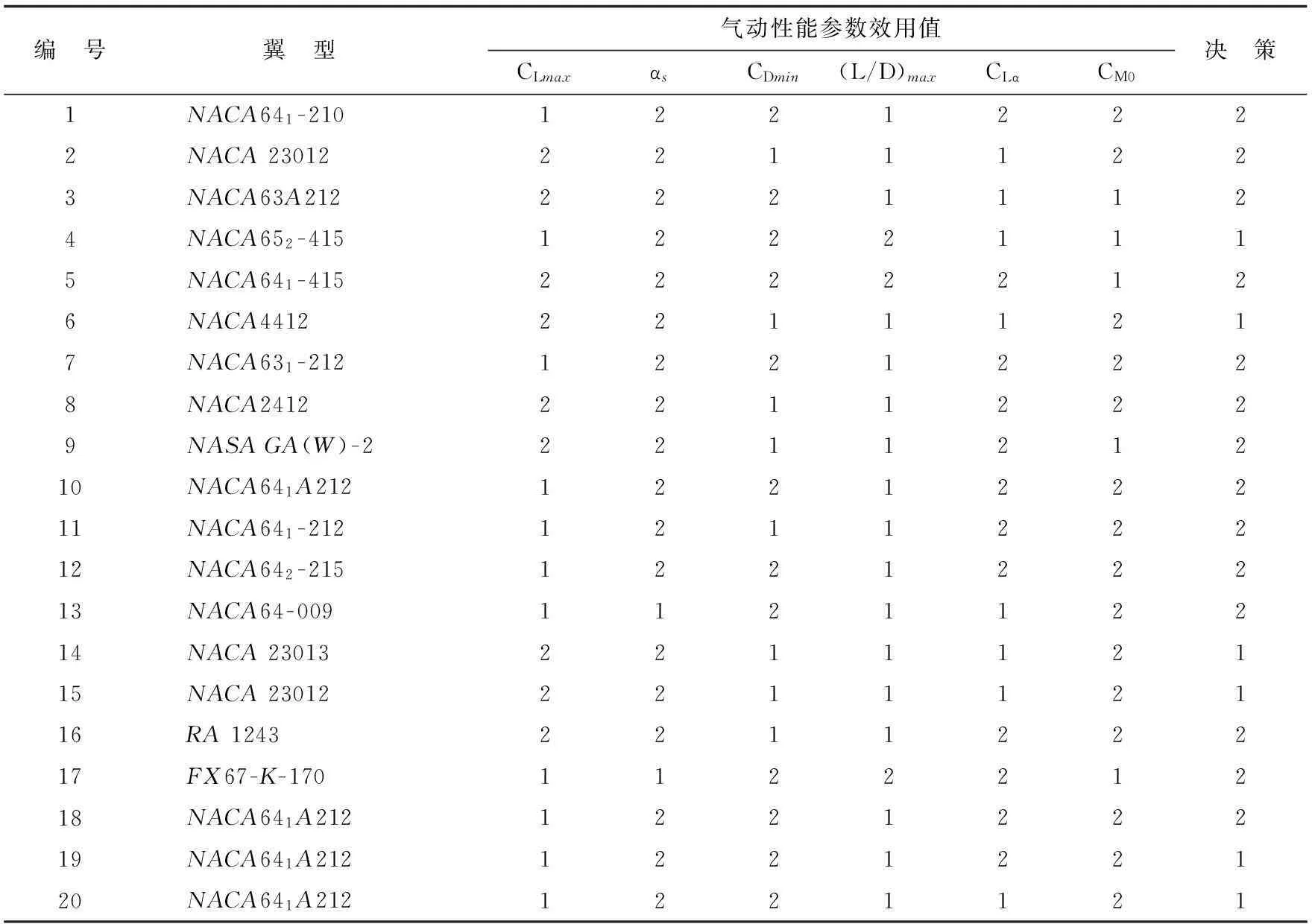
表5　教练机机翼翼根翼型一断点离散决策信息表

利用基于重要度和条件信息熵相结合的条件属性权重确定方法，结合决策信息表(表3～表5)，分别得到三种离散化方法下翼根翼型和翼梢翼型在决策变量约束下各条件属性(气动参数)的权重，如表6～表7所示。

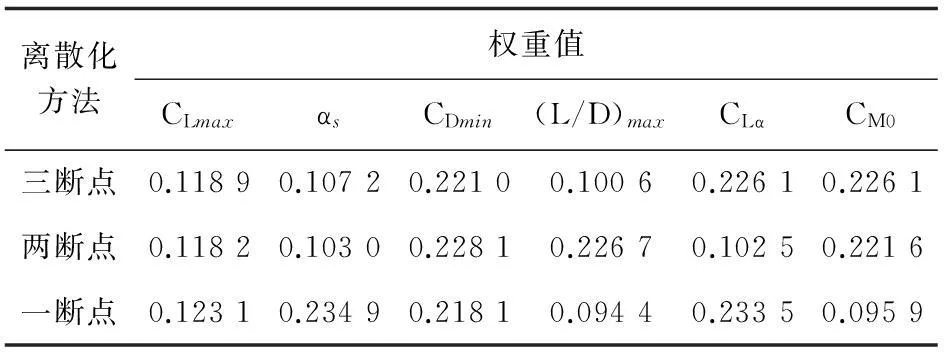
表6　教练机机翼翼根翼型各气动参数的权重值

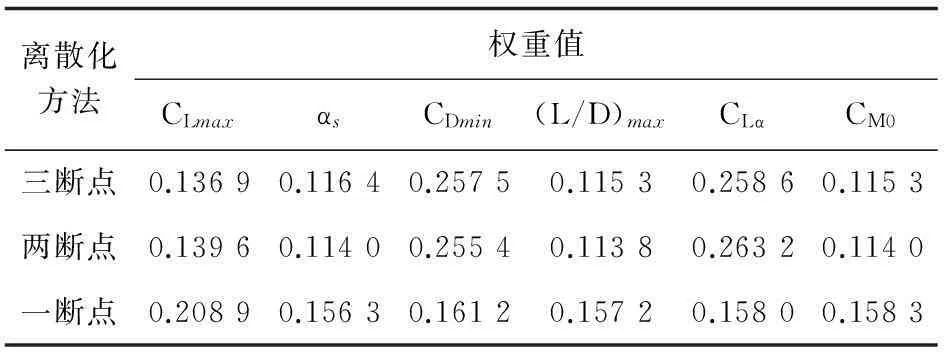
表7　教练机机翼翼梢翼型各气动参数的权重值

从表6～表7可以看出：三种不同离散化方法求得的条件属性(气动参数)的权重存在差别，三断点与两断点离散化方法的结果比较接近，一断点离散化方法的结果偏差较大，这是因为各条件属性的值域范围较大，仅采用一个断点划分容易导致数据失真，离散化后的数据表不能真实反映各翼型对应条件属性的取值状态；两断点与三断点离散化方法结果大致相同，在翼根翼型的分析中两者最大升阻比和升力线斜率对应的权重不同，其中决策变量对应的状态是巡航状态，最大升阻比所占权重应当较大，而三断点离散化方法的结果显示最大升阻比的权重较小，两断点离散化方法的结果更接近合理结果。因此，本文采用两断点等距离散化方法作为连续属性离散化的方法。

由两断点等距离散化方法得到的翼根翼型和翼梢翼型性能参数的权重可知：在决策变量的约束下，翼根翼型最小阻力系数、最大升阻比和零升力矩系数占比重比较大，故翼根翼型的选择更看重上述三个参数；翼梢翼型最小阻力系数和升力线斜率占比重比较大，故翼梢翼型选择时更看重该两个参数。

2算例验证

为了进一步验证教练机机翼翼型优选方法的可行性，根据PC-7飞机性能和上述翼型性能参数选择规则，参照文献[11-12]中的方法，设计两组翼根、翼梢翼型并进行机翼设计对比。限于篇幅，仅列出翼根翼型的设计结果，其气动性能参数如表8所示。

将表8按照效用函数方法做无量纲化处理，得到无量纲化后的效用值数据表，并计算各个备选翼型方案的相对量化权重值，如表9所示。

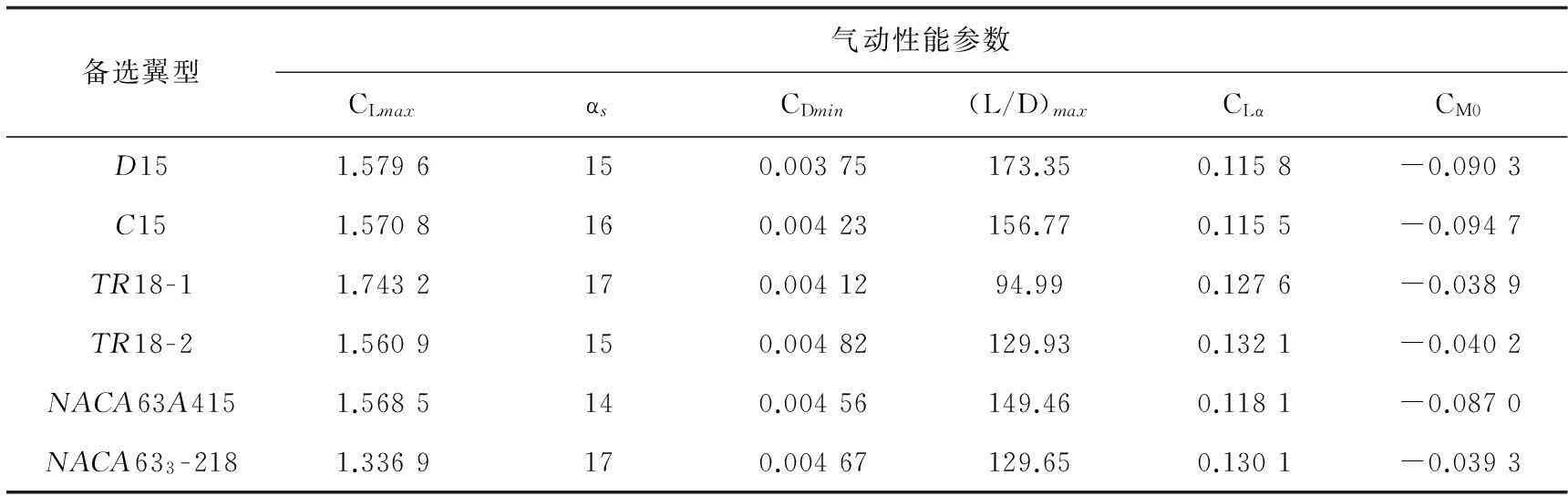
表8　翼根备选翼型的气动参数表

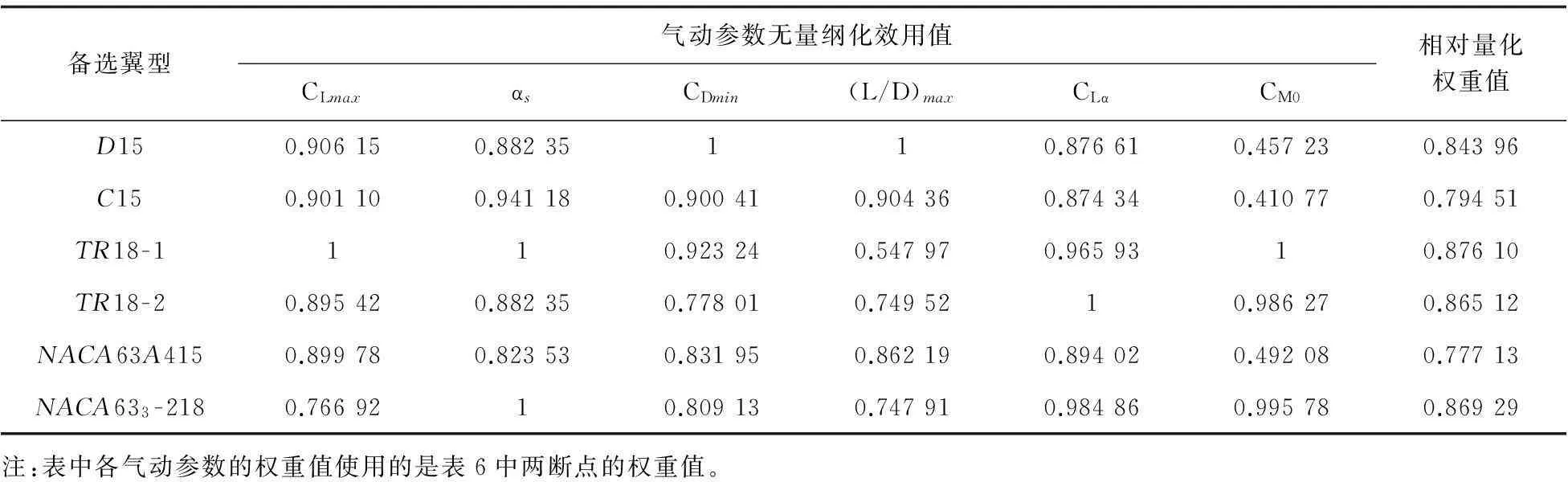
表9　翼根备选翼型的气动参数无量纲化效用值及相对量化权重

从最终的计算结果可知：备选翼型中，翼根翼型以TR18-1的相对量化权重值高，翼梢翼型以TR12-1的相对量化权重值高。表明这一对翼型在翼根翼型和翼梢翼型决策中具有更多趋向于决策的优势。因此，新设计的机翼采用的翼根翼型为TR18-1，翼梢翼型为TR12-1。

经CFD和风洞实验验证，新机翼比基准机翼升阻比高2、最小阻力小约5%，表明根据上述准则选择的翼型取得了满意的效果。

3结论

(1) 运用粗糙集理论，基于重要度和条件信息熵结合的权重确定方法对翼型进行优选的方法是可行的。

(2) 在教练机翼型的权重确定过程中，采用两断点法是合适的。

(3) 在本文的研究范围内，翼根翼型看重最小阻力系数、最大升阻比和零升力矩系数，而翼梢翼型主要参考最小阻力系数和升力线斜率。

参考文献

[1]PawlakZ.Roughsets[J].InternationalJournalofComputerandInformationSciences, 1982, 11(5): 341-356.

[2]PawlakZ.Roughsettheoryanditsapplicationstodataanalysis[J].CyberneticsandSystems, 1998, 29(7): 661-688.

[3] 谭宗凤. 基于粗糙集的权重确定方法研究[D]. 桂林: 广西师范大学, 2012.

TanZongfeng.Researchonmethodofattributeweightbasedonroughsetstheory[D].Guilin:GuangxiNormalUniversity, 2012.(inChinese)

[4] 鲍新中, 张建斌, 刘澄. 基于粗糙集条件信息熵的权重确定方法[J]. 中国管理科学, 2009, 17(3): 131-135.

BaoXinzhong,ZhangJianbin,LiuCheng.Anewmethodofascertainingattributeweightbasedonroughsetsconditionalinformationentropy[J].ChineseJournalofManagementScience, 2009, 17(3): 131-135.(inChinese)

[5] 徐泽水. 几类多属性决策方法研究[D]. 南京: 东南大学, 2002.

XuZeshui.Studyonmethodsformultipleattributedecisionmakingundersomesituations[D].Nanjing:SoutheastUniversity, 2002.(inChinese)

[6] 曹秀英, 梁静国. 基于粗集理论的属性权重确定方法[J]. 中国管理科学, 2002, 10(5): 98-100.

CaoXiuying,LiangJingguo.Themethodofascertainingattributeweightbasedonroughsetstheory[J].ChineseJournalofManagementScience, 2002, 10(5): 98-100.(inChinese)

[7] 陈凤娟, 闫德勤. 知识粗糙性和条件信息熵的关系[J]. 计算机工程与应用, 2009, 45(21): 160-162.

ChenFengjuan,YanDeqin.Relationshipbetweenroughnessofknowledgeandconditionalinformationentropy[J].ComputerEngineeringandApplications, 2009, 45(21): 160-162.(inChinese)

[8] 朱红灿, 陈能华. 粗糙集条件信息熵权重确定方法的改进[J]. 统计与决策, 2011(8): 154-156.

ZhuHongcan,ChenNenghua.Theimprovementofroughsetconditionalentropyweightdeterminingmethod[J].Statisticsanddecision, 2011(8): 154-156.(inChinese)

[9]ZiarkoW.Introductiontothespecialissueonroughsetsandknowledgediscovery[J].InternationalofComputationalIntelligence, 1995, 11(2): 223-226.

[10] 飞机设计手册总编委会. 飞机设计手册： 第6册——气动设计[M]. 北京: 航空工业出版社， 2002.

GeneralEditorialBoardofAircraft Design Manual.Aircraftdesignmanual:Vol6-Aerodynamicdesign[M].Beijing:AviationIndustryPress, 2002.(inChinese)

[11]AbbottIH,AlbertE,VonDoenhoff.Theoryofwingsec-

tions:including a summary of airfoil data[M]. New York: Dover Publications,1959.

[12] Patankar S V, Spalding D B. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows[J]. International Journal of Heat and Mass Transfer, 1972, 15： 1787-1806.

刘卓(1981-)，男，高级工程师。主要研究方向:飞机总体设计。

李自启(1985-)，男，硕士，工程师。主要研究方向:飞机总体设计。

梁斌(1982-)，男，工程师。主要研究方向:飞机总体设计。

杨波(1989-)，男，硕士研究生。主要研究方向:空气动力学。

魏斌斌(1990-)，男，硕士研究生。主要研究方向:空气动力学。

高永卫(1968-)，男，博士，教授。主要研究方向:空气动力学。

(编辑：马文静)

Method of Airfoil Selection in Wing Design Using Rough Set Theory

Liu Zhuo1, Li Ziqi1, Liang Bin1, Yang Bo2, Wei Binbin2, Gao Yongwei2

(1.650 Research Institute, Jiangxi Hongdu Aviation Industry GroupCorporation Limited, Nanchang 330024, China)(2.School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China)

Abstract:In a new design of an aircraft wing, the multiple objective decision making is needed. But in selecting training aircraft wings’ airfoils the prior experience is insufficient, so it is needed to further study and conclude the selection rules of the wing airfoil. The airfoils used in training aircraft wings are collected and a method of airfoil selecting for wing design by using rough set theory is provided. Weight reflecting importance of each factor is the key parameter in evaluating or decision-making. The method of weight determining combining the attribute importance with conditional information entropy, which is conformed by conducting a project of trainer wing design, is suitable for airfoil selection in wing design. The number of breaking point in discretization of parameter of airfoil is studied. It is advised that two breaking point method is preferable than one and three, when the number of airfoils in data base available is limited. The method used in this paper is believed to be useful for trainer aircraft wing’s design.

Key words:airfoil; trainer aircraft; rough set theory

作者简介：

中图分类号：V271.6

文献标识码：A

DOI：10.16615/j.cnki.1674-8190.2016.01.012

文章编号:1674-8190(2016)01-087-07

通信作者：魏斌斌,1274724740@qq.com

收稿日期：2015-12-17；修回日期：2015-12-29