数学因变化而灵动

陈建龙

[摘 要]在数学学习中能抓住问题的核心是学生取得成功的关键所在，为了促进学生思维能力的提升，教师的教学应当主动求变，让学生有更多的历练机会，从而使他们学得更轻松。

[关键词]变化 灵动 深度 深刻

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2016）08-083

许多人说“数学是聪明人的思维游戏”，其实很多时候人也会在思维游戏中变得聪明。因此，当学生能从错综复杂的问题中找出关键点，能够抓住问题的核心来思考的时候，学生的数学视野已然开阔，学生的数学思维能力已然形成，学生的数学素养也更上一个新的台阶。从这个角度来看，教师的数学教学不应当墨守成规，而应当积极求变，让学生在广泛的数学思维活动中提升自己的观察能力、总结能力，使学生在数学学习上有更多的收获。

一、变化问题的常态问法，给学生一个深度思考的机会

学生遇到问题时容易陷入思维定式中，只要遇到类似的问题，学生就会调动已有的经验来解决问题，失去了学习的乐趣。因此教师要经常变换练习题的类型，给学生一个深度思考的机会。

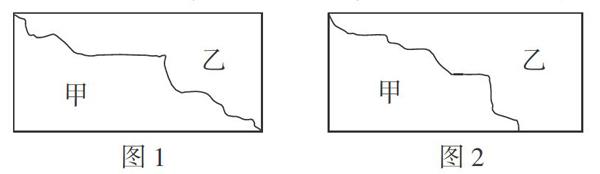
例如，学生在学习“长方形的周长和面积”之后，练习中经常会出现这样的辨析题：如图1所示，甲乙两部分的周长（ ），面积（ ）（在括号内填“相等”或“不相等”）。经过多次的练习后，不管是理解的还是不理解的学生都形成了自然反应：周长相等，面积不相等。因此，我将问题进行改编：如图2所示，甲乙两部分的周长（ ），面积（ ）。果然大部分的学生不假思索地分别填上了“相等”和“不相等”两个答案。在学生交流的环节，有学生指出：图2中甲和乙有一条公共边，甲的周长为公共边加上长方形的一条宽以及一条长的一部分，而乙的周长为公共边加上一条宽和一条长，以及下面一条长的一部分，因此甲的周长较小，再通过观察，清楚地看到甲的面积的也较小。通过分析错误的原因，学生知道自己是因为思维定式，没有认真审题，将不同的题目混淆。

由此，学生告别了“懒惰”，又重新从数学的角度出发去思考问题和辨析问题，从而解决问题。

二、变换问题的呈现方式，给学生一个“亲密接触”的机会

学生的思维能力通常在解题中得到提高，因此，教师在教学中可以变化问题的呈现方式，为学生设置一些障碍，让他们经过自己的探索得到问题的答案。

例如，在教学“认识小数”时，在学生认识了小数部分的数位顺序以及计数单位之后，我请学生思考一个问题：0.45是由（ ）个（ ）组成的。学生的常规解题思路是将0.45中的4和5分开看，得出4个0.1和5个0.01的结论。但问题显然不是这样要求的，所以学生需开动脑筋探寻不同的解题思路。集体交流时，有学生画出计数器来说明问题：0.45就是在十分位上拨出4个珠子，在百分位上拨出5个珠子，要将它们放到一起，可以将十分位上的珠子移到百分位上去，变成40个珠子，共为45个珠子，于是就有45个0.01，甚至有学生提出将这45个珠子移到千分位上去，就会变成450个珠子，所以是450个0.001。以此类推，可以得到无数种不同的答案。学生利用“计数器”，将抽象的解题过程表象化，降低了题目的难度。

在学习的过程中，学生自己去探寻，去尝试，去与问题“亲密接触”，掌握解题的真谛，收获独特的乐趣。

三、变换问题的绝对难度，给学生一个向上突破的机会

有效的数学学习不应当建立在单一问题的简单堆砌上，而应当是层层递进的。当学生的认识随着问题的变化而逐步深入时，他们就会感受到挑战，会激发起继续前行的动力。因此，教师要敢于尝试，敢于突破教材的限制，让学生在拓展学习内容中有进一步的收获。

例如，在教学“认识负数”时，当学生对“负数”的概念有了初步的认识后，我抛给学生一个问题：“在一次体质检测中，小华的坐位体前屈成绩是﹣2厘米，而身高被记为﹣1厘米。他百思不得其解，你能运用所学的知识帮助他解开困惑吗？”学生联系生活实际，猜想“﹣1”应该是相对于某一个标准而言的，可能是全班的平均身高，也可能是该年龄段学生应该达到的标准身高。于是，我揭示了答案：“医生是以全国该年龄的学生的平均身高为准备来记录体侧中学生的身高的。”这个答案引起了学生的广泛共鸣。这样的相对意义上的“负数”给学生的认识提出了更高的要求，让他们更加深刻地体会到“标准”的重要性，为接下来的学习打下了良好的基础。

总之，教师在教学时要不断变化问题的难度和呈现方式，找准切入角度，让学生的思维随之灵动起来，让学生的数学学习真正深入骨髓。

（责编 莫秋鸿）