同中求异,让学生的思维精彩绽放
吴华平
[摘 要]教师往往为了更快完成教学任务,常常一味求同,忽略了个别学生的独特思维,掐灭了学生的思维火花,这样的教学模式是与新课标所提倡的发展学生创新思维这一理念背道而驰的。由一道练习题入手,引导学生思考,让学生的思维精彩绽放。
[关键词]创新思维 同中求异 教学策略
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2016)08-038
在教学“正方体的表面积计算”后,我设计了一道练习题:如图1,小正方体的表面积是16平方厘米,用8个这样的小正方体拼成一个大正方体,求大正方体的表面积。
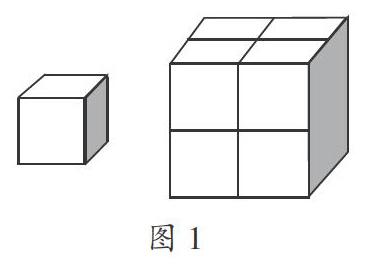
大部分学生都是先求出一个小正方体一个面的面积,再算出大正方体一个面的面积,然后计算出大正方体的表面积。如何求出小正方体一个面的面积?根据正方体表面积等于6个相同的正方形面积之和这一原理,学生求得小正方体一个面的面积为“16÷6=8/3(平方厘米)”,同样的方法,大正方体的表面积等于6个正方形的面积即“8/3×4×6=64(平方厘米)”。
在批改过程中,我发现了这样一个独特的解法“16×4=64(平方厘米)”,我第一感觉就是:“这哪里是在解答,分明就是在凑答案!”恼火之余,我又冷静地思考了一下,发现事实并非如此:“因为大正方体的表面积的确是小正方体表面积的4倍,学生的思路没错!”于是我决定在课堂上展开一次辨析会,听听其他学生的想法。
【教学片段】我让学生说说题目要先求什么,再求什么,最后求什么。学生认为,要先求出小正方体一个面的面积,再求出大正方体一个面的面积,最后再求出大正方体的表面积,并由此列出综合算式为“16÷6×4×6=64(平方厘米)”。我追问:“如果不求小正方体的一个面的面积,能求出大正方体的表面积吗?”
马上有学生提出:“可以先求出8个小正方体的表面积总和,因为它们拼成了大正方体,然后再减去3个隐藏的小正方形的面积,因此可以列式为‘16×8-(16÷6)×3×8’。”有学生立刻反对:“每个小正方体都有一半的面隐藏,一半的面露在外面,不用管那些隐藏的面,只计算露在外面的面就行了,因此可以列式为‘16÷2×8=64(平方厘米)’。”
我继续引导学生思考:“大正方体的表面积和小正方体的表面积有什么关系?你发现了什么?”有学生认为,小正方体的表面有6个小正方形,大正方体的一个面只有4个相同的正方形,由此可以得到大正方体的一个面的面积是小正方体表面积的2/3,大正方体有6个这样的面,因此“2/3×6=4”,由此可以知道大正方体的表面积是小正方体的4倍;有学生认为,小正方体的表面有6个相同的小正方形,大正方体的表面一共有4×6=24个相同的小正方形,可见大正方体的表面积是小正方体的4倍……
一、加强辨析,提升思维深度
在作业批改中,教师只要一见到不符合标准答案的,就会直接判定为错误,并勒令学生立刻改为标准答案。事实上,虽然学生的答案整齐划一,看似掌握了基础知识,其实他们对数学概念的本质并没有深入理解。此时教师要做的就是多问几个为什么,允许学生有不同的想法,加强沟通辨析。在上述案例中,学生对大正方体和小正方体的关系展开了个性化的思考,让学生对大小正方体的表面积之和、大小正方体一个面的大小比较有了深刻的理解,激发了学生的探究热情。
二、多维转化,提升思维广度
数学的本质是要发展学生的思维,让学生学会用数学的眼光看待问题。因而,教师要进行多方面的引导,帮助学生找到问题多元化的解决方案。
如上述案例中,教师让学生用惯用的思维来解答后引导学生找到其他的解决路径:方法一,先求出8个小正方体的表面积总和再减去3个隐藏的小正方形的面积;方法二,只计算露在外面的面就行了,每个小正方体都有一半的面隐藏,一半的面露在外面;方法三,根据大正方体表面积和小正方体表面积的关系。
三、独辟蹊径,提升思维灵活度
数学教学中,学生常会受到定式思维的影响,思维陈旧固化。面对这种情况,教师要抓住时机,带领学生独辟蹊径,培养学生思维的灵活性。
如上述案例中,我让学生转换思路,不求小正方体的表面积,而是根据大正方体和小正方体的关系来求大正方体的表面积,由此打开了学生的思维空间。学生思维逐渐活跃,很快就找到了两者之间的4倍关系,而同样都是4倍,由于每个学生的描述和理解也迥然不同,学生的思维能力在交流讨论中得到了快速提升。
总之,教师要允许学生有不同的思考方法,而且要理性分析,让学生展开辨析交流,同中求异,碰撞出思维的火花,绽放出智慧的花朵。
(责编 童 夏)

