商誉和价格影响需求的易逝品动态定价与广告决策*

李建启， 路立浩

(天津大学 管理与经济学部， 天津 300072)



商誉和价格影响需求的易逝品动态定价与广告决策*

李建启， 路立浩

(天津大学 管理与经济学部， 天津 300072)

摘要：研究需求受价格和商誉共同影响下易逝品动态定价与广告投资策略的联合决策问题。在初始库存确定的情形下，在某待定销售周期内，企业通过投入广告提升自身商誉从而拓宽市场，以企业利润最大化为目标，建立联合最优动态定价及广告投资策略模型。应用庞特里亚金极大值原理，求得不同系统参数下最优动态定价和广告投资策略及最优的销售周期。通过数值算例验证方法的有效性，结合参数灵敏度分析检验系统参数对最优策略的影响并给出相应管理意义。

关键词：易逝品； 库存控制； 动态定价； 动态广告； 商誉； 极大值原理

易逝品作为一类特殊的商品，具有质量不易保障、价值下降迅速、销售期短、需求不确定等特点，其在生活中无处不在，如水果、蔬菜、机票、电子产品等。正是因其特殊性，对易逝品的管理显得尤为重要。商品销售不仅依赖于价格，也会受到非价格因素(如广告、质量、产品包装等)的影响。因此，企业在易逝品销售管理中，为实现自身利润最大化，价格和广告投入决策至关重要。这也是本文的出发点和主要研究内容。

动态定价近年来作为学术界的研究热点已被广泛应用到易逝品的收益管理中。王宏达和汪定伟[1]对季节性商品的定价方法进行了研究。Liu等[2]将温控纳入研究内容，建立易逝品动态定价模型，利用极大值原理求解最优策略，并将其与静态最优策略比较，结果表明动态定价可以为企业带来更多利润。Liu等[3]研究了需求受价格和质量影响下易逝品的动态定价和仓储技术投资决策，利用极大值原理求解最优策略，并设计算法进行数值模拟。Zhang等[4]考虑了包含单个制造商和单个零售商的易逝品供应链中仓储技术投资和动态定价联合决策问题，并通过收益共享和合作投资合同协调供应链。

然而，上述有关易逝品动态定价模型的文献并没有考虑广告在企业收益管理中的重大作用。现今，随着信息技术与互联网科技的发展，广告对消费者决策影响越来越大，也已成为企业扩大商品销量提升自身品牌竞争力的重要手段之一。在Nerlove和Arrow[5]提出著名的Nerlove-Arrow(N-A)模型后，广告研究已取得丰硕成果，国内外有大量相关文献，Feichtinger等[6]、Huang等[7]、Asut和Buscher[8]对广告研究的相关文献作了细致的回顾与归纳。

在易逝品收益管理研究中，也有学者探讨研究了广告投资决策问题。Pal等[9]研究了需求受销售价格、广告和商铺展示库存水平(DSL)共同影响的单项产品的确定性库存系统。Xiong等[10]以随机需求依赖于价格和广告的假设为基础，建立报童模型，联合决策最优价格、广告投入和订货量。Zhang等[11]研究了易逝品供应链中的生产、定价和广告投入决策问题，以及合作广告对渠道效率的影响。

与上述文献不同的是，本文研究了易逝品最优动态定价和广告投入的联合决策问题。不考虑补货情形，在某待决策销售周期内，初始库存水平既定，需求受价格和广告影响，以企业利润最大化为目标建立优化模型，利用庞特里亚金极大值原理，确定最优的动态定价、广告投入和销售周期，并通过数值算例进行分析说明，为企业决策提供参考。

一、基本模型

企业在销售期[0，tf]内销售某种易逝品，tf未知待确定，不考虑补货情形，给定初始库存I0>0，在tf时刻库存为零，且企业在此销售期内进行广告投入。令u(t)和G(t)分别表示t时刻的广告投入和商誉水平。根据Nerlove-Arrow模型，商誉动态衍化方程为

(1)

式中：γ和δ均为正常数；G0>0为初始商誉水平。

需求受价格和广告的影响，其关系表示为

D(G，p)=kG(α-βp)

(2)

式中：k、α、β均为正常数；p为零售价格。价格需满足条件0≤p(t)≤α/β，以保证需求非负。

令I(t)表示t时刻的库存水平。假设库存衰减率为f(I)=θI且θ>0，则库存动态演化方程为

(3)

(4)

根据上述分析，可构建企业最优联合动态定价与广告策略及最优销售周期优化模型，即

(5)

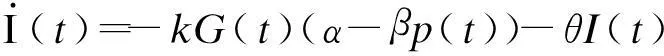
I(0)=I0

I(tf)=0

G(0)=G0

u(t)≥0

二、模型分析与求解

利用庞特里亚金极大值原理求解最优化模型(5)。构建哈密尔顿函数，即

λ1(kG(α-βp)+θI)+

λ2(γu-δG)

(6)

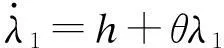
(7)

(8)

并满足横截条件

式中，μ为待定常值。

哈密尔顿极大化条件为

H(I*(t)，G*(t)，p*(t)，u*(t)，λ1(t)，λ2(t)，t)≥

H(I*(t)，G*(t)，p(t)，u(t)，λ1(t)，λ2(t)，t)

(9)

根据式(6)和(9)，可得最优价格和广告投资策略分别为

(10)

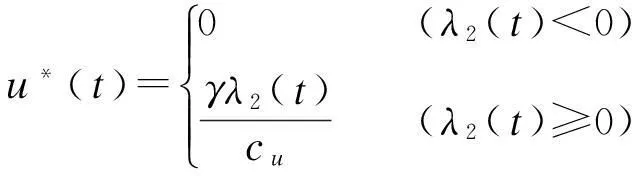
(11)

(12)

其等价于方程

(13)

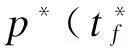
根据终端条件λ1(tf)=α/β，可得微分方程(7)的解为

(14)

(15)

下面给出本文的主要结论：

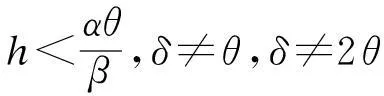
(16)

最优广告投资策略为

(17)

(18)

其中

(19)

(20)

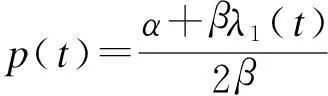
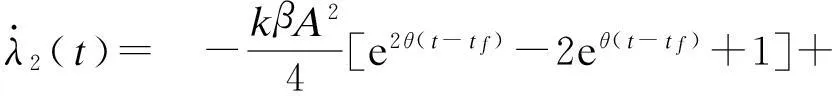
δλ2(t)

(21)

当δ≠θ，δ≠2θ时，根据横截条件λ2(tf)=0可得微分方程(21)的解为

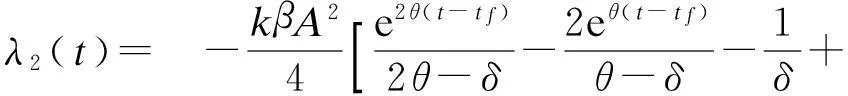
(22)

对式(22)关于t求导可得

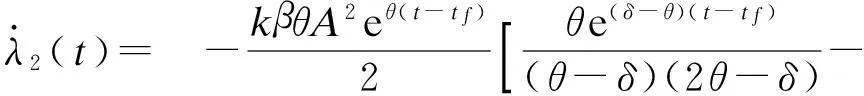
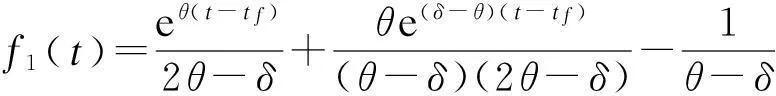
将式(17)代入式(1)，根据初始条件G(0)=G0可得企业商誉水平为

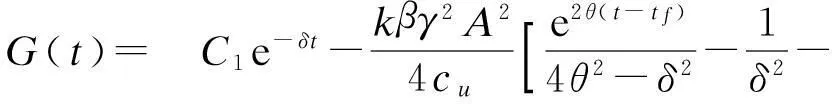
(23)

将式(16)和(23)代入式(3)中，根据初始条件I(0)=I0可得库存水平为

(24)

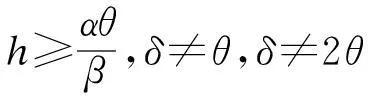
(25)

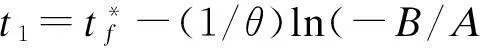
最优广告投资策略为

(26)

(27)

其中

(28)

C7=eθt1(I(t1)-Q(t1))

(29)

其中

当λ1(0)<-α/β，δ≠θ，δ≠2θ时，根据λ1(t)的单调性和式(15)，可得最优的定价策略p*(t)，如式(25)所示。由λ1(t)的单调性可知，存在唯一t1满足方程λ1(t1)=-α/β。

在区间[0，t1]内，将[0，t1]代入式(8)可得

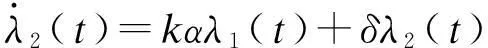
(30)

当δ≠θ且δ≠2θ时，在区间[t1，tf]上λ2(t)的形式与式(22)相同。在区间[0，t1]上，根据终端条件可得

由λ1(t)≤-α/β和λ2(t1)>0可得在区间[0，t1]上λ2(t)>0。综上，最优广告投资策略u*(t)如式(26)所示。

将式(26)代入式(1)，根据初始条件G(0)=G0可得企业的商誉水平为

(31)

其中

(32)

(33)

将式(25)和(31)代入式(3)，根据初始条件I(0)=I0可得库存水平为

注：命题1和2只考虑了参数δ≠θ且δ≠2θ的情形。当δ=θ或δ=2θ时的最优策略可取极限得到，因此本文省略了这部分内容的阐述和证明。

三、算例分析

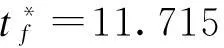
p*(t)=7.5exp(0.1t-1.171 6)+2.5

最优广告策略为

u*(t)=140.62exp(0.1t-1.171 6)(exp(0.1t-

1.171 6)-1)-46.875exp(0.3t-

3.514 7)+46.875

计算可得公司最大利润J*=353.256 7。

系统参数θ、δ和k对最优价格与广告策略及最优销售周期的决策影响重大，为此本文对这些参数进行了灵敏度分析，如图1~3所示，不同产品及商誉衰减系数θ、δ及不同要求对商誉的敏感度k的最优销售周期和利润分别如表1~3所示。

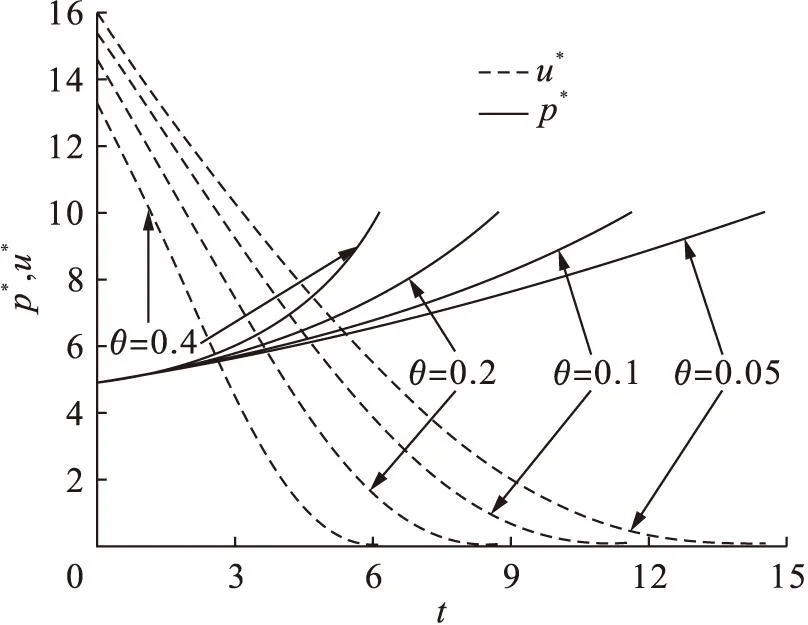
图1　不同产品衰减系数θ下的最优价格与广告投资策略

θt*fJ*0.0514.5757426.23410.1011.7158353.25670.208.7796263.50590.406.1841175.2008

图1和表1显示，产品衰减系数越大，产品的最优销售周期越短，最优价格越高，企业的广告投资越低。较高的衰减系数促使企业在较短的销售周期内销售产品，并降低广告投资提高价格以减少成本与损失。衰减系数越大，价格增长速度越

图2　不同商誉衰减系数δ下的最优价格与广告投资策略

δt*fJ*0.0510.0551562.62880.3011.7158353.25670.4012.9501214.03120.5014.242880.1980

快，广告投资下降速度越慢。表1表明，产品衰减系数越大企业利润越小。

图2和表2显示，商誉的衰减系数越大，销售周期越长，产品的销售价格越低，在销售周期初期广告投资越低，在销售周期中后期投入广告越高。商誉衰减系数越大，价格增长速度越慢，广告投资下降速度越慢。表2表明，商誉衰减系数越大企业获得的利润越低。

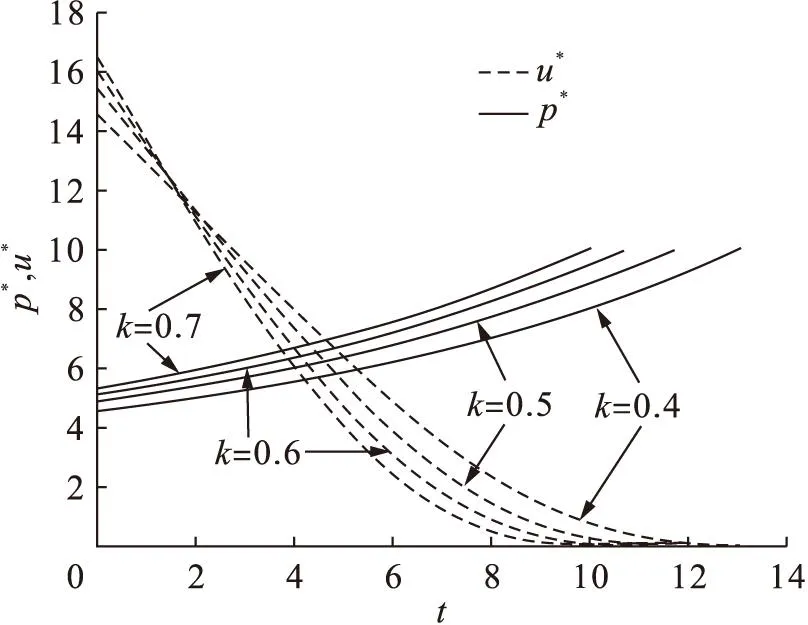
图3　不同需求对商誉的敏感度k下的

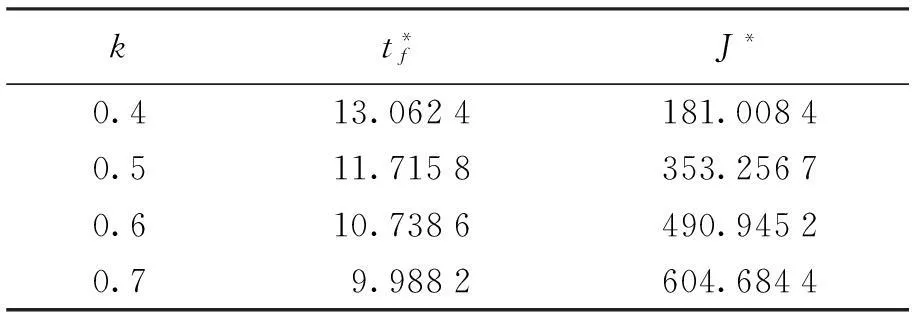
kt*fJ*0.413.0624181.00840.511.7158353.25670.610.7386490.94520.79.9882604.6844

图3和表3显示，商誉对需求影响系数越大，产品的销售周期越短，产品相应的销售价格越高，在销售周期初期广告投资越高，销售周期后期广告投资越低。需求对商誉的敏感度越大时，相同价格时需求则越大，因此企业有更大的定价空间，从而提高企业收益。需求对商誉的敏感度越大时，企业在初期广告投资越多以迅速扩大销量并减少商品自身衰减的损失，而在中后期提高商誉水平可缩减广告投资以减少成本，同时提高价格获得更高利润。需求对商誉的敏感度越大时，价格增加速度越快，广告下降速度越快。表3表明，需求对商誉的敏感度越大企业获得的利润越高。

四、结论

本文研究了价格与商誉同时影响需求下，易逝品的最优动态定价与广告投资策略以及最优销售周期决策问题。应用庞特里亚金极大值原理，得到不同系统参数下企业利润最大化的最优动态定价与广告策略及相应的最优销售周期。通过数值算例和系统参数灵敏度分析对企业最优动态定价与广告策略及最优销售周期进行深入分析和研究，为企业采取动态定价与广告策略运营策略提供技术支持。

本文只考虑了易逝品单周期的动态定价与广告投资策略问题，而多周期销售行为在生活中也比较常见，该情况下的动态定价与广告投资策略问题有待进一步研究。消费者行为对企业的运营销售策略具有重要的影响，在研究产品运营策略时可以将消费者行为(如参考价格)考虑进来，这将是一项极富挑战性的任务。

参考文献：

[1]王宏达，汪定伟.季节性商品的定价模型及方法研究 [J].沈阳工业大学学报，2005，27(5)：579-581.

[2]Liu W W，Tang W S，Feng L，et al.Dynamic pricing under temperature control for perishable foods [J].Journal of Systems Science and Systems Engineering，2014，23(3)：252-265.

[3]Liu G W，Zhang J X，Tang W S.Joint dynamic pricing and investment strategy for perishable foods with price-quality dependent demand [J].Annals of Operations Research，2015，226(1)：397-416.

[4]Zhang J X，Liu G W，Zhang Q，et al.Coordinating a supply chain for deteriorating items with a revenue sharing and cooperative investment contract [J].Omega，2015，56(10)：37-49.

[5]Nerlove M，Arrow K J.Optimal advertising policy under dynamic considerations [J].Economica，1962，29(114)：129-142.

[6]Feichtinger G，Hartl R F，Sethi S P.Dynamic optimal control models in advertising：recent development [J].Management Science，1994，40(2)：195-226.

[7]Huang J，Leng M M，Liang L P.Recent developments in dynamic advertising research [J].European Journal of Operational Research，2012，220(1)：591-609.

[8]Aust G，Buscher U.Vertical cooperative advertising and pricing decisions in a manufacturer-retailer supply chain：a game-theoretic approach [J].European Journal of Operational Research，2014，223(2)：473-482.

[9]Pal A K，Bhunia A K，Mukherjee R N.A marketing-oriented inventory model with three-component demand rate dependent on displayed stock level [J].Journal of the Operational Research Society，2004，56(1)：113-118.

[10]Xiong Z K，Peng Z Q，Xiong Y U.Joint determination of pricing，order quantity and advertising investment for perishable goods [J].Industrial Engineering and Management，2009，14(2)：32-37.

[11]Zhang J X，Li J Q，Lu L H，et al.Supply chain performance for deteriorating items with cooperative advertising [J].Journal of Systems Science and Systems Engineering，2015(3)：1-27.

(责任编辑：吉海涛)

Dynamic pricing and advertising decision of perishable item with goodwill-and-price-dependent demand

LI Jian-qi, LU Li-hao

(College of Management and Economics, Tianjin University, Tianjin 300072, China)

Abstract：The joint decision problem is studied of dynamic pricing and advertising decision of perishable item with demand influenced by price and goodwill. The model of joint optimal dynamic pricing and advertising investment strategy is established under the conditions that the initial inventory is defined, the sales period is predetermined, the enterprise can expand the market by putting into advertising to enhance its goodwill, and the aim is maximizing profit. The optimal dynamic pricing and advertising investment strategy and the optimal sales cycle are obtained under different system parameters by applying Pontryagin maximum principle. The validity of the model is verified through numerical example method. The influence of system parameters on the optimal strategy is analyzed combining parameter sensitivity analysis, and the corresponding management significance is also given.

Key words：perishable item; inventory control; dynamic pricing; dynamic advertising; goodwill; maximum principle

中图分类号：F 714.1； F 713.8

文献标志码：A

文章编号：1674-0823(2016)01-0085-06

doi：10.7688/j.issn.1674-0823.2016.01.14

作者简介：李建启(1992-)，男，安徽亳州人，硕士生，主要从事控制理论及动态定价等方面的研究。

基金项目：国家自然科学基金面上项目(473204)； 教育部人文社会科学基金项目(14YJCZH204)。

收稿日期：2015-10-28

*本文已于2015-12-24 15∶02在中国知网优先数字出版。 网络出版地址： http：∥www.cnki.net/kcms/detail/21.1558.C.20151224.1502.022.html