拖拉机离合器压盘的热应力分析研究
胡东方,杜艳平,李 鹏
(1.河南科技大学 机械工程学院,河南 洛阳 471003; 2.洛阳中收机械装备有限公司,河南 洛阳 471003)
拖拉机离合器压盘的热应力分析研究
胡东方1,杜艳平1,李鹏2
(1.河南科技大学 机械工程学院,河南 洛阳471003; 2.洛阳中收机械装备有限公司,河南 洛阳471003)
摘要:在温度场影响下,拖拉机离合器压盘在使用过程中常出现热烧蚀、热开裂等问题,大大降低了离合器总成的使用寿命。为解决上述问题,通过测绘φ280离合器压盘实物,在SolidWorks中,建立了完整的压盘实体模型,通过图形设备接口将其导入到了ABAQUS软件中,建立了有限元模型,经过热应力耦合分析计算得出压盘在滑磨过程中的受热及受力情况。同时,根据分析结果对压盘的结构进行了改进设计,得出了合理的压盘设计方案。结果表明:改进后的压盘轴向变形量降低了6.9%,应力峰值降低了11.96%。
关键词:拖拉机;离合器;压盘;热应力;有限元分析
0引言
随着种植农艺结构的不断升级及农业现代化的发展,用户对拖拉机的整体性能提出了更高的要求。离合器作为拖拉机传动系的重要组成部分,其性能的好坏直接影响到拖拉机能否正常工作。压盘作为离合器的重要工作零件,在离合器接合过程中产生的高温导致热变形,进而对离合器的性能产生很大的影响,因此有必要对压盘进行热应力分析。
由于压盘温度场属于瞬时热源下的热传导问题,其传热过程比较复杂且压盘形状不规则,所以采用传统的热传导方程计算十分困难[1]。随着计算机技术和应用软件技术的快速发展,有限元分析的方法在解决实际问题、新产品的研制和开发中应用得越来越广泛。很多学者已经对离合器压盘的热应力问题进行了大量的研究[2]。本文在前人研究的基础上,在SolidWorks中建立了压盘的几何模型,导入到ABAQUS有限元分析软件中,模拟拖拉机离合器压盘实际工况,对其进行了有限元分析研究,最后得出了压盘的温度场、应力分布及变形情况;同时,对压盘进行改进设计,得出了更合理的压盘设计方案,为压盘和离合器总成的设计和改进提供了参考。
1热应力分析的基本原理
传热学是研究不同温度物体之间或同一物体不同部分之间热量传递规律的学科。所有热量的产生、传递及吸收在整个传热过程中都遵循热力学第一定律,即在热力系统内物质的能量可以通过多种形式进行传递和转移,但是所有形式的能量总和在整个系统中保持不变。能量的转化和转移过程一般通过热传导、热对流和热辐射及3种形式的组合来实现。
求解热应力时,首先需要确定其温度场。一般的求解步骤是首先由边界条件和热传导方程求出初始分布的温度场,然后由热力学方程求出相对应的位移和热应力场。在热量转化过程中,所有类型的热传导过程都遵循能量守恒定律,所以在3种类型的热量转化过程中,也必然遵循能量守恒定律。因此,为得到求解温度场分布的导热微分方程[3],可将能量守恒定律和傅里叶定律相结合,得到的导热微分方程可分为以下3种情况:
1)常物性、无内热源三维非稳态导热微分方程。
2)常物性、稳态有内热源的三维导热微分方程。
在数学上,上式又称为泊桑(Poisson)方程。
3)常物性、稳态、无内热源的三维导热微分方程。
该方程又叫拉普拉斯(Laplace)方程。
式中t—温度;
τ—时间;
a—热扩散率,又称导温系数;
x,y,z—求解点坐标值;
λ—热传导系数,即热导率;
Φ—内热源强度,即单位时间、单位体积的生成热。
2压盘有限元分析计算
2.1热分析平衡方程
离合器压盘的热应力问题属于瞬态传热问题。对于瞬态传热的温度场,系统的温度、边界条件、热流率及系统内能都随随时间变化的。于是,根据能量守恒原理,瞬态热平衡方程可以表示为
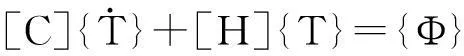
式中[H]—热传导矩阵(包含导热系数、对流换热系数、辐射率及形状系数);
[C]—比热矩阵(考虑系统内能的增加);
{T}—节点温度向量;

{Φ}—节点热流率向量(包含热生成)。
2.2建模及参数获取
根据压盘的尺寸参数,在SolidWorks软件中建立φ280离合器压盘的几何模型,将几何模型输出为x-t形式,输入到ABAQUS分析软件中;网格划分时采用四面体热应力耦合单元C3E4T,单元大小设置为2mm。划分网格后模型的单元总数为651 230个,节点总数为124 895个。压盘的有限元模型如图1所示,分析采用mm/tonne/s单位制。常温或温度变化不大的情况下,压盘的各项材料属性可认为不变或变化很小可忽略不计[4]。离合器压盘的尺寸及材料属性参数如表1所示。

图1 压盘有限元模型
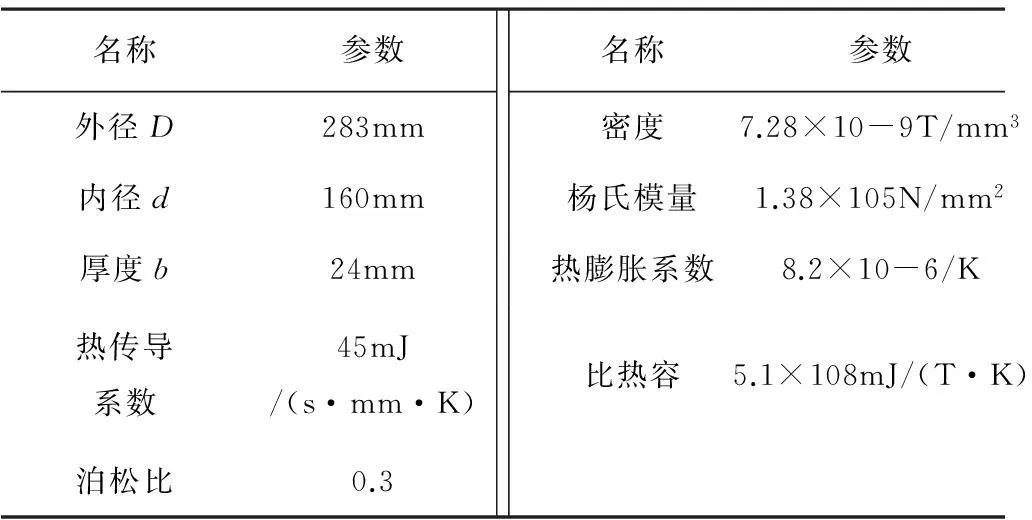
名称参数名称参数外径D283mm内径d160mm厚度b24mm热传导系数45mJ/(s·mm·K)泊松比0.3密度7.28×10-9T/mm3杨氏模量1.38×105N/mm2热膨胀系数8.2×10-6/K比热容5.1×108mJ/(T·K)
2.3压盘的工况仿真
本文模拟的工况为拖拉机正常使用情况下的一般载荷工况。在离合器接合过程中,压盘和从动盘之间产生的滑磨功转化为热量,导致摩擦面温度的变化。在一般载荷工况下,离合器滑磨功为
式中ωε—拖拉机起步时发动机的角速度;
β—后背系数;
I1—拖拉机发动机当量旋转质量的转动惯量;
I2—当量旋转质量转换到离合器轴的转动惯量。
把ωε=230.38rad/s,β=2.31,I1=1.76×103t/mm2,I2=0.64×103t/mm2带入公式,经计算可得滑磨功W=2.1962×107mJ。
根据经验,离合器结合时间为2.05s,分离时间为1s。本文采用直接耦合单元Coupled Temperature-Displacement对压盘进行热应力耦合分析。模拟离合器的结合工况,设定析步step combination为2.05s,模拟分离工况,设定分析步step separation为1s。
2.4边界条件的设置
2.4.1位移约束条件
由于被碟形弹簧压紧,故离合器压盘受碟形弹簧压住的部分可近似按刚性约束处理,即其轴向位移为0。对于压盘上外沿的3个安装传动片的孔在圆周切线方向也不存在相对位移,所以也按刚性条件处理,限制其径向和圆周切线方向的位移。
2.4.2初始化温度边界条件
初始化温度条件为
式中x,y,z—测试点的坐标值;
t—时间;
T0—环境温度。
分析时,假定接合时的瞬间环境温度为压盘温度,即初始化温度T0=30℃,在ABAQUS软件的预定义场中将此温度场作为初始边界条件施加在压盘表面。该温度场不是定值,它将随着离合器的工作过程而发生变化。
2.4.3对流换热边界条件
对流换热即相对运动着的流体与温度不同的固体接触时流体与固体壁面之间由于温差而出现的热量交换现象。离合器工作时,由滑磨产生的摩擦热使压盘温度升高,进而与周围流体(空气)发生对流换热,一般用对流换热系数来表示。对流换热系数在离合器工作过程中是变化的,因此本文对对流换热做了如下简化:①其特征速度用离合器压盘内、外径的平均速度表示; ②分别计算出26.85℃~362.85℃之间每间隔50℃的对流换热系数,再用插值函数写出随温度变化的曲线方程,近似地得到瞬时对流换热系数[5]。压盘表面的对流换热系数可由对流换热系数计算公式计算得到,则
式中λ—空气导热系数;
D—特征尺寸;
Re—雷诺数。
将数据带入对流换热系数公式,得出的结果如表2所示。

表2 对流换热系数表
结合工况时,压盘和摩擦片紧密结合,因此在step combination分析步骤中不存在对流换热,不需要设置对流换热系数;当离合器进入分离工况时,再在step separation分析步骤中将对流换热边界条件施加到摩擦面上。
2.5热流密度边界条件
热流密度也称热通量,是一种面载荷,表示单位面积截面内单位时间通过的热量。在离合器工作过程中,假设压盘和摩擦片吸收了所有的热量,则t时刻距离压盘圆心r1处的热流密度为
式中W—滑磨功;
R—压盘外径;
r—压盘内径。
将W=2.1962×107mJ,t0=2.05s、R=141.5mm、
r=82.5mm带入热流密度计算公式,可得压盘和摩擦片之间产生的热流密度为q=4.508r(1-0.488t)。这部分热流将分配给摩擦元件级即压盘和摩擦片。
为了计算被压盘吸收的热流密度qy,需引入热流分配系数[6]的概念,它表示离合器压盘和摩擦片之间因摩擦产生的摩擦热分配在压盘和摩擦片上的比值。热流分配系数可由下式求得,则有
式中λ—导热系数;
c—比热;
ρ—密度。
带入材料参数,计算可得k=11.6。由于本研究采用的是单片摩擦片式离合器,因此分配到压盘上的热流密度为
将k带入上式,可得压盘热流密度qy=4.234r(1-0.488t)。由此可以看出:由于摩擦片材料本身导热性不好,大部分热量被压盘吸收。该热流密度可利用ABAQUS中的Analytical Fields和Amplitudes进行加载。由于离合器分离时压盘和摩擦片不存在接触,因此需在step separation中将热流密度解除。
3压盘有限元仿真结果分析
将所建立的有限元模型提交ABAQUS进行热应力分析和后处理之后,可在后处理可视化模块中进行观察分析。
3.1温度场分布结果分析
由图2可以看出:最高温度出现在压盘摩擦面外缘处,其节点编号为4411,最高温度为65.34℃,出现在离合器结合1.071s的时候。在2.05s滑磨结束时,压盘的最高温度为57.52℃。压盘最大温度出现在离合器结合终了前的某一时刻而不是接合终了时刻,这是由于在滑磨结束时刻两摩擦元件的角速度逐渐趋于一致,滑磨功逐渐降低, 热传导和对流换热带走的热量[7]要大于摩擦产生的热量。在整个过程中,最大温升为35.34℃。

图2 温度场峰值云图
图3为压盘摩擦表面径向的7个节点的温度变化曲线。在压盘的结合过程中,摩擦表面径向温度变化趋势一致,温度先急剧升高后缓慢下降。这是由于压盘与空气之间的换热时间太短,在离合器压盘和摩擦片刚开始结合时,滑磨功急剧变大,导致温度急剧升高;在结合后期,压盘和从动盘角速度趋于一致,滑磨功大大降低,热传导和热对流换热带走的热量大于摩擦产生的热量,因此温度开始下降;离合器进入分离工况后,摩擦作用消失,热传导和热对流带走的热量使得压盘温度进一步降低。温度随着半径的增加在变高是由于摩擦面上的热点相当于瞬时热源,滑磨线速度与半径成正比。图4为压盘外端面轴向7个节点的温度变化曲线。在轴向上,温度的变化主要是因为压盘内部热传导和与空气的对流换热作用,主要表现为:节点温度在远离摩擦面的方向上逐渐降低;靠近滑磨表面的节点,温度变化趋势与滑磨表面节点相似,即温度先快速升高后缓慢下降;而距离滑磨表面较远的节点温度则近似成单调增加的趋势。
3.2应力场结果分析
由图5可以看出:压盘的热应力分布相当不均匀。由于接合时间较短,热量产生的速度远远大于材料内部热传导速度,因此压盘在径向上的温度变化梯度高于轴向温度变化梯度,从而导致径向应力大于轴向应力,因此热裂纹往往是沿径向分布。从分析的整个过程来看,Von Mise等效应力变化滞后于温度,最高温度发生在离合器结合1.071s时,而应力峰值在离合器结合1.539s时才出现。由此认为,热应力的产生是由温度不均所致。等效应力最大值达到144.6MPa,出现在压盘安装孔内的某一点。这是由于“凸耳”存在,在“凸耳”处热传递和对流换热带走了一部分热量,导致此区域温度降低,但附近区域又是线速度最高的高温区,结果导致此处的温度梯度最大,并在安装孔附近出现了比较明显的应力集中现象。

图4 轴向节点温度变化曲线

图5 应力峰值云图
3.3变形分析
由图6可以看出:压盘的热变形沿径向的变形由内向外逐渐增大,整个压盘的变形表现为径向膨胀、轴向翘曲,成“碟状”。滑磨表面外缘部分线速度高,产生的滑磨功大、温度高,因此变形量大,翘曲量达到0.037 84mm;但在“凸耳”处,由于安装孔处约束的存在,有效地控制了压盘沿径向的膨胀;在轴向上,由于温度梯度变化不均,导致压盘外缘翘曲变形的不均,从而加剧滑磨表面局部磨损,影响压盘的使用寿命。

图6 变形云图
4压盘结构改进及分析
通过前面的分析可知:压盘在结合过程中温升现象较明显,应力分布集中,轴向翘曲比较严重。为此,本研究从压盘的结构和散热等方面提出了如下的改进措施:①将原来水平的上表面改成了斜坡形,起到加强筋的作用,从而可使压盘的轴向翘曲现象得到一定改善;另外,该改变在原来结构的基础上质量有一定的增加,可以适量增加一部分散热。②将原结构摩擦面的内锥度增加到1°,内锥度会使离合器工作过程中摩擦面积增大,减轻压盘轴向变形引起的摩擦面减小的现象。改进前后结构如图7所示。
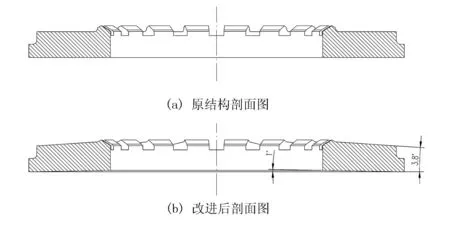
图7 改进前后结构对比
为了检验改进后的效果,对新的结构进行了条件不变的热应力耦合分析。新结构的温度变化曲线和原结构的相似。图8~图10为改进后结构的温度峰值云图、应力峰值云图和最大变形云图。其温度峰值为65.28℃,与改进前相比,降低得比较小,几乎可以忽略不计;但是滑磨表面的温度场分布有了一些变化,其最高温度在向“凸耳”处靠近;应力最大值为127.3MPa比原结构降低了11.96%,有了明显的下降,但应力集中现象依然明显。然而,由于应力的减小及压盘上表面结构的改变,使对压盘滑磨影响比较严重的轴向变形量下降了6.9%,由原来的0.033 53mm变为0.031 2mm,轴向翘曲现象有了一定的改善。表3为结构改进前后有限元分析结果的对比。由表3可知:新结构要优与原结构,改进后温度峰值降低了0.12%,应力峰值降低了11.96%,轴向变形量降低了6.9%。

图8 改进后温度峰值

图9 应力峰值

图10 变形云图
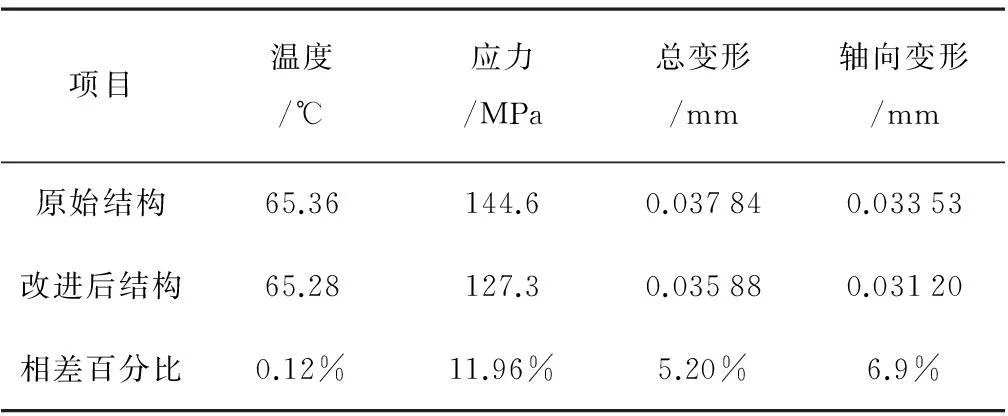
项目温度/℃应力/MPa总变形/mm轴向变形/mm原始结构65.36144.60.037840.03353改进后结构65.28127.30.035880.03120相差百分比0.12%11.96%5.20%6.9%
5结论
1)压盘温度峰值为65.36℃,发生在滑磨过程中的某一时刻,而不是在滑磨结束的时刻;且温度场分布不均,随着半径的增加在增高,高温区集中在摩擦面上。轴向方向存在明显的温度梯度,温度在远离摩擦面的方向上逐渐降低。应力的变化滞后于温度,其应力峰值为144.6MPa,发生在安装孔内,整个压盘应力集中现象明显。位移峰值为0.037 84mm,出现在滑磨表面两“凸耳”之间的外缘处,整个压盘发生明显的翘曲变形。
2)为改善拖拉机压盘的受热变形情况,本研究对压盘结构进行了改进。将原来的平的上表面改成了3.8°的斜坡面,原来摩擦面的内锥度增加到1°。分析结果表明:改进后的压盘的应力、变形量有比较明显的降低,有效地降低了应力集中,减小了翘曲变形,使压盘的可靠性有一定的提高。
参考文献:
[1]朱茂桃, 张铁山. 离合器压盘表面工作温度变化规律的测定[J].江苏理工大学学报,1996,17(2):32-36.
[2]张凡, 鲍际平. 重卡离合器压盘热应力有限元分析与改进[J].林业机械与木工设备,2011,39(4):23-26.
[3]许国良.工程传热学[D].武汉:华中科技大学,2010.
[4]高翔, 徐阳. 轿车起步工况离合器压盘热-机耦合分析[J].重庆交通大学学报:自然科学版,2014,33(3):149-154.
[5]郭孝文, 张丽平. 客车摩擦式离合器的热工况分析及其改善措施[J].机电技术,2014(1):77-80.
[6]刘雪莱,朱茂桃.离合器压盘热负荷特性分析及改进研究[J].机械传动,2014,38(5):128-131.
[7]陆锋,朱茂桃,刘雪莱.离合器压盘瞬态热分析与结构改进[J]. 交通科学与工程,2013,29(2):94-97.
Thermal Stress Analysis of Tractor Clutch Pressure Plate
Hu Dongfang1, Du Yanping1, Li Peng2
(1.Henan University of Science and Technology, School of Mechatronics Engineering, Luoyang 471003, China; 2.Luoyang Zhongshou Machinery & Equipment Co.Ltd.,Luoyang 471003,China)
Abstract:Thermal ablation, thermal cracking and other problems often appear during the use of tractor clutch pressure plate, which greatly reduces the service life of the clutch assembly. To solve the problem above, complete platen solid model was established in Solidworks by mapping the φ280 clutch pressure plate. Then the finite element model is established by means of importing it into the software of ABAQUS using the ABAQUS and Solidworks interface. After thermal stress coupling analysis the heat and stress conditions of the pressure plate was calculated .According to the analysis result ,the structure of the pressure plate is improved and the rational design was obtained . The results show that: the axial deformation of the improved pressure plate decreased 6.9% and it’s stress peak decreased 11.96%.
Key words:tractor; clutch; pressure plate; thermal stress; finite element analysis
文章编号:1003-188X(2016)04-0231-06
中图分类号:S219.03
文献标识码:A
作者简介:胡东方(1967-),男,河南洛阳人,副教授,硕士生导师,(E-mail)hdf@haust.edu.cn。
基金项目:国家自然科学基金项目(61070247 );河南省教育厅科技攻关项目(13A520232 )
收稿日期:2015-03-31

