双偏心卵形齿轮行星系分插机构的分析研究
谈梅兰,周 涛,沈 燕,华希俊
(1.江苏大学 a.力学与工程科学系;b.机械工程学院,江苏 镇江 212013;2.江苏大学 常州工程技术研究院,江苏 常州 213164)
双偏心卵形齿轮行星系分插机构的分析研究
谈梅兰1a,周涛1a,沈燕2,华希俊1b
(1.江苏大学 a.力学与工程科学系;b.机械工程学院,江苏 镇江212013;2.江苏大学 常州工程技术研究院,江苏 常州213164)
摘要:鉴于已有的高速水稻插秧机中的椭圆齿轮行星系分插机构在取秧过程中易出现伤秧、插秧过程中易出现倒秧或插不进秧的情况,借助于计算机辅助软件对双偏心卵形齿轮行星系在高速水稻插秧机旋转式分插机构上进行了应用研究,提出了以标准卵形齿轮节曲线和标准直齿圆柱齿轮渐开线作为基础,对无函数表达式节曲线的双偏心卵形齿轮行星系各项参数进行理论分析,建立双偏心卵形齿轮行星系的实体模型,为了将其与插秧机上其他零部件进行装配,给出了双偏心卵形齿轮行星系旋转式分插机构虚拟制造结果。对改装后的插秧机分插机构的虚拟样机进行仿真,与椭圆齿轮行星系分插机构在插秧性能方面进行比较。结果表明:由于双偏心卵形齿轮相对于标准椭圆齿轮的设计变量多,因而结构优化更灵活,安装在插秧机上稳定性好。因此,双偏心卵形齿轮行星系分插机构比椭圆齿轮行星系分插机构更能满足在高速化条件下插秧轨迹的要求。
关键词:高速水稻插秧机;双偏心卵形齿轮行星系;分插机构;虚拟制造
0引言
随着我国农业机械化总体水平的提高,水稻生产机械化程度也取得了长足进步。但是,我国水稻生产机械化水平与发达国家相比还是有些落后,必须对水稻栽植机械化进行不断创新。
1非圆齿轮节曲线传动理论
任意非圆齿轮节曲线如图1所示。设主动轮1的转角为φ1、瞬时角速度为ω1,从动轮2的转角为φ2、瞬时角速度为ω2。在起始位置,φ1=φ2=0,要求齿轮副传递转角函数关系为φ2=F(φ1),则齿轮副的传动比函数表示为[8]
(1)

(2)
则从动轮2节曲线方程为
(3)
为了保证齿轮副作单向连续转动,以传递周期性运动关系,两齿轮节曲线都应该是封闭的,即
(4)
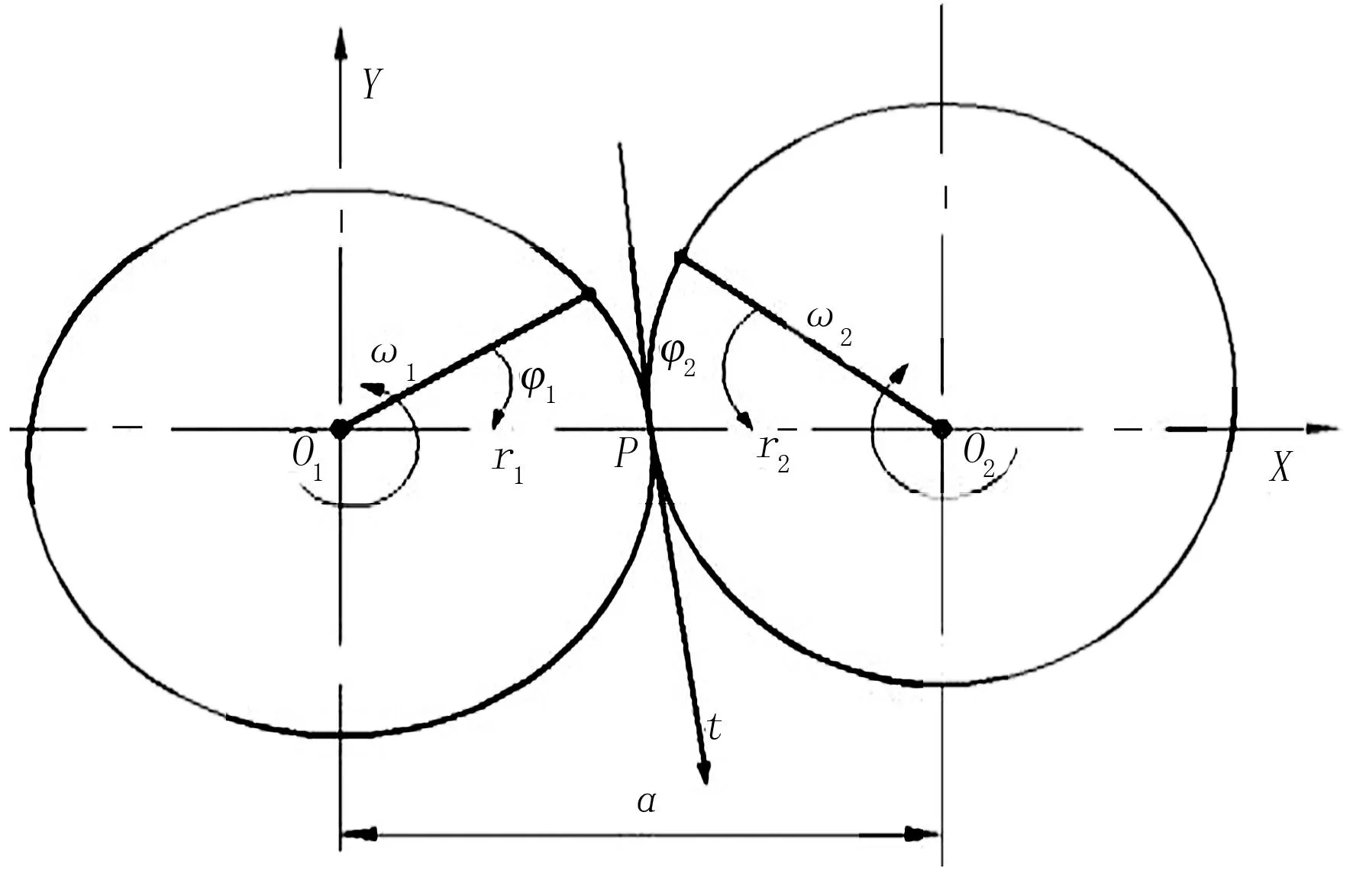
图1 非圆齿轮节曲线
2双偏心卵形齿轮行星系参数设计
所谓双偏心卵形齿轮是转动中心在标准卵形(二阶椭圆形)齿轮的长轴(X轴)和短轴(Y轴)的两个方向上都有一个偏移量,以偏移后的转动中心为基准形成的齿轮如图2所示。
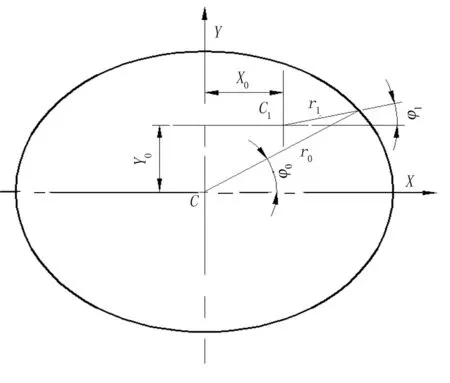
图2 双偏心卵形齿节曲线设计示意图
2.1双偏心卵形齿轮行星系节曲线设计
图2中,C点为标准卵形齿轮的回转中心,C1点为双偏心卵形齿轮的回转中心, 偏心量用坐标值表示为(X0, Y0),r0与r1分别是两种不同齿轮节曲线上点的极半径,而φ0与φ1则分别是相应的极角。
标准卵形齿轮节曲线方程为
(5)
其中,A为标准卵形齿轮节曲线长轴半径;e为离心率。由图2可列出方程为
(6)
这样就可给出双偏心卵形齿轮节曲线的极半径和极角方程,即
(7)
双偏心卵形齿节曲线的周长为
(8)
根据已有的标准椭圆齿轮行星系的中心距a=42.25mm、齿数Z=20,初定X0= 0.03mm、Y0=2.58mm。 利用MatLab软件,联立式(4)、式(5)、式(7)和式(8),计算得到A=19.992mm,e=0.028, 代入式(5)得标准卵形齿轮节曲线方程r0(φ0)。同时,式(7)给出了双偏心卵形齿轮主动轮节曲线方程,与之啮合的共轭齿轮的节曲线方程也可利用式(7)的结果,并借助于式(3)推得,此处不再赘述。
2.2双偏心卵形齿轮的齿廓设计
双偏心卵形齿轮可以用齿条型刀具或插齿刀加工,其齿高、齿距、齿厚等一系列计算方法如表1所示。齿轮齿廓设计是齿轮设计中的难点,特别是非圆齿轮的齿廓更为复杂。基于此类难点并结合表1的基本参数,提出一种简单、精确的轮廓线设计方法。

表1 齿轮设计公式

续表1
这里需要建立两套坐标系:整体坐标系OXY和基于每一个齿的局部坐标系Oxy,其中的原点O就是图2中的C1点,如图3所示。

图3 双偏心卵形齿轮设计算法示意图
由于双偏心卵形齿轮节曲线不是圆,节曲线上各点曲率半径不一样,为此提出以标准圆柱齿轮齿廓方程为基础,通过运用二分法、无约束优化方法和坐标变换等,利用MatLab软件近似优化出双偏心卵形齿轮齿廓。
设计思路及过程概要如下, 其中给出的一些确定的数据是由大量的设计经验积累确定的。
1)按齿数等分节曲线总长后,建立目标函数,使

(9)
调用二分法[9]求每个等分点所对应的弧度βi(I= 1, 2, …,Z),如图3(a)所示。
2)建立目标函数,使
(βi+0.02<βLi<0.99βi+1)
(10)
(βi-1+0.02<βRi<0.99βi)
(11)
运用步骤1)的方法求等分点左、右两侧渐开线与节曲线的交点分别对应的弧度βLi和βRi,见图3(a)。而交点对应的极径rLi和rRi可利用公式(7)求r1的方法求得。
3)求左、右渐开线与节曲线的交点的曲率半径ρLi和ρRi,以及曲率中心坐标(XρLi,YρLi)、(XρRi,YρRi),具体公式见表1。
4)求左、右初始渐开线在局部坐标系下的偏转角度值θLi和θRi,以及初始坐标值(xLi,yLi)、(xRi,yRi)。在第i齿的局部坐标系Oxy下[见图3(b)],以齿的右侧渐开线为例,θRi是渐开线从起点A到其与节圆的交点B的偏转角度值,xRi是交点B的横坐标值,因极半径OB的极角很小,一般保持在1°,所以可近似认为xRi=ρRi,建立目标函数,使
(0<θRi<π/4)
(12)
调用MatLab中fminbnd无约束优化[10]的方法,近似优化出θRi。左渐开线初始偏转角的值θLi可用类似方法求。
这样仿照圆柱齿轮的渐开线方程[11],可有右渐开线参数方程,即
(13)
左渐开线的参数方程可类似地给出,不再赘述。
5)由于上述渐开线方程是建立在局部坐标系下的,所以需要进行坐标变换。坐标变换时偏转角度的权重系数设为qRi和qLi,根据设计经验,取
(14)
建立目标函数,使
rRicosβRi-(XρRi+xRicosγRi+xRisinγRi)=0
(15)
选用合适的上下限,调用零点定理,可以求得γRi,γLi可用类似方法求得。
6)求整体坐标系OXY上的双偏心卵形齿轮左、右渐开线参数方程。右侧渐开线的参数方程可表示为
(16)
由于过渡曲线方程较为复杂,在此对齿根圆角半径采用国家标准r= 0.38mm得近似的过渡曲线。
2.3双偏心卵形齿轮行星系模型建立
经以上理论分析,并通过MatLab编程计算出双偏心卵形齿轮行星系各项数据,在SolidWorks[12]中使用命令:“插入”→“曲线”→“通过XYZ点的曲线”,将齿轮设计的各项数据导入,通过“转换实体引用”,“裁剪”“拉伸”等命令生成实体,最后在装配环境下生成双偏心卵形齿轮行星系实体图,如图4所示。各个齿轮之间的定位关系主要依据齿轮上的铸造标记点,参照原点和竖条的定位关系既可完成正确的定位。至此,双偏心卵形齿轮行星系设计过程完毕。

图4 双偏心卵形齿轮行星系装配图
3分插机构的模拟仿真
3.1结构特点和工作机理
在SolidWorks中将双偏心卵形齿轮行星系与旋转式分插机构其他零部件进行装配,如图5所示。
双偏心卵形齿轮系分插机构齿轮传动部分[13]由太阳轮、中间轮和行星轮组成。行星架与太阳轮同轴,栽植臂固定在行星轮上。工作时(以一侧为例),太阳轮固定不动,行星架绕回转中心转动,中间轮绕太阳轮转动。由于是非圆齿轮啮合,从而引起传动比非匀速变化,使得行星轮相对于行星架作非匀速转动。行星轮一方面随着行星架绕回转中心作圆周运动(牵连运动是定轴转动),同时相对于行星架作非匀速转动,所以栽植臂的运动也就自然成为这两种运动的复合运动。凸轮驱动轴固定在行星架上带动凸轮做平面运动,凸轮和连接臂相连,推秧杆通过连接销同连接臂相连,在复合运动作用下,通过调整一些参数之间的关系(例如插值臂箱体长轴与水平线间夹角的定位关系)和结构参数,秧针就会按照要求的运动轨迹实现取秧、送秧、推秧、回程等不同的插秧动作。

1、7.行星轮 2.植臂输入轴 3、5.中间轮
3.2ADAMS虚拟样机动态仿真
为了验证双偏心卵形齿轮行星系较已有的椭圆齿轮行星系更适合用在高速水稻插秧机上,这里分别建立了两者的虚拟样机进行了数据分析对比。在 SolidWorks里面对插秧机整体模型进行简化,导入ADAMS,设置材料属性、约束关系、载荷类型并在秧针上建立两个“marker”点(目的是测量秧针运动轨迹)。特别注意要添加接触力[14]来定义齿轮之间的相对运动,不得用齿轮副,这是因为双偏心卵形齿轮啮合时速度是在不断变化的。定义驱动函数为360.0d*time,设置仿真时间“END Time”=“1s”,“Step”=“3600”,并在栽植壁盖与拔叉之间添加一拉压弹簧,预载荷为100N,弹簧刚度系数设为1,阻尼系数默认。应用ADAMS软件的轨迹跟踪和测量功能,精确得到秧针静运动轨迹曲线如图6所示。
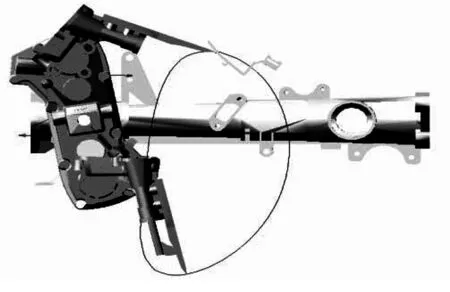
图6 秧针运动轨迹
由图6可见,改装后的运动轨迹满足“腰子形”[15]的要求。
3.3仿真结果分析
合理的运动轨迹是保证插秧机能否顺利作业的前提, 特别是在高速化运转的前提下轨迹显得尤为重要。合理的取秧角应该在12°~30°之间,图7为取秧和插秧时秧针与秧苗、秧台所成角度的关系。这里,取秧角+秧针与秧苗的夹角+秧台倾角≈推秧角+秧针与秧苗夹角 = 90°,故取秧角+秧台倾角≈推秧角。其中,秧台倾角=55°。
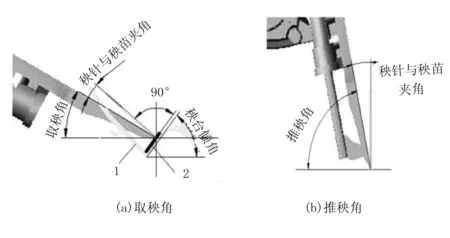
图7 角度关系图
由图7(a)可知:秧针取秧时,秧针与秧苗夹角应尽量小,也就是说取秧角要尽量大,这样可以实现垂直取秧或近似垂直取秧;如果取秧角较小,高速取秧时会将秧苗斜着切下,可能会打断秧苗或伤及其它秧苗。由图7(b)可知:推秧角应该尽量大,否则可能会出现倒秧或插不进秧的情况,实现不了垂直插秧。上述取秧角和推秧角间的关系说明:推秧角和取秧角是一个线性增加的关系,所以在对运动过程进行分析时只需分析取秧角即可。
由于取秧是一个过程,所以取秧角相应地是一个区间,认定秧针尖点分别到秧台1和秧台2距离最近的点作为两个取秧角观测点,测出这段区间插秧角的变化曲线如图8所示。由图8可知:双偏心卵形齿轮行星系下取秧角比椭圆齿轮行星系下取秧角变化范围要大,椭圆齿轮系下取秧角变化范围是11.039°~13.548°,双偏心卵形齿轮系下取秧角变化范围是23.656°~28.928°。显然,双偏心卵形齿轮系在高速取秧过程中更具有优越性,能够保证垂直或近似垂直取秧,在推秧过程中也能改善标准椭圆齿轮行星系分插机构下秧苗容易倒秧和插不进秧的情况,满足农艺要求。由于椭圆齿轮节曲线在设计时变量较少,主要变量是长轴和短轴长度,而双偏心卵形齿轮节曲线在设计时变量不仅有长轴和短轴的长度,而且还有X、Y方向上两个偏心量,更能满足在高速传动时所需的不断变化的传动比。使用双偏心卵形齿轮行星系分插机构能使插秧机在田间作业效果更佳,并在实际耕作中得到了验证。

图8 改装前和改装后取秧角对比图
与此同时,还对改装前后秧针尖点的速度进行了比较,以反映出系统运动的平稳性。秧针速度曲线如图9、图10所示。
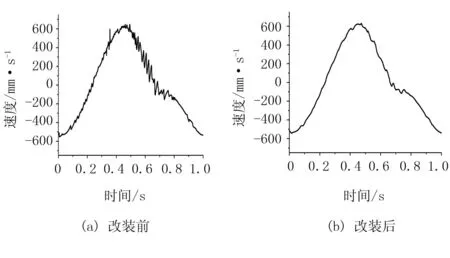
图9 秧针尖点X方向速度

图10 秧针尖点Y方向速度
由图9和图10可以看出:改装后的秧针尖点的速度比较平滑,波动处比改装前的要少很多,因此双偏心卵形齿轮行星系分插机构在稳定性方面也比改装前要优越。
4结论
1)用数学理论并借助于MatLab软件导出了一套符合高速水稻插秧机要求的双偏心卵形齿轮行星系的设计方法,这种方法以标准卵形齿轮节曲线和标准直齿圆柱齿轮渐开线为基础,并结合二分法、辛普生算法、无约束优化法等数值分析方法,为齿轮设计者提供了一种新思路。
2)描述了双偏心卵形齿轮行星系分插机构的机构特点和工作机理。运用动力学仿真软件ADAMS分别对椭圆齿轮系和双偏心卵形齿轮系下的分插机构进行模拟仿真。分析了取秧角和推秧角的关系并且对改装前后取秧角曲线进行对比,结果表明:由于椭圆齿轮行星系在设计上存在局限性,使得秧针在取秧过程中易出现伤秧或在插秧过程中易出现倒秧或插不进秧的情况,而双偏心卵形齿轮行星系则能较好地满足高速下取秧和插秧的要求,可提高工作效率。
3)对改装前后秧针尖点的速度曲线进行分析,结果表明:改装后的装置运动比较平稳,进一步验证双偏心卵形齿轮行星系分插机构的合理性,对高速水稻插秧机的设计提供了一种新思路。
参考文献:
[1]陈建能,赵匀.水稻插秧机分插机构的研究进展[J].农业工程学报,2003,19(2):23-26.
[2]俞高红,谢仁华,赵匀.椭圆齿轮传动后插旋转式分插机构运动分析与试验[J].农业机械学报,2008,39(5):45-48.
[3]李革,李辉,方明辉,等.旋转式分插机构非圆齿轮参数反求法求解[J].农业机械学报,2011,42(8):46-49.
[4]蒋恩臣,彭涛,赵匀,等.变性椭圆齿轮分插机构的运动特性研究[J].东北农业大学学报,2013,44(8):110-114.
[5]陶冶,袁永超.插秧机非圆齿轮行星系分插机构的虚拟制造与仿真[J].研究探索,2012,30(6):45-48.
[6]许纪倩,周娜.非圆齿轮行星轮系分插机构运动分析[J].农业机械学报,2007,38(12):74-77.
[7]代丽,孙良,赵雄,等.基于运动学目标函数的插秧机分插机构的参数优化[J].农业工程学报,2014,30(3):35-42.
[8]吴序堂,王贵海.非圆齿轮及非匀速比传动[M].北京:机械工业出版社,1997:8-45.
[9]肖筱南,赵来军.现代数值计算方法[M].北京:北京大学出版社, 2003:89-94.
[10]李林, 金先级.数值计算方法(MATLAB语言版)[M].广州:中山大学出版社, 2006:64-74.
[11]赵森.中型拖拉机变速箱优化设计平台[D].镇江:江苏大学,2014.
[12]胡仁喜, 马征飞.Solidworks2012中文版机械设计从入门到精通[M]. 北京:机械工业出版社, 2012:199-201.
[13]赵匀,赵雄,张玮炜,等.水稻插秧机现代设计理论与方法[J].农业机械学报,2011,42(3):65-68.
[14]ADAMS实例教程[M].北京:北京理工大学出版社,2002:119-134.
[15]李革.高速水稻插秧机关键技术研究[D].杭州:浙江大学,2006.
Analysis and Research For the Double Eccentric Oval-gear System Transplanting Mechanism
Tan Meilan1a, Zhou Tao1a, Shen Yan2, Hua Xijun1b
(1.Jiangsu University, a.Department of Mechanics & Engineering Science; b.School of Mechanical Engineering, Zhenjiang 212013, China;2.Changzhou Engineering Research Institute of Jiangsu University, Changzhou 213164, China)
Abstract:Rice seeding may be hurt during being taken,and may be upside-down or may not be easily inserted into the soil during being transplanted, which often occur in high-speed rice transplanters equipped standard elliptical-gear planetary system transplanting mechanism. In view of this situation, transplanting mechanism with the double eccentric oval-gear planetary system equipped in high-speed rice transplanters is studied by means of computer-aided software. Based on the standard oval-gear pitch curves and standard cylinder gear involutes, the parameters of double eccentric oval-gears planetary with functional-free pitch curve are analyzed.The solid model of the double eccentric oval-gear planetary system is established. In order to assemble it with other parts of the rice transplanter, its virtual manufacturing structure at rotary transplanting mechanism is given. The modified virtual prototyping of transplanting mechanism is simulated and compared with the existing standard elliptical-gear planetary transplanting mechanism in the performance of the rice transplanter.The results show that the developed new model meets better the requirements of planting trajectory in high speed condition, for the double eccentric oval-gear planetary system has more design variables,more flexible in structure optimization and good stability.
Key words:high-speed rice transplanter; double eccentric oval-gear splanetary system; transplanting mechanism; virtual manufacturing
文章编号:1003-188X(2016)04-0017-06
中图分类号:S223.91
文献标识码:A
作者简介:谈梅兰(1959-),女,江苏溧阳人,教授,博士,(E-mail)tanmeilan@gmail.com。通讯作者:周涛(1989-),男,河南新乡人,硕士,(E-mail)15751011674@163.com。
基金项目:国家自然科学基金项目(51375211)
收稿日期:2015-03-25

