单调有界定理在求递推数列极限的应用

张留伟

（中山大学中法核工程与技术学院，广东 珠海 519082）

单调有界定理在求递推数列极限的应用

张留伟

（中山大学中法核工程与技术学院，广东 珠海 519082）

通过几个具体例子，探讨了利用单调有界定理研究高等数学中递推数列的一般方法.

数列；极限；单调有界定理

数列收敛性问题是高等数学研究的基本问题之一，而利用递推关系定义的数列又是最常见的定义数列的方式.研究递推数列的极限一直是各类考试和练习的热点之一［1-3］.本文将首先研究此类数列的一般性质，利用几何直观性，通过几个易于理解的具体的例子，来说明研究的一般方法.

我们称形如an+1=f（an）的数列为递推数列，其中f是定义在I上并取值于I的函数，I是实数集的一个闭区间，a0是事先给定的I中的实数.通常，我们先研究数列（an）的单调性.

如果函数f在I上单调递增，注意到：

以及

我们知道an+1-an的符号(正或负)与a1-a0的符号相同.因此，数列（an）的单调性与a0和a2的位置关系有关.

如果函数f在I上单调递减，此时，复合函数f莓f在上I单调递增.注意到

我们知道（an）的两个子列（a2n）和（a2n+1）是单调的，并且其单调性互反.

设函数f在I上还是连续的.如果（an）收敛到l，由I是闭区间，我们知道l∈I.对an+1=f（an）两边取极限，由f的连续性，有f（l）=l.我们要解关于未知量l∈I的方程f（l）=l来判断数列（an）可能的极限值.通常，我们称满足f（x）=x的x为函数f的不动点.

接下来，我们通过几个例子来说明求此类极限的一般方法.例1

首先，运用数学归纳法，我们可以证明：

其次，注意到：

因此，数列（an）单调递减.我们得到数列（an）单调递减并且有下界零，由单调有界定理［4］51，（an）收敛.

设

则

解得

从而，我们得到

进一步，我们可以确定数列（an）以何种速度趋向于零，要借助以下引理及其推论：

引理［4］37设limn→∞xn=l，则

由此引理，容易得到如下推论：

推论设limn→∞（xn+1-xn）=l，则

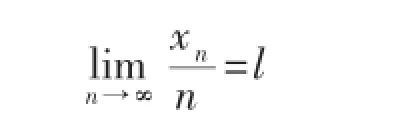
令

则

因此

由推论，得

即

所以

例2

首先，不难看出：

其次，令

通过解方程我们发现f在[0，+∞）上仅有两个不动点：3和5.注意到f在[0，+∞）单调递增，计算得

由f单调递增，（an）n≥1的单调性依赖于a1-a0的符号.注意到：

a1-a0的符号依赖a0与3和5的位置关系.我们分以下情形讨论：

情形1：a0∈[0，3]

此时，a1≥a0.不难看出：坌n∈N，an+1≥an并且an∈[0，3]，即（an）单调递增且有上界3，因此，设其收敛到l，则l∈[0，3].我们已经知道l∈[3，5]，从而l=3.

情形2：a0∈[3，5]

类似地，我们可以得到（an）单调递减且有下界3.设其收敛到l，则l∈[3，a0]奂[3，5）.已知l∈{3，5]，从而l=3.

情形3：a0=5

此时，（an）是常数列5，故收敛到5.

情形4：a0∈（5，+∞）

此时，（an）单调递增，如果其收敛到l，则l≥a0>5，这与l∈{3，5]矛盾.因此，（an）发散，即limn→∞an=+∞.

通常，我们称3为f的吸引型不动点，5为f的扩散型不动点，如图1所示：

例3

令

运用数学归纳法，我们可以证明：

注意到：1+c>1，因此，

注本例中之所以没有分析数列的单调性和有界性，是因为在附近函数的导数的绝对值是小于1的，其是压缩的［3］.

例4

首先，容易看出：

令

我们有

因此，如果数列（an）收敛，其极限必是1.注意到f在[0，∞）上可导，并且

由于f'（1）=-1，我们不能用类似上例压缩的方法确定极限.

我们将证明

由f在[0，+∞）上单调递减，则g=f莓f单调递增.注意到

我们分以下两种情形讨论：情形1:a0∈[0，1]

则

因此，

从而，（a2n）单调递增，（a2n+1）单调递减.此外，

因此，（a2n）和（a2n+1）均收敛.设

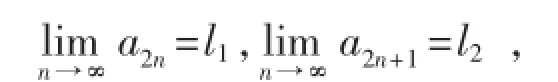
由g是连续的，并且

因此，l1=l2=1，进而

情形2:a0=∈[1，+∞）

类似情形1的方法，我们也可以得到limn→∞an=1.

上述结论如图2所示：

例5设0

由数列（an），（bn）的构造，我们可以用数学归纳法证明：

图2

因此，数列（an）单调递增有上界b0，数列（bn）单调递减有下界a0.从而，它们均收敛.设

从而

以及

由数学归纳法，我们可以证明：n≥1，

即n≥1，

注意到

因此

由

得

［1］吴秉会，魏连锁.压缩映像原理在递推数列极限中的应用［J］.高师理科学刊,2007,27(2):19-21.

［2］徐立峰.递推数列极限的证明与计算［J］.高等数学研究,2011,14(5):51-53.

［3］郑华盛.非线性递推数列极限的不动点解法［J］.高等数学研究,2012,15(5):1-3.

［4］陈纪修，於崇华，金路.数学分析上册［M］.北京:高等教育出版社,2000.

［责任编辑：卓影］

App lication of the M onotone Bounded Theorem to the Lim it of Recurrent Sequences

ZHANG Liu-wei
(Sino-French Institute of Nuclear Engineering and Technology,Sun Yat-Sen University,Zhuhai519082,China)

In this paper,the general methods to determine the limit of recurrent sequences were studied. particularly,the application of the monotone bounded theorem.Some concrete examples to illustrate the method were given.

sequences;limits;monotone bounded theorem

O 174.1

B

1672-402X（2016）02-0001-04

10.13408/j.cnki.gjsxb.2016.02.001

2015-12-05

国家自然科学基金(11271379)

张留伟(1982-)，男，河南沈丘人，中山大学讲师，博士.研究方向：泛函微分方程理论.