延迟LMS(DLMS)自适应滤波器的FPGA设计与实现
柴万东,张立萍,张 迪(赤峰学院 物理与电子信息工程系,内蒙古 赤峰 024000)
延迟LMS(DLMS)自适应滤波器的FPGA设计与实现
柴万东,张立萍,张迪
(赤峰学院物理与电子信息工程系,内蒙古赤峰024000)
摘要:自适应技术已经被广泛应用于数字通信和工业控制等领域.本文利用基于System Generator系统建模的方法,设计了4阶延迟LMS(最小均方误差算法)(DLMS)自适应滤波器系统模型.实验结果表明,利用System Generator系统建模的方法设计自适应滤波器,使得设计效率和滤波器运算速度都大大提高,而且在系统中采用流水线技术可以缩短系统的关键路径,提高系统工作频率.本文在FPGA芯片上最终实现了所设计的自适应滤波器,进行了硬件验证.
关键词:自适应滤波器;SLMS;DLMS;流水线技术;FPGA
1 SLMS结构在实现时存在的问题
自适应滤波器的算法有RTL(递归最小二乘法)和LMS(最小均方算法)等[1],而四阶SLMS算法的方框图表示如图1所示,其输入信号为X(k)=[x (k),x(k-1),x(k-2),x(k-3)]T
权系数为:W(k)=[w0(k),w1(k),w2(k),w3(k)]T
实际输出为:
y=(k)WT(k)X(k) =w0(k)x(k)+w1(k)x(k-1)+w2(k)x(k-2)+w3(k)x(k-3)
权系数递推公式为:W(k+1)=W(k)+μX(k)e(k),
误差信号e(k)为:e(k)=d(k)-y(k)=d(k)-WT(k)X(k)
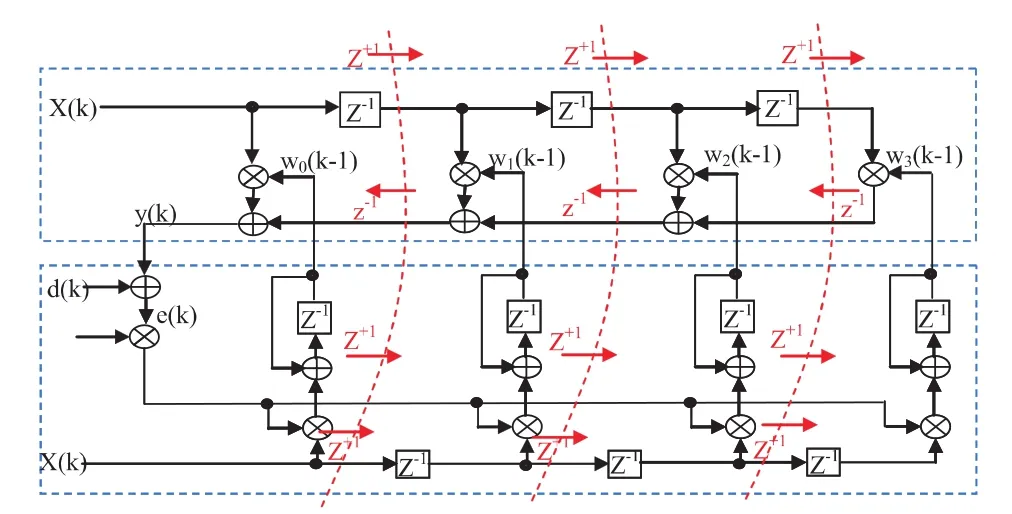
图1 SLMS算法方框图表示
由于采样信号是按串行方式处理的,因此这种结构被称为标准串行LMS(SLMS).加法器链的进位迟延会影响系统可能达到的最高运行速度.如何提高速度以满足信号处理的高效性、实时性一直是人们研究的热点[2].
LMS算法的运算速度受到计算滤波输出和更新滤波系数所花时间的限制.新的采样只有等到这些操作被执行完毕以后才能处理.对于只有一个系数的SLMS,其方框图如图2所示.假定乘法器的传递时间为TM秒,加法器的传递时间为TA秒.考虑反馈环中所有的元素,一旦接收到一个新的采样x (k),计算输出y (k)并更新系数的最短时间为3TM+2TA秒,使用该结构意味着采样周期有一个下界,即最小采样周期为:TS≥3TM+2TA
如果反馈路径中具有延迟单元,将导致更高的采样频率.解决的办法是使用流水线结构.流水线结构是通过改变原始结构以便允许处理一个以上的采样.下面推导具有流水线结构的LMS[3].将具有流水线结构的SLMS称为PIPLMS,其流图如图3所示.注意到反馈环中引入了一个延迟,如果将前一个例子中的传播延迟考虑进来,那么可以得到下列结果.当接收到一个新的采样x(k),将采取下列操作:
路径1中的运算产生μe(k):这需要2TM+TA秒
路径2中的运算生成w0(k-1)+μe(k-1)x(k-1):这需要TM+TA秒
注意,路径2中的运算不需要等到路径1的运算执行完毕,而是一接到输入采样x(k),路径2中的运算就可以执行,这是由于反馈路径中存在的延迟.所以,最小采样周期TS取决于执行路径1或2中的操作所需的最大时间.在这种情况下,路径1中的操作限制了最小采样时间(路径2中的操作需要更短的时间),其值为:
TS≥2TM+T
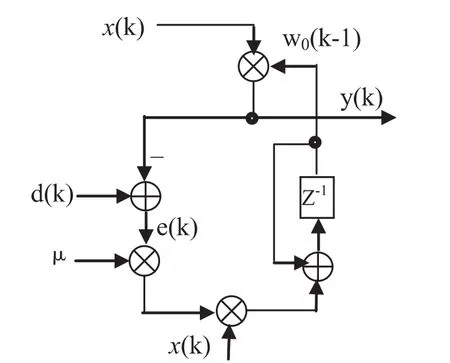
图2 一个系数的SLMS自适应滤波器

图3 PIPLMS(具有流水线结构的SLMS)
这意味着DLMS架构比SLMS架构执行得快.下面说明如何获得流水线型LMS滤波器结构.
2 松弛的前瞻技术
前瞻技术允许将串行LMS(SLMS)结构转换为等价的流水线结构.现在考虑仅有的一个系数的更新:w(k)=w(k-1)+μe(k-1)x(k-1)
由于:w(k-1)=w(k-2)+μe(k-2)x(k-2),
w(k-2)=2(k-3)+μe(k-3)(k-3),
带入到系数更新等式中,得:
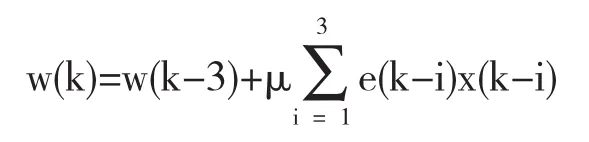
从而可以推导出任意数值的采样“前瞻量”的通用公式.假设前瞻D2个采样的系数更新的通用方程是:

类似地,对于一组系数:
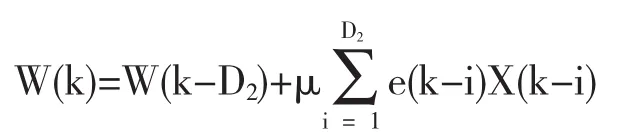
其中,D2是权重更新环路中延时的个数.由于已经有了所需要的信息,系数可以提前D2个采样得到更新.这种变换在权重更新环路中产生D2个锁存器,它们可以通过时序变换对加法操作实现所需要的流水线.但是为了精确的应用前瞻(超前)技术,e(k-i)需要表示成W(k-D2)的函数,总共有D2项e(k-1),e(k-2),…,e(k-D2)需要计算.这将导致所得到的方程很复杂进而大大增加硬件负担.这种开销可以通过引入松弛的前瞻(弛豫超前变换)来降低.
这里要考虑两种简化(松弛)方法:延迟松弛和求和松弛
2.1延迟松弛
延迟松弛假定了e(k)x(k)项在D1个采样期间是缓慢变化的,即假设:
e(k)X(k)≈e(k-D1)X(k-D1)
延迟松弛在误差反馈环路(EFR)中引入D1个延时,则原来的前瞻系数更新方程变为:延迟松弛
延迟松弛通过增加一个额外的、具有D1个采样的延迟单元减少了与w(k-i-1)相关的项的数目.
2.2求和松弛
假设e(k)x(k)项是缓慢变化的,求和松弛是为了降低对求和硬件的需求,采用如下的近似求和使求和项的数目减少.

当LA≤D2时,求和项的数目将减少.D2/LA项的存在是为了保证平均的输出轮廓不变.
注意当应用这些松弛方法时,假设e(k)x(k)是缓慢变化的,即对于平稳的或缓慢变化的环境是合理的,尽管LMS算法被修正,但平均输出轮廓仍保持不变.因此所示架构的瞬时收敛特性将不同于原来的算法,它的有效性需要在特定的应用中进行检验.
使用延迟与求和松弛,得到下列修正后的算法,即松弛的前瞻:(1)
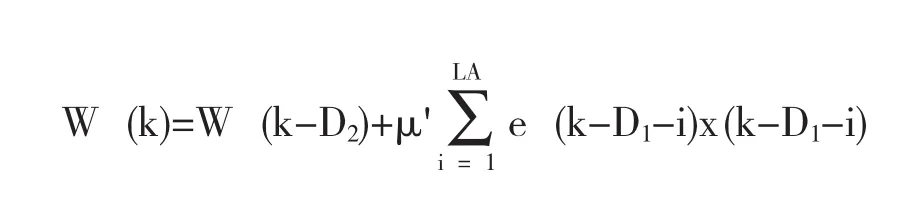
注意μ'包括了求和松弛修正因子,并且1≤LA≤D2.现在误差信号可被表示为
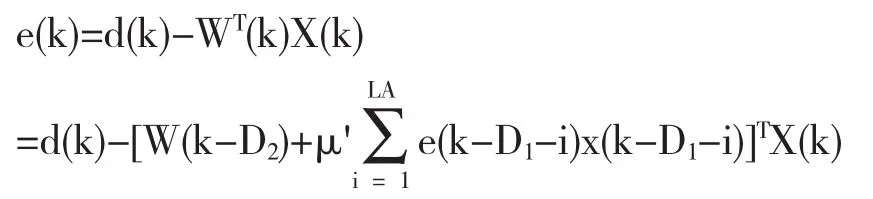
假设μ'足够小,则误差信号可被表示为:


图4 4阶流水线LMS(PIPLMS)自适应滤波器方框图
松弛的前瞻修正算法产生了流水线型LMS (PIPLMS)架构[4].公式(1)和公式(2)完整的描述了流水线LMS滤波器,它的硬件开销是N(LA-1)个加法器,其中N是滤波器系数的个数.PIPLMS架构的方框图如图4所示.
注意,前面提出的与PIPLMS架构相关的算法并非是标准的LMS算法,因此它将具有不同的收敛特性.由于对PIPLMS的全面分析是极其复杂的.故只能针对特定的情况对实现参数LA、D1和D2的某些值做深入细致地研究.然而,在通常情况下,PIPLMS比SLMS收敛得更慢.下面将介绍一种流水线结构及其FPGA实现.
3 延迟LMS(DLMS)自适应滤波器的系统建模与仿真
3.1DLMS算法的方框图
DLMS自适应滤波器是PIPLMS滤波器的一个特例.也就是说当LA=1,D2=1时,PIPLMS滤波器等价于DLMS滤波器.因此DLMS自适应滤波器可以用公式(3)来描述,其方框图表示如图5所示.
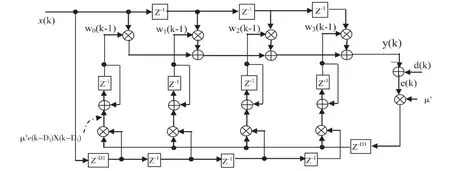
图5 4阶DLMS自适应滤波器方框图
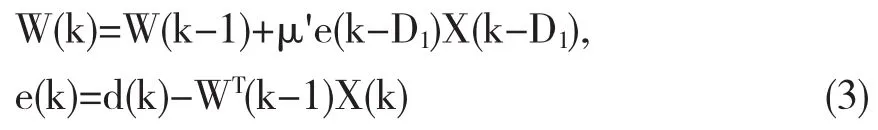
3.2DLMS算法与LMS算法速度[5]比较

图6 LMS算法与DLMS算法收敛性比较
由公式(3)来理解DLMS滤波算法所表达的意义,即通过D1个时刻以前的误差输出信号和D1个时刻以前的输入信号来估计当前的期望信号.相对地,由LMS滤波算法公式可以理解为用当前的误差信号和当前的输入信号来估计当前的期望信号.从时间相关性的角度来看,LMS滤波算法的性能将优于DLMS滤波算法的性能.由图6我们也可以看出DLMS算法的收敛速度较传统的LMS算法要慢一些,但是二者的稳态特性是一致的.考虑到DLMS算法允许硬件拥有高度并行的处理结构,在收敛速度上的代价依然是值得的.
3.3DLMS架构的模型设计和系统仿真[6]
在Matlab/Simu1ink平台上,调用Simu1ink中的IP模块,得到了图7所示的4阶延迟LMS (DLMS)自适应滤波器的模型图.

图7 4阶DLMS自适应滤波器模块图
在图中FIR Filter模块与SLMS模型中的FIR Filter模块相同,而权重更新模块如图8所示.

图8 权重更新模块
它是由延迟模块Delay4~Delay12、加法模块Add4~Add7、乘法模块Mult4~Mult7和移位模块shift组成;为节省硬件资源,取μ=1/1024,就可以将μe(k)运算转化为将e(k)向右移位10位,对应的是模型中的移位模块shift,然后将μe(k)经Delay12延迟后反馈给乘法器模块(Mult4~Mult7),作为乘法器的一个输入,再与对应的x(k-2)相乘,实现权系数的更新.
图9是经过模拟仿真后得到的4阶DLMS自适应滤波器的仿真结果.示波器的第一个通道是期望信号d(k),第二个通道是带有噪声的输入信号x (k),第三个通道是滤波器的输出信号y(k),第四个通道是输出误差信号e(k),从图中可以看出,误差信号e(k)和x(k)中叠加的随机噪声成分很接近,这与理论分析相同,可见自适应滤波器的输出还是比较理想的.
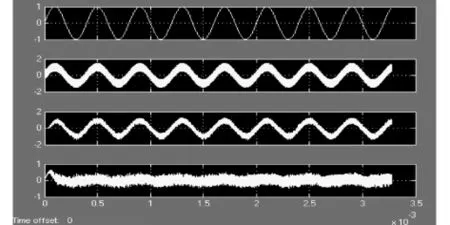
图9 4阶DLMS自适应滤波器的仿真波形图
3.4联合仿真与结果分析
4阶模型通过以后,运行System Generator将模型转化为VHDL语言,并获得相应的ISE工程文件DLMS_cw.ise,采用ModelSim对生成的RTL级VHDL代码进行验证,图10是4阶DLMS自适应滤波器RTL级仿真波形图.
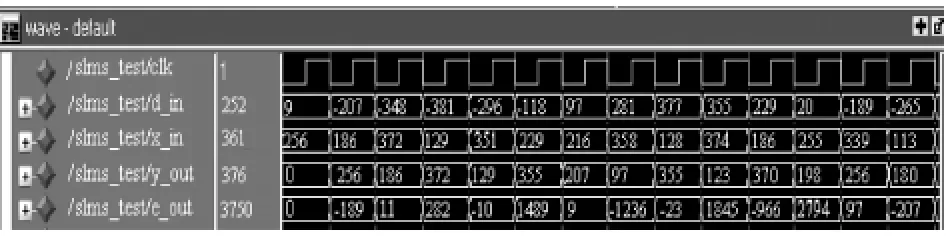
图10 4阶DLMS自适应滤波器RTL仿真波形图
3.5硬件协同仿真
将上述4阶DLMS模块图保存为DLMS.mdl,利用System Generator可以生成一个新的编译模块,复制此模块到设计中并连接好输入输出信号,如图11所示.
将Vitex-4 ML402电路板连接到电脑上,接通电源以后双击硬件协同仿真模块即可进行硬件协同仿真了,硬件仿真波形如图12所示.从图中可以观察到,硬件协同仿真结果与Simulink中的仿真相似.
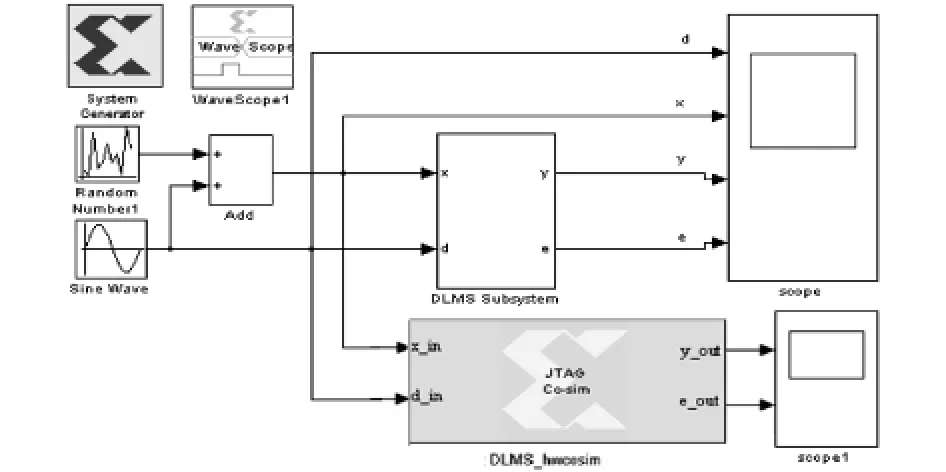
图11 4阶DLMS自适应滤波器的硬件协同仿真模块图
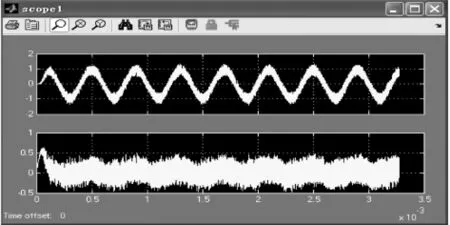
图12 4阶DLMS自适应滤波器的硬件协同仿真波形图
4 结论
通过DLMS与SLMS进行对比,结果表明,在系统中采用流水线技术可以缩短系统的关键路径,系统最高工作频率可以达到58.118MHz,而占用的资源只是略为增加.这是DLMS以牺牲部分收敛速度为代价,获得的高速并行处理能力.
参考文献:
〔1〕沈福民.自适应信号处理[M].西安:西安电子科技大学出版社,2001.11-46.
〔2〕黄埔堪,陈建文,楼生强.现代数字信号处理[M].北京:电子工业出版社,2003.71-88.
〔3〕付文武,周依林.基于高速流水线乘加器的FIR滤波器设计[J].电子设计应用,2003(9):18-21.
〔4〕齐海兵,梅开乡.基于FPGA的流水线LMS自适应滤波器设计[J].微计算机信息,2007,23(6-2):223-224.
〔5〕John G.Proakis,Dimitris G.Manolakis.现代数字信号处理[M].北京:电子工业出版社,2007.702.
〔6〕刘雄飞,高金定,齐海兵.LMS自适应滤波器FPGA实现的新方法[J].压电与声光,2007,29 (1):87-89.
基金项目:量子点中电子自旋量子比特的声子效应研究(11264001)基金项目:国家自然科学基金资助项目
收稿日期:2015年11月5日
中图分类号:TN713-34
文献标识码:A
文章编号:1673-260X(2016)01-0001-04

