He-变分方法在求解广义（2+1）-Boussinesq方程和（2+1）-KP方程中的应用

白　秀，杨培凤（.呼和浩特民族学院　数学系，内蒙古　呼和浩特　0005) （.内蒙古建筑职业技术学院　公共教学部，内蒙古　呼和浩特　00070)



He-变分方法在求解广义（2+1）-Boussinesq方程和（2+1）-KP方程中的应用

白秀1，杨培凤2
（1.呼和浩特民族学院数学系，内蒙古呼和浩特010051) （2.内蒙古建筑职业技术学院公共教学部，内蒙古呼和浩特010070)

摘要：利用He--变分方法构造广义(2+1)-Boussinesq方程和（2+1）-KP方程等的孤子解.该方法也可以适用于求解其它非线性偏微分方程的精确解中.

关键词:偏微分方程；孤子解；He--变分方法；半逆解法

随着非线性科学的迅速发展，非线性微分方程渗透到应用数学、物理学、力学、地球科学、经济学、生命科学和工程技术科学的诸多领域中，从而求解其解析解和数值解是揭示其各类属性方面具有重要的理论意义和实际意义.近三十多来，国内外专家学者在求解非线性偏微分方程的精确解方面做了很多卓有成效的工作，推出很多有效的求解技巧和方法，如齐次平衡法[1]-[3]、辅助方程法[4,5]、Paialeve截尾展开法[6]、Tanh函数方法[7]、Exp—展开法[8]、变分迭代法[9]、He-变分方法[10,11]、同伦摄动方法[12]和广义（G'/G）-展开法[13]等．这些方法中，He-变分方法具有既简单又直接的特性，它基于He—半逆解法[10]建立一种巧妙的变分泛函，进而构造非线性偏微分方程（组）的孤立子解等精确解.该方法已成功应用到求解Benjanmin One方程[14]和吸孤子方程[15]的孤子解中.

本文从文献[11,14-16]得到启示，利用变分方法对广义（2+1）—Boussinesq方程和（2+1）—KP方程等进行求解，成功推出这些方程的孤子解.

1　利用变分法求解广义(2+1)—Boussinesq方程

著名的广义(2+1)—Boussinesq方程[17]为

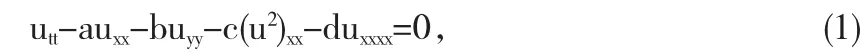
其中参数a,b,c和d是任意常数,且cd≠0，此方程在浅水波长波分析和表层多孔渗水物质材料的水渗透分析中广泛应用.

根据变分方法的基本思想，设行波变换u(x,y,t)=u(ξ),且ξ=kx+ly-λt，对方程（1）行波约化，再将所得到的低维形式常微分方程经两次积分得到下列二阶微分方程：

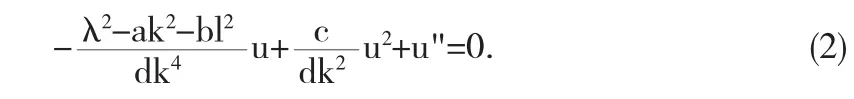
再利用半逆解法，便得（2）的如下变分公式

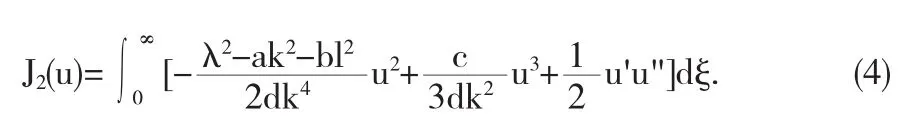
设方程（2）的孤子解为

其中ξ=kx+ly-λt.

再把（5）带入到（3）里，得到下列双参数函数

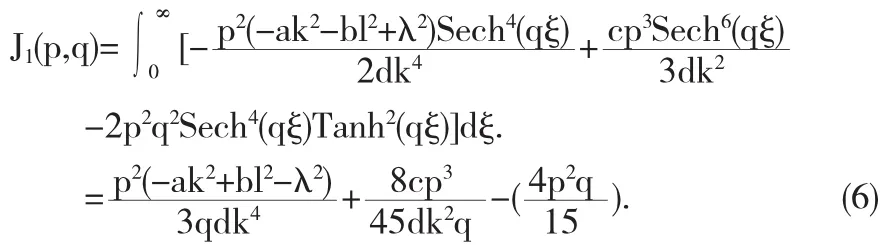
同样，也可以将（5）带入到(4)得到对应的双参数函数J2(p,q).

为了讨论（6）的稳定性，求得：

然后，建立如下方程组：

求解上述方程组，得到

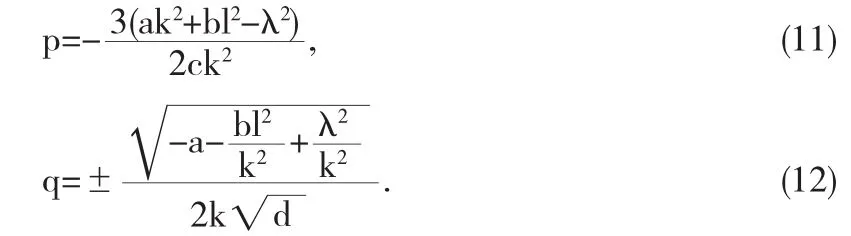
所以,广义(2+1)—Boussinesq方程（2）的孤子解为：

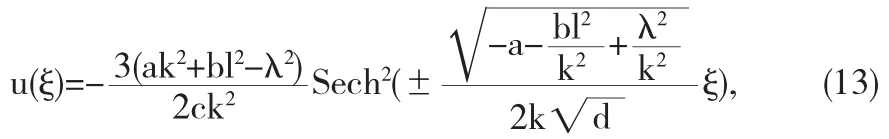
其中ξ=kx+ly-λt.

2　利用变分方法求解（2+1）—KP方程

具有两个空间变量与一个时间变量的(2+1)—KP方程[18]

其中α为任意常数，该方程描述弱色散和非线性介质微扰现象.

设行波变换u(x,y,t)=u(ξ),且令ξ=kx+ly-λt，对方程（14）行波约化，再将所得到的低维形式常微分方程经两次积分得到下列二阶微分方程：

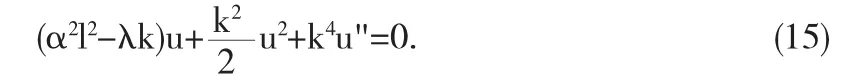
再利用半逆解法，可得到（15）的变分公式

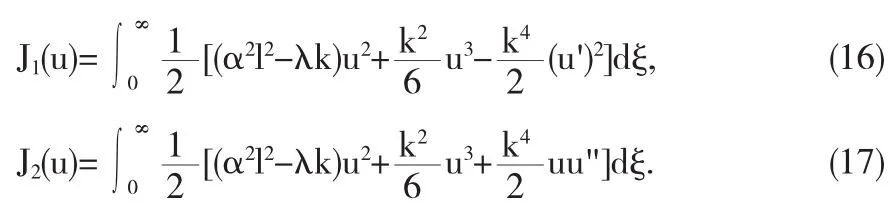
为了求解该方程，通过构造下列2种形式的孤子解，能得到方程（14）的解：

情形1设(14)的孤子解为

其中ξ=kx+ly-λt.

把（18）带入到（16）里，得到双参数函数

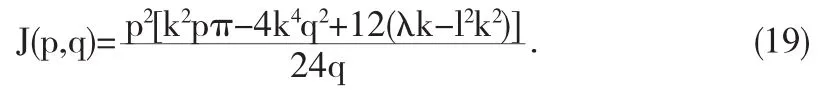
同样，可以带入（17）里得到对应的双参数函数J(p,q).

为了考虑(19)的稳定性,求得：

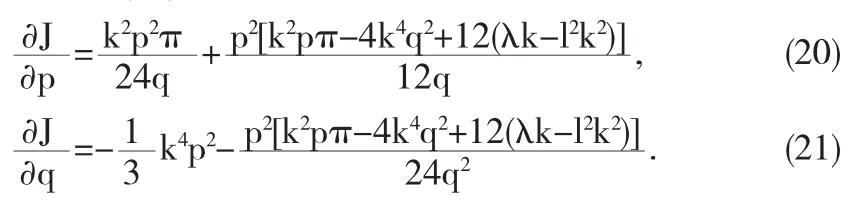
再建立联立方程组(20)和(21)，并求解得到：

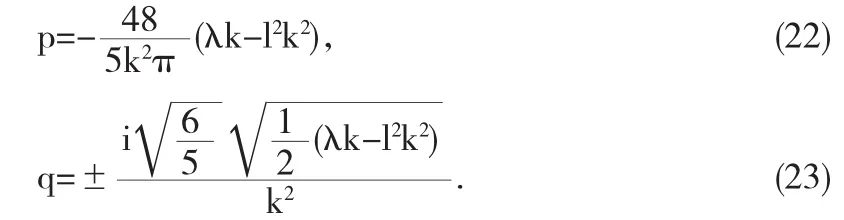
所以，原(2+1)维KP方程（14）的孤子解为：

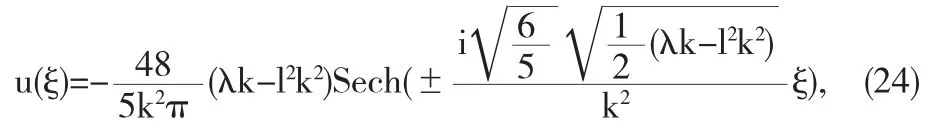
其中ξ=kx+ly-λt.

情形2设(14)的孤子解为

其中ξ=kx+ly-λt.

把（25）带入到（16）里，再对通过讨论得到的双参数函数的稳定性，求关于参数p，q的方程组，并求解得到参数p，q以下解：

所以，原(2+1)维KP方程（14）又具有以下形式的孤子解：

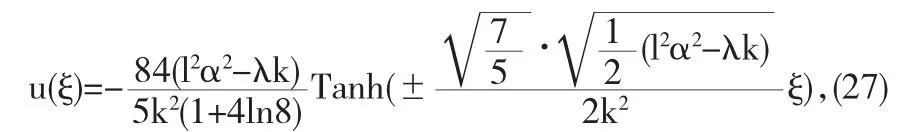
其中ξ=kx+ly-λt.

3　结论

He--变分方法是求解偏微分方程精确解的有效工具，本文基于He—半逆解法，对广义(2+1)—Boussinesq方程和（2+1）—KP方程等进行构造对应变分公式，进而寻找这些方程的孤子解.这些结果显示，该变分方法简单明了，利用它可以构造其它诸多非线性偏微分方程的孤立子解和周期解.

参考文献：

〔1〕M.L. Wang. Solitary solutions for variant Boussinesq equations[J].Phys Lett A, 1995(199): 169 - 172.

〔2〕M.L. Wang. Exact solution for a compound KdV -Burgers equation[J],Phys Lett ,1996(213): 279 - 287.

〔3〕M.L. Wang. Application of a homogeneous balance methods to exact solutions of nonlinear equations in Mathematical physics[J]. Phys Lett A, 1996(216): 267-270.

〔4〕李志斌.非线性数学物理方程的行波解[M].北京：科学出版社，2006.

〔5〕Sirendaoreji, Sun J. Auxiliary equation method for solving nonlinear partial differential equati- ons [J]. Phys Lett A, 2003(309): 387-396.

〔6〕李翊神.孤子与可积系统[M].上海：上海科技教育出版社，1999.

〔7〕E.G. Fan. Extended tanh-function method and its applications to nonlinear equations [J]. Phys Lett A, 2000 (277): 212-218.

〔8〕J.H. He, X.H. Wu. Exp-function method for nonlinear wave equations [J], Chaos Solition Fractals, 2006(30): 700-708.

〔9〕J.H. He. Variational iteration method-Some recent results and new interpretations [J], Journal of Computational and Applied Mathematics, 2007 (207):3-17.

〔10〕J.H. He. Some Asymptotic Methods for Strongly Nonlinear wave equition [J], Internat J. Modern Phys. B, 2006 (20) (10):1141-1199.

〔11〕J.H. He. Non-perturbative methods for strongly Nonlinear problems [J] , Berlin: dissertation. de-Verlag im Internet GmbH, 2006.

〔12〕J.H. He. New interpretation of homotopy perturbation method[J], Internet J. Modern Phys. B, 2006 (20): 2561-2568.

〔13〕Erdunbuhe, Temuerchaolu. A Generalized (G'/G) -Expansion Method and Its Applications to the Whitham-Broer-Kaup-Like Equations [J].内蒙古师范大学学报（自然科学汉文版）, 2012，(41)(2):120-131.

〔14〕Z.L. Tao. Variational approach to the Benjamin Ono equation [J]. Nonlinear analysis: real world applications, 2009 (10):1939-1941.

〔15〕Z.L. Tao. Solving breaking solution equation by He’s variational method [J] . Comput. Math. Appl., 2009 (58):2395-2397.

〔16〕J. Zhang, Variational approach to solitary wave solution of the generalized Zakharov equation [J], Comput. Math. Appl., 2007 (54):1043–1046.

〔17〕H.T. Chen, H.Q. Zhang. New double periodic and multiple soliton solutions of the eneralized (2+1)-dimensional Boussinesq equation[J]. Chaos Solitons Fract, 2004(20)(4):756-769.

〔18〕Kadomtsev, B.B., Petviashvili, V.I.. On the stability of solitary waves in weakly dispersive media [J], Sov Phys Dokl, 1970 (15) (1):539-541.

基金项目:内蒙古自然科学基金资助项目( 2013MS0118),内蒙古高等学校科学研究资助项目(NJZC13276，NJZZ14210)和呼和浩特民族学院科技创新团队建设资助项目(CXTD1402)

收稿日期：2015年10月22日

中图分类号：0175.29

文献标识码：A

文章编号：1673-260X（2016）01-0010-02