例谈如何从习题教学中培养学生的数学能力

◎陈永胜

例谈如何从习题教学中培养学生的数学能力

◎陈永胜

从实例中总结教学实践，旨在提醒教师重视数学教材中习题教学。从教学实践中总结经验，反思教学方法，促进教学质量的提高。从“几何图形初步”习题实例教学中培养学生对几何图形认知与数学学习兴趣。让学生经历从“模型－－图形－－文字－－符号”的过程中获得几何学习方法。由此较好地培养学生的良好的学习习惯和分析思维意识。

习题教学；能力培养；方法

新人教版七年级数学上册第四章是“几何图形初步”，这一章是初中阶段中“图形与几何”领域的第一章。在几何学习中有启蒙和奠基的作用。教材也旨在通过现实世界中丰富多彩的实物模型抽象出的几何图形激发学生学习几何的兴趣。教材内容也尽量从学生的观察、操作、想象、交流活动中抽象出几何图形性质。让学生经历从“模型——图形——文字——符号”的过程中获得几何学习方法。在这一章的习题中有许多题也体现了学习几何知识方法，主要有以下几个方面来培养学生的数学分析思维能力。

一、培养学生从实物模型抽象几何图形的能力

几何图形本就是从实物图形抽象出来的，教材内容体现了这一点，习题中许多题也如此。典型题有教材121页第2第3题就是让学生从“木马”和“猫”图中找几何图形。题较简单但可培养学生仔细看图和抽象几何图形的能力。在课堂练习教学中只要较好利用这些习题就可培养学生抽象图形的能力。

二、注重学生从动手能力到想象能力的提升

动手操作是学习几何知识的一个基本途径，也是从形象到抽象的能力形成过程。这一点在教材中有许多体现，如圆柱、圆锥、正方体等的展开图，在课题学习中也重点培养。而教材中许多习题也体现着力培养学生的动手操作能力，如123页第12题：你能把一个正方形纸片折叠成一个三棱锥吗？动手试一试。这就要求学生从三棱锥特点去折叠纸张才能找到折叠方法。这样在折纸中培养了学生的动手能力和空间想象能力，而这正是今后学好几何的必备能力。

三、培养学生将几何语言转化为图形的能力

正确理解几何语言是学习几何知识的必备条件之一，也是由“文字－图形－符号”转化中必需具备的能力。这一点在教材习题中也有较好体现，如129页第4题：读下列语句画出图形；直线L经过A、B、C三点，并且C点在A和B之间。两条线段m与n相交于点P，p是直线A外一点，过点P有一条直线与直线a相交于点Q．这一题就较好体现了文字、图形、符号之间互相转化能力的培养。教材中还有许多习题也是检测学生正确理解语言的能力，教师当然要利用这些习题着力培养学生理解几何语言的素养。

四、渗透分类讨论意识，认识几何图形的多样性

分类讨论题是初中数学中常见题型可培养学生全面思考的习惯。在这一章习题中也体现了要培养学生分类讨论的意识，如130页第10题：点A、B、C在同一条直线上，AB＝3cm，BC＝1cm，求AC长。这一题计算简单，只是学生往往只考虑一种情形而丢掉另一种情况。这题也可变为：点A、B、C在同一条直线上，AB＝1cm，BC＝3cm，求AC长。或变难点：点A、B、C在同一条直线上，E、F分别是AB、AC的中点，若AB＝3cm，BC＝1cm，求EF长。由这类习题或变式习题教学中去引导学生对图形多样性的考虑，以此培养学生分类讨论意识。

五、培养学生对几何图形规侓的归纳方法

几何图形的规律性寻找过程往往是从特殊到一般的分析过程。对几何图形规律性探索有助于学生思维的开拓和探究兴趣的培养。教材中130页第12题：两条直线相交有一个交点，三条直线相交最多有几个交点？四条直线呢？你发现了什么规律吗？学生从有限的画图中不难找到这个规律。教师可利用这道题继续探索如直线上有n个点时一共有多少条线段。一块蛋羔切n刀最多可分成多少块等题型，让学生认识几何图形中含有的代数规律。

六、重视几何推理思维逻辑性的培养做到计算有理有据

从这一章教材内容来看并不要求学生会用严格的逻辑推理来写计算过程，但在习题中还是有许多题要求学生在理解概念和性质基础上进行简单说理。如134页第5题：如图1

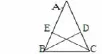
BD和CE分别是∠ABC和∠ACB的平分线，且∠DBC＝∠ECB＝31o，求∠ABC和∠ACB的度数，它们相等吗？这一题就要求学生在理解角平分线基础上进行说理计算。教师可利用这一题的教学来培养学生对几何计算题的说理意识，而不是只有算术计算。

以上只是从“几何图形初步”这一章中的习题教学中培养学生的数学学习能力。修定版的新人教版数学教材和上一版相比除内容略有调整外较大变化就是习题增加和调整。因此教师只要充分利用教材中习题，把这些有代表意义的练习题在课内就完成，通过讲练结合就能较好培养学生的良好解题习惯。我们在教学时总喜欢追求数量众多和新颖的课外题，总担心学生没做过某种题型在考试中就不会解这类题，总想让学生多见识各类题型。其实只要我们潜心研究书中习题以题带面以题变式就能很好地培养学生的学习方法和解题能力。尤其是在启蒙和基础课教学中不要让学生感觉题目难而多，关注课本习题教学就能较好地培养学生的良好的学习习惯和思维意识。

（作者单位：新疆生产建设兵团第二师三十四团35学校 841507）