让“三角形成立的条件”应用的更自然——高一（上）“研究性”公开课教学设计

◎张成鹏

让“三角形成立的条件”应用的更自然
——高一（上）“研究性”公开课教学设计

◎张成鹏

以a，b，c为三边长的线段构成三角形的充要条件是“任意两边之和大于第三边”，还可以自然地转化为“三条线段中最长的小于其他两条线段的和”．本文巧妙的设计了如何将“三角形成立的条件”应用的更自然，如何更好的“转化”为不等式组恒成立及引导学生思考“以函数值f（a），f（b），f（c）为三边长的线段构成三角形的等价转换”．

构成三角形；充要条件；三角形稳定函数

背景分析：笔者执教于上海市华东师范大学第二附属中学，现所带班级为高一理科班、科技创新实验班，“研究性学习”经常在这两个班级的课堂上开展．借与辽宁数学教研员考察我校的机会，开设一节题为《让“三角形成立的条件”应用的更自然》的公开课．选择这个题目的理由是：（1）沪教版教材中高一第二章已经介绍完不等式，第三章函数内容也已经过半；（2）高中“不等式恒成立”的数学思想学生已然接触过；（3）利用不等式恒成立解答函数中的问题接触较少．基于以上几点，选择从众所周知的“以a，b，c为三边长的线段构成三角形的充要条件”出发，一起探究几个经典数学问题．

教学目标：

1．掌握以a，b，c为三边长的线段构成三角形的充要条件；

2．理解以函数值f（a），f（b），f（c）为三边长的线段构成三角形的等价转换；

3．体会“不等式恒成立”的数学思想所体现的数学的“美”．

教学重点与难点：如何巧妙应用“三角形成立的条件”解答数学问题．

教学过程：直接应用、间接应用、等价转化

环节1．回顾与思考以a，b，c为三边长的线段构成三角形的充要条件

（3）若a＝max｛a，b，c｝，则a＜b＋c，即：三条线段中最长的小于其他两条线段的和；

（4）若a＝min｛a，b，c｝，则a＞max｛b－c，c－b｝，即：三条线段中最短的大于其他两条线段的差；

设计意图：（1）引导学生回顾三条线段构成三角形的充要条件；（2）引导学生尝试将构成三角形的条件“转化”为数学语言；（3）引导学生思考构成三角形的其他等价条件．

环节2．“以a，b，c为三边长的线段构成三角形的充要条件”的直接应用

问题1．设集合A＝｛（x，y）｜x，y，1－x－y是三角形的三边长｝，则A所表示的平面区域（不含边界的阴影部分）的面积是？

解：根据任意三角形两边之和大于第三边的性质得：

设计意图：（1）引导学生直接利用“任意两边之和大于第三边”这个性质转化为不等式组“恒成立”问题；（2）引导学生探究不等式组在平面上所表示的区域（线性规划问题）．

a，b，c都可以成为某个三角形三边的长？

所以根据任意三角形两边之和大于第三边的性质得：

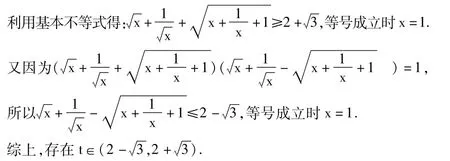
设计意图：（1）引导学生再次直接利用“任意两边之和大于第三边”这个性质转化为不等

式组“恒成立”问题，并巧妙的等价转化为更为简单的两个不等式“恒成立”问题；（2）引

导学生体会“参变量分离”的数学思想在含参变量的不等式恒成立问题中的应用．

环节3．“以a，b，c为三边长的线段构成三角形的充要条件”的间接应用

问题3．已知三个正数a，b，c，对于任何正整数n，都有以an，bn，cn为边长的三角形，证明：这些三角形都是等腰三角形．

证明：（法一）不失一般性，设a≥b≥c．因为对于任何正整数n，都有以an，bn，cn为边长的三角形，所以根据三条线段中最长的小于其他两条线段的和这个性质有an＜bn＋cn，n∈N*．（i）若三个正数a，b，c中有两个相等，则结论成立；

综上，这三个正数a，b，c中必有两个相等，即这些三角形都是等腰三角形．

（法二）不失一般性，设a≥b≥c．因为对于任何正整数n，都有以an，bn，cn为边长的三角形，所以根据三条线段中最长的小于其他两条线段的和这个性质有an＜bn＋cn，n∈N*．而an－bn＝（a－b）（an－1＋an－2b＋…＋bn－1）≥（a－b）·n·cn－1，所以得到（a－b）·n·cn－1＜cn，由a对任何正整数n都成立，可得a＝b，即这些三角形都是等腰三角形．

设计意图：（1）引导学生从“三条线段中最长的小于其他两条线段的和”这个性质出发思考问题；（2）引导学生欣赏数学中的“极限”思想；（3）引导学生体会“对任何正整数n都成立”这一无穷多个条件的含义．

环节4．“以函数值f（a），f（b），f（c）为三边长的线段构成三角形”的等价转换

问题4．一个函数f（x），如果对任意一个三角形，只要它的三边长a，b，c都在f（x）的定义域内，就有f（a），f（b），f（c）也是某个三角形的三边长，则称f（x）为“三角形稳定函数”．

解：（1）设三角形的三边长分别为a，b，c，不妨假设a≤c，b≤c，则a＋b＞c．

对于f2（x），3，3，5可作为一个三角形的三边长，但32＋32＜52，所以f2（x）不是“三角形稳定函数”．

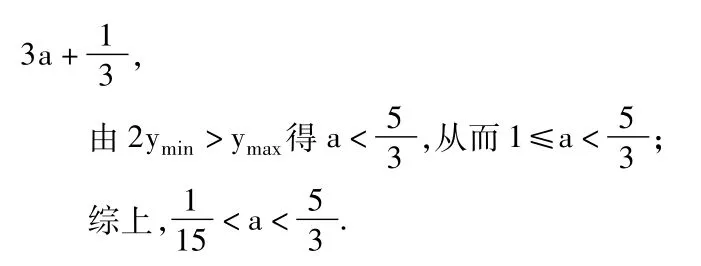
设计意图：（1）引导学生发现并掌握以函数值f（a），f（b），f（c）为三边长的线段构成三角

形要等价转换为2f（x）min＞f（x）max对定义域中的x恒成立问题；（2）带领学生再次体会

含参变量的“对勾函数”在给定区间上的最值问题．

环节5．思考

思考2．已知正数a，b，c满足（a2＋b2＋c2）2＞2（a4＋b4＋c4），证明：以正数a，b，c为边长的线段可构成三角形．［1］

思考3．思考以a，b，c为三边长的线段构成锐角、钝角、直角三角形的充要条件．

［1］计正荣．三条线段构成三角形的充要条件［J］．中等数学，1995．4

［2］黄万尧．用三条线段为边围成三角形的充要条件．数学教学，1982

（作者单位：华东师范大学第二附属中学 201203）