“超级全能生”2016高考全国卷26省联考(甲卷)(本试卷适用于使用全国卷Ⅱ地区)
“超级全能生”2016高考全国卷26省联考(甲卷)(本试卷适用于使用全国卷Ⅱ地区)
(时间:120分钟 满分:150分)
[编者按]本次考试由新东方优能中学、《教学考试》杂志社共同发起组织,全国26个省市的数十万考生参加,试题创新度较高,吻合高考命题趋势,本刊特刊发以供广大读者考前模拟检测,希望对大家备考有所帮助。
一、选择题(本题共12小题,每小题5分,共60分)
1.(理)已知集合B={1},C={3},A∪B={1,2},则( )
C.A∪C={1,2,3}D.A∪C={2,3}
(文)已知集合B={1},A∪B={1,2},则A=( )
C.{1,2}D.{2}或{1,2}
A.-1-2iB.-1+2i
C.1+2iD.1-2i
3.(理)掷一枚均匀的硬币4次,则出现正面的次数多于反
面的次数的概率为( )

(文)掷一枚均匀的硬币4次,则出现“3次正面朝上,1次反面朝上”的概率为( )

4.“xy≠0”是“x≠0”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分又不必要条件
5.一个蜂巢里有1只蜜蜂,第1天它飞出去找回3个伙伴;第2天有4只蜜蜂飞出去各自找回了3个伙伴,…,如果这个找伙伴的过程继续下去,第6天所有的蜜蜂归巢后,蜂巢中一共有________只蜜蜂.( )
A.972B.1 456
C.4 096D.5 460
6.如图是一个空间几何体的三视图,其中正视图与侧视图完全一样,俯视图的外框为正方形,则这个几何体的表面积是( )

A.80-2πB.80
C.80+4πD.80+6π
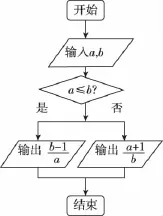

A.y=-tanx
C.y=sin2x+cos2x
D.y=2cos2x-1
A.f(x)=ax+b
B.f(x)=xa
C.f(x)=logax(a>0,a≠1)
D.f(x)=x2+ax+b
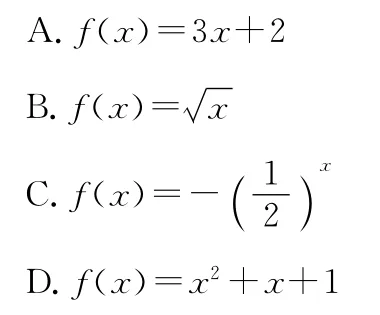



12.以下关于x(x≥0)的不等式ln(x+1)+kx2-x≥0的结论中错误的是( )

二、填空题(本题共4小题,每小题5分,共20分)
13.等腰直角三角形的直角顶点位于原点,另外两个点在抛物线y2=4x上,则这个等腰直角三角形的面积为________.
14.(理)若关于x的不等式-x2+x>mx的解集为{x|-1<x<0},则二项式(1+mx)2016的展开式中x的系数为____________.
(文)若关于x的不等式-x2+x>mx的解集为{x|-1<x<0},且函数f(x)=x(x-m)2在x=n处有极小值,则n=_____________.
15.(理)等比数列{an},an>0,a1=256,S3=448,Tn为数列{an}的前n项乘积,则当Tn取得最大值时,n=_____________.
(文)等比数列{an},an>0,a1=256,S3=448,Tn为数列{an}的前n项乘积,则T17=_____________.
16.(理)已知向量a=(m,n),b=(1,1),满足a·b≥2,且a·(a-2 b)≤0,则a·b的取值范围是____________.
(文)已知向量a=(m,n)(m≥0,n≥0),b=(2,-3),c=(3,-2)满足a·b≥-3,且a·c≤3,则|a|的最大值为____________.
三、解答题(本题共6小题,共70分)
17.(12分)△ABC中,角A,B,C的对边分别为a,b,c,若
2sinB-sinC=2sin(A-C).
“骰子”有6个面,相对面点数的和为7,如果将一摞骰子摆起来,只看到最上面的骰子朝上一面的点数就可以知道这一摞骰子“看不见”的所有面的点数之和(若有a颗骰子,最上面一粒骰子朝上的点数为b,则“看不见”的点数之和为
(1)求cos A;
18.(12分)(理)某超市某种面包进货价为每个4元,实际售价为每个4.5元,若当天不能卖完,就在闭店前以每个3元的价格全部处理.据以往统计日需求量x(单位:个)的情况如下:

日需求量x __(0,400](400,600](600,800](800,1 000]____频率____ ___0.2 0.4 0.3 0.1____
若某日超市面包进货量为600.
(1)若以日需求量x所在区间的中间值为估计值,根据上表列出当日利润y的分布列;
(2)估计超市当日利润y的均值.
(12分)(文)某毕业班统计全班40名学生报名参加学科竞赛和报名参加自主招生的数据如下:(1)从该班随机选1名同学,求该同学仅报名参加其中一项的概率;

报名参加学科竞赛未报名参加学科竞赛_报名参加自主招生6 28________ 2 4________未报名参加自主招生
19.(12分)已知三棱柱ABC—A1B1C1,侧棱AA1垂直于底面ABC,∠ABC=,AB=BC=AA1=4,D为BC的中点.

(1)若E为棱CC1的中点,求证:DE⊥A1C;
(2)(理)若E为棱CC1上异于端点的任意一点,设CE与平面ADE所成角为α,求满足时CE的长.
(2)(文)若E为棱CC1上异于端点的任意一点,当三棱锥C1—ADE的体积为时,求异面直线DE与AC1所成角的余弦值.
(1)求椭圆C的方程;
(1)求函数的单调性;
请考生在第22~24三题中任选一题作答,如果多做,则按所做的第一题计分.
22.(10分)选修4-1:几何证明选讲如图所示,AB为圆O的直径,BC,CD为圆O的切线,B,D为切点.
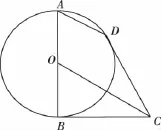
(1)求证:AD∥OC;
(2)若圆O的半径为1,求AD·OC的值.
23.(10分)选修4-4:坐标系与参数方程
已知A,B(不与原点O重合)分别在圆C1:(x-2)2+y2=4与圆C2:(x-1)2+y2=1上,且OA⊥OB.
(1)若以原点为极点,x轴的正半轴为极轴建立极坐标系,当A的极角为时,求A,B的极坐标;
(2)求|OA|·|OB|的最大值.
24.(10分)选修4-4:不等式选讲
如果关于x的不等式|x-3|+|x-4|≤|a|的解集为空集.
(1)求实数a的取值范围;
(2)若实数b与实数a取值范围完全相同,求证:|1-ab|>|a-b|.
参考答案
1.(理)B (文)D
2.A
3.(理)C (文)B
4.A 5.C 6.C 7.C 8.B
9.(理)D (文)D
10.(理)B (文)A
11.D 12.B 13.16
14.(理)4 032 (文)2
15.(理)8或9 (文)1

18.(理)解:(1)若以日需求量x所在区间的中间值为估计值,则其分布列为

当x=200时,y=200×(4,5-4)-(600-200)×1=-300;(3分)
当x=500时,y=500×(4,5-4)-(600-500)×1=150;(4分)
当x=700时,y=600×(4,5-4)=300;(5分)
当x=900时,y=600×(4,5-4)=300.(6分)
所以当日利润y的分布列

(2)Ey=-300×0.2+150×0.4+300×0.4=120(元).(12分)
(文)解:(1)设从该班随机选1名同学,该同学仅报名参加其中一项的事件为A,则.(4分)
(2)设报名参加自主招生的同学中任取2人,恰好1人两项都报名的事件为B,设参加两项的2名同学分别为a,b,仅参加自主招生的4名同学分别为c,d,e,f,(6分)
从报名参加自主招生的同学中任取2人有ab,ac,ad,ae,af,bc,bd,be,bf,cd,ce,cf,de,df,ef,共15种.(8分)
其中恰好1人两项都报名的情况的有ac,ad,ae,af,bc,bd,be,bf,共8种(10分)


解得T(0,1).(10分)
当直线l0的斜率不存在时,易知A(0,1),B(0,-1),则圆的方程为x2+y2=1,
易知过T(0,1)(11分)
综上所述,存在定点T,其坐标为T(0,1).(12分)
21.解:(1)y=f(x)的定义域为{x|x>0},(1分)
令f′(x)>0,x>1,令f′(x)<0,0<x<1,(3分)
所以原函数的单调递增区间为(1,+∞),单调递减区间为(0,1).(4分)
(2)由(1)知y=f(x)的最小值为f(1)=0,(5分)

22.解:(1)连接BD,OD,∵CB,CD是圆O的两条切线,∴BD⊥OC.
∴∠ODB+∠DOC=90°.(1分)
又AB为圆O的直径,∴AD⊥DB,∴∠ADO+∠ODB=90°,(2分)
∴∠DOC=∠ADO,(4分)
∴AD∥OC.(5分)

(2)∵AO=OD,∴∠DAO=∠ADO=∠DOC,(6分)
∴Rt△BAD∽Rt△COD,(8分)
AD·OC=AB·OD=2.(10分)
23.(1)圆C1:(x-2)2+y2=4的极坐标方程为ρ=4cosθ,(1分)
圆C2:(x-1)2+y2=1的极坐标方程为ρ=2cosθ,(2分)

所以y=f(x)的最小值为1,(3分)
所以|a|<1.(5分)
(2)由(1)|a|<1,所以|b|<1,(6分)
因为(1-ab)2-(a-b)2=(1-a2)(1-b2),(8分)
而|a|<1,|b|<1,
所以a2<1,b2<1,(9分)
所以原不等式得证.(10分)

