有限长轴颈轴承的弹性流体动力润滑分析
于如飞, 陈 渭
(西安交通大学现代设计及转子轴承系统教育部重点实验室, 陕西 西安710049)
有限长轴颈轴承的弹性流体动力润滑分析
于如飞, 陈渭
(西安交通大学现代设计及转子轴承系统教育部重点实验室, 陕西 西安710049)
摘要:为研究变形对有限长轴颈轴承弹流润滑特性的影响,利用Winkler弹性基础模型对其进行分析,使用压力和膜厚双重迭代方法进行数值模拟求解。其结果表明:载荷越大,刚性轴承与柔性轴承的油膜压力和厚度差异越大;在轴承表面变形的条件下,随载荷的增大,偏心率随转速增大而减小的幅度变小,偏位角随转速增大而增大的幅度亦变小;随转速的增大,偏心率随载荷增大而增大的幅度变大,偏位角随载荷增大而减小的幅度亦变大。此外,还研究了在定载荷条件下轴承宽度、厚度、润滑油黏度、间隙等参数对油膜压力、厚度及破裂位置的影响规律。该研究成果可为轴颈轴承的设计及其性能计算提供相应的理论参考。
关键词:Winkler模型; 有限长轴颈轴承; 弹流润滑; 偏位角;偏心率
轴颈轴承也被称为径向滑动轴承,作为一种结构简单、连接可靠的共形铰接副,在实际工程中被广泛应用。一般的轴颈轴承由旋转轴、轴套和轴承座组成,根据工况条件及运行环境的不同,通常可分为无油润滑、贫油润滑和流体润滑3种状态,流体润滑又分为流体静压润滑和流体动压润滑。在流体润滑的条件下,轴和轴套被油膜完全隔离开,即包括重力和外载荷在内的全部力均由油膜承受。除了理想状况外,在实际中轴与轴套的中心并不重合,两者之间的距离就是所熟知的偏心距,此处用e表示,如图1所示。
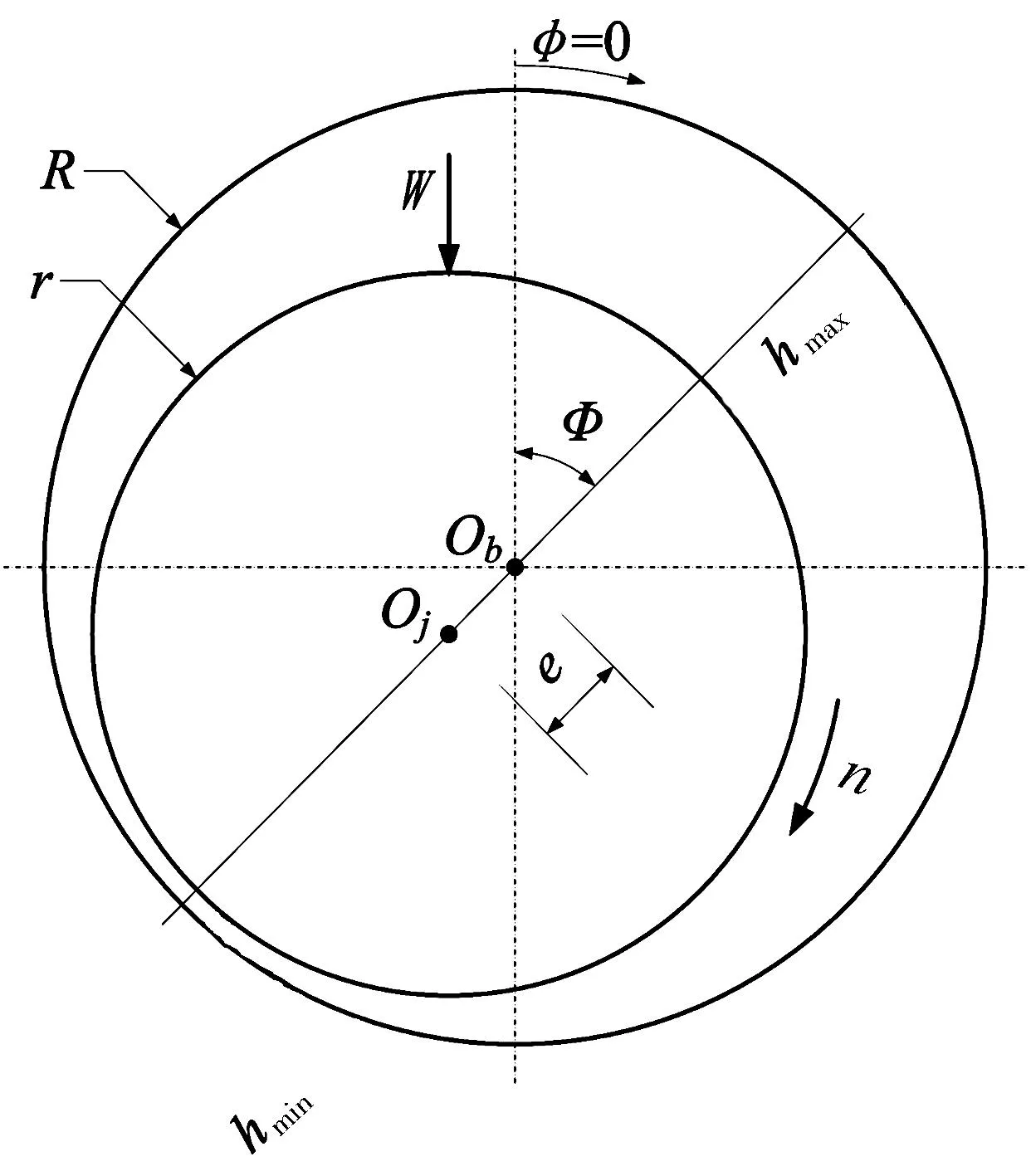
图1 轴颈轴承
在以往的研究中,许多关于轴颈轴承的润滑理论计算都采用了简化的方法,如:无限长和无限短轴承理论;假设轴和轴套都为刚性体,而不考虑变形的影响等。尽管这样会使计算效率提高,但是与实际情况并不相符。例如,当外载荷较大时,偏心率极度增大,使最小油膜厚度大幅减小,由流体润滑理论知识可知,此时的最大油膜压力会变得极大,由此所引起的轴承径向变形也变得不可忽略。
在已有的可变形轴颈轴承润滑问题中,大多采用有限元法、柔度矩阵法或Boussinesq公式计算轴承径向变形,如文献[1-5],其缺点在于计算效率极低、资源损耗过大以及较难考虑偏位角的变化等。在许多情况下,轴承本质上是由一个相对较薄的内衬(轴衬)和其外围包裹的刚性外壳所组成,因此,在忽略剪切力作用的前提下(仅受拉伸或压缩),轴衬在某一点的径向位移,即径向变形,可假设为与该点所承受的压力成正比(弹性本构关系)。Winkler弹性基础模型[6]正是基于此而提出的,它将变形体表示为一系列紧密排列、相互独立的弹性单元,每一个单元都服从材料的线弹性本构关系,从而可利用其求出轴衬的径向变形量,进一步得到相应的油膜厚度变化,再通过数值迭代求解出油膜压力及其他性能参数。该方法已经被成功应用于共形接触副的流体润滑及干接触磨损等问题的求解中,且取得了较有限元方法更为良好的计算效率和相当的计算精确度[7-11]。
本文主要对有限长轴颈轴承展开分析,利用Winkler表面模型求解轴承表面变形,主要研究在定载荷条件下,工况和轴承结构对其偏心率、偏位角、油膜压力分布及油膜厚度等参数的影响规律。此外,在数值模拟过程中使用了压力和膜厚双重迭代的求解方法。该研究成果可为轴颈轴承的设计及其性能计算提供相应的理论参考。
1分析模型
1.1 雷诺方程
适用于普通静载轴颈轴承的二维雷诺方程为
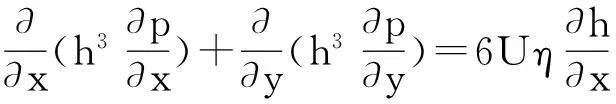
(1)
式中:x为圆周方向,利用有限差分法求解雷诺方程时划分的网格数用m表示;y为轴向,划分的网格数用n表示。数值计算引入雷诺边界条件,即:
p=0(φ=Φ);
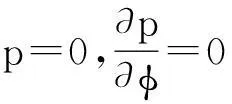
(2)
式中:φ表示以轴承竖直方向为起始位置的周向坐标;Φ为偏位角;φ′为油膜发散区的某一坐标,此处指油膜自然破裂位置。
1.2 弹性变形及膜厚方程
Winkler模型最初是在铁道工程计算中引入的一个假设,本文用来处理轴颈轴承弹流润滑中的固体变形问题,可将其表示为
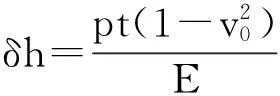
(3)

h=c[1+εcos(φ-Φ)]+δh。
(4)
式中:c为轴承半径间隙,c=R-r,R和r分别为轴瓦内圈半径和轴颈半径;ε为偏心率。
1.3 弹流润滑数值求解流程
为保证数值计算的精度,程序采用膜厚和压力的双重迭代法,即在压力迭代收敛后,还需进行膜厚迭代,直至两者均达到设定精度。通过多次试验,最终设定的计算精度为10-6,既可确保计算的准确性,又不至于过度影响计算效率,程序流程如图2所示。
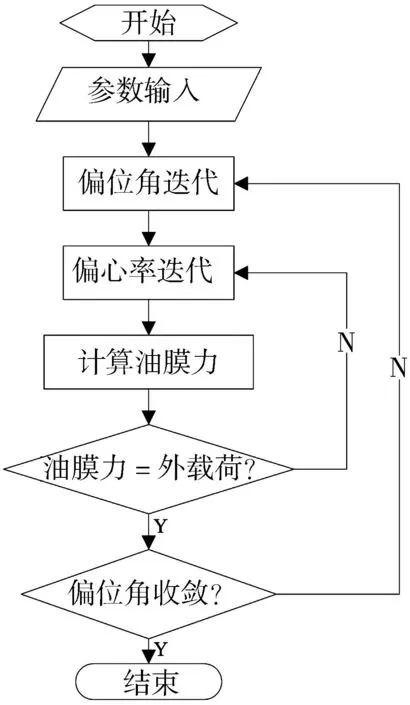
图2 数值计算流程
偏心率的迭代是通过判断外部载荷是否与油膜合力相互平衡来实现的,即当油膜合力小于外载荷时,增大偏心率,而当油膜合力大于外载荷时,减小偏心率,在油膜力和外载荷大小关系发生转换时,则将偏心率的迭代步长减半,否则迭代将不收敛。
通常假定外载荷的方向为竖直向下,如图1所示,则油膜合力的方向应为竖直向上,二者之间的偏差不可太大,这就是偏位角迭代的收敛准则,一般可表示为

(5)
式中:Ft为水平方向合力;Fn为垂直方向合力;γ为计算精度,对于一般问题,设为10-4即可。如果式(5)未被满足,说明预先设定的偏位角Φ不合适,需对其进行修正,对于普通轴颈轴承,一般可用下式[12]修正Φ值:

(6)
2计算结果及分析
图3、图4为不同载荷下的量纲一油膜压力p与油膜厚度H,它们分为刚性与柔性2种情况。可见,在载荷较小时,刚性轴承与柔性轴承两者的油膜压力和油膜厚度相差甚微,而当载荷较大时,两者之间的差距也越大,尤其是最大油膜压力(pmax),这是由于柔性轴承变形使最小膜厚(Hmin)增大,从而大大降低了油膜压力的峰值,使压力分布较刚性轴承更为平缓。此外,考虑与不考虑变形的油膜破裂位置分别为217.3°与210.8°。
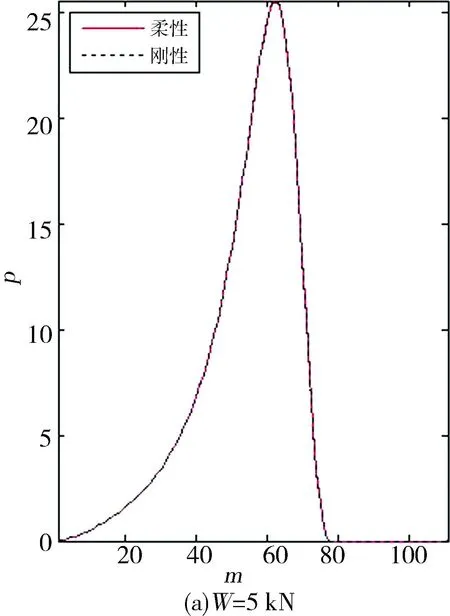
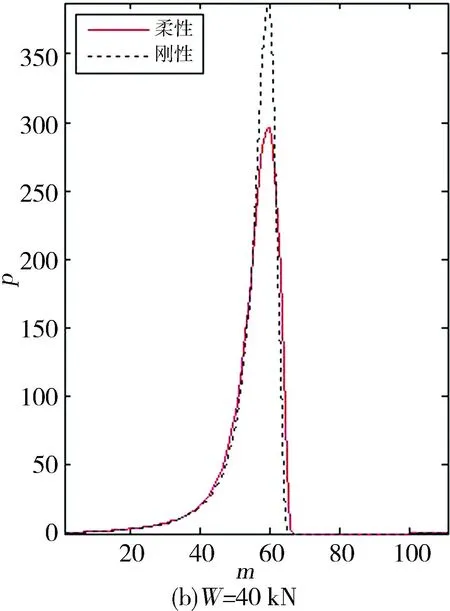
图3 不同载荷下刚性轴承和柔性轴承量纲一油膜压力
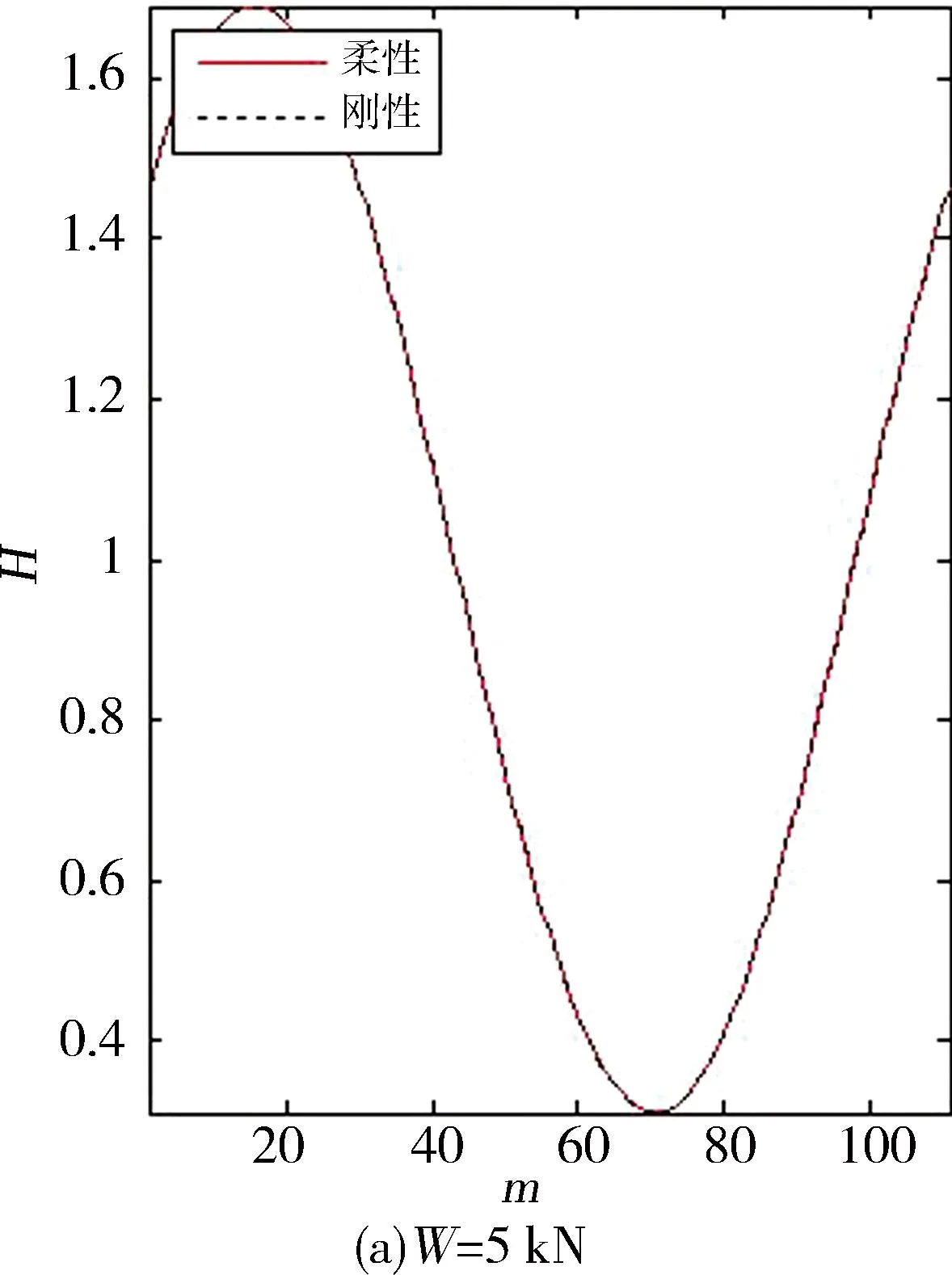
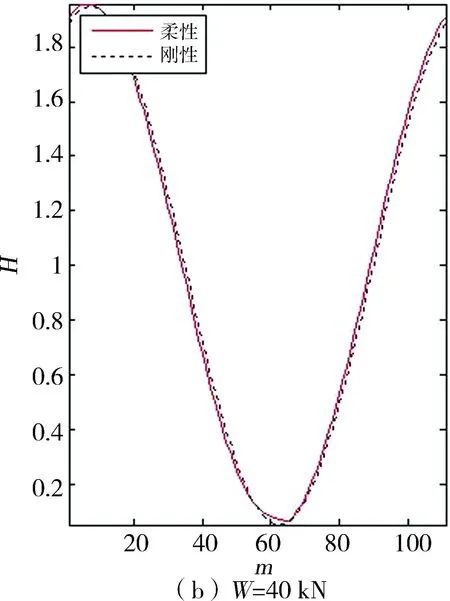
图4 不同载荷下刚性与柔性轴承量纲—油膜厚度
图5定量化描述了载荷变化时刚性与柔性轴承的pmax和Hmin相对偏差。可以看出,pmax与Hmin相对偏差之间的差距随载荷的增大而增大,且当载荷增加为50 kN时,相对偏差均已超过18 %。

图5 刚性与柔性轴承的油膜压力与膜厚相对偏差
以下结果均在考虑轴承表面变形的条件下得到的。图6示出不同载荷和转速对应的轴承偏心率及偏位角。可以看出:定转速条件下,偏心率随载荷的增大而增大,增大的幅度随转速的增大而增大,偏位角则随载荷的增大而减小,减小的幅度随转速的增大亦增大;定载荷条件下,偏心率随转速的增大而减小,减小的幅度随载荷的增大而减小,偏位角随转速的增大而增大,增大的幅度随载荷的增大亦减小。
图7示出不同润滑油运动黏度对油膜压力和油膜厚度的影响。在载荷一定的情况下,黏度越大所对应的油膜压力峰值越小,压力分布则更为平缓,油膜破裂位置也更为靠后(远离压力峰值处),具体的数值可见表1。低黏度润滑油油膜压力峰值的增大是由轴承偏心率的增大而引起的,因此,造成最小油膜厚度的极大减小,相应的最大油膜厚度则变大。
图8示出轴承半径间隙对弹流润滑油膜压力和厚度的影响。初始的间隙越大,最终形成的油膜压力峰值也越大,油膜破裂位置越接近压力峰值处,相应的最小油膜厚度越小,最大油膜厚度越大。不同间隙对应的油膜破裂位置可见表2。另外,在定载荷条件下,不同轴承宽度L和轴颈转速n所对应的油膜破裂位置如表3、4所示。
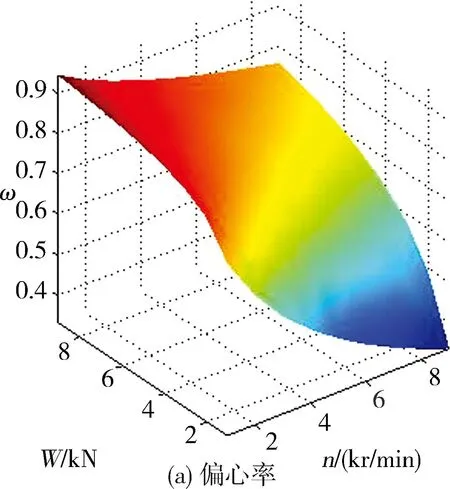
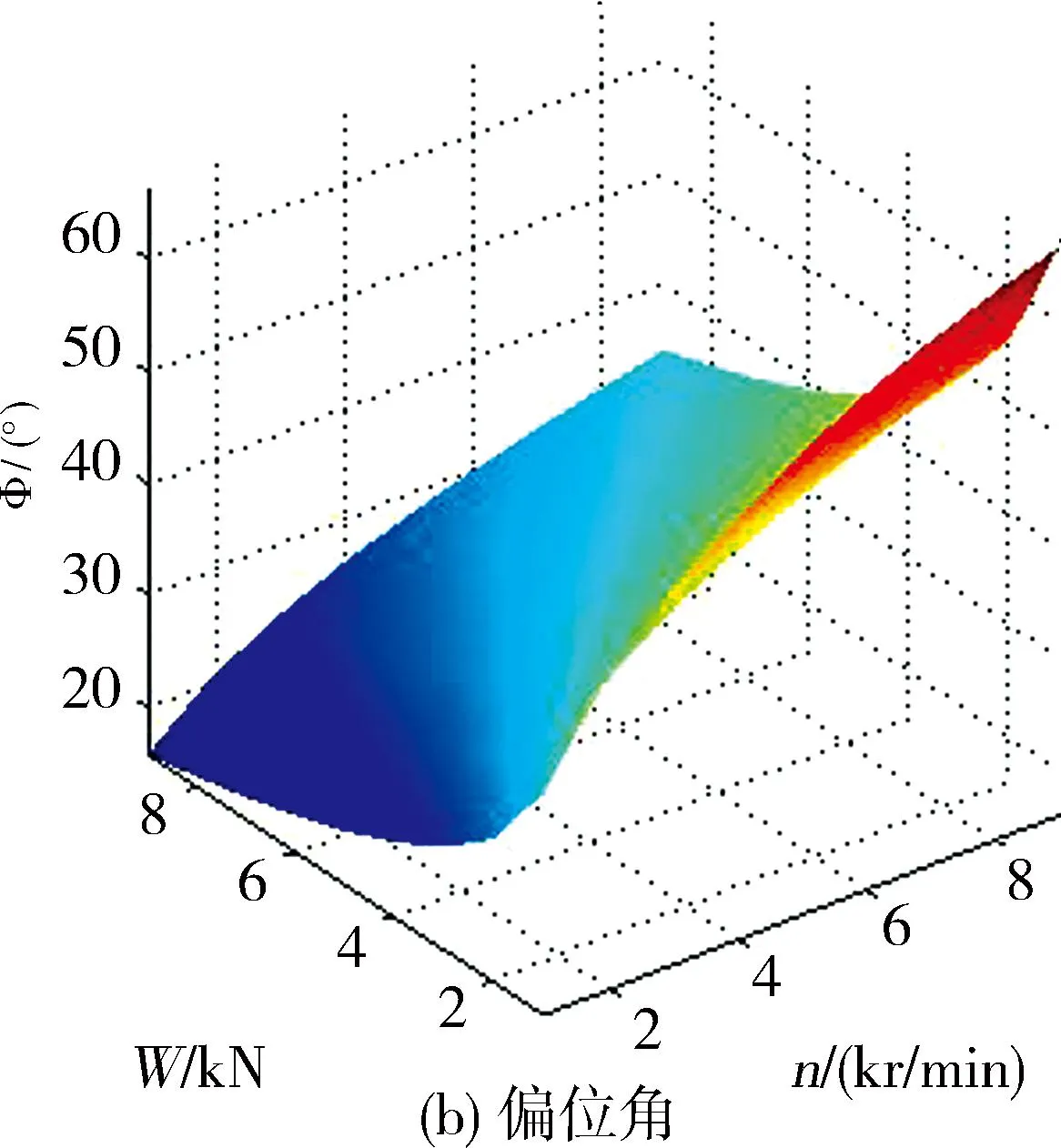
图6 不同载荷和转速下的轴承偏心率及偏位角
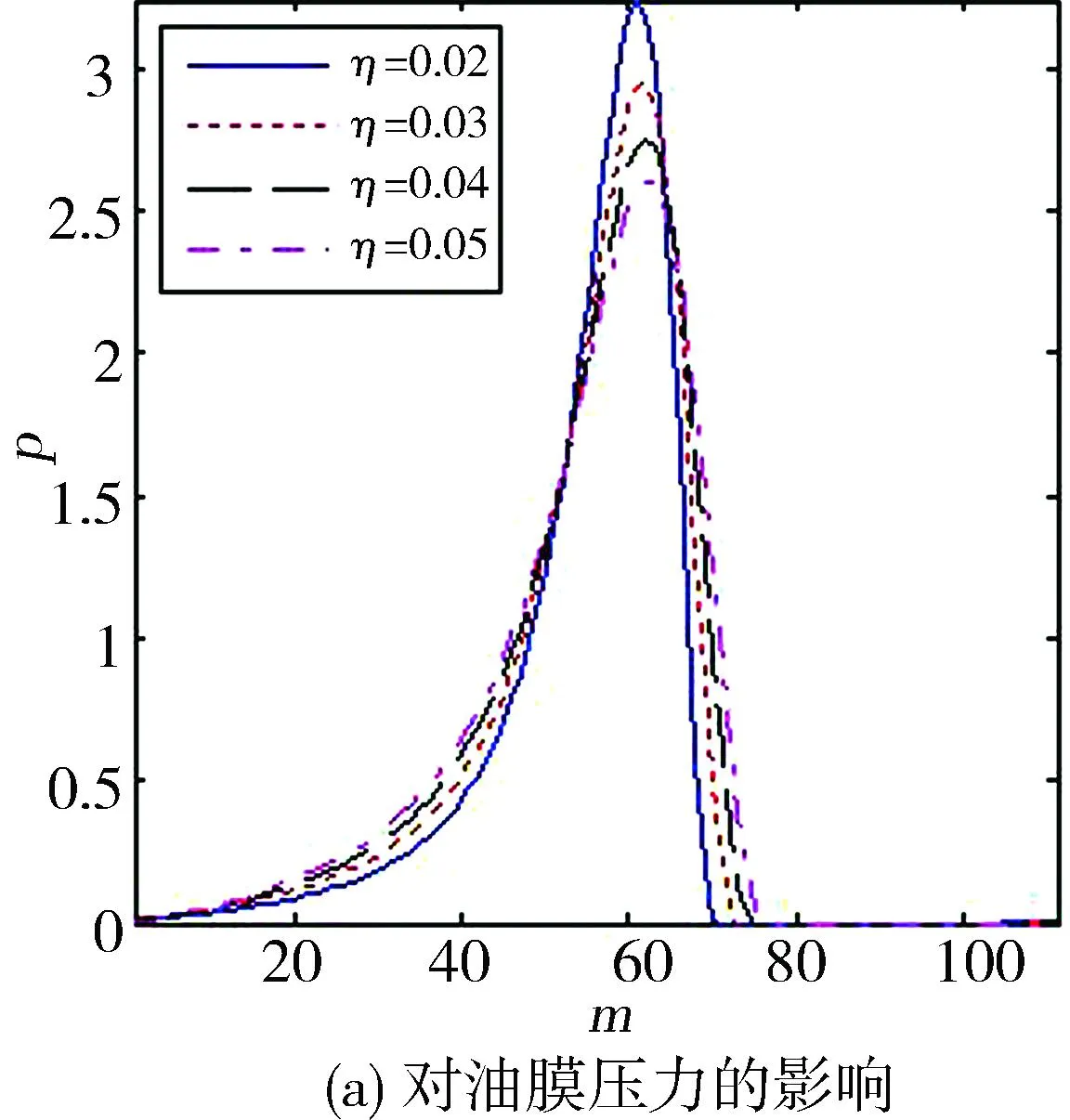
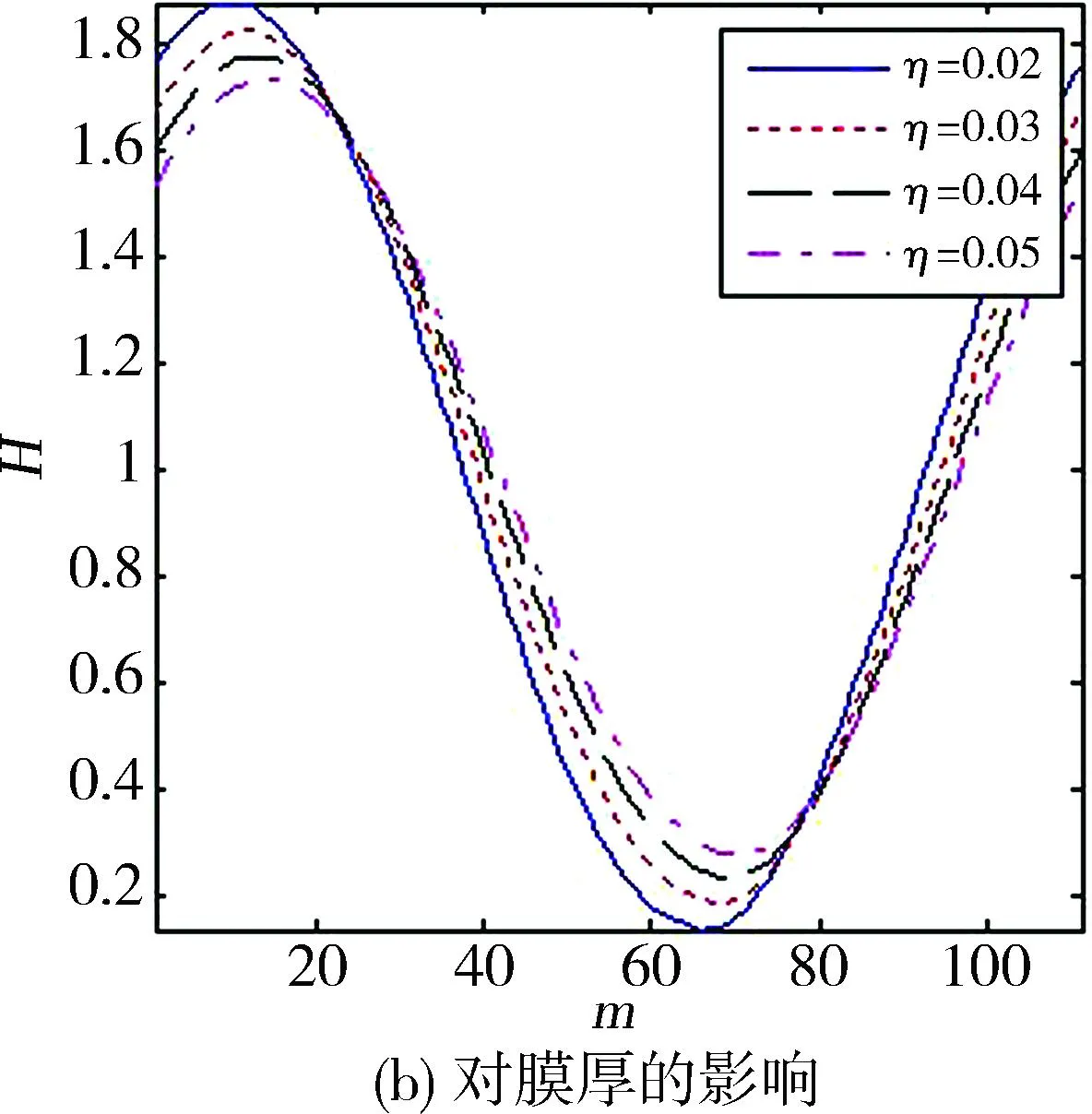
图7 润滑油黏度对油膜压力和膜厚的影响
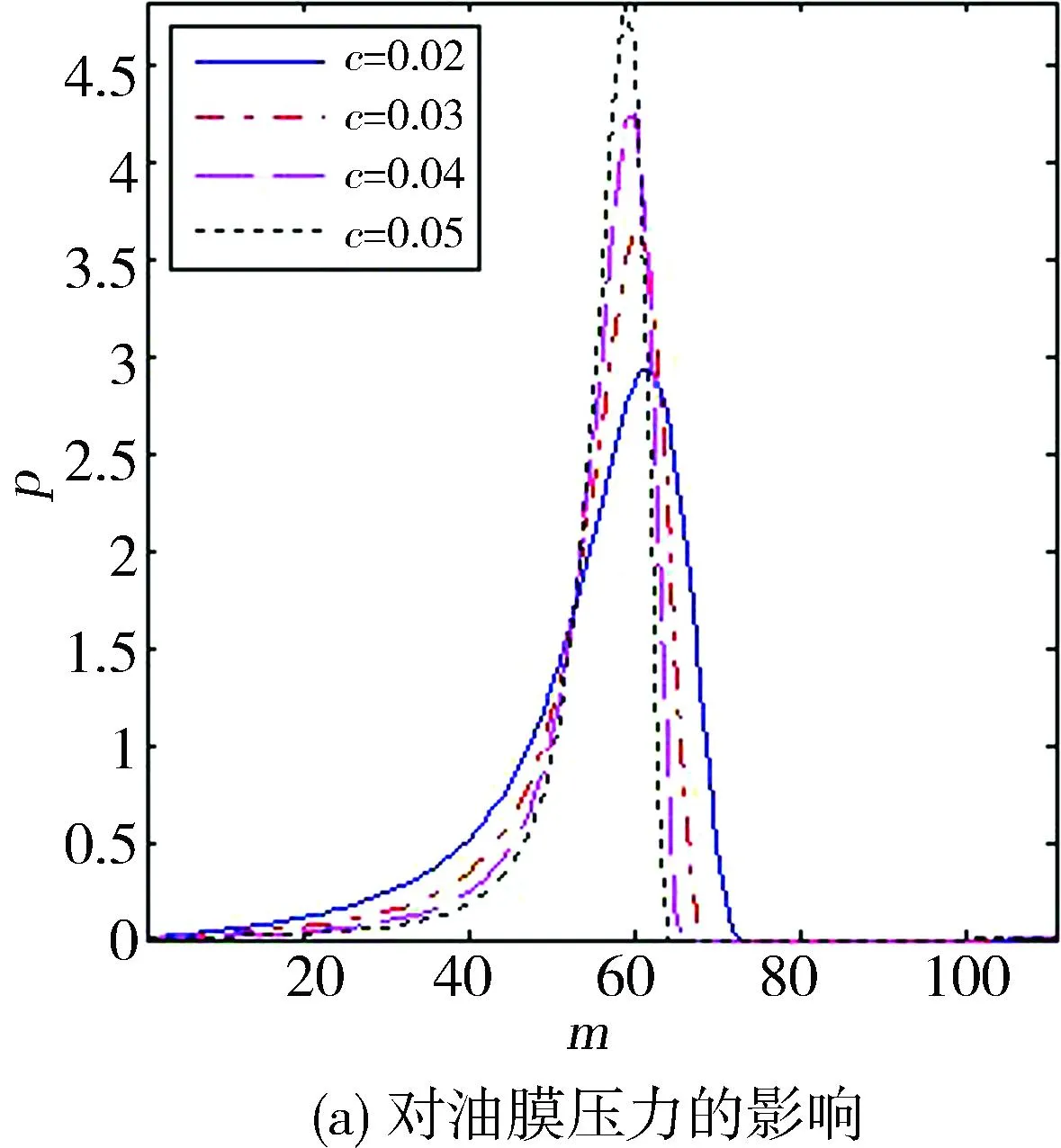
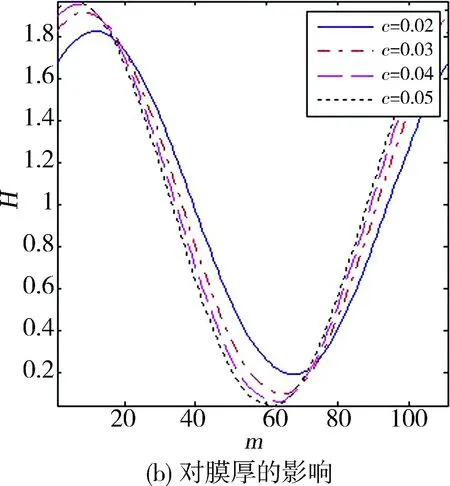
图8 半径间隙对油膜压力和膜厚的影响

η/(Pa·S)0.020.030.040.05位置/(°)230.3236.8243.2249.7

表2 不同半径间隙的油膜破裂位置
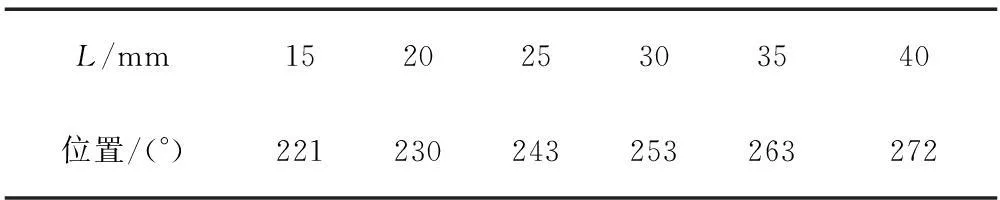
表3 不同轴承宽度的油膜破裂位置

表4 不同轴颈转速的油膜破裂位置
图9示出轴承厚度对油膜压力和膜厚的影响。为使压力的上升与下降状态表达更为清楚,只截取了圆周方向上的中间部分节点进行显示。可以看出,轴承的厚度越厚,其弹流润滑压力峰值越小,压力分布更为平滑,油膜的破裂位置越靠后。图10为图9(b)的局部放大视图。从中可更清晰地观察到,轴承厚度的增大,使最小和最大油膜厚度均增大,这是由于在载荷为一定值的情况下,轴承厚度的增大在某些程度上可以理解为使轴承的弹性模量降低,从而使轴承变形增大,进一步也使得油膜厚度增大。表5为不同轴承厚度对应的轴承偏心率及变形数据。可以看出,轴承厚度对轴承特性的影响几乎呈现出线性关系。
如图11所示,针对不同的轴承弹性模量也进行了一系列模拟,同样是在定载荷的条件下。由图可见,轴承的弹性模量越大,其压力峰值也越大,压力上升与下降的速度越快,因此压力分布更陡峭,而且随着弹性模量的线性减小,压力峰值降低的趋势呈现非线性,降低的速度越来越快。图12是图11(b)的局部放大,可以看出,轴承的弹性模量越小,对应的最小和最大油膜厚度越大。这正是由于越小的弹性模量,使轴承产生的弹性变形越大所导致。不同轴承弹性模量对应的偏心率及变形见表6。可以看出,轴承特性随弹性模量的非线性变化趋势较强。
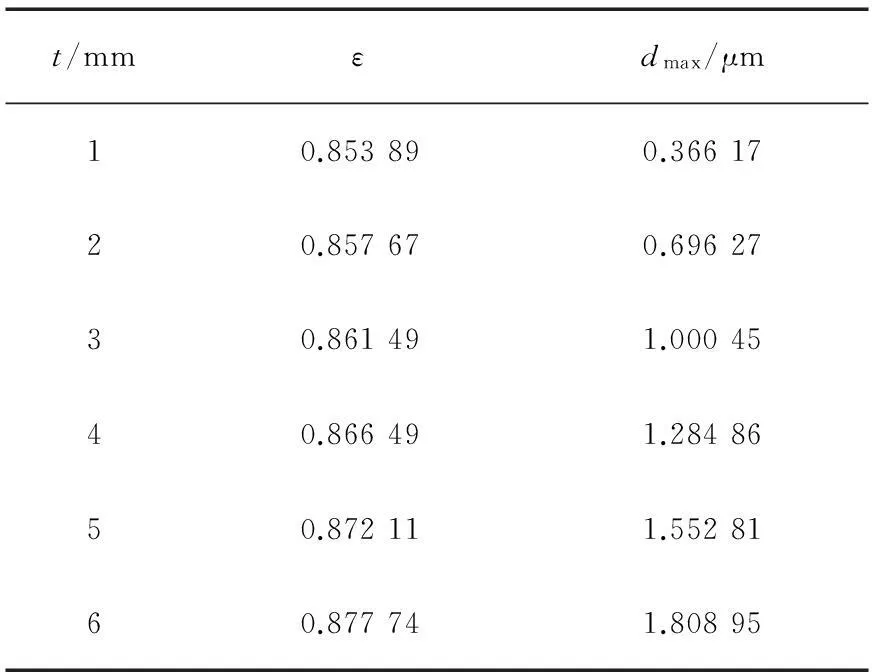
表5 不同轴承厚度的偏心率及变形
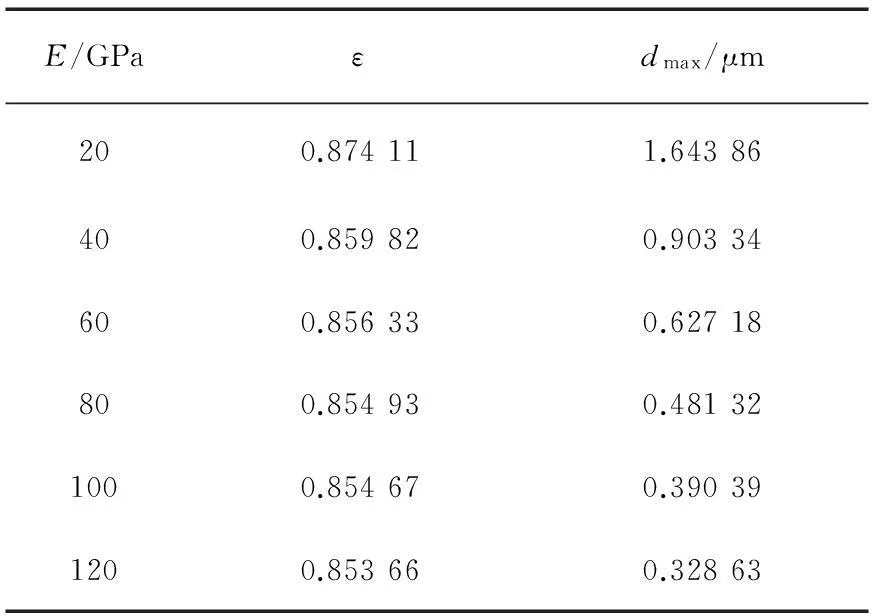
表6 不同轴承弹性模量的偏心率及变形

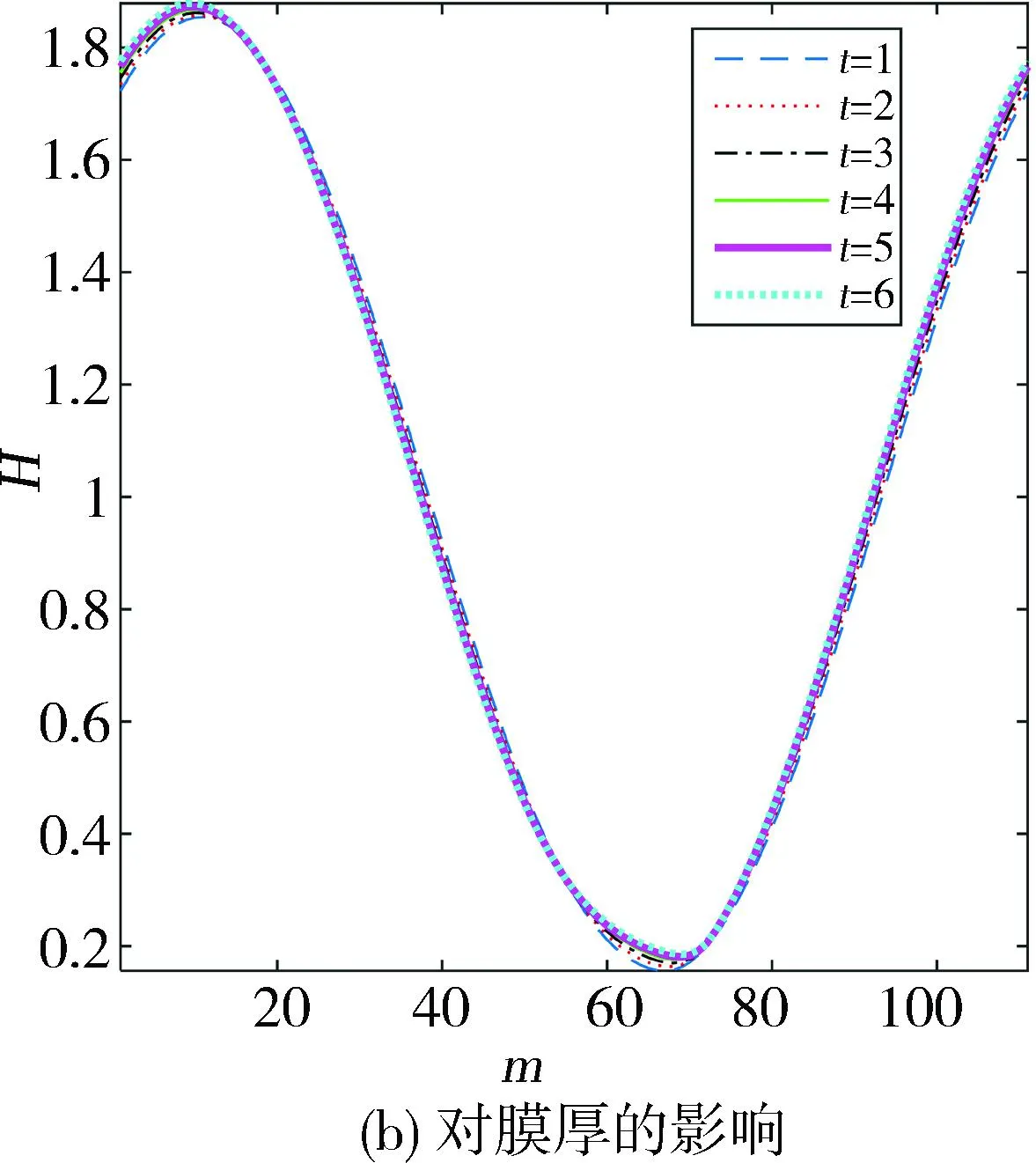
图9 轴承厚度对油膜压力和膜厚的影响
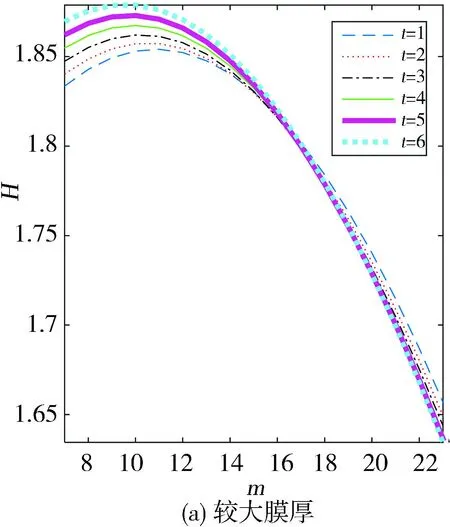
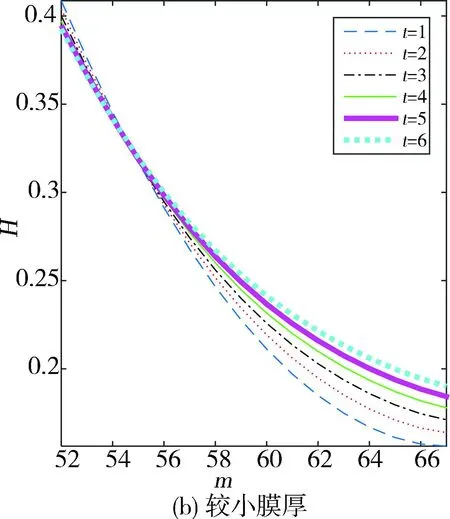
图10 图9(b)的局部放大图
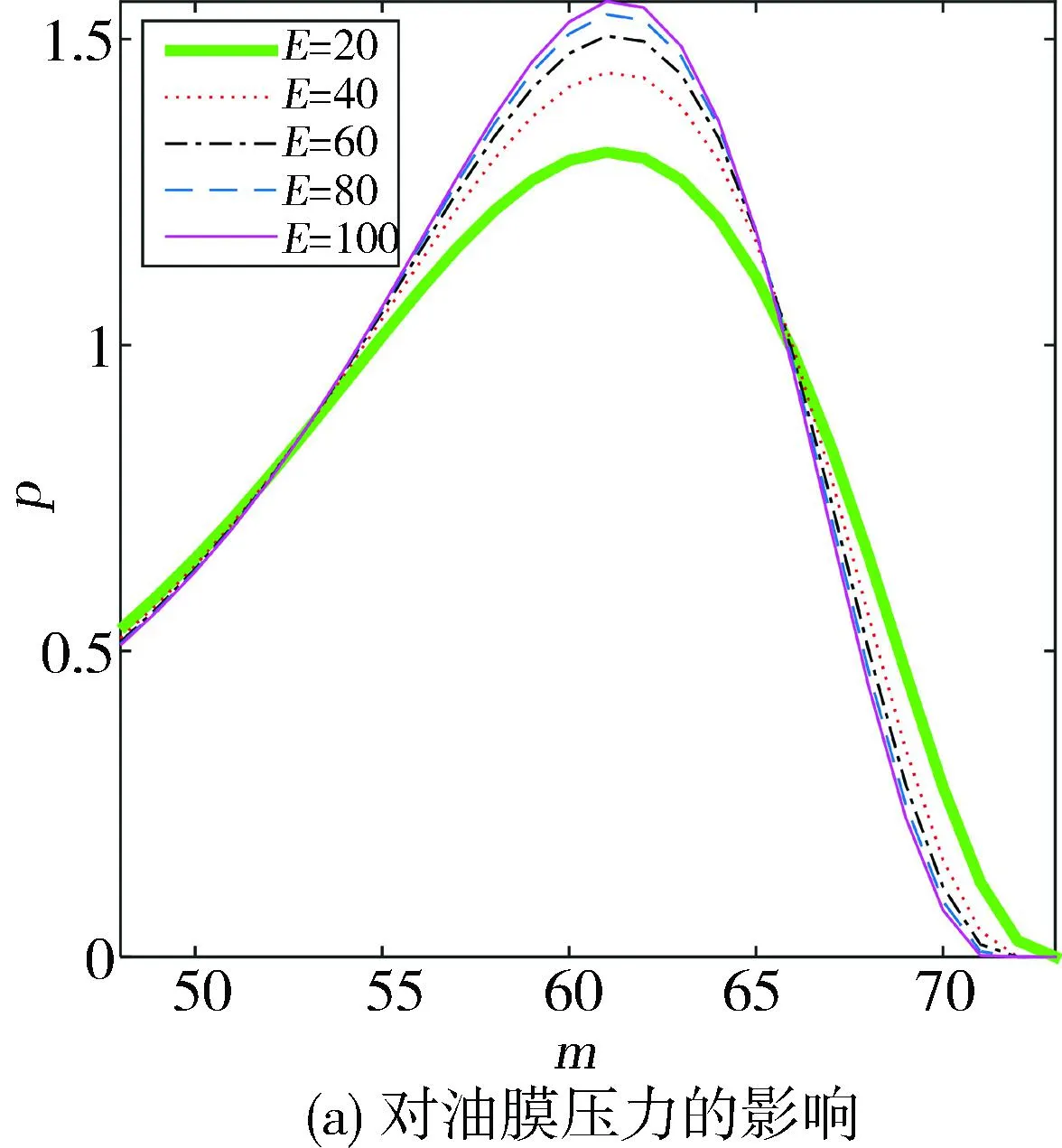
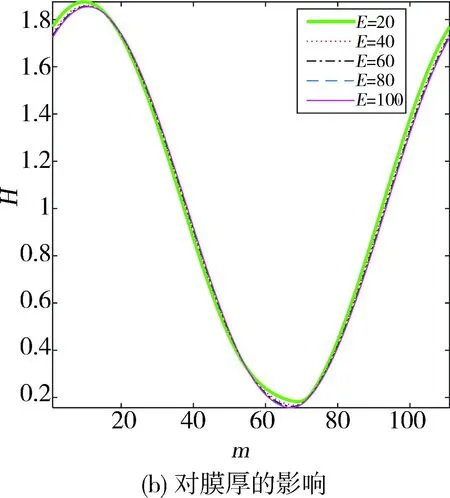
图11 轴承弹性模量对油膜压力和膜厚的影响
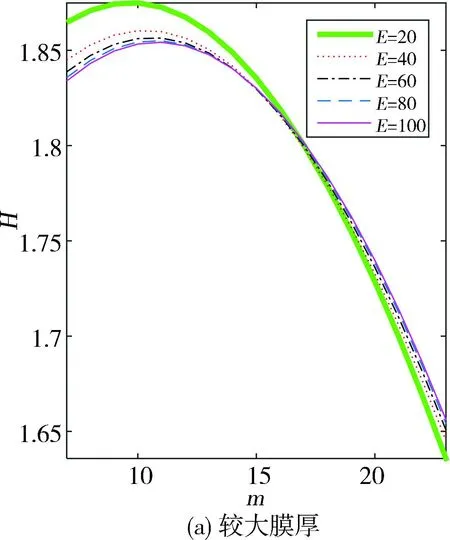
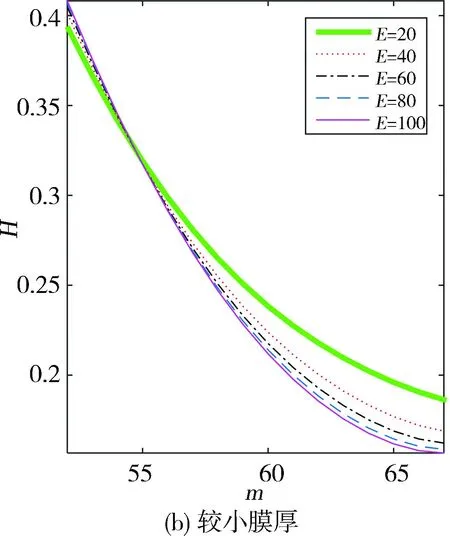
图12 图11(b)的局部放大图
3结论
本文利用Winkler弹性基础模型分析了轴承表面变形对轴颈轴承润滑的影响,通过数值模拟得到了一系列的结果,主要有以下几点。
1)柔性轴颈轴承的油膜压力较刚性的分布更为平滑,压力峰值更小,油膜破裂位置更远离压力峰值处,最小油膜厚度更厚,这种情况在外载荷越大时显得越为突出。
2)轴颈转速与外载荷对弹流润滑轴颈轴承的偏心率及偏位角有不同的影响,具体为:定转速条件下,偏心率随载荷的增大而增大,增大的幅度随转速的增大而增大,偏位角则随载荷的增大而减小,减小的幅度随转速的增大亦增大;定载荷条件下,偏心率随转速的增大而减小,减小的幅度随载荷的增大而减小,偏位角随转速的增大而增大,增大的幅度随载荷的增大亦减小。
3)在定载荷条件下,润滑油黏度越大,形成的最小油膜厚度越大,压力峰值越小,油膜破裂位置离压力峰值处越远;初始间隙越大,偏心率越大,最小油膜厚度越小,压力峰值越大,油膜破裂位置越接近压力峰值处;轴承厚度越厚,其最小和最大油膜厚度越大,压力峰值越小;轴承弹性模量越大,其最小和最大油膜厚度越小,压力峰值越大。
此外,本文提出的有限长轴颈轴承弹流润滑求解可以作为一种通用的方法。如果有可能,在以后的工作中将针对某一类特定的轴套或者使用轴承的机组继续进行深入的研究和探讨。
参考文献
[1]楼志文, 陈瀚, 马晓士. 弹性流体动力润滑理论有限元解[J]. 西安交通大学学报, 1979 (2): 75.
[2]段芳莉, 韦云隆. 用柔度矩阵法对径向滑动轴承的弹流润滑分析[J]. 机械设计与研究, 2000, 16(4): 50.
[3]Xu H, Smith E H. A New Approach to the Solution of Elastohydrodynamic Lubrication of Crankshaft Bearings[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 1990, 204(3): 187.
[4]Liu W K,Xiong S, Guo Y, et al. Finite Element Method for Mixed Elastohydrodynamic Lubrication of Journal-bearing Systems[J]. International Journal for Numerical Methods in Engineering, 2004, 60(10): 1759.
[5]张直明, 吴西柳, 郑志祥. 计入弹性动变形的单块径向轴承可倾瓦动特性[J]. 上海工业大学学报, 1992, 13(3): 189.
[6]Põdra P, Andersson S. Wear Simulation with the Winkler Surface Model[J]. Wear, 1997, 207(1): 79.
[7]Conway H D, Lee H C. The Analysis of the Lubrication of a Flexible Journal Bearing[J]. Journal of Tribology, 1975, 97(4): 599.
[8]Conway H D, Engel P A. The Elastohydrodynamic Lubrication of a Thin Layer[J]. Journal of Tribology, 1973, 95(3): 381.
[9]于如飞, 李培, 陈渭. 一种含间隙铰接副的磨损计算及寿命预测方法[C]// 第十七届中国科协年会论文集. 广州: 中国科学技术协会,2015:1.
[10]Li P, Chen W, Zhu A B. An Improved Practical Model for Wear Prediction of Revolute Clearance Joints in Crank Slider Mechanisms[J]. Science China Technological Sciences, 2013, 56(12): 2953.
[11]宿月文, 陈渭, 郭彩霞. 应用 Winkler 弹性基础模型的间隙铰接副磨损预测[J]. 摩擦学学报, 2012, 32(4): 320.
[12]张直明, 张言羊, 谢友柏,等. 滑动轴承的流体动力润滑理论[M]. 北京:高等教育出版社, 1986: 53.
(编校:饶莉)
The Analysis of Elasto-hydrodynamic Lubrication inthe Finite-length Journal Bearing
YU Rufei, CHEN Wei
(KeyLaboratoryofEducationMinistryforModernDesignandRotor-BearingSystem,Xi’anJiaotongUniversity,Xi’an
710049China)
Abstract:The Winkler elastic foundation model is used to analyze the effect of deformation on the elasto-hydrodynamic of the finite length journal bearing. The dual iteration method of pressure and film thickness is used in the numerical simulation. The results indicate that the differences of oil film pressure and thickness between rigid and flexible bearing increase with the increasing load. Further studies were carried out for bearing surface deformation. The results show that with the increase of the load, the decreasing range of the eccentricity ratio reduces along with the increasing of the rotation speed, and the increasing range of the attitude angle also decreases along with the increase of the rotation speed. However, with the increase of the rotation speed, the increasing range of the eccentricity ratio increases along with the increase of the load, and the decreasing range of the attitude angle also increases along with the increase of the load. Besides that, the effect of the bearing width, bearing thickness, lubricant oil viscosity and clearance on the oil film pressure, thickness and fracture position were investigated under constant load. The findings of this study can provide corresponding theoretical instructions for the design and the performance computation of journal bearing.
Keywords:Winkler model; finite-length journal bearing; elasto-hydrodynamic lubrication; attitude angle; eccentricity
doi:10.3969/j.issn.1673-159X.2016.01.003
中图分类号:TH117.1;TH133.3
文献标志码:A
文章编号:1673-159X(2016)01-0013-06
基金项目:国家自然科学基金资助项目(51175409/E050504)。
收稿日期:2015-07-01
第一作者:于如飞(1987—),男,博士研究生,主要研究方向为滑动轴承及流体力学分析。E-mail:314916049@qq.com
·机电工程·

