基于LAMOST对银河系厚盘恒星轨道偏心率及厚盘形成机制的研究*
景英杰, 杜翠花
(中国科学院大学物理科学学院,北京 101408)(2016年3月15日收稿; 2016年4月13日收修改稿)
自从Gilmore和Reid[1]通过恒星计数方法对银盘恒星数密度的研究引入厚盘以来,越来越多的研究表明厚盘在很多方面有着与薄盘不同的特性.例如:厚盘的标高约为1 kpc,而薄盘约为0.3 kpc;厚盘的平均金属丰度[Fe/H]~-0.6 dex,而薄盘有着偏富的金属丰度,平均金属丰度[Fe/H]~-0.2 dex;厚盘有着比薄盘小的旋转速度和较大的速度弥散.
尽管厚盘的提出至今已经有30多年了,但是对于厚盘的形成和演化依然没有一个一致的解释.目前厚盘的形成模型主要有吸积模型(accretion model)[2]、加热模型(heating model)[3]、富气体并合模型(gas-rich merger model)[4-5]、径向迁移模型(radial migration model)[6]等.吸积模型假设厚盘主要是通过吸积瓦解的卫星星系形成的,Abadi等[2]模拟显示有超过70的厚盘星是这样形成的.加热模型认为厚盘星主要来自在卫星星系并合过程中被动力学加热的前薄盘星(pre-existing thin disk).富气体并合模型采用的假设是厚盘形成于银河系早期气体并合的混乱时代,这里厚盘星主要是在“本地”形成,与吸积模型是很不一样的.径向迁移模型认为薄盘中的星与旋臂发生共振会向外或向内迁移,由于恒星的速度弥散及所处位置与银盘的面亮度相关,从内部向外迁移的恒星会造成银盘加厚.
Sales等[7]提出太阳邻域厚盘星的轨道偏心率分布可以用来限制银河系厚盘的演化模型,一些研究已经用类似方法基于一些巡天数据来研究厚盘的起源.例如:Wilson等[8]基于RAVE (Radial Velocity Experiment)的数据,Lee等[9]基于SEGUE(Sloan Extension for Galactic Understanding and Exploration)的数据.
在本文中我们用LAMOST数据来研究太阳邻域厚盘的偏心率分布并与以上4种模型的数值模拟结果进行对比.
1 数据
1.1 观测数据
郭守敬望远镜(LAMOST,大天区面积多目标光纤光谱天文望远镜)位于中国科学院国家天文台兴隆观测站,是一架有效口径约4 m,视场约5°的“王-苏反射施密特望远镜”.LAMOST有4 000根光纤,可以同时获得4 000个天体的光谱,因此具有很高的光谱获取率.巡天的第2批数据已经释放,其中恒星光谱有3 784 461条,包含有计算出的恒星大气参数以及视向速度(line-of-sight velocity).包括恒星光谱型、金属丰度[Fe/H]、表面重力logg在内的大气参数是通过Ulyss计算[10],而视向速度是交叉匹配恒星光谱和Elodie模版[11]得出的.
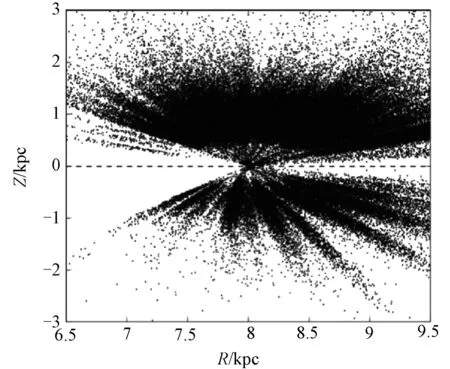
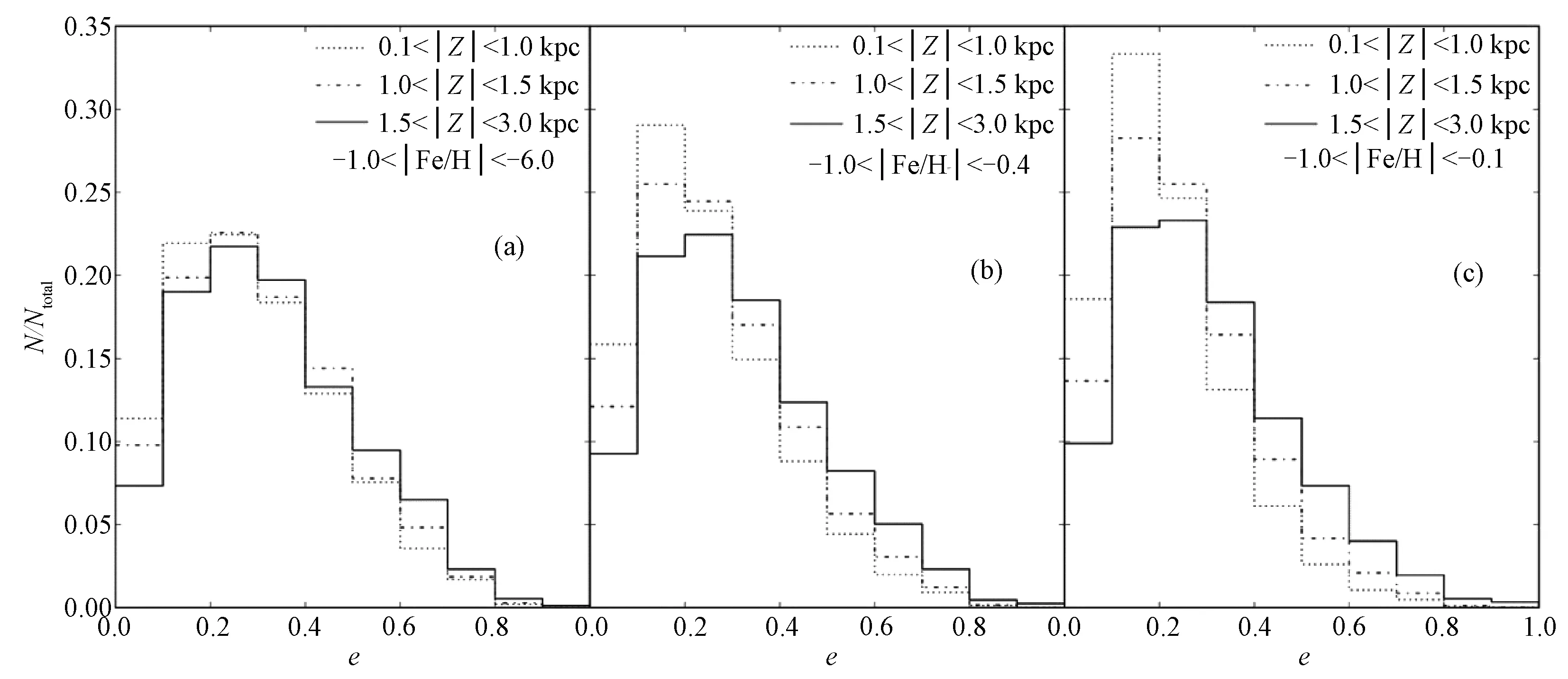
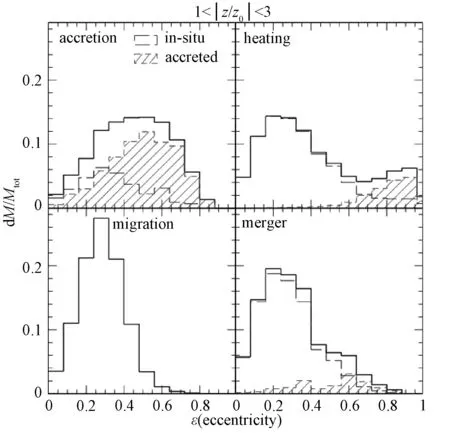
我们采用LAMOST第2批释放数据中的恒星大气参数和视向速度,并基于位置与SDSS 测光数据进行匹配以获得恒星的视星等,恒星的自行则是来自SDSS-POSS自行星表[12-13].接下来,选取一个F/G型的主序星样本,光谱型来自LAMOST,logg大于3.5判定为主序星,并限制样本星光谱g波段的信噪比S/N大于15.为了用分光视差法求距离,限制色指数0.2 Tian等[14]报告LAMOST得出的视向速度与APOGEE有一个 -5.7 km·s-1的系统偏差.我们对比了LAMOST与SDSS-SSPP得出的视向速度,同样基于位置匹配了LAMOST第2批数据(g波段信噪比S/N > 20,logg> 3.5)和SDSS-SSPP(平均信噪比S/N > 20 ) 得到了3 077颗恒星数据,并将结果画在图1中,图中显示LAMOST得出的视向速度与SDSS-SSPP的差值集中在 -6.76 km·s-1, 弥散为7.9 km·s-1.这个系统偏差的原因尚不清楚,在本文中,为了与其他巡天数据相符,我们在LAMOST的视向速度数据上加上6.76 km·s-1. 图1 LAMOST和SDSS-SSPP的视向速度偏移Fig.1 Discrepancies in the radial velocities between the LAMOST pipeline and the SDSS-SSPP 图2 131 353颗样本星在Z-R面的空间分布Fig.2 Spatial distribution in the Z-R plane of the 131 353 sample stars 下面计算恒星的轨道偏心率,我们采用的银河系的引力势来自Paczynski[17],包括核球、银盘和球状晕.恒星轨道偏心率定义为e=(rapo-rperi)/ (rapo+rperi),其中rapo代表恒星运行到距银心最远的距离,而rperi则是恒星运行到距银心最近的距离,我们把恒星现在的位置和速度作为初始条件来计算偏心率.图3显示的是样本星的偏心率e和[Fe/H]的对比分布图,图中显示样本星的金属丰度范围主要在-1<[Fe/H]<0.5,大部分样本星的偏心率e<0.6. 图3 样本星的金属丰度[Fe/H]和偏心率e分布图Fig.3 Metallicity[Fe/H]vs.orbital eccentricity for the sample stars 薄盘、厚盘和晕在空间分布和金属丰度上并没有明确的界限,而是有相互重叠的地方.为了排除晕星的污染,剔除金属丰度[Fe/H]<-1.0的样本星,并且限制旋转速度Vφ>50 km·s-1(Carollo等[18]显示厚盘星平均旋转速度约在180 km·s-1,弥散为51 km·s-1,而晕平均旋转速度在0附近;类似Wilson等[8]限制V>50 km·s-1).为研究薄盘的影响,我们计算了在不同的金属丰度范围和不同垂直距离|Z|的恒星的偏心率分布情况,结果展示在图4中.图4横坐标表示偏心率e,纵坐标表示在对应偏心率范围内样本星数量所占比率.图4的3个子图分别代表恒星金属丰度在-1.0<[Fe/H]<-0.6,-1.0<[Fe/H]<-0.4和-1.0<[Fe/H]<-0.1之间,而图中的点线、点横线和实线分别代表恒星垂直距离在0.1<|Z|<1.0 kpc,1.0<|Z|<1.5 kpc和1.5<|Z|<3.0 kpc之间.厚盘标高约为1 kpc,而薄盘只有约0.3 kpc,因此随着|Z|的增多,薄盘星所占比率减小,在1.5<|Z|<3.0 kpc厚盘占主导,图3显示随着|Z|增大,偏心率小于0.1的恒星比率减小,大于0.3比率略有增加;整体来看恒星所占比率峰值在e=0.1到e=0.3之间,大于0.3的所占比率随偏心率增大而减小,而且没有起伏.金属丰度-1.0<[Fe/H]<-0.6范围内厚盘占主导,薄盘星金属丰度相对偏富[9],因此图4(a)厚盘星占主导(尤其在1.5<|Z|<3.0 kpc范围内),偏心率分布峰值在e~0.2,而图4(b)和图4(c)受薄盘影响逐渐增大,虽然偏心率小于0.2数量有所增加,但峰值以及向高偏心率延伸出一个尾巴(到e~0.8)的趋势没有改变.计算出的偏心率受所选引力势的影响,因此我们对比了采用其他引力势模型(Xue等[19])得出的偏心率,结果显示偏心率的分布没有明显的不同.综上,我们认为厚盘星的偏心率分布峰值约在0.2,大于0.2的恒星数量随偏心率增大而逐渐减小,没有起伏变化. 图4 在不同金属丰度和|Z|区间的恒星偏心率归一化分布图Fig.4 Normalized distributions of eccentricities at different metallicities and within different |Z| ranges 我们把得到的偏心率分布与数值模拟的结果进行对比.之前已有不少对厚盘星轨道偏心率分布的研究,例如Wilson等[8],Lee等[9],分别利用不同的数据和采用不同的引力势模型都得出一致的结果,即厚盘星的偏心率分布峰值在低偏心率处,向高偏心率处逐渐减少,缺乏高偏心率的星,在与模拟结果对比后都认为与吸积过程不符合. 图5取自Sales等[7],表示不同厚盘形成模型模拟得出的厚盘星偏心率分布.图中顺时针从左上开始所采用的数值模拟分别来自Abadi等[2](吸积模型),Villalobos和Helmi[3](加热模型), Brook等[4-5](富气体并合模型)和Roskar等[6](径向迁移模型). 图5 4个厚盘形成模型的偏心率分布图Fig.5 Eccentricity distributions of the four thick-disk formation models 我们得到的厚盘星偏心率分布峰值出现在较小的偏心率处(约为0.2),吸积模型与此不符合,其分布峰值偏大(约为0.5).加热模型虽然在约0.2处有一个峰值,但是在约0.9处又有一个小的峰值,而且e> 0.8的恒星占有不少的比率,这与我们得到的分布不符合,我们的分布缺乏e> 0.8的恒星,而且没有第2个峰值.不过加热模型的第2个峰值主要由吸积引起,而吸积过程与模型中卫星星系的初始条件相关,如果这个位置出现在偏左位置(例如e=0.5),这个峰值可能就表现不出来.相比之下径向迁移和富气体并和模型较为符合我们得到的偏心率分布,尤其富气体模型分布的不对称性更与我们得到的相符合,而径向迁移模型的分布则相对比较对称(符合高斯分布). 厚盘的形成很可能不是一个单一的过程,从上面的结果看厚盘可能主要由富气体并合时期形成,即主要在“本地”形成,而且也有可能受到了径向迁移的影响.当然这里只是比较了太阳邻域厚盘恒星的轨道偏心率分布,其他位置(比如反银心方向)仍需继续研究. 值得注意的是图5中Z的范围对应的是1到3倍的厚盘标高,从第3节来看不同Z范围对低偏心率数量稍微有影响,并不影响偏心率的整体分布(峰值约在0.2,大于0.2的数量随偏心率增大而逐渐减小),因此并不影响我们得出的结论. 在本文中,我们基于LAMOST释放的数据,计算并得到了太阳邻域内(6.5
1.2 样本星的空间速度和轨道偏心率的计算

2 厚盘恒星轨道偏心率的分布
3 与不同模型的模拟结果比较
4 总结

