多传感器对编队目标无源定位的数据关联技术研究
尹明新,武 勇,冀 华
(北京机电工程研究所,北京 100074)
多传感器对编队目标无源定位的数据关联技术研究
尹明新,武 勇,冀 华
(北京机电工程研究所,北京 100074)
针对多传感器对编队目标进行测向交叉定位会产生大量虚假点的问题,提出了一种属性方位联合数据关联方法。采用基于支持度的关联算法对传感器探测到的目标属性数据进行初步关联,剔除部分虚假交点。然后利用改进的基准线最小距离法从候选集合中找出目标的真实测量数据关联集合。仿真结果表明,相对传统的方位数据关联方法,该方法不仅可以快速剔除虚假点,而且能够显著提高关联正确率。
多传感器;无源定位;数据关联;虚假点剔除
0 引言
多传感器无源定位技术具有探测范围广、探测信息丰富的优势,相对于单传感器定位,其速度及精度更高,且对定位平台机动性要求较低。测向交叉定位是多传感器无源定位中应用最多的一种方法,通过多个传感器在不同观测点对目标进行测向,利用测向线的交点来确定目标的位置[1]。但是多条测向线交叉会产生大量虚假点,如何快速、准确地剔除虚假点一直是多传感器测向交叉定位研究中的难点[2]。
目前针对多传感器测向交叉定位中虚假点剔除的研究主要是基于空间数据的,即只利用无源传感器探测到的目标方位数据进行关联,常用的方法有基准线最小距离法[3]、最大似然法[4-5]和拉格朗日松弛算法[6]等。基准线最小距离法算法简单,计算量少,但是在传感器距离目标较远,测角精度不高且目标分布密集等情况下,该方法的关联正确率会大幅降低,且该算法在类聚半径的计算中只用到了候选交点集的一维聚类程度。最大似然法和拉格朗日松弛算法计算量大,不适合实时处理[7]。实际上,在现代化的信息战中,无源传感器不仅能够提供目标的方位信息,而且可以提供用于目标识别的辐射源属性信息,如载频(RF)、重频(PRF)、脉宽(PW)等。在传统的数据关联基础上,利用这些属性信息对测量数据进行关联可以取得更好的关联效果[8]。
本文在参考文献[3]方法的基础上,提出首先利用基于支持度的关联算法进行目标属性数据关联,剔除部分虚假点;其次,采用改进的基准线最小距离法进行方位数据关联,得到正确的测量数据关联结果;最后通过仿真验证了该方法的合理性。
1 测向交叉定位与虚假点产生
测向交叉定位是通过高精度的测向传感器在2个以上的观测点对目标进行测向,通过测向线的交点来确定目标位置的方法。该方法虽然定位误差较大,但因为其全方位和快速的优点,在很多情况下可作为滤波估计的初值获取算法,所以仍然具有重要的研究和应用价值。
在探测区域只存在单个目标的情况下,测向交叉定位问题比较简单。设传感器1(x1,y1)和传感器2(x2,y2)测得的方位角分别为θ1和θ2,根据几何关系可以计算出目标位置(x,y):
(1)
(2)
但是在探测区域内存在多个目标的情况下,测向线相交会产生大量虚假点,如图1所示。虚假点的数量随着传感器和目标数目的增多而急剧增长,数据关联的难度显著增大。当有M个传感器对N个目标进行测向交叉定位时,最多可得到M(M-1)N2/2个交点,而其中只有M(M-1)N/2个真实交点。

图1 虚假点产生示意图Fig.1 Producing false intersection points diagram
因此,剔除虚假点以进行正确的测量数据关联是测向交叉定位首先需要解决的问题。
2 属性数据关联
2.1 支持度函数
理论上,源自同一辐射源目标的属性数据特征值是相同的。但由于传感器存在测量误差,且不同的目标之间也可能存在相似的属性特征,这些都使属性数据测量值与目标之间的对应关系出现了模糊性。属性数据关联就是依据来源于同一目标的测量数据所具有的相似性,采用一定的算法和策略将多传感器获取的多目标的属性数据测量值进行关联。
支持度函数可以将2个属性数据向量之间的相似程度映射为一个概率,即支持度,以支持度的大小作为是否关联的判定准则。不同的构造方法可以得到不同的支持度函数形式,但是作用都是将2个向量的差异度映射到[0,1]区间上,且满足差异度越小,支持度越大的规律。这里采用指数型的支持度赋值函数,如某一传感器测得辐射源的载频为fa,待比较的另一传感器测得的载频为fb,则fa对fb的支持度为
(3)
其中,σfa和σfb分别代表被动雷达对载频f的测量误差的标准差。
2.2 D-S证据理论[9]
D-S(Dempster-Shafer)证据理论是适合目标识别领域应用的一种非精确推理方法,对不确定信息的描述采用“区间估计”而不是“点估计”。在属性数据关联中,将某传感器探测到的某一方向的属性数据向量看作c,将另一传感器探测到的多个属性数据向量看作候选关联集合D,利用支持度赋值函数就可以计算出属性数据向量c在各个参数上对D中各属性数据测量向量的支持度。利用这些支持度,可以融合计算出c对D中各个属性数据向量的总体支持度。
D-S证据理论给出了多组证据的组合规则,采用Dempster组合规则可计算出对D中各属性数据向量的总体支持度。
Dempster组合规则为:
(4)
式中,m(A)表示融合后对事件A的支持度,mi(Ai)表示第i个证据对事件A的支持度,在属性数据关联中即对应着第i个属性参数对2个属性数据向量判定为关联的支持度。
对于某一传感器探测到的1个目标的属性数据向量c,要判断其与另一传感器提供的N组属性数据向量的哪一组相关联,就可以利用上述组合规则,融合c在各个属性参数上分别对N组向量中的属性参数的支持度,得到总的支持度mci(i=1,2,…,N),通过设定相应门限值η,选择有可能的关联组合作为候选观测集,在此基础上,再利用方位数据关联实现不同传感器对同一目标的数据关联。
3 属性方位联合数据关联
3.1 模型假设
假设被动传感器的数目不小于3个,所有传感器和编队目标都在同一平面内,且每个传感器具有全向探测能力和相同的测量精度。
将M个传感器分别对N个目标测得的N条测向线进行编号,设第i个传感器对第j个目标的测向线为Lij(i=1,2,…,M;j=1,2,…,N),表示第i个传感器的第j条测向线。
3.2 算法步骤
属性方位联合数据关联就是利用属性数据对多传感器得到的多个测量向量进行关联,将源自同一目标的不同传感器的测量向量关联到一起,然后利用测量向量中的方位测量信息进行方位数据关联,得到对应同一目标的数据关联结果。算法步骤如下:
1)以第i个传感器对第j个目标的测向线Lij为基准线,则第k(k≠i)个传感器对第l(l=1,2,…,N)个目标的测向线Lkl会与Lij相交,交点为Pkl,ij=(xkl,ij,ykl,ij),并计算出对应的属性数据支持度为mkl,ij,这样的交点理论上有N个。首先对支持度小于门限值η的交点予以剔除。另外,在实际应用中,生成的交点位置有可能超出了传感器的探测范围,也有可能不在相应的探测区域内。按照这3个原则可剔除部分虚假点,提高算法快速性,最后得到交点位置子集Ak,ij,设该子集实际包含q(q≤N)个交点。
这q个交点中只有1个点为Lij与传感器k对目标j的真实交点,其余(q-1)个交点为虚假点。
2)除第i个和k个传感器外,其余的(M-2)个传感器理论上都可能分别与基准线Lij生成N个交点。同样采用上面的3个原则对虚假点进行剔除,分别得到(M-2)个传感器对基准线的交点子集Ar,ij(r=1,2,…,M,r≠i,r≠k),因此这样的子集共(M-1)个。
对基准线而言,除第i个传感器外的其余(M-1)个传感器的所有测向线与基准线最多有N(M-1)个交点,但其中只有(M-1)个交点为真实交点。在传感器无测角误差的情况下,这(M-1)个交点理论上是重合于目标j所在位置的。
3)任选第k(k≠i)个传感器的测向线与基准线Lij的交点子集作为参考子集Sk,ij,其包含p(p≤N)个交点。
4)以参考子集Sk,ij中的每一个交点为参考点,采用最小距离原则分别在剩余(M-2)个子集的每一个子集中选取一个与参考点最近的交点并与该参考点一起组成一个可能的候选真实交点子集Rk,ij。
具体方法为:
设dkl,rs为点Pkl,ij与Prs,ij(r=1,2,…,M,r≠i,r≠k)的几何距离
(5)
式中,Pkl,ij为参考点,Prs,ij是除去参考点集的其余(M-2)个交点子集中的一个点。如果dkl,rl=min{dkl,rs},则将Prl,ij纳入Rk,ij中。因为参考子集含有p个交点,所以这样的候选真实交点子集Rk,ij有p个,每个子集含有(M-1)个交点。
5)因为候选子集Rk,ij包含的(M-1)个点只是第i个传感器的第j条测向线与剩余的(M-1)个传感器的某一条测向线的交点,这些点都在测向线Lij上,它们的一维聚类程度不能完全反映M条测向线所有交点的二维聚类程度,所以本文以每个候选子集Rk,ij的(M-1)个交点为基础,拓展出对应M条测向线的全部n=M(M-1)/2个交点,并计算它们的类聚半径R
(6)
类聚半径R越小说明聚类程度越高,测向线越有可能对应于同一目标,所以选择类聚半径最小的集合为目标j的最终关联集合。
6)分别以第i个传感器的其余(N-1)条测向线为基准线,重复上述过程,即可依次确定出N个目标的正确测量数据关联结果。
4 仿真算例
4.1 仿真条件
假设有3个传感器对6个带有辐射源的编队目标进行侦察定位,目标的各属性数据如表1所示。传感器的位置矩阵M=[-80,-30;-30,-30;20,-30](单位:km),编队目标的位置矩阵T=[-27.5,60;-22.5,60;-17.5,60;-60,70;-45,70;0,70](单位:km),态势分布如图2所示。
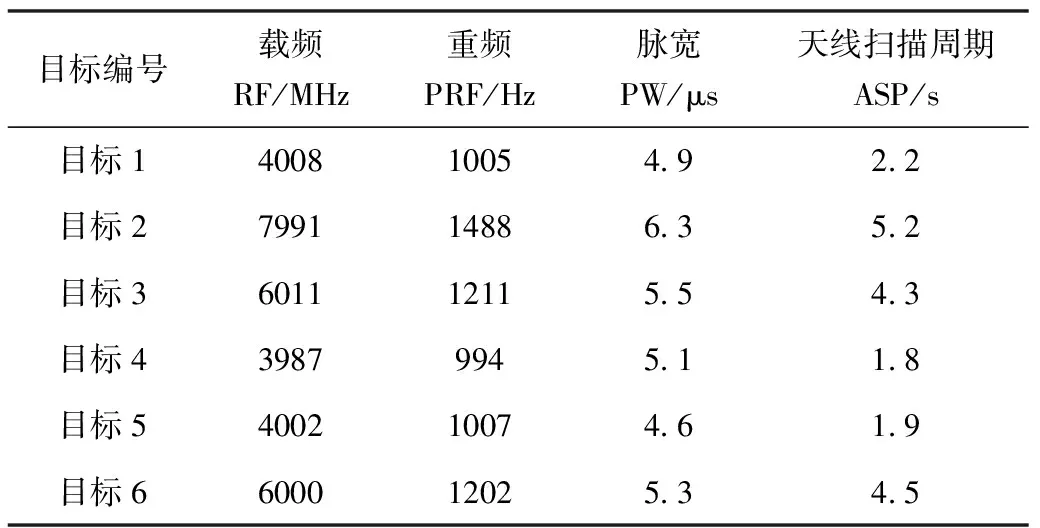
表1 编队目标属性数据

图2 态势分布图Fig.2 Distributing situation diagram
仿真条件表明,目标1、目标2和目标3之间的距离较近,属性数据互不接近;目标1、目标4、目标5之间的距离较远,但属性数据相近;同样,目标3和目标6的距离较远,属性数据相近。
设无源传感器的测角误差标准差为σθ,对属性参数的测量误差的标准差分别为σrf=10MHz,σprf=5Hz,σpb=0.2μs,σT=0.2s,最大探测距离Rmax=200km,属性关联支持度门限η=0.6。
4.2 仿真结果及分析
算例中分别经过1000次Monte-Carlo仿真得到不同目标在不同测角误差条件下的数据关联结果。表2和表3分别为采用传统的纯方位数据关联和联合数据关联算法的仿真结果。

表2 纯方位数据关联正确率
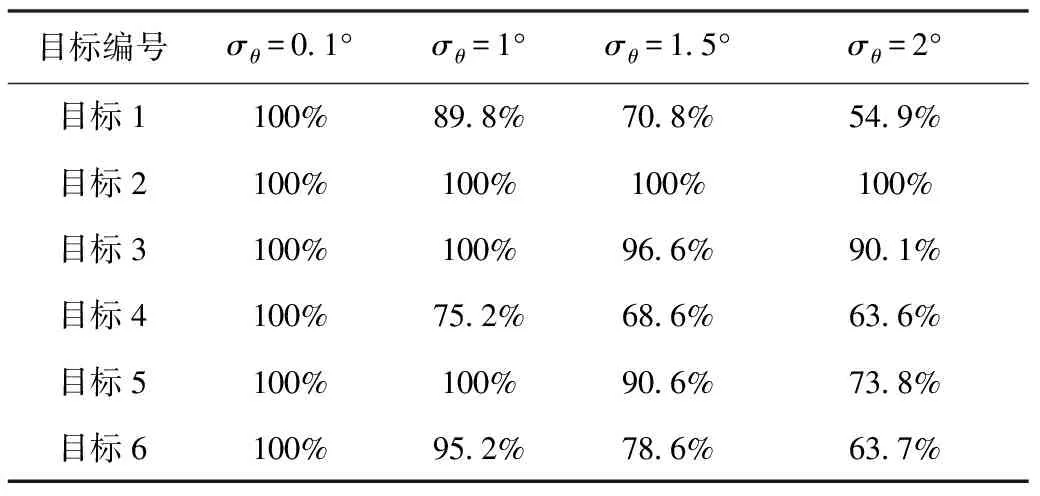
表3 联合数据关联正确率
仿真结果表明,当传感器的测角精度较高时,数据关联正确率较高,且测角误差对正确关联率影响很大,如图3所示。

图3 不同测角误差下的关联正确率(目标1)Fig.3 The association correct rate in different angle measuring errors (Target 1)
从表2中可以看出,采用纯方位数据关联时,目标1、目标2和目标3的关联正确率较低,这是因为在场景设置中这3个目标分布密集,当它们之间的距离与测角误差带来的模糊距离相当甚至更小时,对关联算法里的聚类程度判定影响很大,从而导致关联正确率大幅下降。目标6的关联正确率也偏低,主要也是受算法本身影响,因为如果以传感器1对处于探测区边缘的目标6的测向线为基准线时,其他传感器对所有目标的测向线会与该基准线生成大量虚假点,且分布密集,从而大大增加了数据关联难度。
通过对比表2和表3的仿真结果可以看出,使用属性方位联合数据关联的关联正确率明显高于纯方位数据关联。在场景设置中,目标1、2、3距离较近,测向线交叉时产生的虚假点比较密集,但它们的属性数据互不相近,通过加入属性数据关联后能大大增加其关联正确率。目标1、4、5属性数据相近,利用属性数据关联无法进行判定,但目标分布较为稀疏,所以其关联正确率主要受测角精度的影响。目标3、6的情况与此类似。
5 结论
在复杂的战场环境下,多传感器的数据关联技术是实现编队目标定位的前提和关键。本文在借鉴已有方位关联方法的基础上,提出了属性方位联合数据关联方法,可以快速有效地剔除虚假点,相对于传统的只基于空间数据的关联方法具有更高的关联正确率。研究结果表明,只要目标在属性上或方位上具有较好的可分辨性,联合关联方法就能够得到较好的关联结果,对带有辐射源的编队目标侦察定位具有重要的应用价值。从本文的结果中还可以看出,除传感器的测角误差外,编队目标和传感器的分布特征以及定位距离对采用基准线最小距离算法[10]的方位数据关联的效果也会产生影响。所以,后续还需要针对不同的目标编队特性研究传感器的分布对数据关联结果的影响问题。
[1] 孔云波,冯新喜,鹿传国.多传感器多目标数据关联算法综述[J].中国雷达, 2012, 25(4): 10.
[2] 修建娟,何友,王国宏,等.被动定位系统中的方位数据关联[J].系统工程与电子技术, 2003,25(3): 281.
[3] 李立萍,孟静,陈天麒.一种排除无源交叉定位虚假交点的新方法[J].系统工程与电子技术,1999, 21(4): 20-23.
[4] Popp R L, Pattipati K R , Barshalom Y.m-best S-D assignment algorithm with application to multi-targets tracking [J].IEEE Transactions on Aerospace and Electronic Systems,2001, 37(1):22-37.
[5] Kinlbarajan T, Bar-Sbalom Y, Pattipati K R.Multiassignment for tracking a large number of overlapping objects [J].IEEE Transactions on Aerospace and Electronic Systems, 2001, 37(1):2-18.
[6] Bar-Sbalom Y, Fortmann T E.Tracking and data Association[M].Boston: Academic Press, 1988.
[7] Pattiapti K R,Deb S,Bar-Shalom Y,et al.A new relaxation algorithm and passive sensor data association [J].IEEE Transactions on Automatic Control, 1992, (37)2:198-213.
[8] Deb S, Yeddanapudi M,Pattipati K R,et al.A generalized S-D assignment algorithm for multisensor-multitargets state estimation[J].IEEE Transactions on Aerospace and Electronic Systems, 1997,33(2):523-538.
[9] 蓝金辉,马宝华,蓝天,等.D-S证据理论数据融合方法在目标识别中的应用 [J].清华大学学报, 2001, 41(2): 54.
[10] 修建娟,何友,王国宏,等.两站无源定位系统中的多目标跟踪算法研究 [J].电子学报,2002, 30(12): 60.
Research on Data Association Method in Multi-Sensor Passive Location of Formation Targets
YIN Ming-xin, WU Yong, JI Hua
(Beijing Electro-mechanical Engineering Institute,Beijing 100074,China)
In order to solve the problem of bringing a large quantity of false points in multi-sensor passive location of formation targets, an association algorithm based on feature parameters and azimuth information is proposed. Firstly the association algorithm based on the supports threshold is used to deal with the feature parameters detected by passive sensors in primary association, which can eliminate some false intersection points. Then the modified baseline least distance method is used to find the right location points of target from the spare intersection points sets.The simulation results show that this method can not only eliminate the false points rapidly,but also have a better association correct rate compared with the classical association methods only based on azimuth information.
Multi-sensor; Passive location; Data association; False points elimination
10.19306/j.cnki.2095-8110.2016.06.003
2015-09-10;
2016-01-10。
尹明新(1989 - ),男,硕士,主要从事飞行器导航、制导与控制方面的研究。E-mail: ymxbuaa@163.com
TN957.52
A
2095-8110(2016)06-0012-05

