电动舵系统颤振影响因素分析
宋 涛,熊官送,李邦清,曹东海
(北京自动化控制设备研究所,北京 100074)
电动舵系统颤振影响因素分析
宋 涛,熊官送,李邦清,曹东海
(北京自动化控制设备研究所,北京 100074)
针对电动舵系统颤振问题,将舵系统简化为双惯量模型,并在该模型的基础上分析了舵系统颤振的原因。通过对舵系统传递函数以及单自由度碰撞振动系统力学模型的分析,得出传动机构刚度、间隙等非线性因素以及负载惯量对舵系统稳定性的影响,并分析了各因素造成舵系统颤振的原因。通过数学仿真,验证了所得结论的正确性,并针对颤振抑制提出了相应的改进措施。
电动舵系统;颤振;刚度;负载惯量;间隙
0 引言
舵系统是典型的位置伺服系统,一般由控制器、功率驱动电路、电机、传动机构和反馈电位计等部分组成。而传动机构均会存在一定的间隙和弹性,由多个型号的研制过程可知,传动机构刚度不足、间隙控制不严及负载惯量过大,易导致舵系统发生颤振。颤振是一种自激振动,是由系统内部激发产生的周期性振动[1]。舵系统发生颤振会影响位置控制精度,降低响应的快速性,严重的颤振会破坏系统结构,甚至导致整个舵系统工作失效[2-3]。
针对舵系统颤振问题,国内外许多学者都做出了大量研究。文献[4]通过建立间隙非线性振动模型和极限环模型,利用描述函数法以及摄动法对非线性颤振的规律进行分析和求解,得出了电动舵系统颤振的影响因素,比较准确地解释了电动舵系统中传动机构间隙会引起颤振和较大惯量负载使颤振加剧这一问题。该文仅对间隙引起的非线性动力学特性进行了详细地分析,而对于刚度及负载惯量等影响因素引起颤振的原因未做分析,仅给出了相应规律和结论。文献[5]针对在仿真过程中某型号导弹出现的颤振现象,首先利用描述函数法分析了系统颤振的原因,然后利用超前校正法抑制了颤振现象。该文仅从间隙一个角度分析,未对其他颤振影响因素进行分析。本文针对舵系统颤振的各个影响因素,进行了全面分析,首先建立了舵系统双惯量模型,利用系统传递函数以及对单自由度碰撞振动系统力学模型的理论分析,得出传动机构刚度、负载惯量以及间隙对系统振荡的影响及原因,并通过仿真验证了结论的正确性,最后给出了相应的改进措施。
1 舵系统模型建立
为达到建模目的,须将舵机内部分解为双惯量环节,即电机环节、负载环节,传动机构转动惯量等效到负载环节上。在舵机系统中不能将电机与负载看成一体,否则就是一个简单的刚体运动。间隙、刚度和负载惯量是影响舵系统性能、引起舵面颤振的重要因素,对于实际系统,传动机构间隙不可能完全消除;即便电机与负载是直接耦合的,但传动机构是弹性的,在电机输出力矩的驱动下,传动机构会产生一定程度的弹性变形。因此,非线性环节不能忽略。
双惯量环节模型结构框图如图1所示。其中,KL是传动轴的刚度,i为减速比;当传动轴发生扭转形变时会产生扭矩,称之为轴矩,用Tw表示;Jm、Bm、Tm、θm分别为电机的转动惯量、阻尼系数、电磁转矩和旋转角度;JL、BL、θL分别为负载惯量(包含传动机构),传动机构阻尼系数和负载旋转角度;TL为负载扰动。

图1 双惯量模型的结构框图Fig.1 The model of two-mass transmission system
2 刚度及负载惯量对系统的影响分析
2.1 回路分析
假定舵系统传动机构没有间隙,刚度足够强,电机轴、舵机输出轴均静止。此时输入一激励信号,电机轴开始偏转,而舵机输出轴仍静止,故指令信号与反馈信号出现偏差。舵系统将偏差信号放大以控制电机,电机产生的扭矩经传动减速机构驱动舵机输出轴向偏差角减少的方向偏转。当带动负载(舵面)的舵机输出轴到达指令位置时,由于负载惯量的影响,并不会立刻停下来,而是越过给定值。一旦越过给定值,偏差角信号极性马上改变,因而电机的控制电压极性也发生改变,电机产生的扭矩经传动减速机构驱动舵机输出轴向偏差角减少的方向偏转。在系统阻尼设计恰当时,带动负载的输出轴在指令信号给定值附近左右摆动几次后停止,虽有短暂的调整过程,但不会产生持续振荡。
而实际系统中传动机构刚度有限,均会存在一定的弹性,这样就会使得系统本身存在一定的谐振频率。当信号频率与系统固有的谐振频率相近时,系统会发生颤振;当信号频率与系统固有的谐振频率相同时,系统会发生谐振。电机输出力矩与电机轴角度、电机输出力矩与输出轴角度之间的传递函数分别如式(1)、式(2)所示。
(1)
(2)
这里黏滞阻尼系数Bm、BL很小,为方便分析可认为Bm=BL=0。则电机输出力矩与电机轴角度、电机输出力矩与输出轴角度之间的传递函数化简为:
(3)
(4)
传递函数的左边项,可以看作一个二阶纯惯性环节,是由系统非柔性环节产生。右边项是一个二阶振荡环节,是由系统非柔性环节和柔性环节共同产生的作用。这个柔性系统中存在4个极点,2个位于原点位置,还有1对是复共轭极点。这对复共轭极点的存在使得系统在特点频率下的响应会比较剧烈,从而产生振荡现象。根据式(3)、式(4),可得电机谐振频率为
(5)
电机反谐振频率为
(6)
舵面谐振频率为
(7)
由于:i2Jm≫JL
(8)

(9)
因此影响系统谐振频率的因素(暂不考虑间隙)主要为传动机构刚度KL和负载惯量JL。传动机构刚度减小或负载惯量增加会降低系统谐振频率。
单纯的PID控制之所以不能抑制系统振荡,是因为双惯量系统是四阶系统,而PID控制器最多只有3个可调参数,因此不能自由地配置系统零极点。尽管可以通过增大系统微分参数,等效减小电机转动惯量,降低系统的“惯量比”以增大谐振频率[6],但是微分会放大系统噪声,所以效果有限。要提高系统谐振频率, 必须使传动机构具有较高的刚度。
2.2 数学仿真
根据式(7)可知,系统谐振频率随传动机构刚度的增加而提高。利用MATLAB/SIMULINK对系统进行仿真,固定其他参数(负载惯量为0.044kg·m2,间隙为0),仅改变传动机构刚度,传动机构刚度分别为400、500、800、1000、1600、2000,单位为(N·m)/(°)。得到系统开环幅频特性如图2所示。
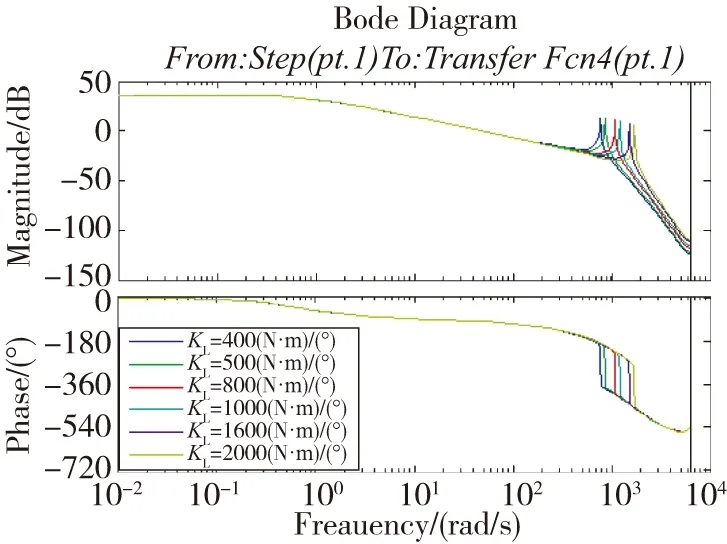
图2 系统开环频率特性与刚度关系曲线Fig.2 Open loop frequency response at different stiffnesses
根据式(7)可知,系统谐振频率随负载惯量的增加而降低。固定其他参数(间隙为0,刚度为500(N·m)/(°)),仅改变负载惯量,负载惯量分别为0.044、0.020、0.010、0.005、0.001、0,单位为kg·m2。得到系统开环幅频特性如图3所示。
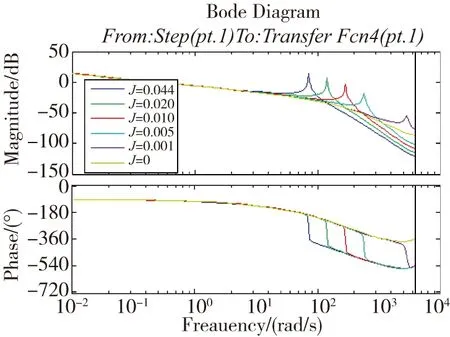
图3 系统开环频率特性与负载惯量关系曲线Fig.3 Open loop frequency response at different load inertia
通过仿真可知,随着负载惯量的增大,系统谐振频率会减小,谐振峰值会增大。因此,负载惯量越大,系统越容易发生谐振。
3 间隙对系统的影响分析
3.1 回路分析
间隙普遍存在于机械产品中,间隙的存在可能引发控制系统极限环振荡,从而引起舵面颤振[7]。舵系统传动机构中的间隙可集中到一处考虑。将传动机构间隙、刚度一起考虑,传动机构的轴矩与间隙耦合,表现为死区特性,如图4所示。

图4 传动机构轴矩与间隙、刚度及转角的关系Fig.4 The relationship between shaft torque, stiffness and degree
由于间隙均位于系统回路内部,其运动过程非常复杂。下面采用单自由度碰撞振动系统的力学模型进行近似分析[8-9],运动模型如图5所示。其中m代表舵面,KL代表传动机构刚度,c代表阻尼系数,e代表间隙,F代表外界干扰力矩。此处以单自由度碰撞振动系统的力学模型探究间隙引起的舵系统非线性振动规律。

图5 单自由度碰撞振动系统的力学模型Fig.5 The mechanical model of a one-degree-of-freedom vibroimpact system
弹簧恢复力为:
(10)
系统振动微分方程为
(11)
若e=0,则系统固有频率为
(12)
若e≠0,设系统固有频率为ωe,发生谐振时振幅为a,则m的位移可近似为
x=asin(ωet+φ)
(13)
忽略阻尼,可解得系统的等效固有频率为
(14)
式(14)中含3个变量-ωe、e、a,无法确定两变量之间的关系,下面通过分析e/a与ωe/ω0的关系(如图6)及e与a的关系,来定性分析ωe、e、a两两之间的关系。
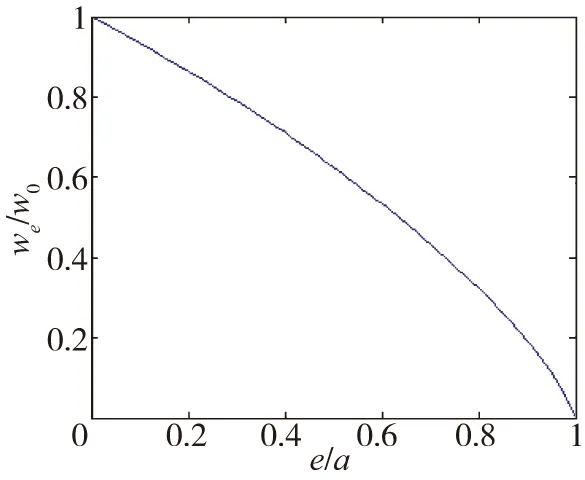
图6 间隙、谐振幅度与谐振频率的关系Fig.6 The relationship between backlash, amplitude and frequency
根据对系统的仿真以及实际系统的测试,ωe随间隙e的增大而减小,但其值变化范围很小,此处为方便分析e与a的关系,认为ωe为常数bω0(其中b为略小于1的常数)。可得
(15)
所以:a=Ce(C为常数)
(16)
由图6可知,当ωe与ω0之比为常数时,e与a之比也为常数,得出与式(16)相同的结论。
以上计算多次采取了近似,与实际系统存在一定的差异。比如在实际系统中,当e等于0时,a有时并不等于0,而是等于一个很小的值;在电机死区及摩擦阻尼适当时,若e不是很大,a可能为0。但e与a的强正相关关系是存在的。
由以上分析可知间隙越大,系统谐振幅度越大,系统也越容易发生谐振。谐振幅度的增大对系统的破坏会更严重。实践证明,控制传动机构间隙是保证系统稳定,提高系统性能必不可少的条件。
也可以将系统传动机构的间隙理解为此处刚度为零,即传动机构刚度为一个分段函数,在前部分刚度为零,在后部分刚度为正常值。间隙的存在大大降低了传动机构刚度,减小了系统谐振频率,使系统更容易发生振荡。但间隙对系统的影响是一个十分复杂的过程,其作用不单单是降低谐振频率,其引发谐振的机理也不能仅从谐振频率的角度进行分析,还需要做更加深入的研究。
3.2 数学仿真
对系统进行仿真,固定其他参数(刚度为500(N·m)/(°),负载惯量为0.044 kg·m2),仅改变间隙大小(间隙为2e),间隙分别为0、0.05、0.1、0.2,单位为(°),得到阶跃响应与舵机间隙之间关系如图7所示。

图7 阶跃响应与间隙之间关系Fig.7 Step response at different backlash
通过仿真可知:间隙越大,系统谐振频率越小,但变化不明显。间隙越大,系统谐振峰值越大,越容易发生谐振,即间隙越大越容易使系统进入非线性共振区。
4 改进措施
由于生产工艺的局限和实际需求,传动机构刚度不可能无限大,负载的惯量和间隙也不可能很小。因此,单纯的增大刚度,减小负载惯量和间隙对谐振的抑制有限,需寻求其他抑制方法。
从频域角度分析,系统发生振荡的根本原因是在特定频率处其幅频特性有较大的增益[10],而陷波滤波器能大大降低系统在某一频率处的幅值,并且基本不影响其他频率处的特性。所以只要事先精确地测得系统谐振频率,然后使用陷波滤波器抑制谐振。而在实际系统中,由于间隙等因素的影响,谐振频率可能会发生变化,所以可采用自适应辨识与陷波滤波器相结合,随时辨识系统谐振频率以更改陷波滤波器的参数。但这种方法计算量大,实际系统中应用较少,而多采用低通滤波的方式。
本文通过设计低通滤波器,在MATLAB/ SIMULINK下对系统进行仿真,验证低通滤波方法的有效性。模型参数设置为:JL=0.044kg·m2,KL=500N/(°),2e=0.15°。采样解算出的位置反馈信号,经过一阶45Hz低通滤波器滤波,滤波后参与回路控制解算。用巴特沃斯滤波器实现45Hz低通滤波。滤波前后仿真结果如图8所示。
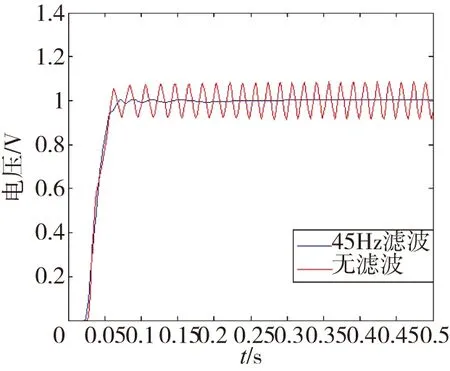
图8 滤波前后仿真结果Fig.8 Different simulation results of the application of the filter
为了验证低通滤波器抑制舵系统颤振的理论分析及数学仿真,在某电动舵系统中,分别对无采用低通滤波器的舵系统进行测试。按控制周期Ts=0.5ms离散化后的滤波器传函为
y(k)= 0.0661x(k)+0.0661x(k-1)+
0.8678y(k-1)
(17)
其中,x为滤波前数据,y为滤波后数据;(k)为当前周期值,(k-i)为前i个周期值。以单位阶跃信号对舵系统进行测试,测试结果如图9、图10所示。
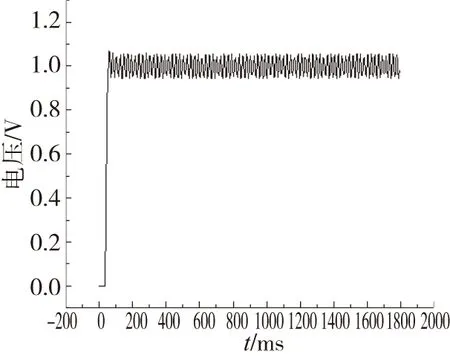
图9 未采用滤波器时舵系统的单位阶跃响应Fig.9 Step response before using the filter
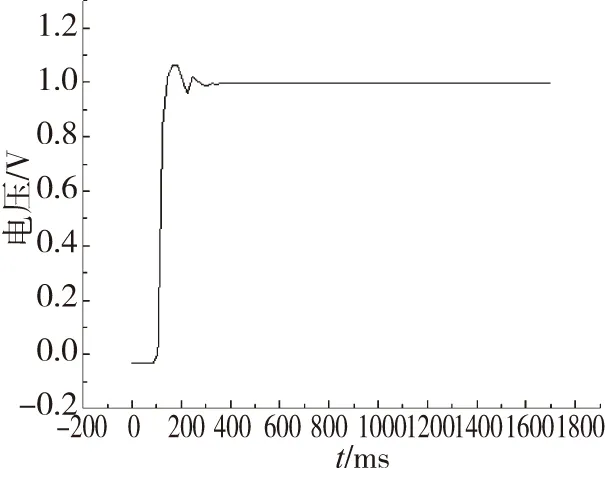
图10 采用滤波器后舵系统的单位阶跃响应Fig.10 Step response after using the filter
通过单位阶跃响应曲线可以看出,在未采用滤波器时,舵系统发生振幅约为0.15V、频率约为50Hz的颤振。在采用滤波器后,系统响应虽有一定的超调和半波振荡,但最终趋于稳定。对于抑制舵系统颤振,低通滤波法是一种简单可行的方法,其通过滤掉引发系统颤振的频率信号来抑制系统颤振,仿真和试验结果表明,低通滤波法具有一定的工程应用价值。
5 结论
本文通过对舵系统双惯量模型的建立,利用系统传递函数以及对单自由度碰撞振动系统力学模型的理论分析,得出传动机构刚度、间隙以及负载惯量对系统振荡的影响及原因:从频域角度分析,系统发生振荡的根本原因是在特定频率处其幅频特性有较大的增益。传动机构刚度越小、负载转动惯量越大、间隙越大,则系统谐振频率会越低,系统也就越容易发生振荡,仿真结果证实了理论分析的正确性。采用低通滤波器能有效抑制舵系统颤振,仿真和试验结果验证了其有效性。
[1] 许行之,高亚奎,章卫国. 考虑舵机动力学的舵回路系统颤振特性分析[J].计算机仿真,2014,31(10):80-85.
[2] 陈鹏展,唐小琦,金宏星. 伺服系统速度环控制参数自整定方法研究[J].仪表技术与传感器,2010(2):78-81.
[3] 赵忠胜. 浅谈数控系统振荡的排除方法[J].机床电器,2006,33(1):25-26.
[4] 张新华,谢劲松,李邦清. 电动伺服机构振荡问题研究[J].航天控制,2010,28(3):83-88.
[5] 李友年,陈星阳. 舵机间隙环节对控制系统的影响分析[J].航空兵器,2012(1):25-28.
[6] 胡华. 柔性伺服系统振荡抑制算法研究[D].哈尔滨:哈尔滨工业大学,2011.
[7] 张明月. 滚珠丝杠式电动舵机非线性分析及控制策略研究[D].中国科学院研究生院(长春光学精密机械与物理研究所),2014.
[8] Xu J. The analysis of grazing periodic motions in a single degree of freedom vibro-impact system with double constrains[J].Pure Mathematics , 2015, 5(4):121-128.
[9] 朱喜锋,罗冠炜. 两自由度含间隙弹性碰撞系统的颤碰运动分析[J].振动与冲击,2015,34(15):195-200.
[10] Odai M,Hori Y. Speed control of 2-inertia system with gear backlash using gear torque compensator[C].IEEE AMC Coimbra,1998:234-239.
Study on Impact Factors of Chattering in Electromechanical Actuator
SONG Tao, XIONG Guan-song, LI Bang-qing, CAO Dong-hai
(Beijing Institute of Automatic Control Equipment,Beijing 100074,China)
To avoid chattering in electromechanical actuation system, the system model is simplified as a two-mass transmission one, and the causes for chattering are analyzed on the basis of the model. By analyzing the transfer function of the actuator system and the model of a one-degree-of-freedom vibroimpact system, the way the load inertia and the nonlinear factors like servo drive stiffness and backlash impact on the performance of the system is discussed. The results of simulation show that the theory could explain the causes of the chattering in electromechanical actuator. Measures are put forward for the suppression of the chattering.
Electromechanical actuator;Chattering;Stiffness;Load inertia;Backlash
10.19306/j.cnki.2095-8110.2016.06.009
2015-05-26;
2015-06-28。
宋涛(1990 - ),男,硕士,主要从事伺服系统控制方面的研究。E-mail:18510970869@163.com
TP273
A
2095-8110(2016)06-0045-05

