基于间接法的上升段轨迹优化方法研究

吴嘉梁

(北京机电工程研究所，北京100074)

基于间接法的上升段轨迹优化方法研究

吴嘉梁

(北京机电工程研究所，北京100074)

固体火箭上升段轨迹优化设计具有重要的工程意义。针对此问题，提出了一种求解上升段最优轨迹的可行方法。在零侧滑角假设下构建飞行器模型，以推力方向为最优控制量，根据极小值原理推导一阶最优条件。采用间接法，将真空条件下上升段最优轨迹的解作为初值，以状态响应方程构造一种迭代的方法，最后在满足攻角过程约束下，通过同伦算法获得真实大气环境下的最优轨迹。仿真结果表明，该优化算法能够稳定收敛，具有良好的鲁棒性。

固体火箭；上升段；最优控制；轨迹优化；间接法

0 引言

固体火箭由于具有准备时间短、机动性强的优点，近年来应用越来越广泛，并且随着其发射任务的多样化和复杂化，在飞行中面临着更强的过程约束与终点状态约束，这就突出了上升段轨迹优化设计的迫切需求。直接法和间接法是轨迹优化最常用的两种方法。间接法是基于庞德里亚金极小值原理推导最优控制的一阶必要条件，构成了求解最优轨迹的Hamiltonian边值问题(HBVP)，由于不对性能指标函数直接寻优，因此称为间接法；直接法采用参数化方法将连续空间的最优控制问题求解转化为一个非线性规划(NLP)问题，通过数值求解非线性规划问题来获得最优轨迹。

Lu提出了一种采用有限差分法求解最优轨迹的方法，并对该方法进行了进一步的研究和发展[1-3]，宣颖等采用伪谱法进行上升段飞行器轨迹优化，能够获得正确有效的最优轨迹[4-5]，Dukeman采用打靶法来求解轨迹优化的两点边值变分问题，获得上升段飞行器最优轨迹[6]。综合以上研究结果可以看出，直接法在求解优化问题时，有着初值敏感度较低且收敛域更广、不必推导一阶最优性条件的优点，但是也有易收敛到局部最优解、求解速度慢的缺点；间接法在求解最优问题时，具有解的精度高、最优解满足一阶最优性必要条件、求解速度较快的优点，但是相对于直接法，间接法对初值的选取较为敏感。因此，本文基于间接法，建立飞行器轨迹优化模型，采用真空解为初始猜测，并通过状态响应方程迭代的思想求取最优轨迹，通过仿真验证算法的收敛性。

1 飞行器动力学模型

鉴于传统基于地球固连坐标系下的三自由度动力学方程在利用最优控制理论推导协态方程时十分困难，为了提高算法效率，本文基于地心惯性坐标系建立飞行器的三自由度动力学方程：

(1)

在式(1)中，R∈R3为地心惯性坐标系下地心到质心的向量，称为矢径向量，V∈R3为地心惯性坐标系下速度向量，g(r)为重力加速度项，T为推力大小，m(t)为飞行器当前时刻的质量，Isp为比冲。lb为飞行器体轴方向单位向量，ln为飞行器纵对称面内法向方向单位向量，A和N分别为气动力在lb与ln上的投影。

在本文上升段制导研究中，认为飞行器的主对称面和由单位矢量lb与飞行器空速向量Vr确定的平面始终保持重合，即侧滑角始终保持为零。根据上述定义，已知弹体轴矢量lb和空速矢量Vr的条件下，定义弹体y轴空间矢量为ly

(2)

其中，‖lVr×lb‖=|sinα|，lVr=Vr/‖Vr‖是Vr的归一化矢量，Vr=V-ωE×R-Vw，V为惯性速度矢量，ωE为地球自转速度向量在地心惯性坐标系中的投影，Vw为风速矢量，由于风速是不可知的，故在动力学模型中设Vw恒为0。

通过lb、ly和lVr可以得到弹体法向单位方向矢量ln和攻角α为：

ln=-lb×ly

(3)

(4)

通过式(2)、式(3)的定义可以确保飞行器在攻角正负变化时不会出现180°的滚动角跳变。之后将地心惯性系下的弹体坐标系各轴空间矢量投影到地理系下，可以得到三个弹体姿态角：

lbt=Titlb,lnt=Titln

(5)

ϑ=tan-1(lbty/lbtx),

(6)

其中，lbt、lnt分别代表地理系中lb、ln的投影，Tit为地心惯性坐标系到地理坐标系的转换矩阵，ϑ、ψ、γ分别代表俯仰角、偏航角和滚动角。

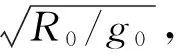
(7)

2 最优控制问题求解

2.1 最优控制模型

飞行器轨迹优化问题本质上是一个最优控制问题，即在多种约束的限制下，找到一个最优推力方向，使得在此过程中轨迹的某个性能指标最优。本文选取终端速度最大，即终能量最大作为性能指标

J=‖Vf‖

(8)

定义哈密顿函数为

(9)

其中，P∈R3为速度对应的协态变量，Q∈R3为矢径对应的协态变量。选取弹体纵轴方向lb为控制量，根据庞德里亚金极小值原理，最优驻点条件为

(10)

(11)

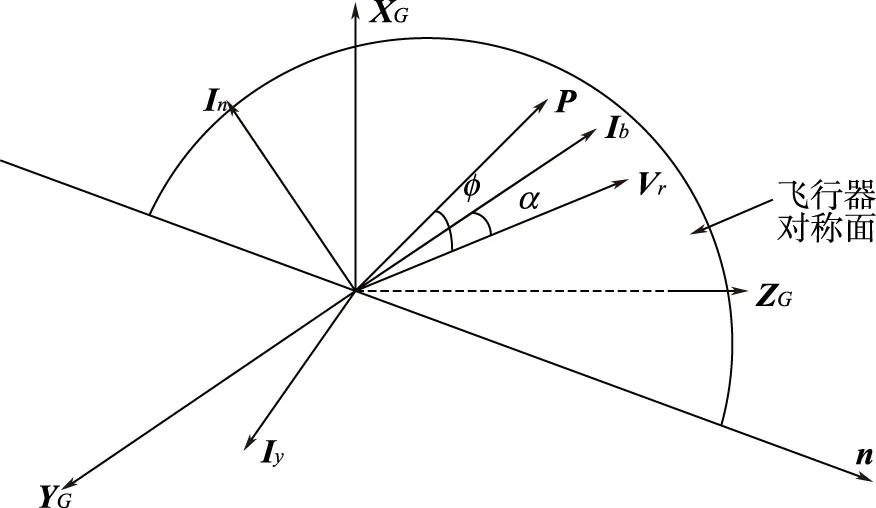
图1 矢量示意图Fig.1 Figure of vector

(12)

可以得到最优攻角方程为

(13)

由式(13)通过一维数值搜索方法可以求出最优攻角，之后带入式(11)即可得到最优弹体纵轴方向。

根据动力学方程列写正则方程为

(14)

得到协态变量的微分方程：

(15)

(16)

2.2 过程及终端约束

为了实现飞行器终端的位置和姿态要求，本文建立末端时刻固定的终端约束方程

(17)

其中，rfs为终端高度约束，Rf为终端位置，Vf为终端速度，lf=Rf×Vf。并由最优控制理论可得横截条件

(18)

由式(18)易得如式(19)所示的包含状态与协态变量终端值的等式

(19)

同时考虑飞行器实际结构强度的要求，引入攻角过程约束：

C1=α-α0≤0

C2=-α-α0≤0

(20)

在式(20)中，显含控制变量lb(攻角α为lb和lVr的函数)，根据极小值原理，当约束触发时有：

(21)

其中，λα为攻角约束α对应的增广乘子，为得到式(21)的完整表达式，要求得λα。在满足约束时，λα=0；当不满足约束时，最优驻点条件变为

(22)

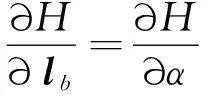
(23)

2.3 最优轨迹求解

为了获得需要的最优轨迹，本文根据正则方程的形式，基于状态响应方程的思想设计了一种迭代方法来求取最优轨迹。定义

(24)

则正则方程变为：

(25)

(26)

其中：

N[cosφ-cosαcos(φ-α)]}

(27)

{-Acos(φ-α)+

N[cosφ-cosαcos(φ-α)]}

(28)

根据状态响应方程

(29)

通过选取合适大小的τ，使积分项用分段常值函数代替，即可以得到状态和协态变量从ti时刻到ti+τ的状态响应表达式：

S(ti+τ)=Φ(τ)S(ti)+

(30)

(31)

其中：

(32)

(33)

首先，式(32)表示的状态转移矩阵只与时间有关，由式(3)、式(11)及式(30)的形式可知，协态变量初始值完全决定了协态变量的时间历程，由式(31)可知，状态的时间历程由状态初始值和积分项决定，而积分项又与协态变量的时间历程相关，故而，协态变量的初始值完全决定了协态变量和状态变量的时间历程，所以将终端约束方程转化为协态变量初值的方程组，利用具有6个未知数的高阶方程来求解协态变量初值。鉴于现在数值算法已十分成熟，这种非线性求根问题具有很好的适应性与鲁棒性，能够稳定地计算出协态变量初值，进而得到最优轨迹。

为了开始迭代算法，需要给出协态变量初值的初始猜想，对于间接法而言初始猜测值直接影响到算法的收敛。火箭上升段轨迹优化一般采用真空条件下的解作为初始猜想，具体的求解方法见文献[7]，在得到初始猜想值后，通过同伦法逐步增加大气密度直到获得100%真实大气环境下的最优轨迹。

3 仿真分析

为了验证轨迹优化方法的实用性和鲁棒性，取表1中三种不同上升情况进行了仿真分析。仿真的初始条件为：高度1310m，速度84m/s，弹道倾角82°，并采用同一组起始值。

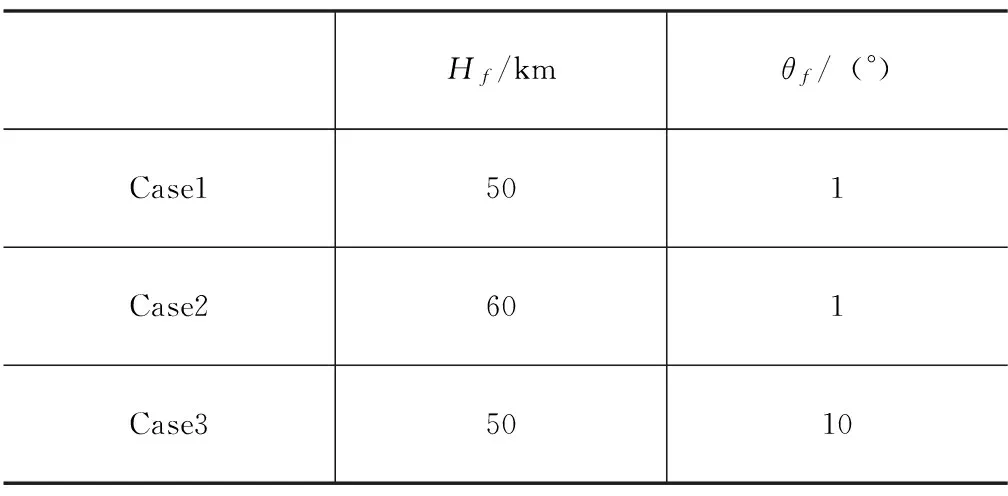
表1 仿真算例终端约束Tab.1 Terminal constraints for simulation

通过图2～图4的仿真结果可以看出，算法针对三种不同的终端约束，均可由同一组起始值得到最终结果，同时求得的最优轨迹状态量变化合理，能够精确满足不同的终端和过程约束，具有良好的适应性和鲁棒性。

图2 时间-高度曲线Fig.2 Time-altitude curve

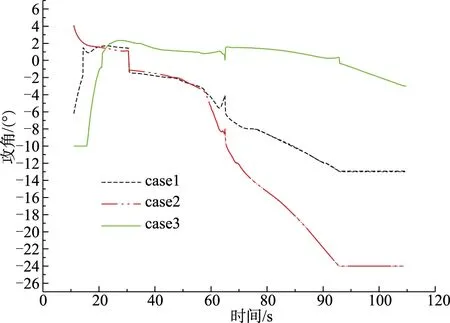
图3 时间-攻角曲线Fig.3 Time-angle of attack curve

图4 时间-弹道倾角曲线Fig.4 Time-flight path angle curve

4 结论

本文针对固体火箭飞行器上升段轨迹优化问题设计了一种基于间接法的迭代求解方法，通过本文的研究可以看出：

1)对于不同的终端和过程约束，最优算法均可以稳定地得到最优轨迹，具有较强的适应性和鲁棒性。

2)本文采用的基于状态响应方程的迭代方法，通过拟牛顿法进行数值求解，可以较快地得出最优轨迹，并且能够保证收敛性，可以进一步为在线最优闭环制导方法提供基础。

[1] Ping Lu，HongSheng Sun，Bruce Tsai.Closed-loop endo-atmospheric ascent guidance[J].AIAA 2002-4558:1-17.

[2] Ping Lu，Lijun Zhang，Hongsheng Sun.Ascent guidance for responsive launch a fixed point approach[J].AIAA 2005-6453，2005.

[3] PingLu，Binfeng Pan.Highly constrained optimal launch ascent guidance[J].Journal of Guidance，Control，and Dynamics. 2010，33(2):404-414.

[4] 宣颖，张为华，张育林.基于Legendre伪谱法的固体运载火箭轨迹优化研究[J].固体火箭技术，2008，31(5):425-429.

[5] 宗群，田伯苓，窦立谦.基于Gauss伪谱法的临近空间飞行器上升段轨迹优化[J].宇航学报，2010，31(7):1775-1781.

[6] Dukeman G A.Atmospheric ascent guidance for rochet-powered launch vehicles[R].AIAA 2002-4559.

[7] Calise A J，Nahum Melamed，Seungjae Lee.Design and evaluation of a three-dimensional optimal ascent guidance algorithm[J].Journal of Guidance，Control，and Dynamics，1998，21(6):867-875.

Indirect Method-based Ascent Trajectory Optimization

WU Jia-liang

(Beijing Electromechanical Engineering Research Institute，Beijing 100074，China)

Ascent trajectory optimization of solid rockets is important for engineering.Aiming at this problem，a feasible approach is proposed to obtain optimal ascent trajectory.Based on zero sideslip assumption to construct model，the direction of body longitudinal axis is chosen as control input.The minimum principle is used for optimization.Using indirect method，the vacuum solution is taken as initial guess，and based on state response to construct an iteration approach.With the path constraint of attack of angle，the optimal trajectory is gotten through homotopy algorithm.The results indicate that this method converges steadily and robustly.

Solid rockets；Ascent；Optimal control；Trajectory optimization；Indirect method

2015-03-26；

2015-05-18。

吴嘉梁(1989-)，男，工程师，主要从事导航制导与控制方面的研究工作。

V412.1

A

2095-8110(2016)02-0014-06