参考阵元可自适应调整的阵列天线抗干扰方法

陈耀辉，刘 鹏，徐振兴，汤丁诚，董启甲，王 盾

(中国空间技术研究院航天恒星科技有限公司，北京100086)

参考阵元可自适应调整的阵列天线抗干扰方法

陈耀辉，刘 鹏，徐振兴，汤丁诚，董启甲，王 盾

(中国空间技术研究院航天恒星科技有限公司，北京100086)

针对导航接收机抗干扰阵列天线在某些干扰来向存在抗干扰效果减弱的问题，建立了基于功率倒置算法的阵列信号处理模型，提出一种参考阵元可自适应调整的阵列天线抗干扰方法。以四阵元均匀圆阵为例进行了仿真验证，仿真结果表明，相比于参考阵元固定的功率倒置算法，此方法能够很好地解决部分干扰来向抗干扰效果减弱的问题。

阵列天线；功率倒置；参考阵元；自适应；抗干扰

0 引言

卫星导航系统由于能为全球陆、海、空、天的各类军民载体提供全天候连续高精度的三维位置、速度和精密时间信息，已经成为人类从事政治、科学、经济和军事活动中必不可少的工具[1]。目前的导航定位系统主要有美国的GPS、俄罗斯的GLONASS、欧洲的GALILEO系统和我国的BDS[2]。然而，由于目前复杂的电磁干扰环境，卫星导航系统本身存在的一些问题也逐渐暴露出来，比如由于国际电信联盟(International Telecommunication Union，ITU)对地面接收不同频段卫星信号功率密度的限制，致使地面接收到的卫星导航信号相当微弱(如GPS L1 C/A码卫星信号最小功率约为-158.5dBW，比接收机热噪声还要弱20～30dB)[3]，很容易受到各种类型射频干扰的影响。因此，需要引入干扰抑制技术来提高卫星导航接收机的抗干扰能力。鉴于当干扰和有用信号频率相同时，时域和频域抗干扰技术在对干扰抑制的同时，也会抑制有用信号，所以可以根据干扰和有用信号的空间来向不同，在空域对干扰进行抑制，保证有用信号正常接收，因此阵列天线抗干扰技术[4]得到了广泛的应用。

阵列天线抗干扰技术常用的包括波束形成[5]和自适应调零算法[6]，自适应调零算法由于不需要知道期望信号和干扰噪声的相关信息，而获得了广泛的应用，这其中最常用的是基于最小噪声方差(Minimum Noise Variance，MNV)准则[7]的功率倒置算法。功率倒置算法通过在强干扰信号方向形成零陷来提高信干噪比，并且干扰越强形成的零陷越深。针对功率倒置算法的研究国外开展的很早，早在20世纪70年代，Compton[8]就对功率倒置自适应阵列的概念和性能做了研究。由于导航卫星信号非常微弱，比接收机热噪声还要弱20～30dB，所以卫星信号几乎不受影响，并且功率倒置算法不需要知道导航卫星信号以及干扰的相关信息，因此在卫星导航接收机中获得了广泛的应用。国内关于功率倒置算法在卫星导航接收机中的应用的文献也有很多[9-12]，但是现有的功率倒置算法均为参考阵元选取固定，即约束导向矢量固定的情况。然而在实际应用过程中，这种参考阵元固定的情况会导致部分干扰来向抗干扰效果减弱的问题。文献[13]指出，与干扰信号来向在天线口面的投影垂直的阵元连线上的所有阵元等同于1个有效阵元，使得这个方向对消干扰个数小于M-1(业内普遍接受的观点是：包含M个阵元的天线阵列能够消除的最大干扰数为M-1个)。本文在研究过程中发现，在功率倒置算法中，当干扰信号来向在天线口面的投影垂直于某2个阵元(均非参考阵元)连线时，该方向的抗干扰效果减弱，具体表现为该方向可抑制的最大干扰个数小于M-1；当干扰信号来向在天线口面的投影垂直于参考阵元和另外某个阵元连线时，该方向的抗干扰效果很好，具体表现为该方向可抑制的最大干扰个数大于M-1。

针对目前阵列天线抗干扰技术中存在的部分干扰来向抗干扰效果减弱的问题，本文首先建立了功率倒置算法的阵列信号处理模型，提出了一种参考阵元可自适应调整的阵列天线抗干扰方法，并以四阵元均匀圆阵为例进行了仿真验证，仿真结果表明，相比于参考阵元固定的功率倒置算法，此方法能够很好地解决部分干扰来向抗干扰效果减弱的问题。

1 均匀圆阵信号模型

首先介绍一下本文采用的均匀圆阵的信号模型。

图1所示为均匀圆阵，M个阵元位于同一平面内，编号为1～M的阵元均匀分布于半径为R的圆周上，以圆心为坐标原点，圆心与阵元1的连线为X轴，阵元平面法向为Z轴，采用右手坐标系。俯仰角θ为入射信号方向与法线的夹角，方位角φ为入射信号与原点的连线在X-Y平面的投影与X轴的夹角。

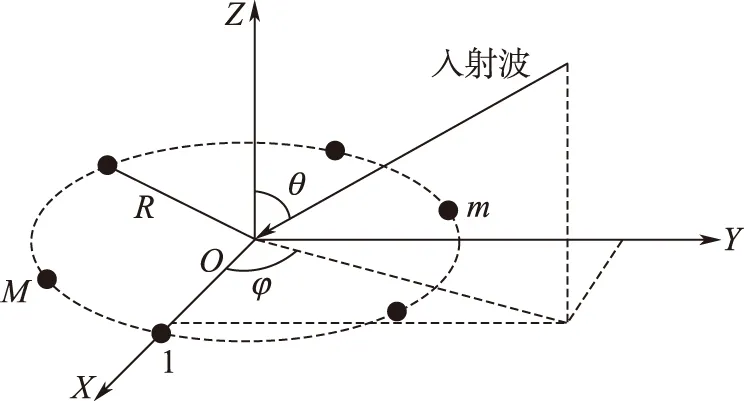
图1 均匀圆阵Fig.1 The uniform circular array

在某个时间，原点和第m个阵元接收到的信号的相位差为

m=1,2,…,M

(1)

则阵列导向矢量可以表示为

(2)

2 现有功率倒置算法

功率倒置算法是基于最小噪声方差准则，也称为线性约束最小方差(Linearly Constrained Minimum Variance，LCMV)准则[14]建立的，也就是将自适应阵列的输出功率最小作为最佳化准则。LCMV准则用公式表示为：

(3)

为了避免因使用输出功率最小原则而导致计算出的权矢量W=0，因此现有的功率倒置算法中通常规定WHs=1，s=[1,0,…,0]T，该约束条件可以理解为保持通道1接收到的数据为单位增益，通过自适应调整其他通道的加权系数，使输出信号功率最小。针对不同的天线阵形约束导向矢量s中1的位置可能会不同，也就是参考通道的选取会有所不同，例如在文献[15]中将参考通道选为线阵中心阵元对应的通道。但是无论什么阵形，参考阵通道总是固定不变的，即约束导向矢量s固定，这里假定为s0。功率倒置阵列天线抗干扰处理系统框图如图2所示。

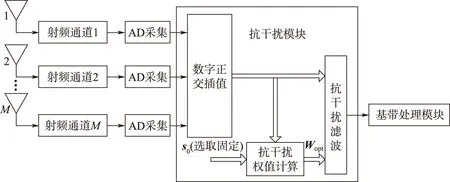
图2 现有的功率倒置阵列天线抗干扰处理系统框图Fig.2 The block diagram of the existing power inversion anti-jamming processing system

假设阵列天线为M阵元，每个天线阵元接收到的信号经过射频模块、AD采样以及数字正交插值处理后输出为xm,m=1,2,…,M，矢量形式可以表示为

X=[x1,x2,…,xM]T

(4)

通常阵列天线接收的信号包括卫星信号、干扰信号和噪声，令xsm，xJm，xnm，m=1,2,…,M分别表示每个阵元接收到的卫星信号、干扰信号和噪声。矢量形式可以分别表示为：

XS=[xs1,xs2,…,xsM]T

(5)

XJ=[xJ1,xJ2,…,xJM]T

(6)

Xn=[xn1,xn2,…,xnM]T

(7)

则阵列接收的信号的矢量形式还可以表示为

X=XS+XJ+Xn

(8)

自适应权矢量可以表示为

W=[w1,w2,…,wM]T

(9)

经过加权后的阵列输出可以表示为

Y=WHX

(10)

假定卫星信号、干扰信号和每个通道的噪声信号均互不相关，各通道噪声为独立的空间白噪声，且功率相同。

阵列输出功率Pout可以表示为

(11)

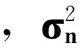
构造拉格朗日函数

L(W)=WHRXW+λ(WHs-1)

(12)

取式(12)的梯度，并令

▽WL(W)=0

(13)

从而可以求得自适应权矢量为

(14)

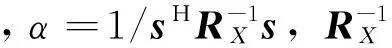
3 改进功率倒置算法

针对现有的功率倒置算法参考阵元固定，导致部分角度抗干扰效果减弱的问题，提出了一种改进方法，即参考阵元可自适应调整的方法。当干扰信号来向在天线口面的投影垂直于某2个阵元(均非参考阵元)连线时，这2个阵元接收到的干扰信号相同，所以这2个通道数据之间的相关性最大，如果此时可以将参考阵元调整为这2个阵元中的某一个，就可以大大改善该方向的抗干扰效果。本文的改进算法正是基于这种想法提出的，图3给出了改进的功率倒置阵列天线抗干扰处理系统框图。

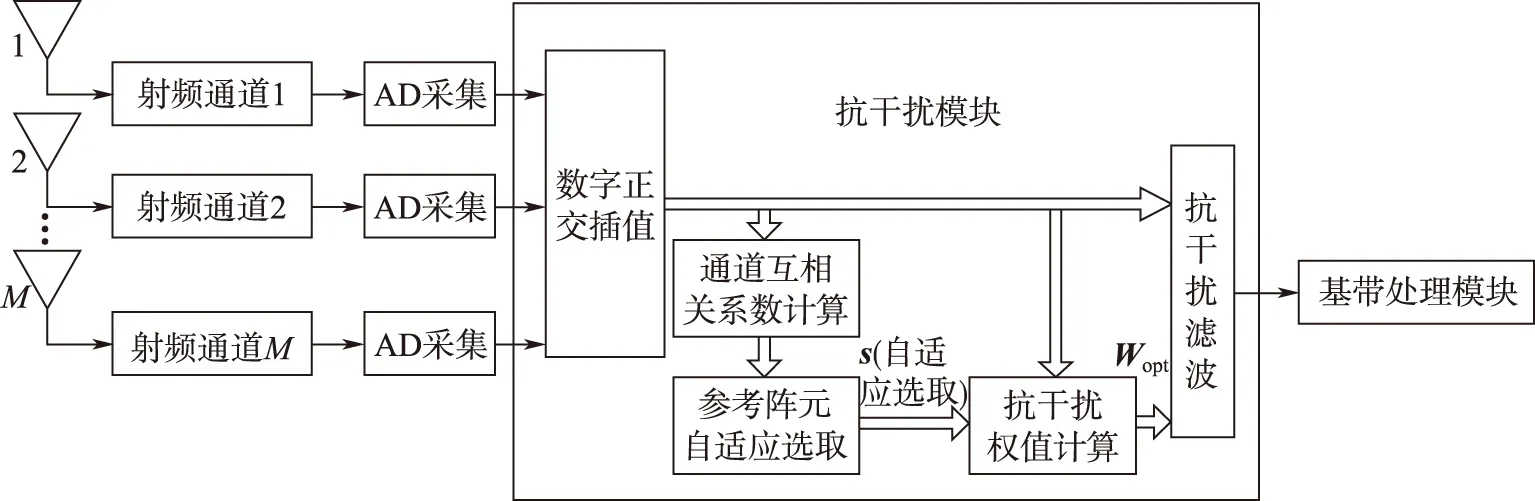
图3 改进的功率倒置阵列天线抗干扰处理系统框图Fig.3 The block diagram of the improved power inversion anti-jamming processing system

与现有的功率倒置算法不同的是，这里的参考阵元是根据一定的准则自适应调整的，参考阵元的改变表现为约束导向矢量s中1的位置的改变。

这里首先给出通道相关系数的定义，通道m接收到的信号功率表示为

(15)

则通道m和通道n的通道相关系数可表示为

(16)

其中，当m=n时，ρmm为通道m的自相关系数；当m≠n时，ρmn为通道m和通道n的互相关系数。

具体的实施过程就是：利用阵列天线接收并经射频模块、AD采样以及数字正交插值处理后的每个通道一定长度的数字复信号数据，分别计算每个通道数据与其他任一通道数据的互相关系数，然后选取通道互相关系数模值最大的两个通道作为备选通道，然后再从备选通道的取模的互相关系数中选出次大值，将次大值和最大值均包含的通道选为参考通道，根据参考通道调整约束导向矢量，最后根据选取的约束导向矢量计算抗干扰滤波权值，进行抗干扰滤波处理，输出抗干扰处理后的数据。

4 仿真验证

为了验证改进算法的有效性，这里以四阵元均匀圆阵为例，对现有的功率倒置算法和改进的功率倒置算法进行仿真对比实验。对四阵元均匀圆阵的0°～360°方位角间隔15°进行仿真，并且在每个方位角分别施加1～4个点频干扰，其中4个干扰的方位角相同，俯仰角分别为85°、65°、45°和25°。

评价指标选用输出干噪比的改善情况，定义输出干噪比改善为

INRimprove=INRin-INRout

(17)

其中，INRin为输入干噪比，INRout为输出干噪比。

实际上评价指标有很多，比如输出干信比、输出干噪比、信号捕获图等，这里之所以选用干噪比改善而不选用干信比或者信号捕获图，主要是因为有用信号与干扰的入射角度不同，抗干扰处理后对有用信号的影响不同，所以干信比和信号捕获图不适合作为评价指标。

下面分别对现有的功率倒置算法(约束导向矢量为s=[1;0;0;0])和改进的功率倒置算法以四阵元均匀圆阵为例进行仿真分析。

4.1 现有的功率倒置算法

现有的功率倒置算法通常选定约束导向矢量为s=[1;0;0;0]，即固定阵元1为参考阵元。图4给出了现有的功率倒置算法的输出干噪比改善情况。

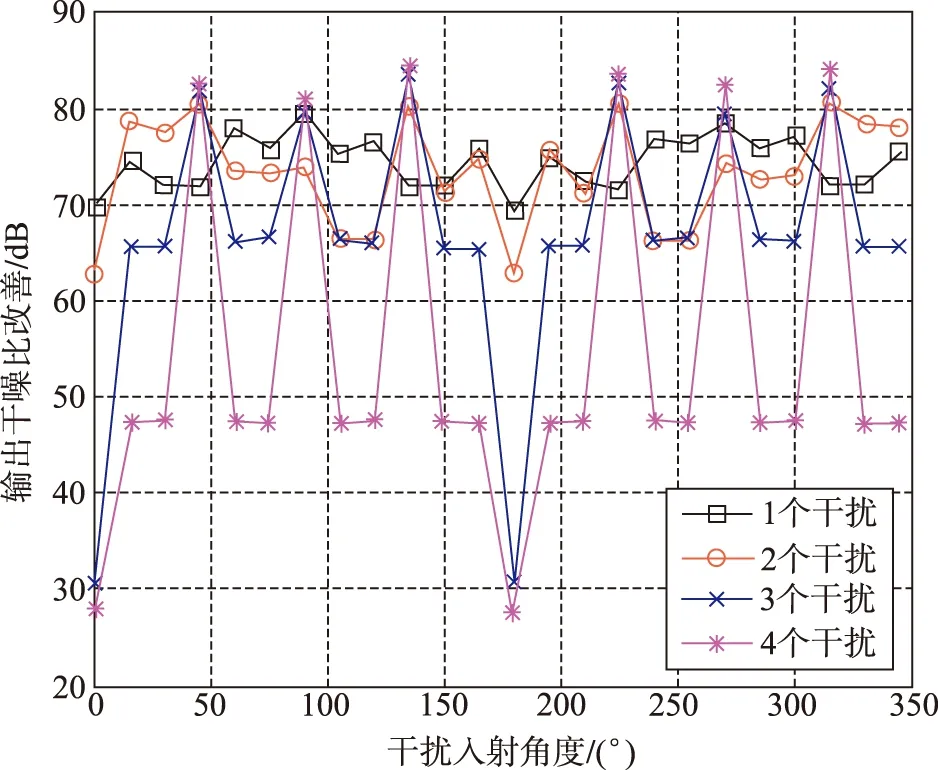
图4 现有功率倒置算法的输出干噪比改善Fig.4 The improvement of the output INR of the existing power inversion algorithm

从图4可以直观地看出在45°、90°、135°、225°、270°、315°可以抑制多于3个的干扰，在0°和180°只能抑制2个干扰，而在其他角度基本可以抑制3个干扰。

图4的仿真结果也可以用图5更直观的表示，规定阵元1(参考阵元)和圆心连线为0°，角度按逆时针方向增加。可见在0°和180°，由于阵元2和阵元4接收到的数据相同，所以这两个方向的抗干扰效果差，可以抑制的干扰个数为2个，在45°、90°、135°、225°、270°、315°均存在某个阵元与参考阵元接收到的数据相同，所以这些角度的抗干扰效果好，可以抑制的干扰个数大于3，其他角度可以抑制的干扰个数为3个。

图5 四阵元均匀圆阵不同方位角抑制干扰个数Fig.5 The number of interferences of a uniform circular array with four elements can cope with

4.2 改进的功率倒置算法

改进的功率倒置算法，即根据通道相关性，自适应地调整参考阵元。图6给出了采用改进算法的四阵元均匀圆阵不同干扰入射角度的输出干噪比改善情况。

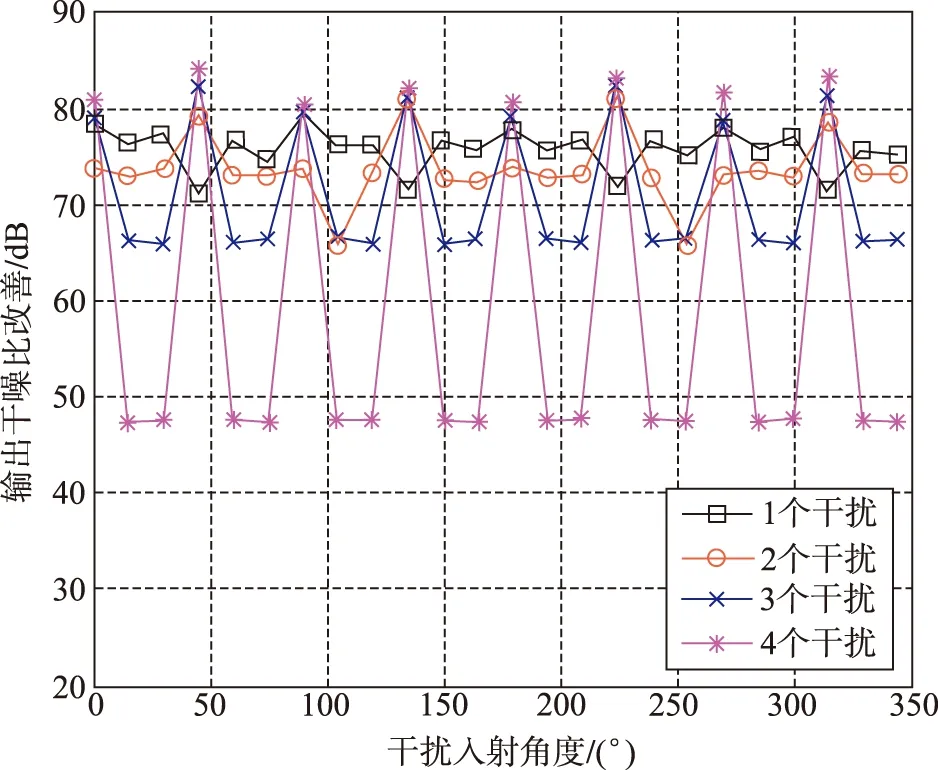
图6 改进功率倒置算法的输出干噪比改善Fig.6 The improvement of the output INR of the improved power inversion algorithm

从图6可以清楚地看出，与现有功率倒置算法相比，每个角度都至少可以抑制3个干扰，0°和180°甚至从原来只能抑制2个干扰，改善为可以抑制多于3个干扰，改善效果非常明显。

为了更清楚地对比改进前后的功率倒置算法的性能，图7给出了针对施加不同干扰个数时两种算法的抗干扰性能对比情况。

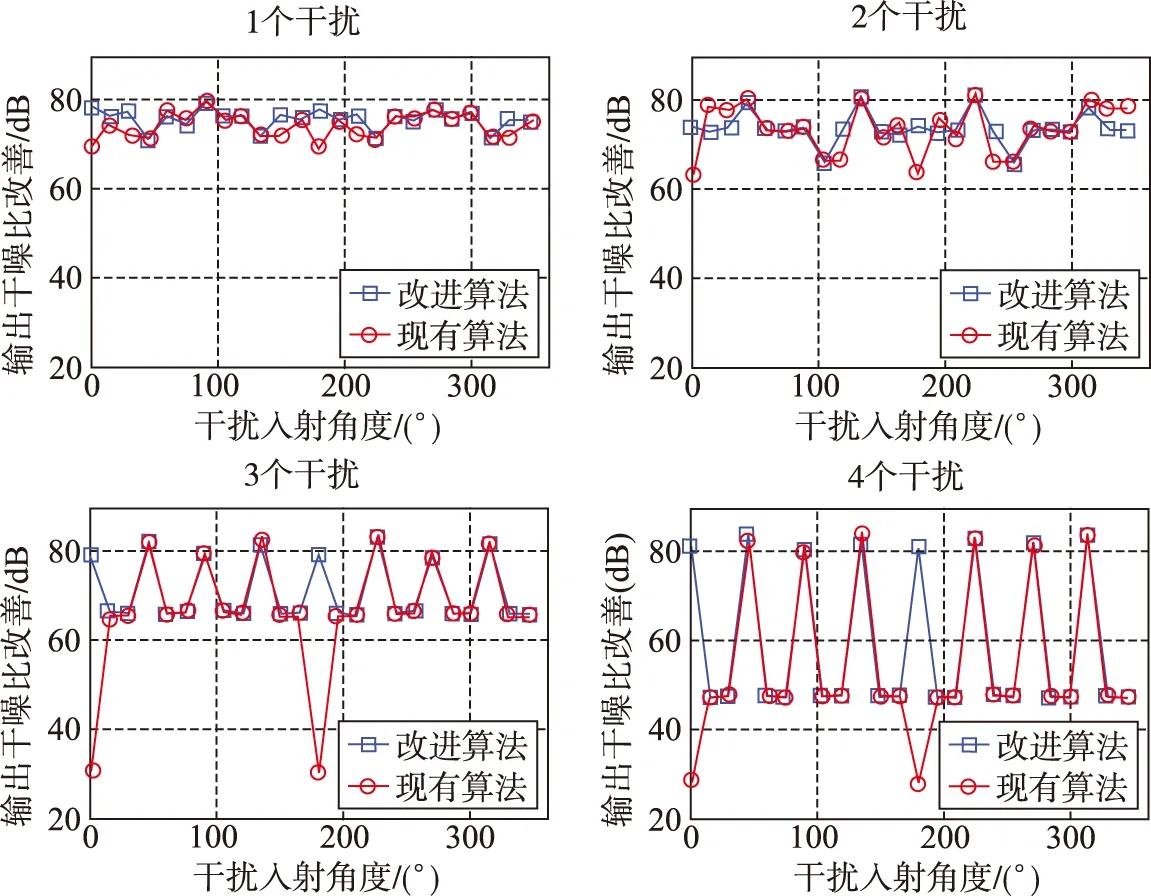
图7 改进前后的功率倒置算法的性能对比Fig.7 Performance comparison of the power inversion algorithm before and after improving

从图7可以清楚地看出，对于施加1个干扰和2个干扰的情况，两种算法性能相差无几，因为此时每个角度都能抑制2个干扰，所以改进算法的优势没有体现出来。对于施加3个干扰和4个干扰的情况，改进算法优势明显。现有功率倒置算法由于0°和180°存在有效阵元数下降的情况，所以最多只能抑制2个干扰，改进算法通过调整参考阵元，很好地解决了有效阵元数下降导致的抗干扰个数下降的问题，使0°和180°从只能抑制2个干扰改善为可以抑制多于3个干扰的情况，干扰抑制能力明显增强，且对其他角度的抗干扰效果几乎没有影响，可见相对于现有的功率倒置算法，改进后的算法优势明显。

5 结论

针对阵列天线抗干扰技术中存在的部分干扰来向抗干扰效果减弱的问题，建立了基于功率倒置算法的阵列信号处理模型，提出一种参考阵元可自适应调整的阵列天线抗干扰方法。本文以四阵元均匀圆阵为例进行了仿真验证，结果表明，相比于参考阵元固定的功率倒置算法，此方法能够很好地解决部分干扰来向抗干扰效果减弱的问题。

[1] 于国强，邱致和.导航与定位：现代战争的北斗星[M].北京：国防工业出版社，2000.

[2] 张晓明.GNSS抗干扰阵列天线的设计与实现[D].西安：西安电子科技大学，2010.

[3] Elliott D.Kaplan,Christopher J.Hegarty.GPS原理与应用[M].寇艳红，译.北京：电子工业出版社，2012.

[4] Yimin Zhang,Hao Yuan,Kazuhiro Hirasawa.Adaptive array performance in the presence of spatially spreaded onterference signals[C].Antennas and Propagation Society International Symposium,1997,1048-1051.

[5] Veen B D Van,Buckley K M.Beamforming：A versatile approach to spatial filtering[J].IEEE ASSP Magazine,1988,5(2)：4-24.

[6] Zoltowski M D,Gecan A S.Advanced adaptive null steering concepts for GPS[C].Military Communications Conference,1995,1214-1218.

[7] 王永良，丁前军，李荣锋.自适应阵列处理[M].北京：清华大学出版社，2009.

[8] R.T.Compton,JR.The power-inversion adaptive array：Concept and performance[J].IEEE Trans.on AES,1979,15(6)：803-814.

[9] 冯起，朱畅，袁乃昌.GPS接收机抗干扰自适应天线的设计[J].系统工程与电子技术，2009,31(7):1556-1559.

[10] 何永前，李建璜.GPS抗干扰接收机自适应天线阵功率倒置算法研究[J].舰船电子工程，2012,32(6)：61-62.

[11] D Meng，Z Feng，M Lu.Anti-jamming with adaptive arrays utilizing power inversion algorithm[J].Tsinghua Science Technology,2008,13(6)：796-799.

[12] Q Zhang,P Wu,S Chen.Design of anti-jamming antenna for the GPS receiver[C].Electronic Measurement and Instruments,2007,204-208.

[13] 董娟娟.多阵元天线GPS接收机抗干扰技术的研究[D]. 西安：西安电子科技大学，2013.

[14] Frost O L.An algorithm for linearly constrained adaptive array processing[J].Proceedings of the IEEE,1972,60(8)：926-935.

[15] Inder J.Gupta,Thomas D.Moore.Space-Frequency Adaptive Processing(SFAP)for radio frequency interference mitigation in spread-spectrum receivers[J].IEEE Transactions on Antennas and Propagation,2004,52(6)：1611-1616.

Anti-jamming Method of Array Antenna with Adaptive Reference Element

CHEN Yao-hui,LIU Peng,XU Zhen-xing,TANG Ding-cheng,DONG Qi-jia,WANG Dun

(Space Star Technology Co.Ltd.,China’s Academy of Space Technology,Beijing 100086,China)

This paper focuses on the issue that the anti-jamming performance of array antenna of navigation receivers is degraded when interferences come from some specific incident angles.In this paper,a signal processing model for analyzing the phenomena is established based on the Power-Inversion algorithm.An anti-jamming method of array antenna with adaptive reference element is proposed.Simulation evaluation is carried out with a model of uniform circular array of four elements and its result shows that compared with traditional method of Power-Inversion algorithm,the proposed method can well solve the problem of performance degradation which happed with some specific incident angles of interferences.

Array antenna；Power-Inversion；Reference element；Adaptive；Anti-jamming

2015-12-12；

2015-01-10。

陈耀辉(1990-)，男，硕士，主要从事阵列信号处理方面的研究。E-mail:Chen_yaohui10@163.com

TN97

A

2095-8110(2016)02-0042-06